Spark 并行化改進的SDKB-DBSCAN 聚類算法
2021-07-09 17:19:22史愛武尹杰范平
現代計算機 2021年14期
史愛武，尹杰，范平
（1.武漢紡織大學數學與計算機學院，武漢 430000；2.湖北科技學院計算機科學與技術學院，咸寧 437000）
0 引言
數據采集存儲技術快速發展積累了大量數據，對數據深入分析并指導實踐成為迫切需要，基于此大數據研究成為近年來研究熱點。聚類分析是數據挖掘中的分支，來源于多研究領域，包括統計學、機器學習、模式識別等。其可以輔助分類研究，應用在生物學、地理信息學、商業分析、互聯網搜索等領域。DBSCAN 算法是基于密度的聚類算法，它具備抗噪聲能力，能夠在具有噪聲的數據集中發現任意形狀類簇，有較好的聚類效果[1]。但DBSCAN 算法依然存在缺陷：算法在聚類中迭代計算，需要大規模內存磁盤I/O 交互，降低了計算速率；算法需要人工干預確定閾值，且對初始參數大小有敏感性，參數選定不準確，易降低聚類準確率；對不同數據集分布，特別是密度分布不均勻的樣本集，采用全局閾值，對樣本核心點，邊界點和噪聲點的劃分會存在偏差，降低聚類準確率；對分布分散程度不高的數據集，全局閾值會造成不同簇類合并成同一簇類，降低聚類準確率。針對以上問題，許多學者對DBSCAN 算法進行研究及改進。
周水庚等人[2]提出矩形分區局部聚類策略；邱寧佳等人[3]提出基于MapReduce 的GA-DBSCAN 算法，胡贏雙等人[4]提出基于MapReduce 網格劃分強連通聚類算法；黃明吉等人[5]提出樣本數據量劃分策略和Spark并行化，計算速率有所提升，但存在網格劃分，數據量劃分等方法不能相對較高契合多密度不均勻聚類，準確率有所下降。韓利釗等[6]提出網格合并方法，可靈活定位不均勻數據劃分區域，但其需要確定Eps參數初值，且算法時間復雜度相對較高，效率相對較低；于亞飛等人[7]、宋金玉等人[8]提出DBSCAN 算法參數配置策略，利用距離k-dist矩陣以及概率密度分布曲線獲取參數值，提高參數自適應性，但是該方法需要人工干預確定k值，不同k值對應擬合曲線導數計算的大小不同；宋明等人[9]提出數據交替分區增量計算，田路強[10]提出分布式增量聚類，在提高聚類準確率同時會出現數據增量合并效率偏低。
針對上述學者研究需要提升的方面，提出SDKBDBSCAN 聚類改進算法，設計不規則動態區域并行計算模型，采取過濾不規則邊界單元區域，指定不重疊區域的合并策略，應用概率密度以及均值方法，搭建Spark 并行計算框架算法架構。
1 基本理論內容
1.1 DBSCAN算法
DBSCAN 算法基于密度對空間樣本形成類簇。在n維空間內，以參數設定閾值半徑Eps以及閾值大小為聚類限定條件，將空間內樣本點以迭代計算方式發現任意形狀類簇，過濾樣本數據集噪聲點，得到密度聚類結果。在n維樣本集中，列出算法相應定義：
定義1Eps鄰域在n維空間內對任意的樣本點p，以p為中心，Eps為半徑內所有樣本點集合。即表示為式（1）：
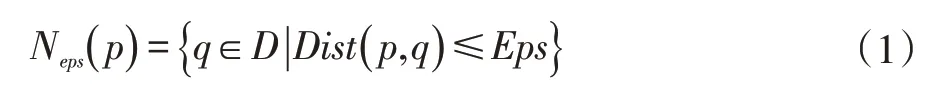
其中Dist(p,q)表示p到q的距離，通常情況下，用Minkowski距離公式計算Dist，公式表示為式（2）：
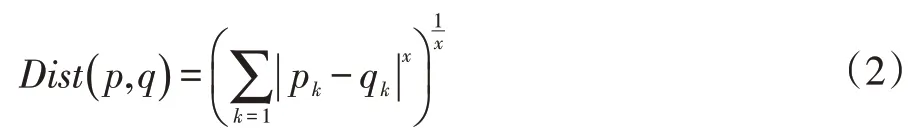
定義2核心點在n維空間內對任意樣本點p，滿足在以p為中心點的鄰域值不少于Minpts個樣本點。即表示為：，稱p為核心點；
定義3邊界點在n維空間內存在一個p不屬于核心點，而且該點落在核心點的鄰域范圍內，稱p點為邊界點；
定義4噪聲點在n維空間存在一個點p不屬于核心點，而且該點落在所有核心點的鄰域范圍之外，稱p點為噪聲點；
定義5直接密度可達在n維空間內，若存在p在q的Eps鄰域范圍內，并且q為核心點，可稱p是從q出發直接密度可達，不具有對稱性。
定義6密度可達 在n維空間內，若存在數據集，滿足從pi出發到pi+1直接密度可達，那么可以說是p1出發到pi+1是密度可達。不具有對稱性但具有傳遞性。
定義7密度相連在n維空間內，若存在o，從點o出發到p密度可達，且從o出發到q密度可達，可稱p和q密度相連。具有對稱性，且p和q可以不屬于核心點。
1.2 Spark并行內存計算框架
Apache Spark 是加州大學伯克利分校的AMP Lab實驗室研究并開發，發展為Apache 頂級項目。Spark 是內存分布式計算引擎框架，在沿用MapReduce 計算引擎結構基礎上，引入RDD（Resilient Distributed Dataset）分布式彈性數據集。執行時數據映射到RDD 結構中，發揮其內存計算結構特性以及在迭代計算中將數據反復緩存至內存的特點，與MapReduce 將數據在內存與硬盤I/O 轉換相較，提高十倍甚至百倍的計算速度[11]。
從RDD 依賴關系中，可對RDD 的操作分為邏輯傳遞的轉換操作和實際運行的行動操作，轉換操作不會立即執行，要等行動操作全觸發。用于并行操作重要的算子，包括Map、Reduce、Join、Foreach 等，對算法優化起到關鍵作用。
Spark 整體架構如圖1 所示。
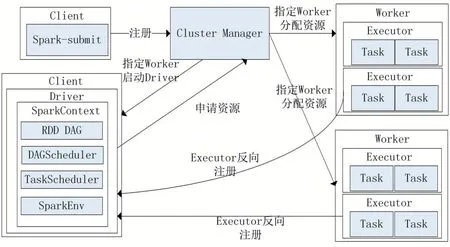
圖1 Spark架構圖
2 SDKB-DBSCAN改進算法
2.1 不規則動態密度區域劃分
網格劃分即設存在一個d維數據集S={s1,s2,…,sd}，S中各維數據表示為在第i維數據區間[ri,li)上i=1,2,..,d且各數據是有界的，則稱D=[r1,l1)×[r2,l2)×…×[rd,ld)為d維的數據空間。D維空間是不相交數據集，表示為數據各個屬性，對每一維數據空間劃分，可形成d維網格單元，網格單元是以左閉右開的形式表示，其是d維空間基本劃分單元[9]。對于網格劃分，給出d維空間下每一維數據空間網格寬度的計算公式，表示為式（3）：
其中c為擴充線性方程，適當放縮網格寬度，找到合適的初始單元網格。計算各個維度的邊界差與樣本個數的比并取其最小值作為網格寬度的基準。之后可確定各個數據維度網格數量并確定其網格索引[12]。表示為式（4）：
區域合并即初始網格單元后，在d維空間內數據p是包含在某一個網格單元中，每一個網格單元由不同數據填充，可用每一個不相交的網格數據個數作為網格單元密度，den(f)表示密度大小。不規則分區算法偽代碼如下所示：
算法1 貪心策略廣度優先搜索層次歸并算法
輸入：DataSet 數據集
輸出：partitionInfo 分區數據集
區域劃分是控制相鄰單元網格密度相對差比來合并網格單元，引入貪心策略，將問題分解成若干子問題，尋找未標記索引對應的密度最大值為核心網格單元，與相鄰網格單元計算密度相對差比[13]表示為式（5）：
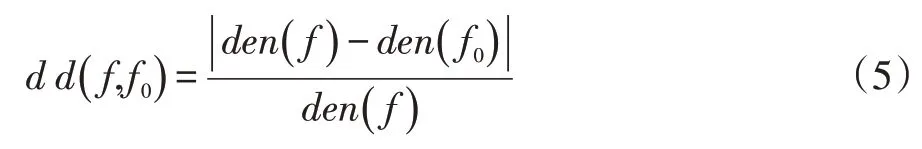
將其作為判斷網格合并條件，初始核心與相鄰網格依次按上式計算，并將滿足d d()f,f0<ε條件，來確定相鄰網格歸屬。若滿足條件時，將相鄰網格與核心網格標為一類，為減弱平均密度帶來的密度差比波動，采取一種層次歸并算法，統一平均密度值，其表示為式（6）：
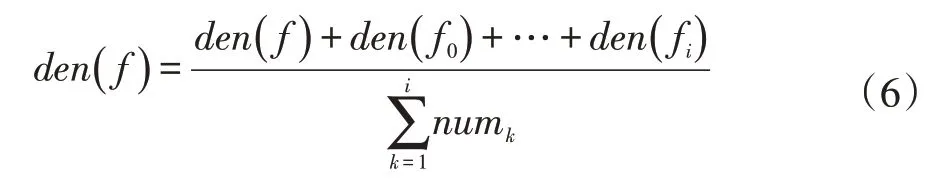
區域劃分采用廣度優先搜索算法，不斷合并滿足條件的網格；不滿足條件時，相鄰單元網格標記為邊界網格。將所有計算過的網格標記為已搜索狀態，直到本次合并結束。若此時還有符合條件是未搜索狀態，則繼續求解子問題，直至區域劃分結束。
2.2 區域自適應參數局部聚類
數據區域劃分后，將不同區域數據分配到Spark 的RDD不同分區中。改進算法優化不同分區自適應確定Eps和Minpts，一定程度減小密度不均勻數據所統一參數對聚類的影響。
改進算法在自適應確定參數上引入核密度估計理論。定義為：設X1,X2,…,Xn是從總體X中抽取的獨立同分布樣本，總體X有未知分布密度函數f(x),x∈R，則f(x)的核密度估計為式（7）：
式中函數K(u)為核函數，h是與n有關的正數，為光滑參數或者窗寬[14]。
設定不同h窗寬，可得到不同效果f(x)。h窗寬過小時，f(x)限制局部觀測數據，會得到過多錯誤峰值，估計函數效果不理想，將h映射對應自適應Eps取值過小，會增加樣本成為噪聲概率，降低聚類準確率；h窗寬過大時，f(x)過于光滑，無法去反映出正確的密度函數，同樣h窗寬對應Eps取值過大，對于不同密度數據會錯誤合并為同一類，降低聚類準確率。
h窗寬的確定可影響Eps確定，改進算法采用Gaussian做為核函數，最小化積分均方誤差MISE計算求得最優h窗寬，獲取最優Eps[15]。MISE表示為式（8）：
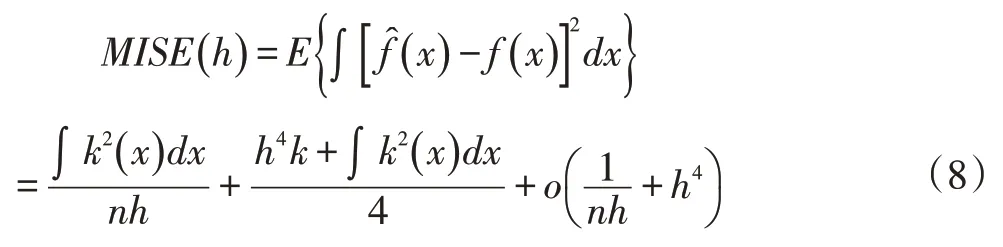
其中可將AMISE(h)表示為漸進積分均方差誤差，表示為式（9）：
求解最優h窗寬，即需要AMISE(h)誤差值取得最小，因此對上式求偏導數可得式（10）：
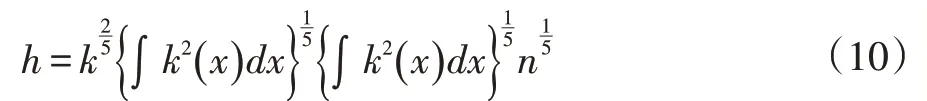
數據樣本總體服從方差為σ2的正態分布，用高斯核函數，代入式（10）可得式（11）：
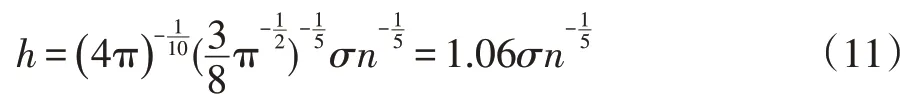
由此可得自適應下最優Eps。
自適應確定Minpts采用在分區中每個Eps鄰域范圍內樣本個數的均值策略，表示為式（12）：
其中Num即表示在每個Eps鄰域范圍內所包含樣本數量，將上式定義到并行結構中內存計算。
2.3 自定義聚類合并策略
區域劃分以及分區自適應確定參數并行計算后，給出自定義策略將局部聚類結果合并，形成最終全局聚類[16]。改進合并策略采用對各分區下不規則邊界網格單元中樣本進行局部合并。具體分為以下幾點：
（1）設在兩個分區C1,C2的邊界網格上分別對應樣本P1,P2，若P1,P2分別在對應分區上為其自適應確定下Eps的核心點，并且存在dist(P1,P2)≤min(epsC1,epsC2)，可以判定C1,C2合并為同一分類；
（2）在一類簇不規則邊界網格單元中的噪聲點，有可能是另一個類簇中的邊界點。設在一個分區C1中存在一個噪聲點P1，若在其他類簇中如C2的邊界網格單元中樣本能符合一個P2使得dist(P2,P1) ≤epsC2，則將分區C1中的P1劃分為C2類；
（3）在兩個不規則邊界網格單元中的噪聲點，會有邊界樣本個數一側相對較少或者密度相對較低的情況。在聚類合并的全局條件下，若存在兩個分區C1,C2中分別有噪聲點數據集S1,S2，其中一個樣本P，滿足dist(P,Pi)≤min(epsC1,epsC2)的鄰域范圍內密度直達的樣本Pi有Numi≤min(epsC1,epsC2)，則可將噪聲點P定義為一個新類簇中的核心點，剩余的樣本Pi為新類簇中的邊界點。
2.4 改進算法流程結構
上述為SDKB-DBSCAN 具體改進算法方案，這里給出算法整體流程與Spark 并行化設計結構。SDKB_DBSCAN 算法執行邏輯流程如圖（2）所示。
SDKB_DBSCAN 算法Spark RDD 并行化轉換執行算子流程如圖（3）所示。
圖3 SDKB_DBSCAN RDD轉換執行算子流程圖
InitData 在經過mapValue 算子切割后，將InitRDD轉化成DataFrame 數據格式。數據在分區階段設計結構dfZone
分區內并行計算LocalDBSCAN，動態自適應確定Eps以及Minpts。分區聚類結果標記數據結構partition
改進算法分區合并策略，設計數據結構為merge
3 實驗分析
3.1 實驗環境
為驗證改進算法準確率和運行速率性能，編碼實現改進算法，設計實驗加以分析。實驗環境如表1所示。
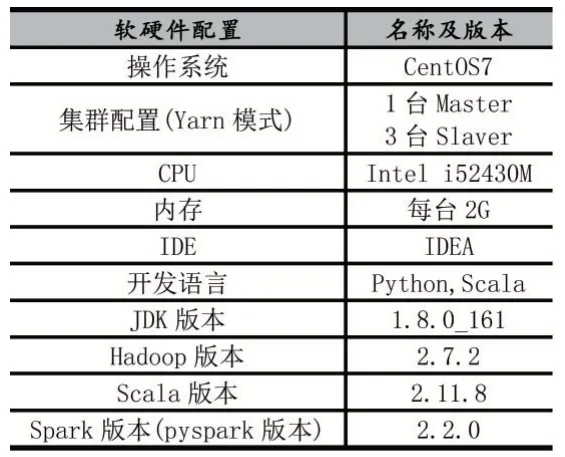
表1 實驗硬件以及軟件環境
實驗采用對串行DBSCAN 算法，并行化網格分區SparkDBSCAN 算法，以及SDKB_DBSCAN 改進算法對比實驗，使用的數據集如表2 所示。
表2 實驗數據集
實驗數據聚類結果對比分析：全局人工干預閾值Local_DBSCAN 算法，類簇劃分需多次調參以獲取更適類簇，圖4（a）所示，密度不均勻聚類存在噪聲點較多，誤差較大；Spark_DBSCAN 并行算法，網格分區并行迭代，全局人工干預閾值，重疊邊界區域局部合并來實現并實驗，聚類依賴于網格劃分，不能做到動態參數自適應，且網格分區會使算法無法在全局范圍識別任意類型簇，圖4（b）所示，SparkDBSCAN 算法聚類準確率，略低于Local_DBSCAN 算法；SDKB_DBSCAN 改進算法，不規則動態分區降低密度不均勻敏感性，動態自適應閾值減少人工干預誤差并內存計算，設計緩存機制模型，圖4（c）所示，改進算法在聚類數據尤其是密度不均勻類簇準確率較前兩種算法有相對提升。
圖4 三種算法數據聚類效果圖
Local_DBSCAN、SparkDBSCAN、SDKB_DBSCAN算法準確率量化數據如表3 所示。
表3 三種算法聚類準確度（%）
3.2 并行實驗性能
從運行數據量和時間來看，Local_DBSCAN 算法在相同數據維度下有明顯時間消耗，效率限制明顯，串行計算消耗更多CPU 與內存，SDKB_DBSCAN 改進算法，設計并行計算有向無環圖DAG 以及Spark 并行過濾緩存機制與類簇合并融合算法，從局部聚類到聚類合并提升計算效率，在數據分區階段廣度優先搜索不規則分區，需消耗一定計算資源，整體來講Spark_DBSCAN與SDKB_DBSCAN 改進算法聚類效率在數量級上相同。圖5 所示，SDKB_DBSCAN 改進算法運行效率略高于Spark_DBSCAN 算法，高于Local_DBSCAN 算法。
圖5 三種算法時間消耗對比圖
加速比是同一任務運行單核處理和并行處理運行時間消耗的比率，可以用來衡量并行性能。圖6 顯示不同核數不同數據量加速比。
圖6 SDKB_DBSCAN多核加速比
在核數低且數據量少的情況下，對并行處理效率并無明顯提升，其中調度資源分配，并行化Suffle 階段會消耗一定時間，若數量增加核數增大，則加速比提升明顯。
4 結語
針對DBSCAN 算法存在的缺陷，串行計算速度慢，人工干預確定閾值參數敏感，數據密度不均勻降低準確率等問題，提出一種不規則動態區域劃分，自適應并行確定各閾值，不規則邊界區域緩存機制合并的SD?KB_DBSCAN 聚類改進算法。實驗表明，改進算法對準確率和運行速率相對優于Local_DBSCAN 以及Spark_DBSCAN 算法。
后續工作，將圍繞對更多的數據集進行測試和算法優化。包括分區策略算法選取優化以及Spark 并行融合設計優化，改進算法運行模式，Spark 緩存策略和內存管理優化，進一步提高SDKB_DBSCAN 聚類改進算法性能。
