GeoGebra軟件在物理可視化教學中的應用

劉健智 程 婷

(湖南師范大學物理與電子科學學院，湖南 長沙 410081)

1 GeoGebra軟件與可視化教學

GeoGebra軟件可以代替傳統板書呈現一些無法板書或板書不清的復雜情境，甚至呈現3D效果，訓練學生的空間思維能力；可以呈現動態變化的過程，構建物理模型，加深學生對物理規律的理解；亦可以展示科學推理的過程，使得思維方法更加形象、具體……這些都有利于解決物理學科的抽象性問題，利用視覺思維提升學生的感性認識，增強物理教學的可視化.[1-3]

2 在平拋運動中的具體應用

平拋運動是學生在高中階段接觸的第一種曲線運動，也是后面分析帶電粒子在電磁場中運動的基礎，在高中物理體系中具有重要地位.利用GeoGebra軟件輔助平拋運動的可視化教學主要可體現在數據處理、規律推導以及臨界過程分析3個方面.

2.1 數據處理的可視化

2017年版課程標準要求“通過實驗，探究并認識平拋運動的規律”.[4]在2019新人教版高中物理教材的平拋運動實驗中，只涉及平拋運動水平和豎直方向運動規律的探究，未提及平拋運動的軌跡特點.[5]筆者利用GeoGebra軟件的擬合功能豐富數據處理，探究平拋運動的軌跡特點.

利用傳感器和計算機獲得平拋運動的水平位移和豎直位移如表1所示.[5]打開GeoGebra軟件(筆者使用的版本為GeoGebra classic 5)，在表格區輸入數據.其中，數據小數位或有效數字可通過精確度進行設置.需要說明的是，如果最后一位或幾位小數為0，系統會自動舍去，無法實現數據格式的統一，但并不影響擬合結果.

表1 傳感器獲得的平拋運動的軌跡數據

將數據創建為點列，粗略還原平拋運動的實際軌跡.猜想其為拋物線，則應滿足一元二次函數的解析方程.考慮拋出點為坐標原點，解析形式應為f(x)=ax2.利用“fit”指令將點列擬合成f(x)同樣形式的函數g(x).由于g(x)只是軟件計算出的最匹配點列的函數，因此并不是所有的點都會滿足該函數方程.從圖1可以看出，點列與二次函數圖像基本吻合，說明猜想合理.

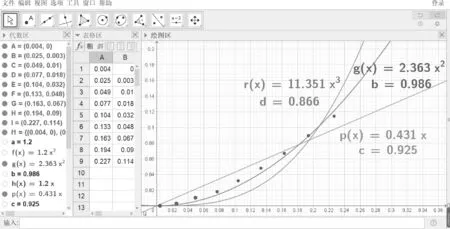
圖1 GeoGebra軟件y-x擬合函數圖像

為了進一步提高結論的可信度，利用“rsquare”指令計算點列與g(x)的相關系數為r=0.986.說明在誤差允許的范圍內，平拋運動軌跡確實是一條拋物線.用同樣的方法也能計算點列與一次函數(r=0.925)、三次函數(r=0.866)甚至其他函數的相關系數，但從數值上看只有二次函數的相關系數最高，從側面反映點列最符合二次函數關系，使學生養成嚴謹的科學態度.

在此基礎上，利用GeoGebra的代數運算功能，可直接計算初速度的大小.如果是利用頻閃照相的方式探究平拋運動規律，保證每兩個點間隔時間相同，還能實現平拋運動y-x到y-t、x-t圖像的轉化，滲透運動的合成與分解思想；若再利用多項式擬合，就能直接從y-t、x-t圖像中分析出豎直和水平方向的運動規律，十分方便.

2.2 規律推導的可視化

平拋運動有兩條重要推論，一是速度偏向角的正切值為位移偏向角正切值的兩倍，二是速度延長線一定過水平位移的中點.日常教學多是從代數關系入手講解，過于抽象枯燥.利用GeoGebra軟件，一是比黑板作圖更加規范；二是能直接顯示如水平位移中點、速度延長線與x軸交點的位置坐標，更加直觀；三是能將規律動態化，證明這兩條規律在平拋運動的任何位置都成立，趣味性更強.下面是利用GeoGebra軟件進行規律推導的具體操作.

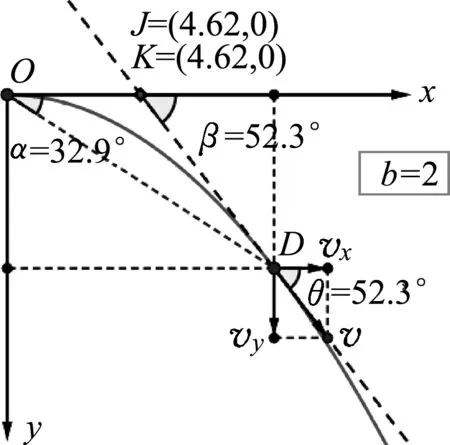
圖2 平拋運動的兩條推論

輸入函數“f(x)=ax2/(x≥0)”，表示平拋運動軌跡.a值與初速度有關，決定拋物線的彎曲程度.構建x、y軸，并在拋物線上描出一點(D點)，作為研究對象.過該點表示速度、位移，并構建速度矢量圖.利用工具欄做出水平位移中點及速度延長線與x軸的交點.通過屬性設置，隱藏一些不必要的點或線，并對顏色、線型、線徑、是否顯示等進行修改，突出主要信息.如圖2所示，移動D點，可發現水平位移的中點J與速度延長線與水平位移的交點K始終重合，位置坐標也保持一致，說明速度延長線確實過水平位移的中點.

在此基礎上，進一步探究速度偏向角與位移偏向角正切值的大小關系.如圖2示，符號b表示速度偏向角與位移偏向角正切值的比值.移動D點，可見b值始終為2，說明速度偏向角正切值始終為位移偏向角正切值的兩倍.

2.3 臨界過程分析的可視化

平拋運動的臨界值問題主要存在于斜面及乒乓球、羽毛球等球類運動過網模型中，分析清楚整個運動情境，找到運動過程的臨界條件，往往就是解題關鍵.下面以2015年理綜全國卷Ⅰ第18題為例，談談如何利用GeoGebra軟件構建物理模型進行可視化分析，更好抓住解題關鍵.

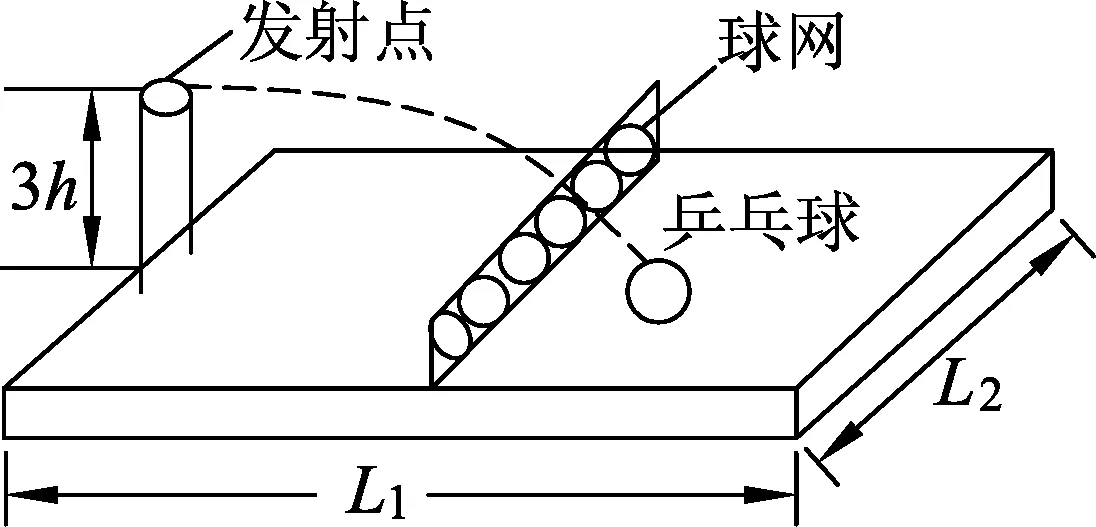
圖3 乒乓球過網模型

一帶有乒乓球發射機的乒乓球臺如圖3所示.水平臺面的長和寬分別為L1和L2，中間球網高度為h，發射機安裝于臺面左側邊緣的中點，能以不同速率向右側不同方向水平發射乒乓球，發射點距臺面高度為3h.不計空氣的作用，重力加速度大小為g，若乒乓球的發射速率v在某范圍內，通過選擇合適的方向，就能使乒乓球落到球網右側臺面上，則v的最大取值范圍是

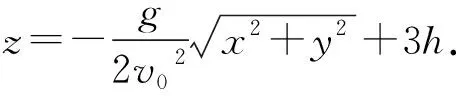
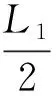
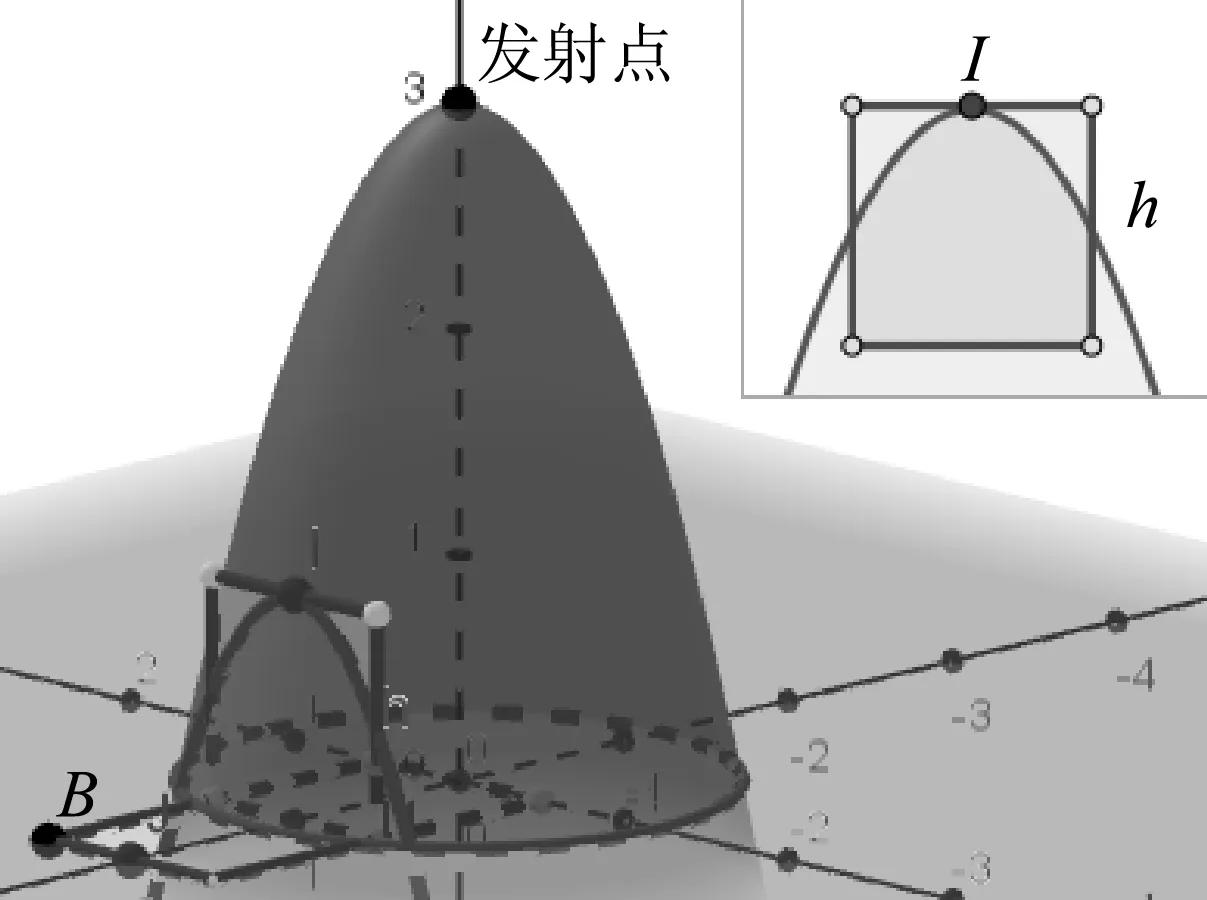
圖4 臨界條件1-不觸網情形

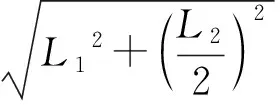
本題容易出錯的地方是對臨界條件2的判斷，學生容易誤認為臨界條件是軌跡過J點.[6]這是因為學生缺乏空間想象力，沒有意識到v0方向的任意性.利用GeoGebra的3D視圖使物理情境立體化、直觀化，能夠幫助學生順利突破這一誤區.在此基礎上，還能改變題給條件，給出L1、L2、h的具體值，要求計算v0的范圍，或是探究L1、L2、h變化對v0和軌跡的影響.GeoGebra軟件能對學生的計算結果進行檢驗，并直觀呈現某條件改變后的影響，強化學生對這一類問題的理解.

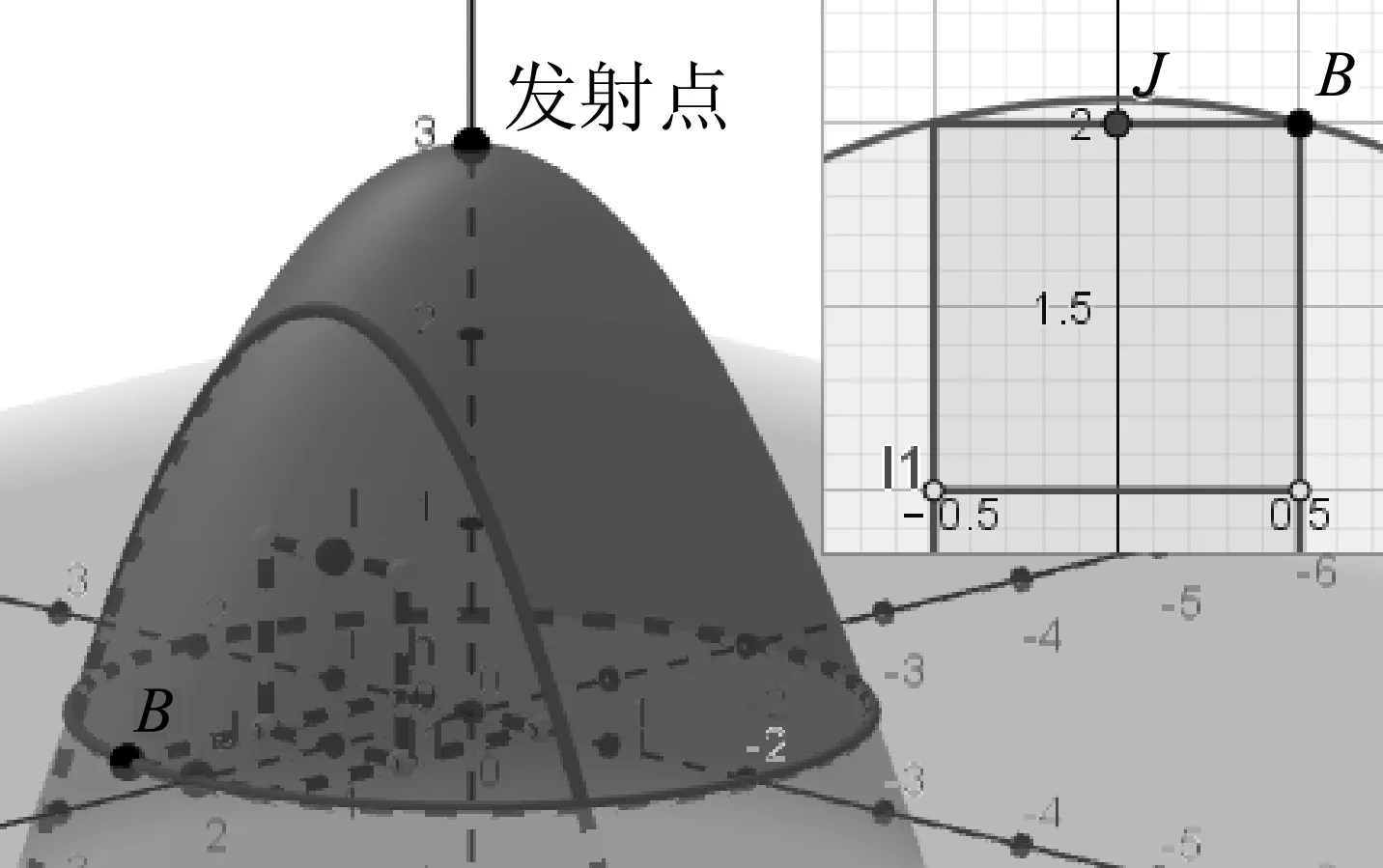
圖5 臨界條件2-不出界情形

3 在其他教學中的應用

3.1 用于抽象概念的形象化

相對于初中階段，高中階段的物理更加抽象，學生在學習過程中存在很多的認知困難.如果不能及時解決這些問題，就會導致學生越學越不懂，漸漸喪失學習興趣.利用GeoGebra軟件能將抽象概念的推導或者理解過程用圖像、動畫等方式呈現，增強學生對抽象概念的形象認知，幫助理解.

例如在電勢的教學中，兩個電荷周圍電勢的疊加是教學的難點，這時可利用GeoGebra軟件的3D繪圖區，通過輸入兩電荷周圍的電勢在空間滿足的方程，呈現電勢的分布情況，使學生獲得感官認識.選擇不同的視圖可觀察不同方向上電勢的分布特征，而對滑動條進行設置還能實現參數的動態調節，顯示如等量同種、異種電荷的三維電勢分布，使電勢具象化.[7]由于z軸代表電勢，則“z=某一具體值”的平面與電勢分布面的交線即為等勢面，還能強化學生對于等勢面的理解.

3.2 用于復雜規律的直觀化

物理規律的教學應著重體現規律背后的思維方法，而這往往較為抽象，且當中可能包含復雜的數學推導，加大了規律教學的難度.這時可以考慮利用GeoGebra軟件將思維方法具體化、數學推導簡單化，使物理規律變得更加直觀.如在勻變速直線運動位移與時間關系的推導中，微元法和極限思想是教學的重點，可以利用GeoGebra軟件展示科學推理的過程，增強思維的可視化.

做出勻變速直線運動的v-t圖像，選定研究區間并劃分為n段.已知勻速直線運動中矩形面積可以表示位移.將每小段視為以該段初速度運動的勻速直線運動，利用“lowersum”指令計算下和值，可粗略表示研究區間的位移.由于每段的實際速度大于或等于該段的初速度，下和值相對于實際位移值應偏小.將每一小段視為以該段末速度運動的勻速直線運動，利用“uppersum”指令計算上和值，同理該值相對實際值應偏大.實際位移總介于上和值與下和值之間，采取二者逼近的方法計算實際位移.[8]

增大n值，下和值增大，上和值減小，均更接近實際位移.當設置的n值較大，兩種矩形構成的圖形幾乎就是梯形，則梯形面積可代表矩形面積，進而代表位移.利用“integral”指令計算圖像面積進行驗證，可見圖像面積始終介于上、下和值之間，且n值較大時三者幾乎無差別，說明勻變速直線運動的位移確實可以用梯形面積表示.

輸入的初速度、加速度及矩形數量均可通過滑動條進行設置，表明該結論具有普遍性，適用于所有的勻變速直線運動.而通過同樣的方法也能對非勻變速直線運動進行探究，彌補實際教學中不規則圖形面積暫時無法計算的遺憾，加深學生對v-t圖像面積含義的理解.

除此之外，像力的合成與分解，重力與萬有引力的關系，兩電荷周圍場強的疊加等復雜規律，也都能利用GeoGebra軟件輔助講解，簡化、直觀.

3.3 用于物理過程的動態化

物理過程往往具有動態性，這時僅通過文字、語言，亦或是圖片難以準確描述其特征，而學生也需要一定的想象力才能理解并還原整個過程，具有一定難度.利用GeoGebra軟件的動態交互功能能對物理過程進行動態模擬，增強情境的真實性.

例如雙星系統的運行.雙星系統是指兩個相距較近，只在彼此引力作用下做圓周運動的恒星組成的系統.前面學生接觸到的都是圍繞中心天體的星體轉動，無法理解像雙星系統這樣圍繞連線上某一點的轉動.利用GeoGebra制作動畫直觀呈現雙星系統的運行機制，便于學生突破這一難點.

除此之外，像追及相遇問題、帶電粒子在電磁場中的運動，甚至是復雜的交流電的產生，也都能利用GeoGebra軟件制作動態變化的效果，幫助理解.

3.4 用于實驗探究的可視化

物理是一門以實驗為基礎的學科，物理中概念規律的建立或多或少都有一定的實驗基礎.利用GeoGebra軟件增強實驗探究的可視化，主要可以表現在以下2個方面.

一是上述提到的數據處理的可視化.除了探究平拋運動的軌跡特點外，利用GeoGebra的多項式擬合功能也能直觀探究兩個不同物理量間的定量關系，如小車速度隨時間變化的規律、自由落體運動的規律、彈簧彈力與形變量的關系等等.后續從擬合函數、圖像斜率等進行分析，能深入理解物理規律，還能得到如加速度、勁度系數等物理量的值，讓學生體驗完整的探究過程，并體會到信息技術的便利及高效.

二是進行模擬仿真實驗，主要針對實際教學不好開展或者是實驗現象不明顯、不直觀的實驗.例如波的疊加，利用GeoGebra軟件的繪圖功能動態呈現兩列波疊加之后的波形圖，甚至探究相關物理量的變化對疊加結果的影響；[9]又如光的干涉，利用GeoGebra軟件以波動的形式動態、立體地展示光的傳播及干涉過程，使整個場景更加鮮活,加深學生對于光的波動性的理解.[10]