非參數Bayesian字典學習的遙感影像融合方法

李 麗

(成都大學 建筑與土木工程學院，四川 成都 610106)

0 引 言

近年來，高光譜(hyperspectral，HS)影像因其所具有的豐富光譜信息，而被廣泛應用于目標的追蹤、識別與分類，以及災害的監測與管理等領域[1-3].依據HS的遙感成像技術，其HS影像雖具有高光譜分辨率與圖譜合一的特點，但由于成像光譜儀設計和制造方面的技術瓶頸，HS影像數據在信噪比、空間分辨率及掃描幅寬等性能方面受到了一定程度的制約[4].相關研究發現，若能獲取同一場景的高空間分辨率影像，則通過影像融合方法便可獲得具有高空間分辨率的HS影像[5-6].對此，科研人員對HS影像和多光譜(multispectral，MS)影像或全色(panchromatic,PAN)影像融合做了大量研究.例如，Aiazzi等[7]利用廣義拉普拉斯金字塔(generalized laplacian pyramid，GLP)的全色銳化方法對HS-MS影像進行了融合；Berné等[8]提出了一種適用于中紅外波段的非負矩陣分解(nonnegative matrix factorization，NMF)的HS-MS影像融合方法；Yokoya等[9]提出了一種利用耦合非負矩陣分解(coupled nonnegative matrix factorization，CNMF)進行光譜解混的HS-MS影像融合方法；Akhtar等[10]利用Bayesian稀疏表示的方法對端元和豐度進行學習來實現HS-MS影像的融合.Wei等[11]利用在線字典學習(online dictionary learning，ODL)進行字典學習，提出一種基于稀疏表示的HS-MS影像融合算法.雖然上述研究成果取得了很好的HS-MS融合效果，但其融合結果對模型的參數設置存在較強敏感性，且無法通過引入更多先驗知識來進一步減少空間信息融入不足和光譜畸變等問題.基于此，考慮到非參數Bayesian方法能夠充分利用圖像的先驗信息，以及對未知參數利用概率估計代替點估計，且在估計過程中引入了不確定性，進而避免了不同參數間估計誤差的擴大等特點[12-13]，本研究提出一種非參數Bayesian字典學習的HS-MS影像融合方法，其特點是可充分利用先驗信息，更好地融入空間信息和保持光譜信息，且具有更小的空間結構誤差及光譜畸變程度.

1 方 法

本研究的目的在于通過對高光譜分辨率的HS影像YH與高空間分辨率的MS影像YM進行融合，以此來恢復具有高空間分辨率的HS影像X.由此，基于HS-MS融合方法的融合過程定義為算法1，具體為：

算法1:非參數Bayesian字典學習的高光譜與多光譜影像融合輸入:YH,YM,NH,NM,B,S,R, mλ,K;%利用高光譜影像YH確定子空間轉換矩陣H^1 H^←PCAYH, mλ();%計算U的粗略估計值 U2 利用文獻[16]中所述方法計算U的粗略估計值 U?μ^U|YM;3 fori=1 to mλdo%利用算法2學習字典元素4 Di←Beta-Bernoulli( Ui);%利用文獻[11]的OMP算法學習稀疏系數5 Ai←OMP( Di, Ui,K);6 end%交替優化7 fort=1,2,...to stopping rule 1 do%利用SALSA[15]及LS[11]對U、A進行交替優化更新8 U^(t)∈U|LU,A^(t-1)()≤LU^(t-1),A^(t-1)(){};9 A^(t)∈A|LU^(t),A()≤LU^(t),A^(t-1)(){};10 end%重建出高空間分辨率的高光譜影像11 Recover X^=H^U^;輸出:X^

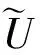
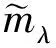
1.1 非參數Bayesian字典及稀疏系數學習

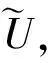
算法2:基于非參數Bayesian的字典學習輸入: Ui,K,τ0,η0,c0,d0,e0,f0;1 從粗略估計值 Ui中選取N個觀測值;2 利用Gibbs抽樣對dk、sik、zik、πk、γ、γs等隱變量進行初始化;3 fori=1,2,...to stopping rule 2 do 4 分別利用公式(6-8)對隱變量dk、sik、zik進行優化更新;5 利用公式(9)對πk進行優化更新;6 利用公式(10)對γ進行優化更新;7 利用公式(11)對γs進行優化更新;8 end9 計算dk的平均值;輸出: Di

算法2中，各隱變量對應的抽樣公式分別為,

p(dk|-)∝

(6)

p(sik|-)∝

p(zik=1|-)∝

(8)

p(πk|-)∝

Beta(c0η0,c0(1-η0))

(9)

p(γ|-)∝

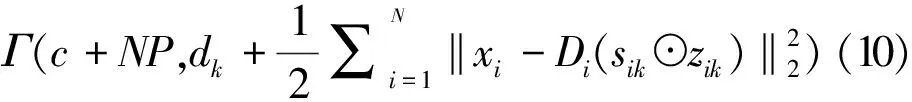
p(γS|-)∝

(11)

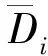
1.2 交替優化的模型求解

在交替優化過程中，算法1融合框架中的該優化問題為一個標準的關于U和A的二次約束優化問題.

由于矩陣間運算維數較高，且相關算子難以對角化，因此，該類約束優化問題通常很難進行求解.為解決此問題，本研究選擇先固定稀疏系數A更新矩陣U，然后固定U更新A的交替優化算法對U和A進行聯合優化更新.在該步驟中，本研究采用SALS算法和LS算法來分別解決目標影像U及對應稀疏系數A的約束優化問題(見算法1中第9步).

2 結果與分析

為驗證所提方法的有效性，本研究選取HS-MS融合方法中較為流行的GLP[7]、CNMF[9]和SRFM[11]3種算法與本文方法進行仿真實驗比較，并采用重構信噪比(restored signal noise ratio，RSNR)、均方根誤差(root mean square error，RMSE)、光譜角填圖(spectral angle mapper，SAM)、通用圖像質量評價指標(universal imagequality index，UIQI)、相對全局融合誤差(erreur relative globale adimensionnelle de，ERGAS)和畸變程度(degree of distortion，DD)6個評價指標[18]對融合結果進行定量評價.其中，RSNR、UIQI值越大，融合質量越好；RMSE、SAM、DD及ERGAS值越小，融合質量越高.

2.1 實驗數據

在實驗中，參考影像采用由ROSIS(reflective optics system imaging spectrometer)傳感器于2013年獲取的位于意大利帕維亞地區的空間分辨率為1.3 m，像素大小為610×340的高空間分辨率高光譜影像.該原始影像共包含115個光譜波段,波長覆蓋范圍為0.430～0.838 μm[18].去除12個強噪聲波段及10個水汽吸收波段，本研究分別選取128×128×93(圖1中場景1)及256×256×93(圖1中場景2)大小的ROSIS影像數據進行兩組仿真實驗.分別取紅、綠、藍3個波段，場景1及場景2所合成的假彩色影像如圖1所示(為便于顯示，以下場景1、場景2的相關影像均分別以原始像素的90%及50%比例顯示).

(a)場景1

在ROSIS影像數據的場景1及場景2的融合實驗中，分別對ROSIS參考影像X的每個波段進行5×5高斯空間濾波，然后在水平和垂直方向進行4倍下采樣后得到HS影像YH.同時，使用IKONOS-like波譜響應[18]對參考影像X進行光譜降質，得到含有4個光譜波段的MS影像YM.然后對YH和YM均添加加性零均值高斯噪聲，假定YH的前43個波段信噪比為35 dB，剩余50個波段信噪比為30dB，YM各波段影像信噪比均為30 dB.

2.2 參數設置

2.2.1 低維子空間學習

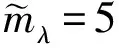
2.2.2 字典學習

2.3 結果分析

ROSIS數據的場景1與場景2在GLP[7]、CNMF[9]和SRFM[11]及本文方法下的融合結果如圖2、圖3所示.其中，3種對比算法的實驗參數均參考原文獻取值.

(a)參考影像

由圖2、圖3可看出，本文方法的融合效果明顯優于GLP[7]、CNMF[9]算法，略優于SRFM[11]算法，尤其表現在圖2中白色地物區域處，以及圖3中建筑物邊緣紋理處，本文方法的細節恢復能力更強.其主要原因在于利用非參數Bayesian方法進行字典學習，能夠通過引入更多的先驗信息來提高字典元素對目標影像結構和紋理信息的表達能力，從而進一步提升融合結果的質量.

(a)參考影像

為更加直觀地觀察不同融合算法下的融合結果在細節處的差異，本研究引入差值圖[10]，即參考影像與融合影像之間的絕對誤差圖來進行主觀評價，點越亮代表差值越大，暗點則表示差異性小.場景1與場景2在不同算法下融合結果的絕對誤差如圖4、圖5所示.

(a)參考影像

由圖4、圖5可看出，本文方法的融合結果的絕對誤差均遠小于GLP、CNMF算法，而略小于SRFM算法，且誤差分布的趨勢符合圖2、圖3的目視對比結果.此也進一步證明了本文方法的有效性.

(a)參考影像

此外，除了上述主觀評價，表1、表2分別給出場景1與場景2在各算法下融合結果的客觀評價指標數據.

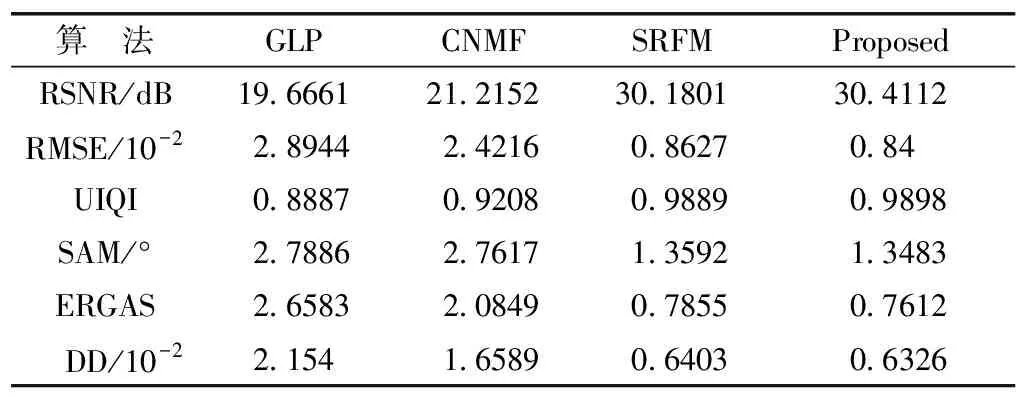
表1 ROSIS場景1不同算法下的定量評價指標數據

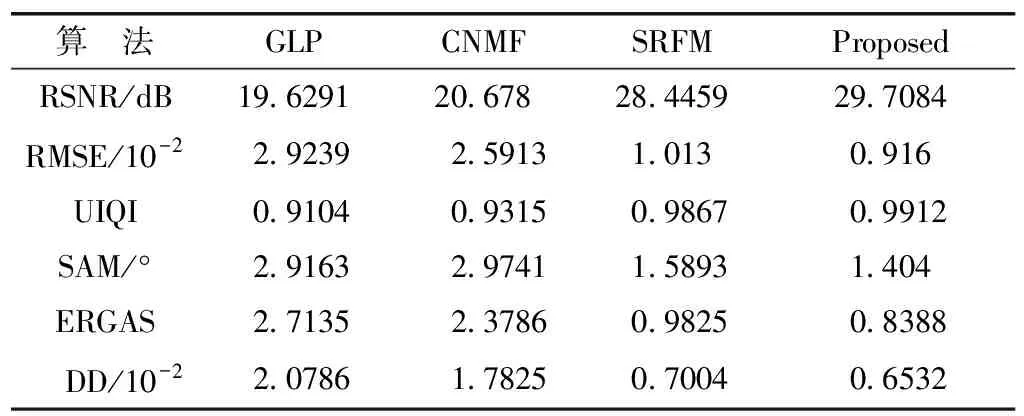
表2 ROSIS場景2不同算法下的定量評價指標數據

由表1、表2中PSNR、RMSE、SAM、UIQI、ERGAS和DD值可看出，本方法的融合效果仍為最優.此也進一步證明了客觀評價結果與上述主觀評價結果的一致性.

3 結 論

針對高光譜影像難以兼具高空間分辨率及高光譜分辨率進而在一定程度上限制了其應用領域的問題，本研究在文獻[11]所提融合算法的基礎上提出一種基于非參數Bayesian字典學習的高光譜與多光譜影像融合方法.該方法在子空間內進行影像融合：首先，利用Beta Bernoulli過程對投影至低維子空間的高光譜與多光譜影像進行字典學習，獲得字典元素的后驗分布；然后，利用OMP算法進行稀疏系數學習；最后，利用ADMM算法結合SALS算法與LS算法對目標影像和對應的稀疏系數進行交替優化更新，從而獲得具有更高空間分辨率的高光譜影像.與當前流行的幾種HS-MS算法相比，本研究方法融合結果的空間結構誤差和光譜畸變程度相對較小，兩組仿真實驗中其融合結果均具有最優的目視效果及定量評價指標結果.其主要原因在于本研究所采用的非參數Bayesian方法能夠在字典學習的過程中引入更多先驗信息，從而提高字典元素的表達精度以及目標影像的估計精度.值得注意的是，本研究方法采用Gibbs進行迭代抽樣，字典元素的后驗分布依賴于大量的迭代抽樣，因此其計算效率相對較低，下一步的工作將探討引入變分貝葉斯等快速近似解求解方法以提高算法的計算效率.