基于改進貝葉斯網絡和Hausdorff距離的電網故障診斷

劉道兵 余夢奇 李世春 代 祥

(1.三峽大學 電氣與新能源學院，湖北 宜昌 443002；2.梯級水電站運行與控制湖北省重點實驗室(三峽大學)，湖北 宜昌 443002；3.國家電網湖北省電力有限公司 應城供電公司，湖北 應城 432400)

近年來，我國電網規模不斷擴大，電網結構也日益復雜，電網自身面臨的內部及外部環境影響的風險也在不斷增大；當電力系統出現故障后，為了盡可能減小電網故障對人們生產生活的影響，需要及時快速地鎖定故障元件，而安裝在系統中的各種監測裝置能夠實時監控電網的運行狀態并儲存下來，這些信息可作為整個系統事故后的診斷和評價依據.

現有的電網故障診斷方法主要有專家系統[1]、模糊Petri網[2]、貝葉斯網絡[3]、人工神經網絡[4]、解析模型[5]等，這些方法主要利用開關量信息進行診斷分析，對于告警信息中的時序信息以及暫態電氣量信息并沒有充分利用.文獻[6]在解析模型的基礎上，考慮到保護裝置在動作過程中存在不確定性，提出了計及保護拒動和誤動的解析模型，但是直接用告警信息代替實際狀態，沒有考慮保護裝置在不同狀態下的動作可信度，在開關量信息丟失或者告警信息發生畸變的情況下，容易產生多解，甚至是誤解.文獻[7]在其基礎上引入電氣量信息，建立電氣量判據并加入到模型中，雖然一定程度上提高了診斷準確性，但是增加了模型的維度，不利于模型的快速求解.文獻[8]通過對數據源進行分類，提取對應的故障特征量，采用D-S數據融合的方法得出最終的元件故障概率，該方法直接將剩余信度賦值給框架本身，在信息融合的過程中證據體之間存在沖突較大的情況下會得出與實際情況不相符的結果.針對上述文獻所提及方法存在的不足，本文在已有的貝葉斯模型上對網絡中事件節點動作的時間和狀態分別利用模型和關聯規則進行可信度評估，實現從開關量到故障度的轉化.將暫態電氣量信息加入到診斷證據源中，利用小波分解重構提取暫態電氣量中的故障幅值特征，采用Hausdorff距離算法轉化成對應的暫態故障度，兩種證據源采用證據推理(evidence reasoning，ER)規則進行信息融合決策，得到最終的診斷結果.

1 基本理論

1.1 因果關聯規則

因果網絡(cause-effect net，CEN)規則是對事件發生的起因和結果進行圖形化建模的工具，利用該規則建立電網中的元件和保護裝置之間存在的邏輯關聯關系.

1)元件故障導致與其關聯的保護動作；

s=1?r?=1|?r∈R，s∈S

2)保護動作導致與其關聯的所有斷路器動作；

r=1?c?=1|?r∈R，c∈C

3)若某一斷路器動作，則與其有關聯關系的任一保護也應正確動作：

c=1?r⊕=1|?r∈R，c∈C

對于由元件故障最終導致斷路器跳閘的這一系列事件可以由關聯路徑P(vi，vj)描述.定義For(vi)表示節點vi發生導致所有相繼發生的節點事件集合，Back(vj)為可能導致vj發生的節點事件集合，則：P(vi，vj)={vk|vk∈For(ri)∧vk∈Back(vj)}.

1.2 改進貝葉斯網絡

假設集合變量X={x1，x2，…，xn}，xn表示網絡中有n個節點，當出現多個節點同時發生的概率為

p(x1，…，xn)=p(x1)p(x2|x1)…

(1)

式中：π(xi)為xi的父節點集合，針對每一個xi，其對應的有m個關聯基本事件{e1，…，em}.假設除了xi之外，網絡中的其他節點的狀態通過先驗概率已經獲得E={x1，…，xi-1，xi+1，…，xn}，則事件節點xi對應的第s個事件es發生的條件概率[9]：

(2)

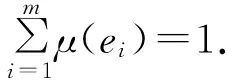
2 多源信息處理

2.1 靜態開關量信息的獲取和處理

故障發生后，依據電網拓撲結構和邊界斷路器跳閘狀態確定故障發生的區域以及待診斷元件，利用關聯關系建立待診斷元件的貝葉斯網絡模型，針對每一個事件節點中包含的時序信息和動作狀態按照以下方法進行可信度評估.

2.1.1 時序可信度

由于在實際電力系統中，存在信息上傳不及時以及傳輸效率的影響，其節點動作時間在一定范圍內波動則認為其時序是可信的.

保護動作的時間點約束：

T(p)=[t0+tp-τp，t0+tp+τp]

(3)

式中：t0為故障發生時刻；tp為各個保護的整定值；τp為保護最終動作所允許的誤差范圍.

斷路器動作的時間點約束：

T(c)=[t1+tc-τc，t1+tc+τc]

(4)

式中：t1為關聯保護發出跳閘信號的時間；tc為斷路器的分閘時間；τc為斷路器最終動作所允許的誤差范圍.

對各個節點的時序信息進行約束定義后，可得：

T(s→p)=[tp-τp，tp+τp]

(5)

T(p→c)=[tc-τc，tc+τc]

(6)

時序一致性約束：

(7)

對于滿足時序約束范圍內的不同區段的事件賦予不同的可信度.

(8)

式中：T、τ的實際值根據保護或斷路器動作來取對應的值.

本文設置的保護裝置動作的延時數據見表1，所有數據值均基于元件所發出的信號.

表1 保護裝置延時數據的設定

2.1.2 狀態可信度

定義：fr表示保護的期望狀態，lr、mr為保護告警信息的漏報、誤報，dr、wr為保護的拒動、誤動.并將其描述成fr，r′；(r，mr，lr，wr，dr).

規則1：當s=1時，存在以下幾種發展情況：

當相應主保護拒動時，

當近后備保護因為拒動或者在其保護范圍內的關聯線路上還有其他故障沒有被完全隔離時，

規則2：當s=0時，保護動作狀態：

規則3：當任一保護動作時，則斷路器的狀態：

規則4：當保護沒有動作時，斷路器的狀態：

結合告警信息，按照以上規則推導可以得到所有待診斷元件所關聯的保護裝置的狀態組合.對于不同組合里的保護裝置其動作可信度存在一定差異，結合推導的實際狀態與期望狀態值，需要對其動作狀態進行可信度評估得到βstate，本文參考文獻[10]中所述方法，對獲得的保護裝置的動作狀態和期望狀態進行對比賦值見表2.

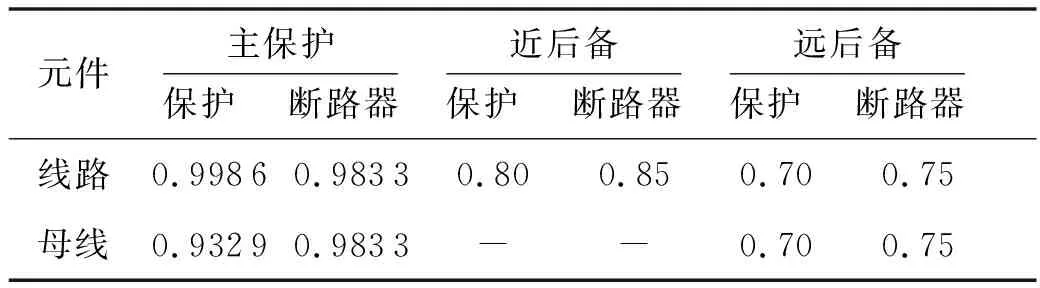
表2 保護裝置可信度設定

結合以上對開關量信息中包含的時序信息和狀態信息的可信度評估，對于動作事件，其節點動作的可信度為：

μ(e=1)=ω1βstate(e=1)+ω2βtime(e=1)

(9)

其節點動作的不可信度為：

μ(e=0)=1-μ(e=1)

(10)

式中：w1，w2分別為時序可信度和動作狀態可信度相對權值，其值取0.55、0.45時有較好的診斷效果，得到每個節點事件綜合可信度后，結合式(2)，可以計算得到待求元件的靜態故障率.

2.2 暫態電氣量信息的獲取和處理

將 Hausdorff距離算法[11]引入到暫態電氣量信息的處理過程中，利用Hausdorff距離算法識別暫態電流的幅值差異，并以此作為元件是否故障的獨立證據源.Hausdorff 距離算法為

H(A，B)=max(h(A，B)，h(B，A))

(11)

(12)

(13)

式中：A、B為電氣量信息的采樣點集合，A={a1，…，an}，B={b1，…，bn}，|ai-bj|表示集合A中點ai到集合B中點bj的距離，通過式(12)、(13)計算可以得到n個距離，再通過式(11)得到Hausdorff距離H(A，B).

基于以上計算原理，Hausdorff算法不受微弱信號的干擾，而且能夠計算出信號間的幅值差異程度，定義在t時刻H距離的變化率為at，則變化率的計算公式：

(14)

提取故障發生時刻前后各n個周期的電流信號，得到的變化率發生突變的概率：

(15)

在該時間段內，對H距離發生突變的概率進行積分，可以得到基于暫態電氣量的故障度：

(16)

3 ER規則的信息融合診斷模型

為了使故障特征更好地表現出來，對所有可能表現出沖突的結論進行綜合分析，建立ER規則的信息融合診斷模型.本文將開關量故障度和電氣量故障度作為獨立證據體，將待診斷故障元件集用Θ作為識別框體，Θ={m1，m2，…，mp}，集合Θ的冪集記為P(Θ)或2Θ，對兩種不同的證據體構建可信度分配函數，從不同的信息源中得到的證據被定義為：

(17)

式中：(θ，pθ，j)表示ej支持θ的信度為pθ，j，θ為P(Θ)中的任意元素.

ER規則中，加入可靠因子rj表示證據ej對應的信息源能夠對給定元素的可信度評估，wj定義了ej對于其他證據的重要性權重，其定義如下[12，13]：

(18)

(19)

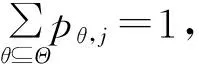
(20)

(21)

(22)

式中：r1=0.8，r2=0.6，w1=0.9，w2=0.6，利用ER 規則進行融合，從而可以得到兩個獨立證據源對可疑故障元件集中一個或者多個故障元件的決策程度.

為了使融合結果更加準確，經過實際數據進行反復融合，設置0.83作為元件是否發生故障的臨界值.若融合結果大于0.83，則認定該元件為故障元件.

4 診斷流程

診斷流程圖如圖1所示.

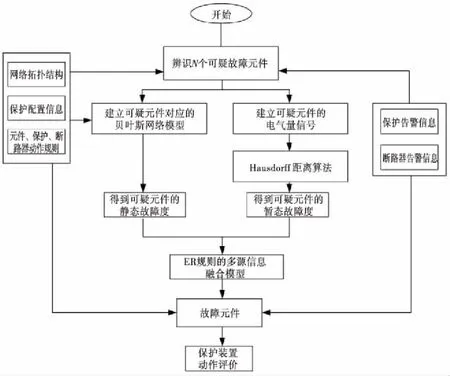
圖1 診斷流程圖

步驟如下：

1)根據系統拓撲圖和斷路器開合狀態確定故障區域和可疑故障元件；

2)利用因果關系推理關聯路徑，建立待診斷元件的貝葉斯網絡，對每個節點進行時序和狀態評估，推理出元件的靜態故障概率；

3)利用小波分解重構得出元件暫態特征量，結合Hausdorff距離算法得到元件的暫態故障概率；

4)ER推理規則對靜態開關量故障概率和暫態電氣量故障概率進行融合決策，得出診斷結果；

5)將最終的診斷結果結合對應元件的貝葉斯網絡模型，得到故障發生的推演結果和保護裝置動作評價.

5 算例分析

本文以IEEE14節點系統為例驗證所提方法的可行性，如圖2所示.

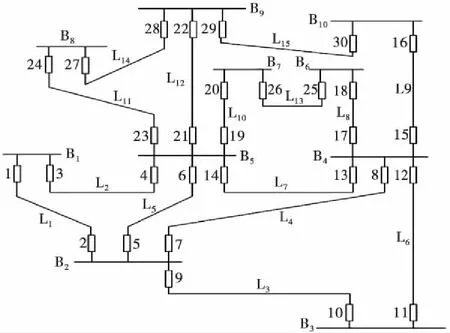
圖2 IEEE14節點系統圖

1)算例1：復雜故障下存在保護裝置拒動情況

以圖2為例，故障設置情況：母線B5和線路L15分別發生故障，斷路器CB23發生拒動，線路L11靠近母線B8一側遠后備保護動作導致斷路器CB24發生跳閘，線路L15靠近母線B10一側主保護發生拒動，由同一側的近后備保護動作，斷路器CB30跳閘.其動作情況見表3.

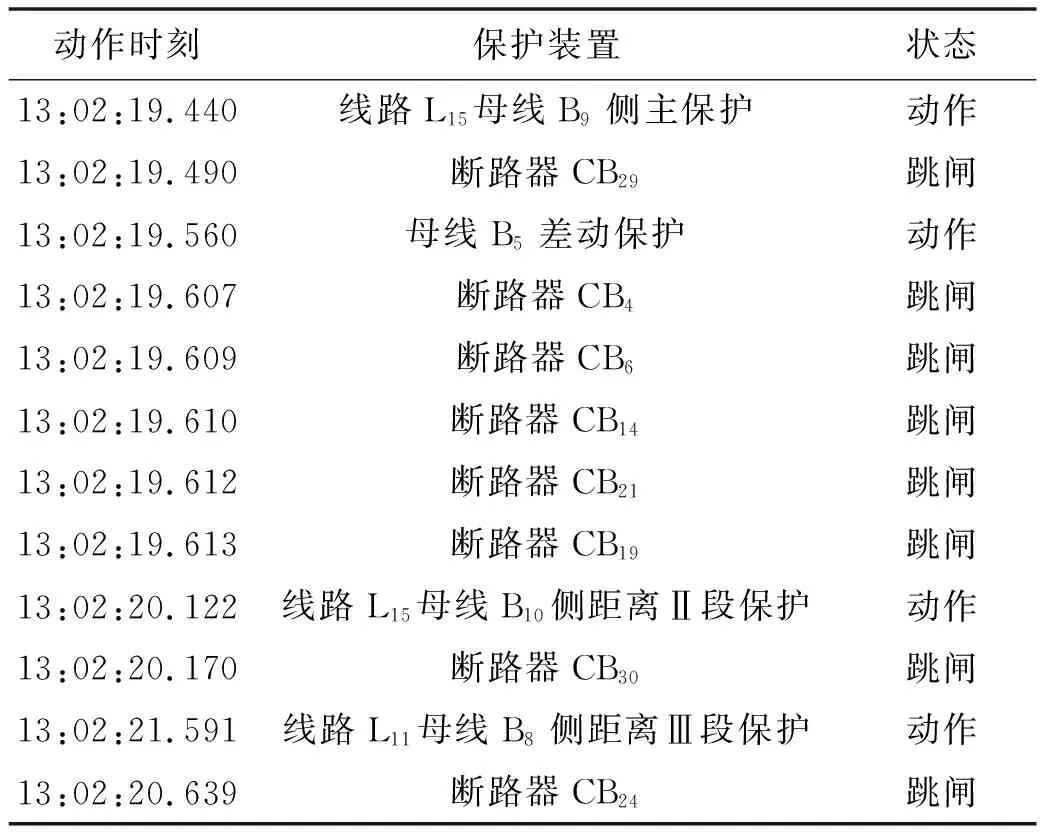
表3 保護裝置動作情況

根據拓撲圖和斷路器確定故障區域和可疑元件集S={B5，L15，L11}，利用因果關聯規則建立每一待求元件的貝葉斯診斷模型.

以線路L15發生故障為例，依據關聯規則建立線路L15對應的貝葉斯網絡模型如圖3所示.其中，f為斷路器失靈保護.

圖3 線路L15貝葉斯網絡模型

對路徑上節點事件的時序和動作狀態按照2.1節所述方法進行可信度評估和靜態故障度求取，得到結果分別見表4、表5.

表4 線路L15上動作節點可信度結果

表5 元件L15靜態故障度

同理，構建元件B5和L11的貝葉斯網絡模型，求出其節點可信度，將其轉化為對應的故障度見表6.

表6 元件、靜態故障度

提取元件兩端的暫態電流信號，進行分解重構后利用2.2節中Hausdorff距離算法求出其暫態故障度.結合獲取的靜態和暫態故障測度，利用ER規則進行證據融合，得到證據融合結果見表7.

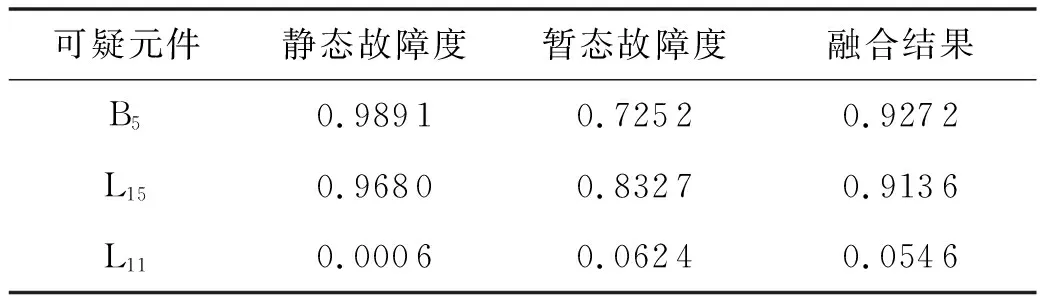
表7 融合結果

從表7融合結果來看，其融合結果值大于0.83，可以判定元件L15、B5為故障元件.結合元件貝葉斯網絡模型作正向推理，得到斷路器CB12、L11-(8)m發生拒動，這與實際情況相符，綜合以上情況得到完整故障推演結果：

B5推演結果：B5→CB4→CB6→CB14→CB21→CB19→L11-(8)s(CB23拒動)→CB24；

L15推演結果：L15→L15-(9)m→CB29→ L15-(10)p(L11-(8)m拒動)→CB30.

2)算例2：復雜故障下存在保護裝置拒動和誤動

故障設置情況：以圖2為例，線路L2和線路B4同時發生故障，線路L2靠近母線B5側斷路器CB4跳閘，母線B1側斷路器CB3拒動，線路L1靠近母線B2側斷路器CB2跳閘，線路L7上斷路器CB14發生誤動，斷路器CB17發生拒動.L9-(4)m未動，導致L9-(4)p動作.

按照2.1和2.2所述方法進行診斷，其診斷結果見表8.

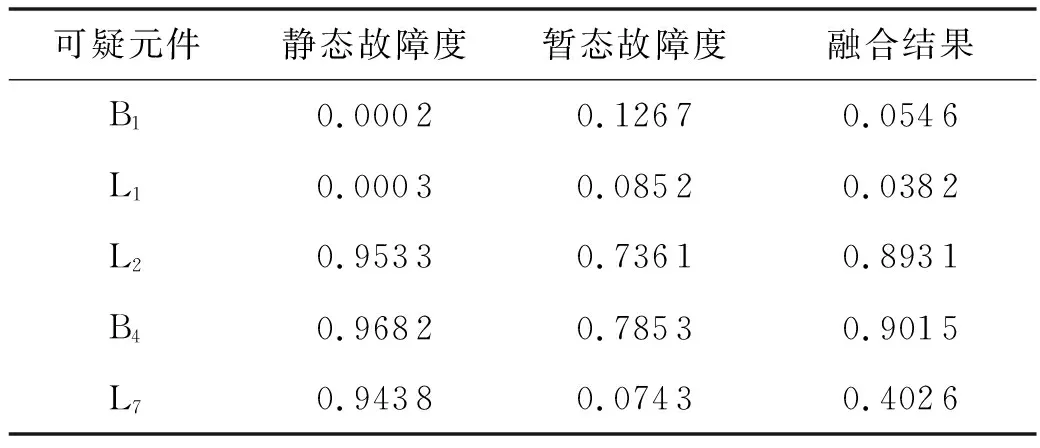
表8 融合結果

根據融合結果，元件B4、L2的融合值大于0.83，判定故障元件為B4、L2，結合故障元件貝葉斯網絡得到斷路器CB17、L9-(4)m發生拒動，CB14誤動，如果按照文獻[5]中所提方法，只考慮開關量信息為診斷依據，容易造成線路L7被診斷成故障元件，加入暫態信息量后，可以排除這個誤診元件.同理可以得到推演過程：

B4推演結果：B4→CB12→CB8→CB13(CB14誤動)→CB17→L9-(4)p(L9-(4)m拒動)→ CB15；

L2推演結果：L2→CB4→CB3拒動→L1-(2)s→CB2.

6 結 語

提出了一種基于改進貝葉斯網絡和Hausdorff距離的多源信息融合電網故障診斷方法.通過對開關量和電氣量信息的提取和處理，轉化成對應的元件故障度，完整地保留了故障信息的冗余性，有效避免了信息不完備、保護裝置動作不可靠對診斷結果的影響.采用ER規則進行融合，可以解決證據沖突時造成的診斷結果誤差.仿真結果表明該方法在保護裝置發生拒動和誤動的情況下依舊能夠準確判定出故障元件，提升了診斷的可靠性，并能對故障演變進程進行解釋，能很好地適應復雜故障下的診斷.