基于改進卡爾曼濾波的大規模MIMO信道預測方法

鄭添月，凌泰煬，姚志偉，王聞今，李 瀟，金 石

(東南大學 信息科學與工程學院，江蘇 南京 211100)

0 引言

大規模多輸入多輸出(Multiple-input Multiple-output,MIMO)技術與正交頻分復用(Orthogonal Frequency Division Multiplexing,OFDM)技術的結合被認為是B5G和6G的關鍵技術之一[1]。OFDM技術由于能夠在頻率選擇性衰落信道中減輕時延擴展的影響而得到廣泛應用[2]。而大規模MIMO技術，通過使用多個發射和多個接收天線，使得系統能夠在不擴展額外帶寬的情況下顯著增加信道容量[3]。在大規模MIMO-OFDM系統中，獲得可靠的信道狀態信息(Channel State Information，CSI)尤為重要。例如，大規模MIMO多用戶下行鏈路傳輸需要在基站(Base Station,BS)端基于CSI進行預編碼以消除用戶側的同信道干擾[4]；大規模MIMO系統通常基于CSI的自適應傳輸在時變信道中選擇最佳的調制與編碼方式以提高吞吐量[5]。然而，在移動環境下，由于基站和用戶的相對移動以及信道時變特性，通過信道估計獲得CSI往往會過時，嚴重影響大規模MIMO系統的性能[6]。

信道預測是一種有效解決移動環境下CSI過時問題的技術。通過利用CSI的時間相關性，信道預測能夠利用過去時刻的信道信息預測當前時刻的信道信息，從而有效解決CSI過時的問題。在時分雙工(Time Division Duplex,TDD)系統中，上行鏈路CSI是通過上行探測導頻獲得的。例如，在5G標準中，上行探測導頻是在TDD系統中承載大量MIMO導頻的主要候選信號[7]。在TDD系統中，利用上行鏈路和下行鏈路的信道互易性[8]，發射機能夠將估計的上行鏈路CSI作為時不變信道中所需的下行鏈路的CSI進行信道預測，而無需通過用戶端反饋獲得下行鏈路的CSI。TDD模式是當前大量部署的移動通信系統的主要雙工模式。在這種背景下，本文針對廣泛使用的TDD進行信道預測研究。

信道預測問題一直以來在學術界受到廣泛關注。文獻[9]提出了在大規模MIMO-OFDM不同信道域，即天線頻率域、天線時延域、角度頻率域和角度延時域下的自回歸(Autoregressive,AR)的信道預測方法，并驗證了角度時延域的預測性能比其他3個預測域具有更高的精度。然而，文獻[9]所提出的AR模型無法在有噪聲的環境下充分利用CSI的時間相關性。除此之外，文獻[10]提出基于CSI時間相關性的卡爾曼濾波器預測模型，然而基于卡爾曼濾波器的模型包含AR參數計算和基于卡爾曼濾波的信道估計兩部分，計算復雜度較高，限制了它們在實際有噪信道中的應用。雖然目前在文獻[11-12]中已經提出各種改進的卡爾曼估計器來降低計算復雜度，但是它們都沒能充分利用CSI的空間相關性以改善預測性能。

為解決上述現有信道方法存在的問題，本文基于上行探測導頻信道估計，提出一種基于改進卡爾曼濾波的大規模MIMO-OFDM信道預測方法,該方法利用信道信息的空間和時間相關性，在噪聲環境下的無線信道預測中，該模型在不增加太多計算復雜度的情況下，可以獲得比上述文獻更優的預測性能。

1 系統描述及信道模型

1.1 大規模MIMO-OFDM系統概述

根據圖1所示，大規模MIMO-OFDM系統包含Nt根發射天線和Nr根接收天線。因此，大規模MIMO信道由Nt×Nr個傳播子信道組成。在時刻n，輸入數據可表示為:

x[n,k]=[x(1)[n,k]x(2)[n,k]…x(Nt)[n,k]]T,k=1,2…K，

(1)

式中，x(i)[n,k]表示時刻n第i根發射天線、第k個子載波的發射符號，K為子載波的數量，上標 “T” 表示轉置運算符。然后，OFDM使用離散傅里葉逆變換(Inverse Discrete Fourier Transform,IDFT)來調制發射信號，相應地，在接收端使用離散傅里葉變換(Discrete Fourier Transform,DFT)來解調接收信號。插入一個長度為LCP的循環前綴(Cyclic Prefix,CP)，在第u根接收天線處接收到的天線頻率域信號可以表示為:

(2)

式中，H(uv)[n,k]，v(u)[n,k]分別代表第v根發射天線到第u根接收天線在第k個子載波上的頻率響應和加性高斯白噪聲(Additive White Gaussian Noise,AWGN)。

與發射端信號類似，定義在時刻n，第k個子載波的接收信號、信道頻率響應和噪聲分別為：

y[n,k]=[y(1)[n,k]y(2)[n,k]…y(Nr)[n,k]]T，

(3)

(4)

v[n,k]=[v(1)[n,k]v(2)[n,k]…v(Nr)[n,k]]T。

(5)

因此，根據式(2)，接收信號可以寫為：

y[n,k]=H[n,k]x[n,k]+v[n,k]。

(6)

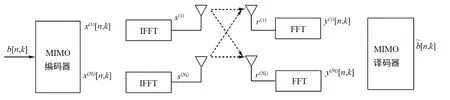
圖1 MIMO-OFDM發射接收原理示意圖Fig.1 MIMO-OFDM schematic diagram of transmitting and receiving

1.2 系統架構及信道模型

本文的目標是利用過去時刻的CSI來對當前或者未來時刻的CSI進行預測，解決CSI過時的問題。本文的關鍵內容及其流程架構總結如圖2所示。如上文討論，為減少獲取CSI的開銷，發射機可以使用估計到的上行鏈路CSI代替下行鏈路CSI來預測所需的下行鏈路CSI。

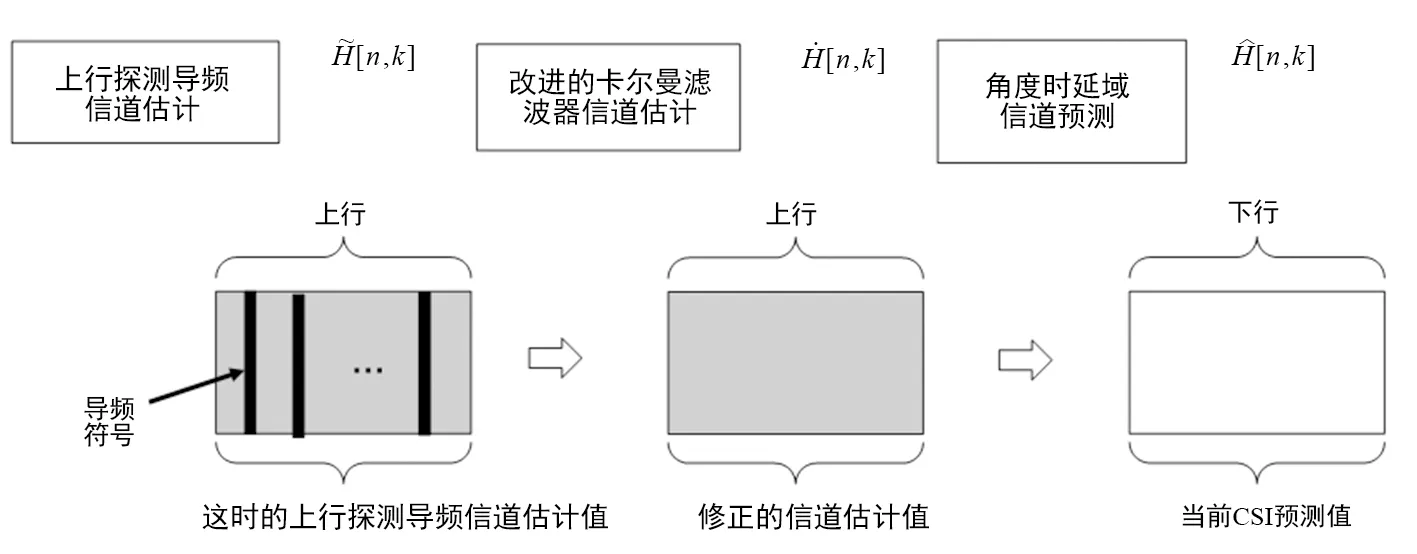
圖2 本文關鍵內容架構Fig.2 Framework of focus of the paper

在實際情況下，上行鏈路CSI估計值與實際值存在誤差。因此，在進行信道預測之前，本文采用一種改進的卡爾曼濾波器信道估計模型來修正上行鏈路CSI估計值，以達到更好的預測精度。下面簡要介紹利用上行探測導頻進行信道估計的過程[7]及信道矩陣測量值的表示，后兩個步驟，作為本文提出模型的核心內容，將在下一部分詳細討論。

假設第m個用戶到第b個基站的導頻序列為NP×1的矩陣φm,b,其中NP表示導頻序列的長度，那么，由基站b調度的M個用戶使用的上行探測導頻序列的復合矩陣可表示為Φb=[φ1,bφ2,b…φM,b]。同一BS小區內，假設不同用戶使用的上行導頻序列都是相互正交的，因此有ΦbΦbT=IM，其中IM為M×M的單位矩陣。因此，在第b個基站處通過天線接收的每個時頻資源的上行探測導頻信號Zb可以表示為：

(7)

式中，ρ表示用戶向其上行探測導頻施加的上行鏈路發射功率，Hb,j為第b個基站與第j個基站調度的用戶之間的上行鏈路信道矩陣，Ub為上行鏈路信道加性高斯白噪聲矩陣。

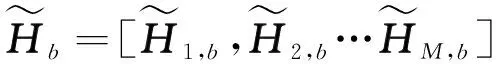
(8)

(9)

式中，N(uv)[n,k]為第v根發射天線到第u根接收天線間的噪聲，服從均值為0、方差為σ2的高斯分布。

1.3 不同域下的信道表征

如文獻[9]中所提出的，大規模MIMO-OFDM信道可以從兩個維度對其進行表示的分類：前者與大規模MIMO技術相關，分別可以在天線域(ARD)與角度域(AGD)中表示；后者與OFDM技術相關，分別可以在頻域(FD)與時域(TD)中表示。因此，MIMO-OFDM信道的表示方法可以分為4個組合域：天線頻率域(AR-FD)、天線時延域(AR-TD)、角度頻率域(AG-FD)和角度時延域(AG-TD)[12]。

在上一節中，AR-FD中的信道可表示為H[n,k]，在本小節將給出其他3個域中的信道表示方法。MIMO-OFDM信道在AR-TD中可表示為G[n,l],l=1,2…Ng，其元素H(uv)[n,l]表示第v根發射天線到第u根接收天線間第n個OFDM符號的第l個抽頭的信道信息，Ng為信道抽頭數。AR-TD中的信道可以由AR-FD中的信道通過IDFT實現，該過程可表示為：

(10)

接著，角度頻率和角度時域的信道表示可以由AR-FD和AR-TD的信道通過變換得到：

(11)

(12)

其中，H′[n,k],G′[n,l]分別為AG-FD和AG-TD中的信道表示。前者的元素為H′(αβ)[n,k]表示在時刻n，子載波k上，第β個發射角度到第α個接收角度的信道增益矩陣；后者的元素為G′(αβ)[n,l]表示在符號時刻n，信道抽頭l上，第β個發射角度到第α個接收角度的信道增益矩陣。Ur,Ut分別為Nr×Nr，Nt×Nt酉矩陣，其第(k,l)個元素分別為:

(13)

(14)

2 基于改進卡爾曼濾波器-AR的信道預測

在此部分中，提出了一種基于上行探測導頻信道估計的信道預測方法，該方法同時利用CSI的空間和時間相關性以提高預測精度。如上所述，所測信道狀態信息矩陣中包含噪聲，因而影響了CSI的時間相關性。在這種情況下，自回歸預測方法不能充分利用實際噪聲環境下CSI的時間相關性，預測性能較差。因此，本文首先利用改進的卡爾曼濾波器，利用過時信道信息對測量數據進行修正，以獲得更好的時間相關性，在此基礎上再采用AR方法進行信道預測。

需要注意的是，在本節只給出了AG-TD中的預測方法，其他3個領域中的方法可以按照類似的方法給出。

2.1 基于改進卡爾曼濾波器的信道估計方法

在第一階段，為了減小噪聲的影響，提高預測性能，利用改進的卡爾曼濾波對信道進行估計，加強信道信息的時間相關性。然而，傳統的卡爾曼濾波主要包括兩個步驟：第一，基于自回歸的參數估計；第二，利用卡爾曼濾波理論估計信道增益。這使得傳統方法計算復雜度較大，因而限制了其在實際無線系統中的應用。本文利用文獻[11]中提出的一種改進的卡爾曼濾波方法，在降低計算復雜度的同時，仍然獲得了CSI時間相關性的提高。

為表達方便，記X(αβ)[n,l]為：

X(αβ)[n,l]=[G′(αβ)[n,l]G′(αβ)[n-1,l]…

G′(αβ)[n-p+1,l]]T,

(15)

式中，p代表模型的階數。因此，狀態方程可表示為：

X(αβ)[n+1,l]=ΦX(αβ)[n,l]+GCw(αβ)[n+1,l],

(16)

其中,轉態轉換矩陣Φ，Gc和w(αβ)[n+1,l]分別可表示為：

(17)

Gc=[1O1,p-1]T，

(18)

w(αβ)[n+1,l]=G′(αβ)[n+1,l]。

(19)

接下來，根據式(2)，觀測方程可以表示為：

y(αβ)[n,l]=MX(αβ)[n,l]+v(αβ)[n,l]，

(20)

其中，M矩陣定義為M=[1O1,p-1]，可以得到以下表達：

(21)

下面，應依據以下方程初始化狀態矩陣和關系矩陣：

(22)

遵循以下方程，可以使用卡爾曼濾波來估計接收信號的信道增益：

(23)

P(αβ)[n|n-1,l]=ΦP(αβ)[n-1|n-1,l]ΦT+Q[n],

(24)

K[n]=P(αβ)[n|n-1,l]MT×

(MP(αβ)[n|n-1,l]MT+r[n])-1,

(25)

(26)

(27)

P(αβ)[n|n,l]=[Ip-K[n]M]P(αβ)[n|n-1,l],

(28)

(29)

其中，

(30)

r[n]=σ2。

(31)

(32)

值得注意的是，相較于傳統的卡爾曼濾波器模型，改進的卡爾曼濾波器的轉態轉換矩陣Φ不需要計算、更新自相關函數矩陣，因此具有較低的計算復雜度。此外，修正的卡爾曼濾波方法，不依賴于AR模型參數和自相關矩陣，因此不受最大多普勒頻率的限制，在用戶端高速運動時仍然有效。

2.2 基于AR模型信道預測

(33)

式中，a(αβ)[l]代表AR模型中第β個發射角度到第α個接收角度的第l個信道抽頭的參數，p代表AR模型階數。

以下計算AR模型的參數a(αβ)[l]，該參數可表示為：

(34)

根據Yule-Walker方程[13](Yule-Walker Equation)，a(αβ)[l]可以通過以下方程估計得到：

a(αβ)[l]=R(αβ)[l]-1v(αβ)[l]，

(35)

其中：

(36)

v(αβ)[l]=[R(αβ)[1,l]R(αβ)[2,l]…R(αβ)[p,l]]H，

(37)

利用上述計算所得參數，可以獲得式(33)中的信道預測。

3 仿真結果與分析

3.1 參數設定與預測誤差

在無線通信中，地面/近地MIMO信道主要由非視距 (NLOS)組成，因此本文主要考慮NLOS情況。使用QuaDRiGa生成信道數據并測試本文提出的預測模型。生成信道的系統參數匯總如表1所示。

表1 參數設定

對于實際的AWGN信道，定義AG-TD中信噪比(SNR)為:

(38)

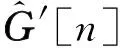
(39)

在此基礎上定義平均預測誤差為e0=E{e}。

3.2 仿真結果

為了測試提出的預測模型，利用CSI的時間和空間相關性來提高預測精度的能力，首先設置AR模型階數p=9，并用改進的卡爾曼濾波模型比較了該算法在4個信道表示域中的性能。圖3顯示了使用基于改進的卡爾曼濾波方法在4個信道表示域中的性能比較。從圖中可以看出，在實際的AWGN信道中，AG-TD預測精度高于其他3個預測域，這證明了本文提出的方法——基于改進的AG-TD卡爾曼濾波器模型——可以較好地利用信道狀態信息的空間相關性。因此，在接下來的仿真中，僅將提出的預測方法在AG-TD中與AR方法進行比較，以檢驗該模型利用CSI時間相關性的能力。

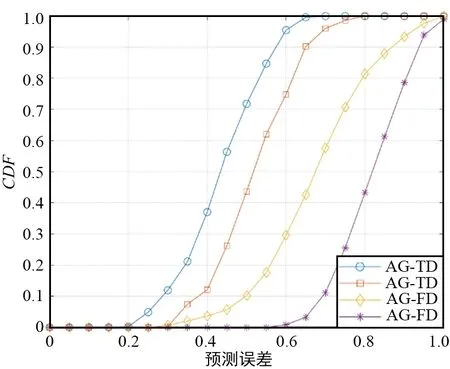
圖3 4個預測域的CDF曲線(SNR=20 dB,v=5 km/h)Fig.3 CDF Curve in four prediction domains (SNR=20 dB,v=5 km/h)

圖4顯示了移動速度為5 km/h、20 km/h時，本文提出的方法的平均預測誤差與信噪比函數與AR模型的對比關系。當信道功率明顯大于噪聲功率時，該方法具有與AR方法相似的性能。然而，隨著信噪比的降低，該模型的性能優于AR預測器，因此在實際無線有噪系統中具有更好的預測精度。此外，由于修正的卡爾曼濾波方法不依賴于AR系統參數和自相關矩陣，并不受限于最大多普勒頻率，因此該方法在高速運動環境下仍然是有用的。仿真結果表明，本文所提出的信道預測器有效利用了CSI時域的相關性，具有較高的預測精度。

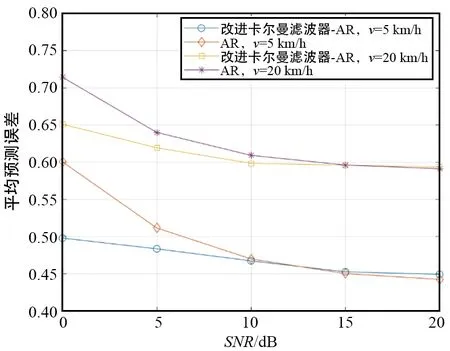
圖4 本文提出的改進的卡爾曼濾波器模型與AR模型的 平均誤差對比Fig.4 Average prediction error of proposed improved Kalman filter model and AR model

4 結論

本文利用信道狀態信息的空間和時間相關性，提出了一種適用于實際噪聲環境下的無線信道預測模型。該預測器為充分利用信道狀態信息的時間相關性，首先采用改進的卡爾曼濾波算法對基于上行探測導頻信道估計的信道增益矩陣進行修正，在此基礎上，本文提出利用AR模型在角度時延域進行信道預測，相較于其他域(天線頻率域、天線時間域、角度頻率域)，角度時延域信道具有較為明顯的信道稀疏性，有利于提高預測精度。仿真結果表明，在實際的AWGN信道預測中，該預測器的性能優于AR模型，這是因為通過改進的卡爾曼濾波器對CSI檢測值的校正，AR模型可以更好地利用CSI的時間相關性。在計算復雜度方面，為提高該方法在實際無線系統中的應用效率，本文采用改進的卡爾曼濾波器代替傳統的卡爾曼濾波器，降低了計算復雜度。通過基于改進的角度時延域卡爾曼濾波器的預測模型，可以充分利用CSI的空間和時間相關性，獲得較高的信道預測精度。