基于Radon變換和能量曲線的機織物密度檢測
彭 然 胡立文 鄧中民
(武漢紡織大學,湖北武漢,430200)
針對生產中機織物經密緯密測量以人工為主費時費力的問題,國內外不少專家學者提出了用計算機圖像處理技術來高效、簡化并準確地完成這項工作。前期大多數關于機織物經密緯密計算機自動測量研究采用的是快速傅里葉變換的方法。如利用傅里葉變換提取經紗緯紗的空間頻率信息測量織物密度[1];對織物圖像進行FFT變換求出頻譜,分析頻譜強度和分布,計算條紋分布和周期,從而得到經密緯密[2]。而后在傳統傅里葉變換的基礎上繼承和發展產生了小波變換。如用小波變換對機織物圖像進行多層離散小波分解和單層信號重構,分別求出重構后圖像沿經緯紗線方向的亮度平均值,根據亮度信號求出其周期,進而求出織物的經密緯密[3];研究了相關系數法在最佳重構層次選擇中的作用,提出預處理后進行小波變換,并運用數學形態學進行修正,最終平滑處理成條紋自動計數,計算經密緯密的方式[4]。
在進行實踐研究時發現,之前的研究方法存在可以改進的地方。一是圖像拍攝過程中織物傾斜導致因角度誤差帶來的精度影響使計算結果誤差大;二是小波處理時小波最佳分解級數的選擇基本是人為確定,需要反復試驗,并不能完全實現自動化。針對以上問題本研究提出了一種基于Randon變換和能量曲線,結合小波變換的圖像處理方法來實現機織物經密緯密的自動測量。
1 機織物圖像預處理
1.1 圖像采集
選擇10塊不同機織物,織物表面紋理清晰且干凈無污漬。采集圖像時盡量保持織物平整,采取固定的拍攝高度,且在織物的下方放置刻度尺。部分采集的織物圖像如圖1所示。

圖1 織物原圖
1.2 Radon變換校正
現今計算機圖像處理技術對于織物圖像的處理都是建立在織物必須是端正無傾斜的圖像前提下的,但是在織物圖像采集的過程中,由于拍攝環境、織物擺放、人為操作等因素總是無法避免拍攝的織物圖像出現傾斜的情況,而這樣會導致計算機處理無法獲得準確的織物經向緯向信息,造成最終織物密度計算結果誤差大。因此本研究采用Radon變換對織物圖像進行校正。
Radon算法是一種通過定方向投影疊加,找到最大投影值時角度,從而確定圖像傾斜角度的算法,如圖2所示。
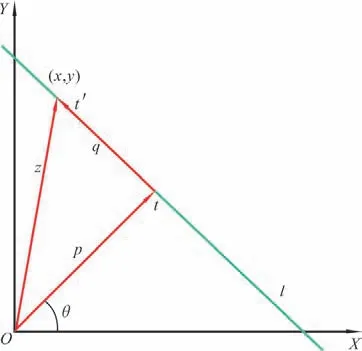
圖2 定義Radon變換的坐標系統
對f(x,y)的Radon變換Rf(p,θ)定義為沿p和θ定義的直線l的線積分。線積分公式見式(1)。
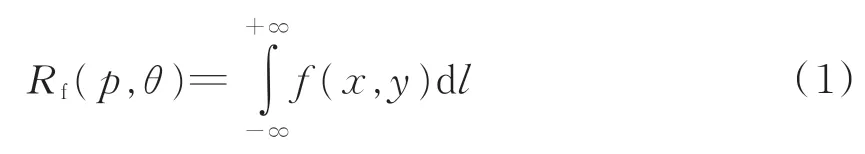
若函數f(x,y)表示一個未知的密度,對f(x,y)做Radon變換,相當于得到f(x,y)投影后的訊號,可以用Radon反變換投影后的結果,重建原始的密度函數f(x,y),它也是重建斷層掃描的數學理論基礎。
經Radon變換處理后,可以獲取織物傾斜角度,確定好傾斜角度后,經計算機程序將圖像自動旋轉相應角度,使得機織物經緯紗線保持橫平豎直,得到傾斜校正的織物圖像。經過Radon變換處理后圖像進行了3°的角度旋轉得到校正后圖像。截取大小為5 cm×5 cm的校正圖像保存用于后續處理,注意一定要截取織物部分,若拍攝部分取樣不足5 cm則盡量取10整除長度,便于后期經密緯密計算比較。
將校正圖像進行預處理轉換為灰度圖像,再進行平滑去噪處理,并用直方圖規范化增加圖像對比度,使織物經緯紗線信息更加清晰突出。
2 小波變換處理
2.1 小波變換
小波變換可將二維圖像逐層分解得到原圖像的低頻、垂直高頻、水平高頻和對角線高頻分解圖像[5-9]。低頻部分可以繼續分解,這個過程能一直持續下去;在某一層的垂直高頻重構圖和水平高頻重構圖中機織物圖像的經紗與緯紗信息將得到最佳保留。小波一級及三級分解圖如圖3所示。
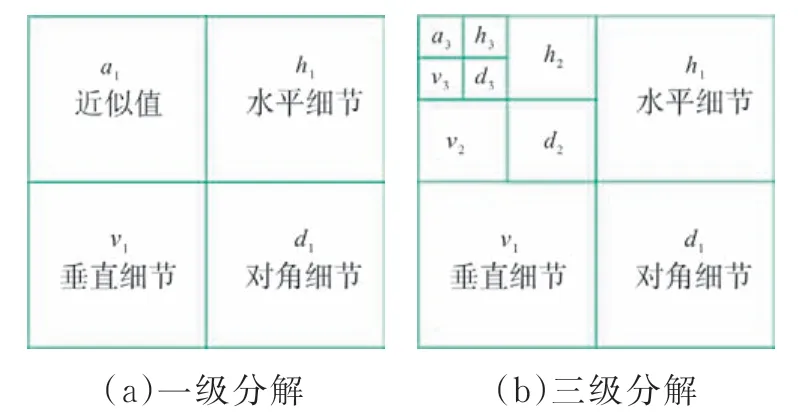
圖3 小波一級及三級分解圖
機織物是由經紗和緯紗垂直交織而成,圖像小波分解得到水平分量和垂直分量基本類似于織物的經向緯向信息,通過處理得到的水平垂直分量即可計算織物的經密緯密。
2.2 能量曲線確定最優分解級數
試驗采用wavedec2函數對圖像進行多尺度二維小波變換處理,選定小波基函數bio5.5,用該小波對二維信號X(即織物圖像)進行N(N=7)層分解,每一層分解分別得到近似分量、水平細節分量、垂直細節分量和對角細節分量。在對織物圖像使用小波進行不同層次的分解,得到的水平分量和垂直分量信息完全不同,分量與經緯紗線數目的匹配程度也完全不同。因此小波分解的分解級數直接影響得到的水平垂直分量的數量,也直接影響了圖像反映的織物經密緯密準確性,在圖像處理的實際操作中需要選擇合適的分解級數以得到與經緯紗線圖像高度匹配的經紗、緯紗根數信息。同一織物不同層數處理結果如圖4所示。

圖4 同一織物不同層數處理結果
由圖4可以看出,同一織物在同樣的處理過程中采用不同的分解級數下得到的分量各不相同,對圖中不同層數處理下的分量結果進行計算,在N=3時經密緯密計算結果最為準確,得到分解級數N=3是該織物的最優分解級數。根據對大量織物圖片進行不同分解級數處理試驗,發現每一塊織物都存在一個最優分解級數,并且該最優分解級數與小波變換處理得到的各分量之間存在一定的關系。
由此在確定最佳分解層數時引入能量曲線的概念。即將織物圖片小波分解后每層的分量利用w energy函數,采用小波系數平方,然后求和,計算得到各分量的能量占比,最后再歸一化,繪制其能量比值曲線。
設定織物圖像經N層分解后的近似分量的能量為Es,分解后每層細節分量(包含水平細節分量、垂直細節分量和對角細節分量)的能量為Ed,能量計算公式見式(2)。
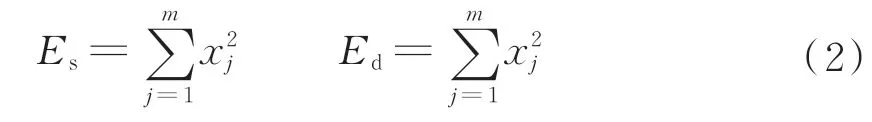
式中:m表示分解后該分量的數據個數,xj表示分解后的每個分量包含的數據(j=1,2,…,m)。經過i層(i=1,2,…,N)分解后的總能量Ez,見式(3)。求出分量的能量占比Di,見式(4)。織物處理后繪制的能量曲線如圖5所示。
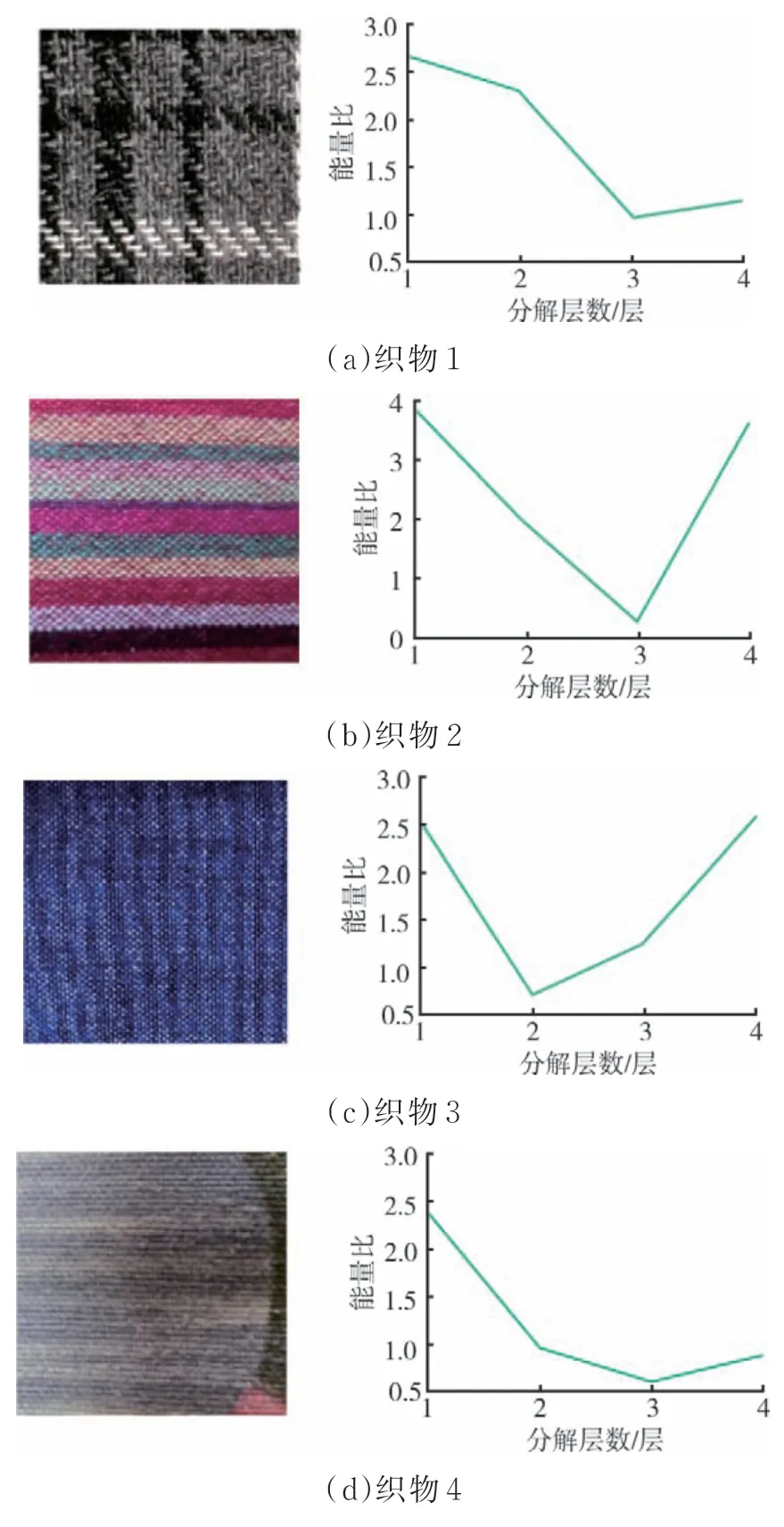
圖5 不同織物繪制的能量曲線圖
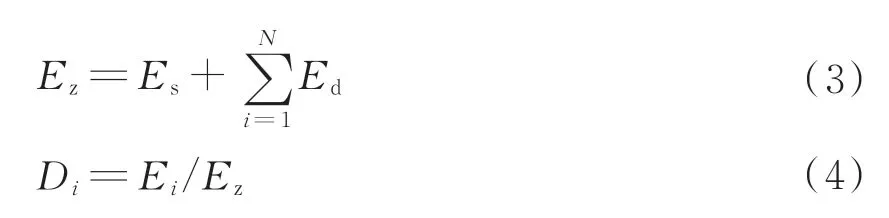
從圖5中發現每個能量曲線確實都存在一個最小峰值,為了確定能量曲線的最小峰值是否和小波處理需要的最優分解級數一致,進行了大量的試驗比對,最終確定能量曲線最小峰值可以作為織物圖像小波分解最優分解級數值來使用。
選取能量曲線最小峰值對織物圖像進行小波分解和重構,得到經密緯密計算需要的織物垂直分量圖和水平分量圖。
2.3 織物重構圖優化
小波分解與重構后的垂直分量和水平分量呈現出波浪狀,并不能很好表示織物紗線根數信息,這樣無法準確計算織物密度,必須進行進一步的處理。不同織物小波處理結果如圖6所示。其中,左圖為垂直抖動法圖像,右圖為水平抖動法圖像。

圖6 不同織物小波處理結果圖
本研究采用誤差擴散抖動法來實現圖像的二值化處理,對重構后的垂直分量和水平分量進行二值化,得到的圖像產生黑白交替的像素,且與原來的灰度看起來很接近,既保護了邊界,又減少了計算量。
二值化后圖像的黑白交替像素排列雖然能看出紗線的排列情況,但不光滑,還含有噪聲,且不方便計數,要進行平滑處理。平滑處理的原理是以圖像中處于多數的灰度值(0或1)代表這一行或列的具體形態(黑或白),使紗線變直,達到平滑的效果,以方便計算紗線數量[10]。處理結果如圖7所示。

圖7 各織物分量優化效果
3 機織物經密緯密計算
經過優化處理后得到的水平分量和垂直分量圖像,就是與織物高度匹配的經紗緯紗排列,取優化后圖像的行或列,計算連續黑色像素的個數除以圖像長度(寬度),得到該方向的紗線排列密度(根/像素),根據電腦分辨率(像素/cm)即可計算出機織物密度(根/10 cm)=紗線排列密度×分辨率×10。
運用此程序對選取的10塊布樣進行測試,并使用照布鏡對每塊織物進行經密緯密的人工測量,每塊織物測得3個數據,然后取其算術平均值為最后人工的測定結果。將測試結果與傳統的人工測試進行誤差計算。數據比較見表1。
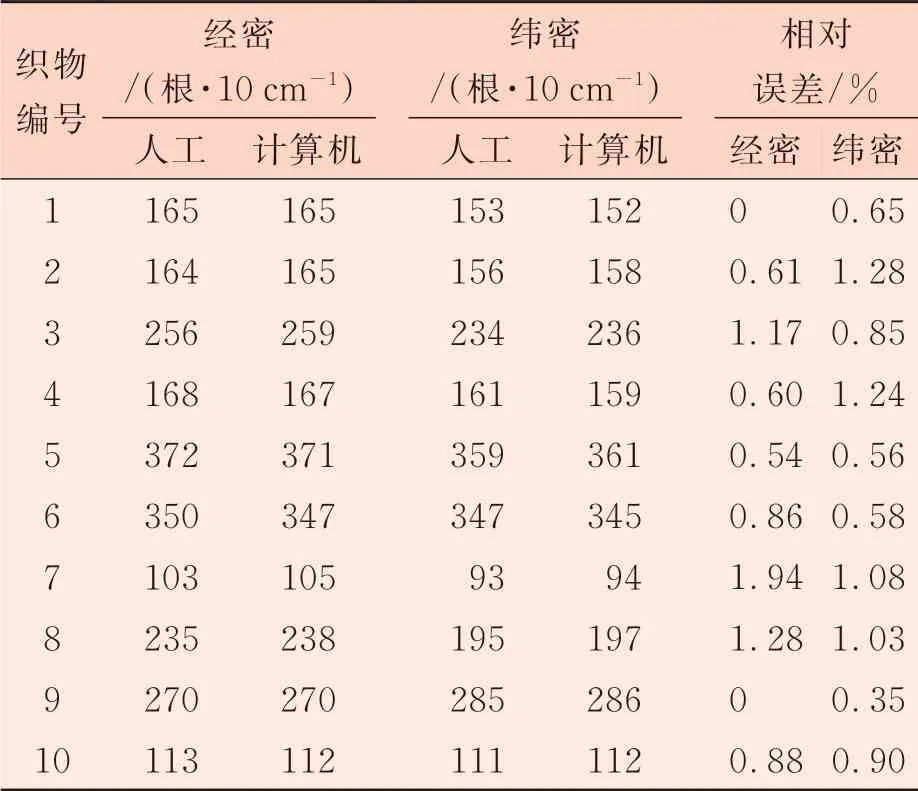
表1 人工測量和計算機測量的數據比較
由表1數據可以看出,計算機程序處理得到的結果和人工測量結果基本一致,織物經密緯密檢測的相對誤差在1.00%左右,結果較為理想。
4 結語
用計算機圖像處理方法測試機織物的經密緯密,相比于傳統人工測試處理速度快、效率高、勞動強度小,且計算結果也基本準確。Radon變換校正較好地解決了織物傾斜的問題,能量曲線確定最優分解級數方法的提出,進一步滿足了自動準確測量經密緯密的需求,但也有不足之處。試驗中發現在處理組織結構復雜的織物,例如多種彩色細條花紋織物、有裝飾性花樣設計的織物,相對于結構簡單或是素色織物來說處理結果不夠準確,還需要進一步研究改進。

