基于多元回歸的危化品道路運輸事故風險影響因素分析

劉子暄

（北京化工大學，北京 100029）

隨著我國經濟的迅猛發展，現代工業化程度不斷提升，使用的危化品數量和種類也越來越多，隨之而來的是危化品的道路運輸安全問題，一旦危化品的運輸車輛在公路上出現意外，事故造成的影響范圍會比較廣[1]。如：2014年7月19日，在滬昆高速公路湖南邵陽范圍，一輛滿載乙醇的貨運卡車，因司機長時間疲勞駕駛，發生與客車相撞的重大交通事故，造成54人死亡，直接經濟損失達0.53億元；2015年8月，在廣東沈海高速陸豐龍山方向，一輛滿載NH4NO2的貨運卡車與載人客車發生追尾事故，造成6人當場死亡，30余人受傷；2016年3月，一輛滿載汽油的貨運罐車在京港澳高速何家壟段，因車輛故障發生爆炸事故，導致現場6人死亡。這些惡劣的交通事故給國家和群眾帶來巨大的經濟損失和社會影響[2]，所以必須有效控制危化品的運輸安全。

因此如何高效辨識和分析交通事故風險是當前交通運輸安全領域重要研究熱點方向，潘福全、孟亞然、馬昌喜，等[3]對危險化學品道路安全運輸特點進行了總結歸納，并對我國目前交通安全運輸相關研究現狀作出了分析；高潔[4]采用綜合評價的方法對危化品道路運輸安全評價指標進行了構建；閆利勇[5]對危化品公路運輸特點以及相應的應對措施進行了總結；吳宗之[6]針對以往危化品運輸事故，以發生時間、地點等因素為出發點進行了總結；張麗[7]等對我國2006到2007年發生的危險化學品道路運輸事故進行了分析和總結；辛春林[8]等對以往發生的危化品道路運輸事故現場數據進行了系統分析。

Logistic回歸從定義來說，屬于一種廣義線性回歸，所以和多重線性回歸分析進行對比，二者有很多的相同之處。在模型形式方面，二者具有基本相同的特點，均具有 w‘x+b，其中w和b均作為待求參數，二者的區別僅僅是在其因變量不同，其中多重線性回歸的因變量是w‘x+b，即y=w‘x+b，而logistic回歸則是利用函數L，將一個隱狀態p與w‘x+b進行對應，即p=L(w‘x+b)，然后根據1-p和p的數值大小再決定因變量的值。如果L是logistic函數，那此回歸就是logistic回歸，如果L是多項式函數，那此函數就是多項式回歸。

基于以上內容，本文結合危化品道路運輸事故影響因素及logistic回歸的優勢，利用危險化學品道路運輸安全事故影響因素來建立數據耦合度量模型，從而將該模型下危險化學品道路運輸安全事件發生的概率和風險值進行計算，為危化品道路運輸安全風險預防和控制管理提供理論依據。

1 指標的選取

通過文獻研究，在因果鏈理論的基礎上，人們通過誤差理論和軌跡交叉理論參照前面選取的指標對事故原因進行分析，我們可以閱讀針對爆炸事故的調查報告，根據相應的專家知識，將事故的產生原因劃分為以下幾個方面，即：人為因素、環境因素、物質因素以及管理因素。

人為因素包括駕駛員的精神狀態（是否有疲勞駕駛）、駕駛員的操作（駕駛過程中是否有不當操作）。這些因素包括危險化學品的類別、運輸設備的狀態和車輛的運行狀態。環境因素包括時間劃分、月份劃分、道路類型和天氣條件。管理因素包括公司資質、駕駛員資質和車輛資質。每個指標的值如表1所示。

表1 指標選取

2 相關性分析

本節運用SPSS軟件通過二元相關性分析及交叉表分析，對本章構建的指標體系進行相關性分析。

2.1 二元相關性分析

在進行相關分析之前，建議使用散點圖來可視化數據之間的關系。判斷是否有關系（如果有*，則有關系；否則，沒有關系）；然后判斷相關為正相關或負相關（相關系數大于0為正相關，反之亦然）。最后判斷關系的親密程度（通常相關系數大于0.4表示關系親密）。

由表2可知，精神狀態與操作失誤相關性顯著關系緊密。

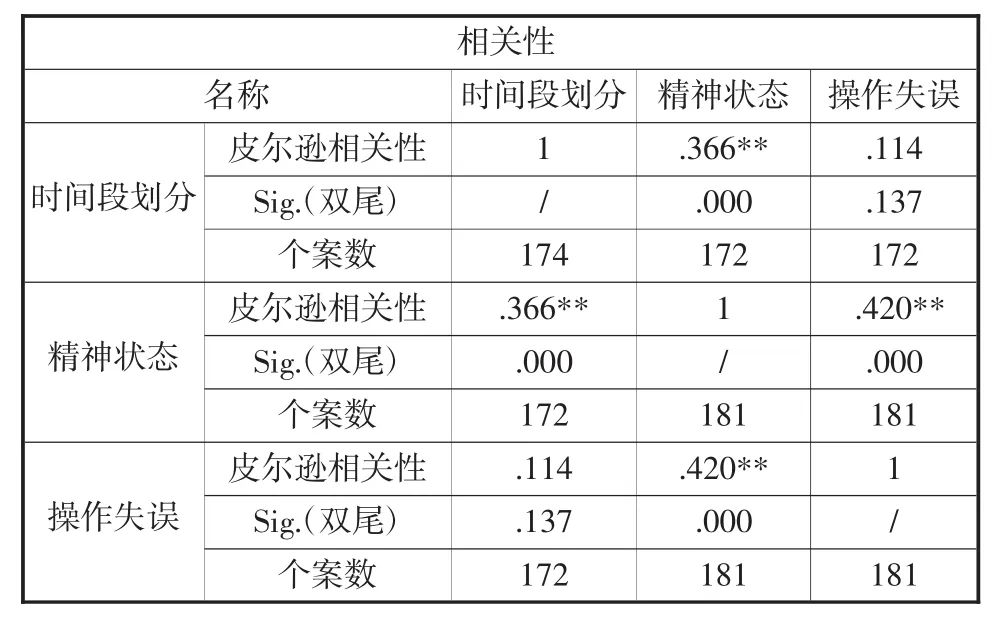
表2 精神狀態和操作失誤相關性

由表3可知，運輸資質與所屬公司資質相關性顯著關系極其緊密。

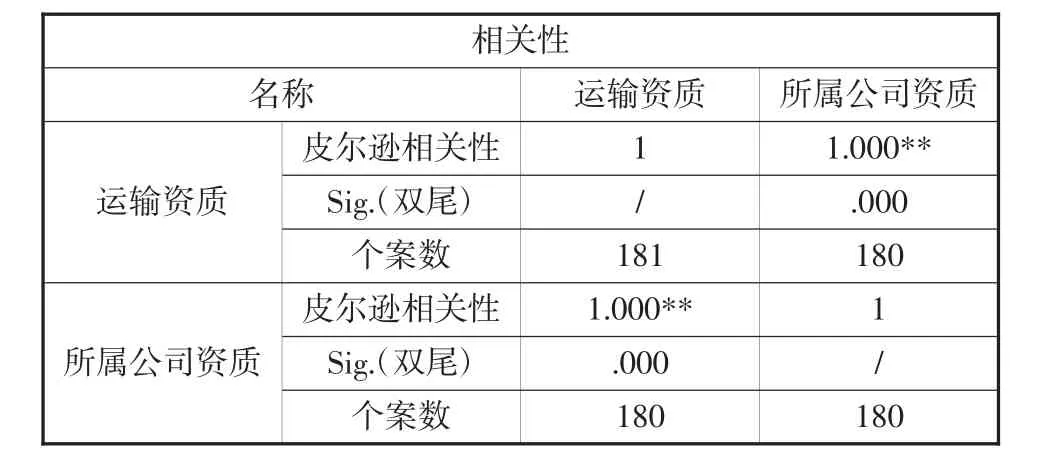
表3 運輸資質與所屬公司資質相關性

由表4可知，運輸車輛是否合規與所屬公司資質相關性顯著關系極其緊密。

表4 運輸車輛是否合規與所屬公司資質相關性

由表5可知，運輸車輛是否合規與設備狀態相關性顯著關系緊密。

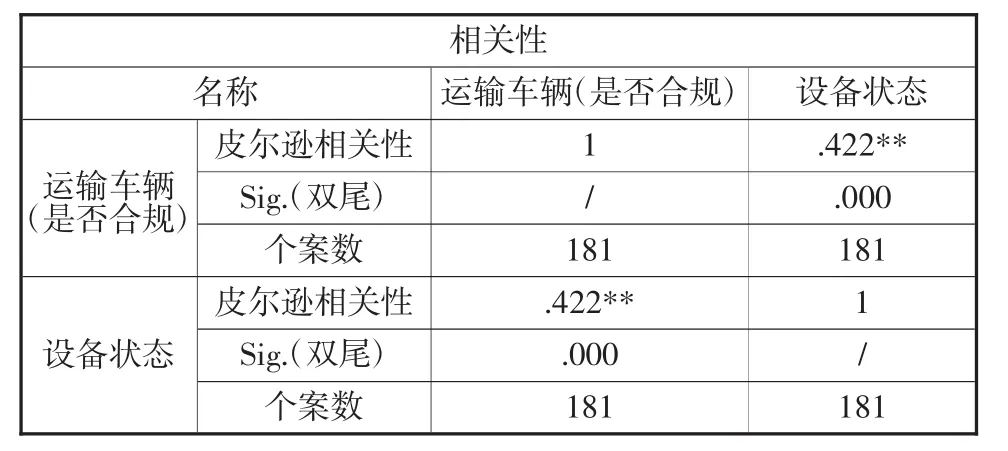
表5 運輸車輛是否合規與設備狀態相關性

2.2 二元logistic回歸分析

2.2.1 模型系數的綜合測試

模型的一行輸出logistic回歸模型中，所有參數是否為0的似然比檢驗結果。P<0.05指的是擬合模型中至少一個變量的OR值具有統計顯著性，即模型具有總體顯著性。

2.2.2 霍斯默-萊梅肖檢驗

指測試模型的擬合度。如果P值大于測試水平（即P>0.05），那么則可表明已經完全提取出當前的信息內容，并且模型擬合的優度高。

2.2.3 方程中的變量

a）本統計過程中變量的篩選方法是正向的LR法。方程表中的變量列出了最終過濾到模型中的變量及其參數。其中，sigg.a列表示模型中P值（對應變量的），Exp(B)和Exp(B)的95%CI表示模型中對應變量的OR值及其95%置信區間。

b）對于含有多類別變量的模型，在計算設置中設置“0”組作為其參考值，當測試結果是“1”組和“2”組時，計算結果分別對應于“0”組的OR值。在logistic回歸中，具有虛擬變量的若干個分類變量均具備同樣的In值和Out值，也就是說，相對于參照組，只要出現一組具有統計顯著性變量，則與該變量相關的所有組均會被納入計算模型中。在變量的第一行并不具有OR值，其P值指的是變量整體檢驗具有差異性，并存在一定的統計學意義（即至少有一組相對于參照組有統計學意義或值）。

c）本研究中的變量以“0”組為參照，因此“1”相對于“0”組的OR值和P值在第（1）行的參數中給出，而“2”相對于“0”組的OR值和P值在第（2）行的參數中給出。常數是回歸方程的截距，在模型中一般沒有實際意義，所以沒有必要去注意它。

部分分析結果見表6～表12。

傷亡情況——品類+時間段+天氣狀況+事故責任（見表6～表8）。

表6 模型系數的Omnibus檢驗（品類+時間段+天氣狀況+事故責任）

表7 霍斯默-萊梅肖檢驗（品類+時間段+天氣狀況+事故責任）

表8 模型摘要（品類+時間段+天氣狀況+事故責任）

傷亡情況——品類+事故類型+危化品狀態+事故責任方（見表9～表12）。

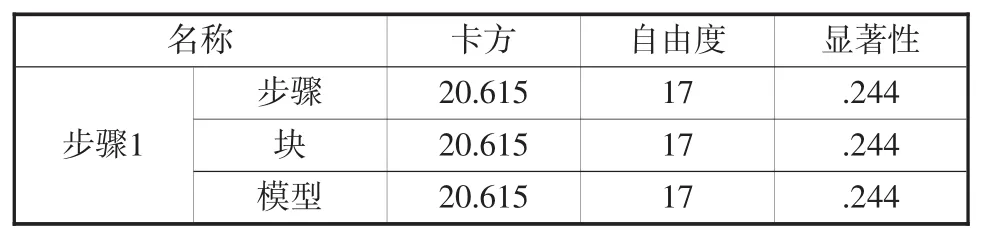
表9 模型系數的Omnibus檢驗（品類+事故類型+危化品狀態+事故責任方）

表10 模型摘要（品類+事故類型+危化品狀態+事故責任方）

表11 霍斯默-萊梅肖檢驗（品類+事故類型+危化品狀態+事故責任方）

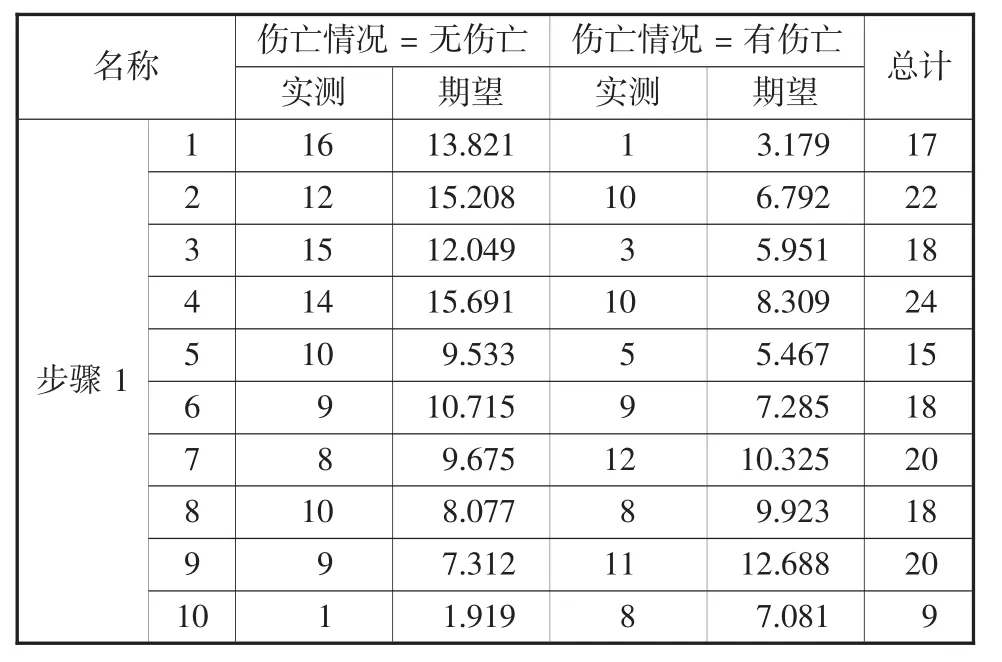
表12 霍斯默-萊梅肖檢驗的列聯表

2.3 多元logistic回歸分析

部分分析結果見表13～表22。

傷亡人數合計劃分——時間段+道路類型+天氣狀況（見表13～表17）。

表13 模型擬合信息（傷亡人數合計劃分）

表14 擬合優度（傷亡人數合計劃分）

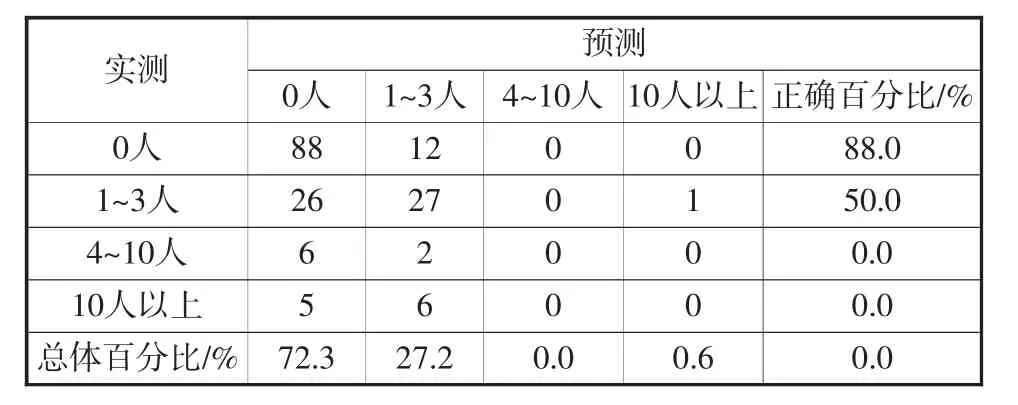
表15 分類（傷亡人數合計劃分）

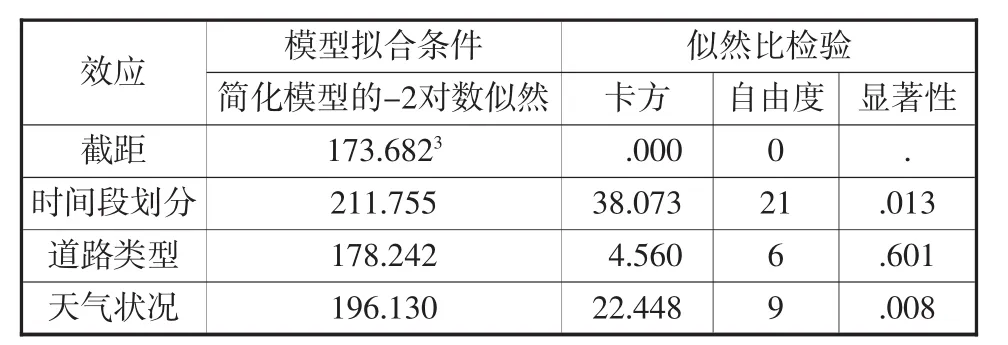
表16 似然比檢驗（傷亡人數合計劃分）

表17 偽R方（傷亡人數合計劃分）

傷亡人數——精神狀態+運輸車輛+設備狀態+行駛狀態（見表18～表22）。

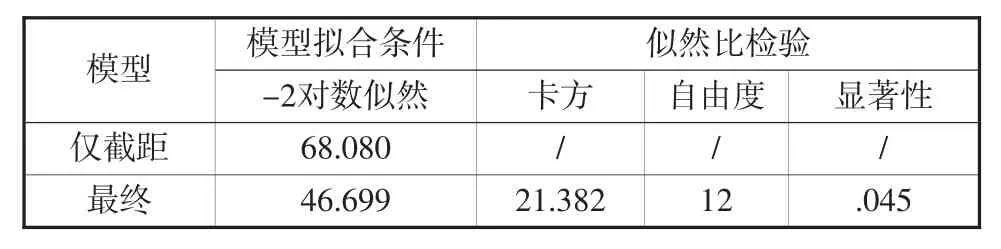
表18 模型擬合信息（傷亡人數）

表19 擬合優度（傷亡人數）

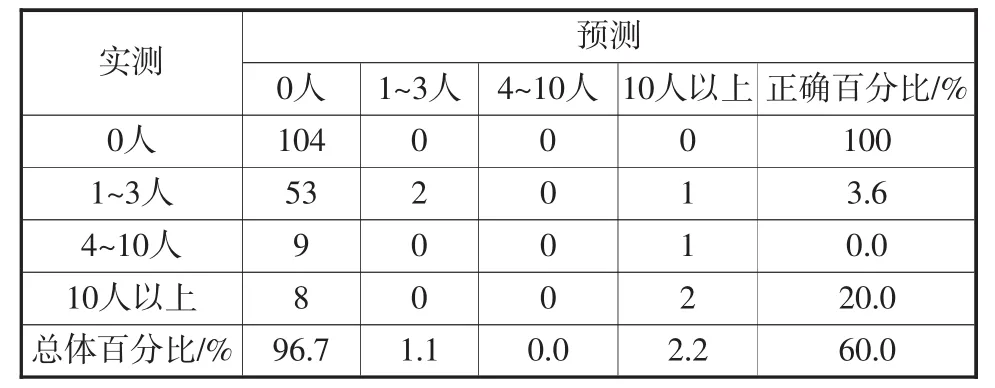
表20 分類（傷亡人數）

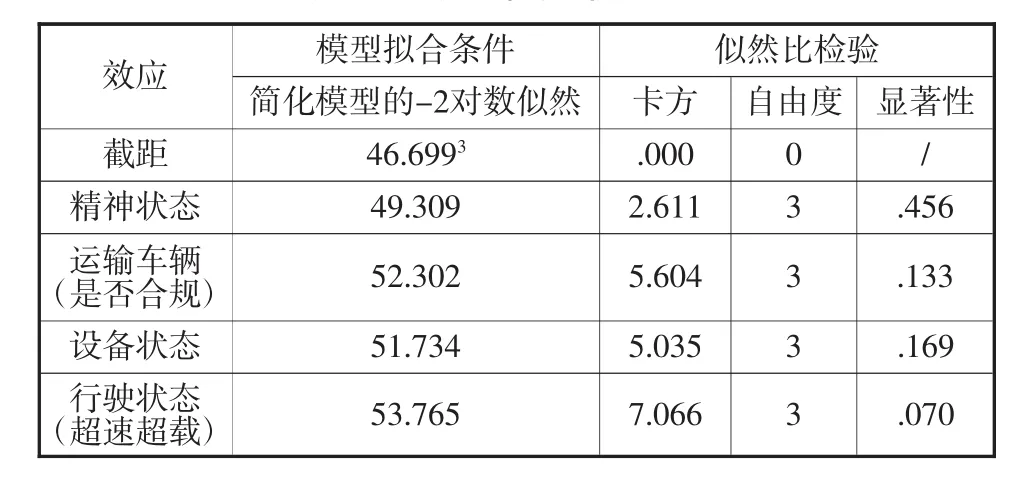
表21 似然比檢驗（傷亡人數）

表22 偽R方（傷亡人數）

3 綜合分析

由以上各因素之間的相關性分析可知，運輸車輛是否合規以及司機是否具有運輸資質與所屬運輸公司是否具有資質且合法合規運營具有極大的相關性；司機在事故發生時是否有操作失誤情況與司機的精神狀態有緊密相關性；危化品類型與事故后危化品狀態有極為顯著的相關性關系；事故類型與事故責任方有極為顯著相關性；事故類型與事故后危化品狀態有極為顯著相關性關系；周邊環境狀況與事故后危化品狀態有顯著相關性。根據分析篩選，對于危化品道路運輸事故有較大關聯的因素分別為月、時間段、道路類型、品類劃分、天氣狀況、精神狀態、操作失誤、危化品狀態、事故類型、事故責任方。