基于交通流數據修復的GA-RF方法研究

邵毅明，甘元藝，侯雨彤，鐘 穎

（重慶交通大學 交通運輸學院，重慶 400074）

準確、可靠的交通流預測信息可以直接應用于先進的交通管理系統和信息服務系統，為出行者提供實時有效的交通運行信息［1］。同時，可靠的交通流預測是交通管理部門采取交通控制和誘導措施的重要依據。通過對短時交通流的預測，可以提前調整交通管理控制手段，從而提高交通運行效率［2－4］。交通流數據是時間序列數據，數據質量直接影響交通流預測結果的精度。在實際道路交通系統中，由于檢測設備、傳輸設備等出現故障的原因，使采集的交通流數據或多或少存在缺失［5－6］。雖然缺失數據的數量隨著信息技術的發展有逐漸變少的趨勢，但是為了保證交通流預測結果的準確性，在少量數據缺失的情況下，依然有必要對交通流數據修復方法進行研究。

目前，交通流缺失數據時間相關性修復方法多是采用歷史均值法、歷史相鄰加權法以及預測修復3種［7］。歷史均值法采用前n天當前時間點的對應數據均值并填充［8］，歷史相鄰加權法獲取前一天同一時刻的歷史數據和當天前一時刻的實測值進行加權平均來修復缺失數據［9］。歷史均值法、歷史相鄰加權法屬于基于歷史數據的缺失數據修復，這兩類方法簡單易行，能夠解決時間序列修復對連續異常數據修復能力不足的問題，但存在不能反映交通流真實變化的情況。交通流數據從本質上而言屬于時間序列數據，所以基于時間序列的各種缺失值修復方法都適合交通流缺失數據的修復，預測修復就是典型［10］。預測修復主要將待修復變量作為目標變量，與其相關的變量作為特征向量，構建預測模型，實現對缺失數據的預測修復。已有研究采用RBF神經網絡方法［10］、LSSVM的組合閾值修復方法［11］、SVR方法［12］、偏最小二乘法［13］等進行預測修復。

RF集成了bagging和隨機選擇特征分裂等方法的特點，不僅對噪聲和異常值具有較好的容忍度，且相較于AdaBoost、SVM等方法，具有運行速度快、精度高、參數調節方便等優點，現階段RF算法主要應用于交通流預測方面，有學者通過實例驗證了RF預測城市短時交通流具有合理性和高效性［14－15］。RF預測結果與模型參數的優化密切相關，當前研究多是探討RF模型在預測中的應用，未探索優化方式。GA是通過模擬生物在自然環境中的遺傳和進化過程形成的自適應全局優化搜索算法，可用于不同領域的參數尋優、路徑規劃等［16］。結合以上情況，在考慮交通流時間序列相關性的基礎上利用優化的RF算法對存在少量數據缺失的交通流數據修復進行研究：用GA優化RF模型的重要參數，以修復誤差最小為主要目標，提出GA-RF的交通流缺失數據修復方法。采用重慶市南岸區某路段的交通流數據進行模型實證，并與其他數據修復方法進行對比，結果顯示GA-RF模型在少量交通流數據缺失情況下，修復誤差低于歷史均值法及歷史相鄰加權法，修復精度更高，具有更好的修復性能。

1 隨機森林算法

RF模型簡單、容易實現、計算開銷小，被譽為“代表集成學習技術水平的方法”［17］，能同時解決分類與回歸問題。RF的“森林”體現在模型是由一定數量的決策樹構成，而“隨機”則體現在樣本的隨機性和特征的隨機性。設訓練數據組共有N條數據，要構建的決策樹個數，即森林的大小為M，每個數據點有P維特征，則RF的執行過程如圖1所示。

圖1 隨機森林算法示意圖

其中，training＿data為N行P列的樣本數據集，從該樣本集中有放回采樣M次形成M個不完全相同的子數據集bootstrap（i），分別在M個子數據上訓練單一決策樹模型，形成含有M棵樹的“森林”，給定一個新的待識別對象，隨機森林中每一棵樹會根據該對象的屬性給出各自的預測結果，最后依據每一棵樹的預測結果得出整個隨機森林的預測結果。而根據問題類型的不同，給出的結果或為離散值，或為連續值。當結果為離散值時，表明當前問題為分類問題，遵從“少數服從多數”原則，采用投票法決定最終預測類別；反之，當為連續值時，表明為回歸問題，則通過對各單一決策樹的預測結果進行加權平均得到最終的預測值。隨機森林是一種非線性建模工具，精度高且具備一定的容忍度，不易出現過擬合［18］。

2 交通流缺失值修復的GA-RF模型

RF模型含有許多重要參數，參數的不同取值組合可以產生不一樣的結果。為得到更好的預測精確度，需對模型的重要參數進行調參操作。現有的學習曲線調參步驟復雜、訓練時間長，因此提出GA-RF模型，在搜索空間內利用GA算法對RF模型的重要參數尋優，使RF的調參過程更加高效、便捷。

2.1 模型預測修復流程

GA-RF交通流缺失值修復模型的修復流程如圖2所示，包括數據處理模塊、參數調優模塊和預測修復模塊。

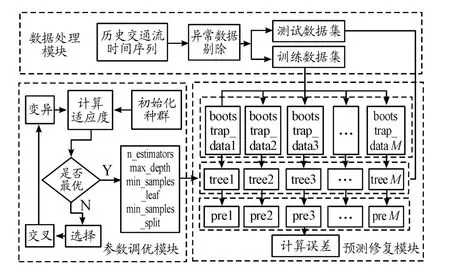
圖2 基于GA-RF模型的交通流缺失值修復框架圖

首先，數據處理模塊先剔除異常數據，用剔除異常數據后的歷史交通流數據構造樣本訓練集及測試集；然后參數調優模塊采用遺傳算法對RF中樹模型的數量（n＿estimators）、最大深度（max＿depth）、節點分支后每個子節點最少包含的訓練樣本（min＿sample＿leaf）、1個節點能進行分支的最少訓練樣本（min＿samples＿split）4個參數在搜索空間進行優化，確定參數的最佳組合；預測修復模塊利用構造好的訓練集以及尋優后的參數組合對RF模型進行訓練，形成GA-RF模型，最后將測試數據輸入GA-RF模型中進行預測修復，對修復值與真實值進行誤差分析并輸出。

2.2 訓練集及測試集的構造

基于隨機森林算法對交通流缺失數據進行修復的基本原理為：將剔除異常數據后的歷史交通流數據分為樣本訓練集及測試集，利用訓練集數據訓練模型，測試集數據判斷模型預測精度；然后將路段的真實待修復數據集中的缺失數據列作為待預測對象，利用訓練好的模型對其進行預測修復。假設目標路段在某段時間內的平均速度的數據集為X＿data，觀測時間間隔為5 min，X＿data共有M行，每行有N維特征，則數據集X＿data可表示為：

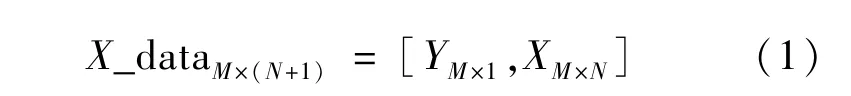
式中：Y為目標變量標簽列，X為Y的特征向量矩陣，從交通流時間序列相關性出發構造特征向量，即令xt為t時刻目標路段交通流，xt－n為t時刻前第n個時刻的交通流，則交通流時間序列相關性可表示為：

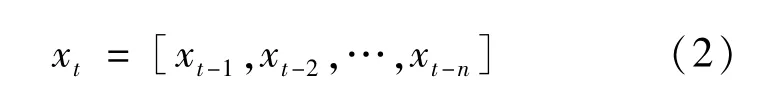
式（2）表明，當前時刻路段交通流與其前n個時段交通流相關，其中xt相當于式（1）中的目標變量標簽列Y，xt－1至xt－n則相當于式（1）中的特征向量X，則從初始時刻到t時刻，樣本數據集中的特征向量矩陣X如式（3）所示，目標向量Y如式（4）所示：

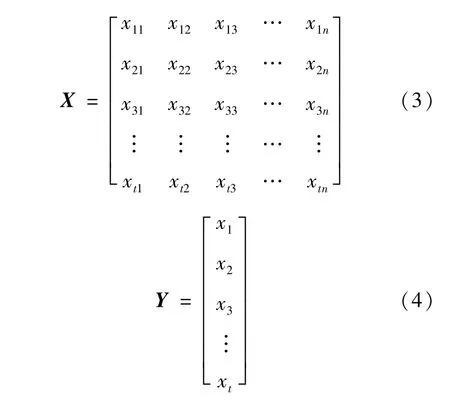
由于交通流時間序列數據存在缺失值，因此，考慮時間序列相關性構造的特征向量也存在缺失數據，而用于模型訓練的數據應是完整數據集，故從構建好的X＿data數據集中提取各特征均不包含nan值的數據行特征集合作為最終的訓練集，按一定比例將其劃分為訓練數據集（X＿train，Y＿train）、驗證集（X＿val，Y＿val），其中訓練數據集用于模型的訓練，驗證集則用于模型的調參。為明確模型的修復精度，選擇交通流數據較為完整的某天數據作為測試集，人為隨機構造缺失值，利用訓練好的模型對缺失數據進行預測修復，比較修復值與真實值的誤差，對模型預測修復精度進行評價。最后，提取Y為nan的數據行作為路段的真實待修復數據集合，利用構建好的GA-RF模型修復路段交通流中的缺失數據。

2.3 參數調優

RF的重要參數及其含義如表1所示。

表1 隨機森林模型重要參數

以平均絕對誤差（MAE）作為評價指標，參數調優過程就是通過不斷迭代，尋求以上4個重要參數的最佳組合，使基于該參數組合的模型具有最低的MAE。整個過程是一個全局尋優問題，在眾多參數組合中尋找最優參數組合。

遺傳算法是通過模擬生物在自然環境中的遺傳和進化過程形成的自適應全局優化搜索算法，可用于不同領域的參數尋優、路徑規劃等，其運算過程主要包含初始種群的產生、個體適應度的計算、根據適應度值對種群中的個體進行選擇、交叉以及變異、產生新種群，以此循環，迭代直至滿足條件后終止［19－20］。GA優化RF主要采用GA對RF模型參數進行尋優，使模型預測性能在一定程度上達到最優。采用GA對RF的n＿estimators、max＿depth、min＿samples＿leaf、min＿samples＿split進行調優，獲取搜索空間的最優參數組合，構成GARF模型。參數調優具體步驟如下：①種群初始化并進行編碼；②將RF模型的MAE作為適應度函數；③將解的個體進行選擇交叉變異操作，進行解碼；④獲得適應度目標值和最佳參數；⑤計算基于最佳參數的MAE；⑥終止條件判斷，若未達到迭代次數，則返回③繼續計算；若達到迭代次數，則停止計算，輸出調優參數的最佳組合。

2.4 缺失值預測修復

GA-RF數據修復方法的最后一步為利用構造好的訓練集（X＿train，Y＿train）以及尋優后的參數組合對GA-RF模型進行訓練，然后利用訓練好的模型對缺失數據測試集進行預測修復，選定評價指標對修復結果進行評價。設時間窗窗口長度為5，即假定待修復時刻交通流與其前5個時刻的交通流數據相關，則待修復缺失數據集數據結構如表2所示。

如表2所示，某時段內存在待修復缺失數據，取缺失數據所在時刻的前5個時刻的平均速度數據作為特征矩陣，對缺失數據進行預測修復。由于5個特征向量是由目標變量標簽列衍生的，故特征向量中也存在缺失值，且該缺失值來自于當前待修復時刻的先前時刻。因此，只要第1個缺失數據的前5個數據不存在nan，即可通過構造特征向量、提取待修復缺失數據、預測修復的循環操作實現對缺失數據的全部填充，缺失數據修復具體步驟如下：

表2 待修復缺失數據集數據結構

步驟1 考慮交通流時間序列相關性對含缺失數據的M個交通流數據進行N維特征向量提取，形成M行N＋1列數據矩陣row＿data；

步驟2提取row＿data中標簽列為nan的數據行，構成待修復缺失數據集missing＿data；

步驟3判斷第1個缺失數據所有特征列是否含有nan，有轉步驟4，無則轉步驟5；

步驟4采用缺失值所在時段的均值對nan進行修復，并實時更新row＿data；

步驟5 提取missing＿data中特征列完整的數據行，調用構建好的模型對缺失數據進行預測修復，并用修復后的缺失數據實時更新row＿data中對應的缺失數據，然后轉回步驟2，反復進行，直至missing＿data行數等于0，則所有缺失數據修復完畢。

3 GA-RF模型實證

為了驗證所提出的GA-RF模型的可行性，選用重慶市南岸區某路段的交通流數據展開GA-RF模型實證：在測試數據集中隨機構造少量缺失數據，以MAE為主要評價指標，均方根誤差（RMSE）、均方誤差（MSE）、平均絕對百分比誤差（MAPE）評價指標作為輔助，以主要評價指標最小為目標，對缺失數據修復的有效性進行評價，并在同等缺失比例下將GA-RF的修復效果與RF方法、歷史均值法及歷史相鄰加權法修復效果進行對比實驗。

3.1 實驗環境

全部代碼均通過Python程序語言實現，Anacond包中的spyder4.1.3版本作為集成開發環境，Windows 10（64位）操作系統、Intel（R）Core（TM）i5－10210U CPU＠2.11 GHz處理器、16GB內存等作為硬件支撐平臺。

3.2 實驗數據處理

以重慶市南岸區某路段的歷史交通流平均速度數據作為實驗數據，用于GA-RF的交通流缺失數據修復實驗。實驗采集了該路段從2018.07.21—2019.06.26的交通流平均速度，由于本次研究只針對工作日，故提取數據集中的工作日數據，構建從0∶00－24∶00、以5 min為增長梯度的完整時間序列。數據集的平均速度分布如圖3所示，橫坐標表示時段分布，縱坐標表示該時段的平均速度，圖中數據集應包含62 784個交通流數據，對數據集進行分析，部分數據存在缺失和異常。

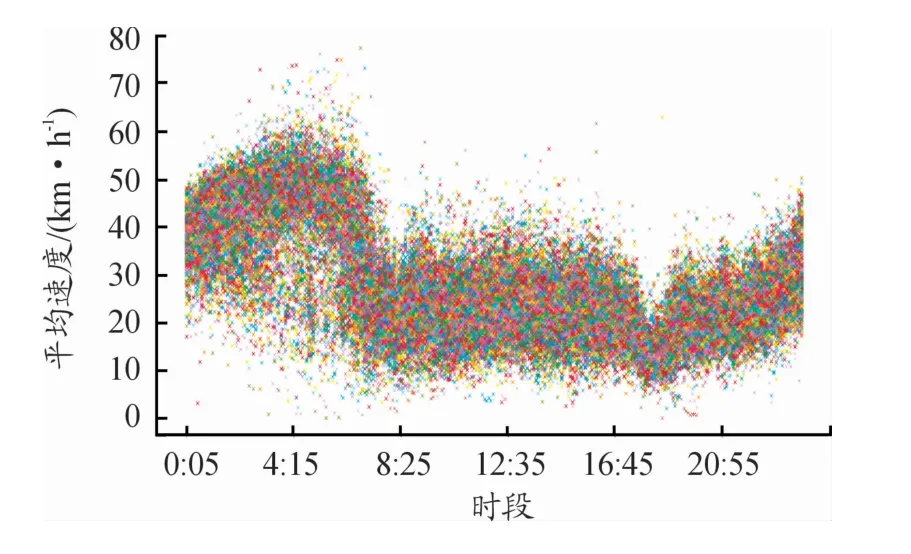
圖3 數據集平均速度分布

將構造后的時間序列與原始時間序列進行笛卡爾積，挖掘原始樣本中的缺失數據，共計1 284條，并以nan進行標識，則以天為計量單位的路段交通流缺失數據分布情況如圖4所示。

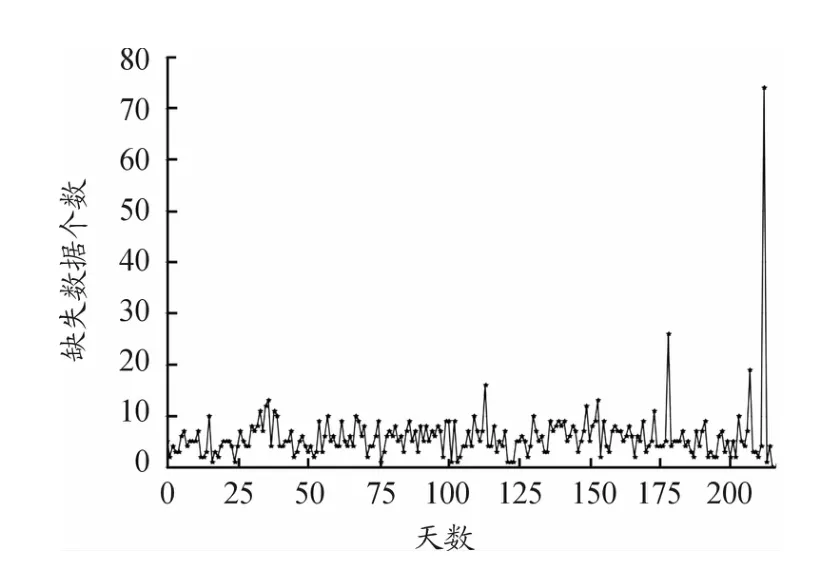
圖4 以天為計量單位的缺失數據分布

異常值分析是保證數據質量的前提，找出數據的異常值，有利于最終得出的模型的穩定性。利用箱型圖剔除異常值獲取離群數據（包含離群數據1 834條），剔除離群數據后缺失數據分布如圖5所示。

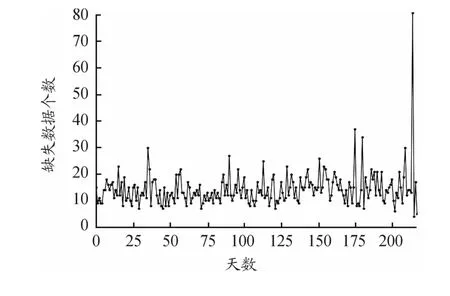
圖5 剔除異常值后的缺失數據分布

圖4、5橫坐標表示第n個工作日，縱坐標為缺失數據個數。由圖5可知，2018.07.21—2019.06.26期間，該路段每天的缺失和異常數據大多穩定在5～25，缺失比例在2%～9%，只有個別工作日的缺失值個數超過10%。

3.3 GA-RF的缺失值修復

交通流預測時間窗口為5，即利用待修復時刻的前5個時刻的交通流數據作為特征列對模型進行訓練、預測，然后利用預測結果對缺失數據進行修復。將2019年6月14日之前的工作日數據作為訓練數據集，用GA對RF的n＿estimators、max＿depth、min＿samples＿leaf以及min＿samples＿split4個參數進行聯合尋優，以MAE作為目標函數返回值，衡量在每種參數組合下模型在未知數據上的準確率，誤差越大，表明模型的預測效果越不好，因此，全局優化是一個求最小值的過程，設置初始種群中個體NIND為10，迭代次數為200，交叉概率pc為0.7，變異概率pm為0.1。

在利用遺傳算法確定最佳參數組合的200次迭代中，各參數搜索空間如表3所示。

表3 待優化參數搜索空間

經過訓練，訓練結果如圖6所示，橫坐標代表迭代次數，縱坐標代表MAE，在GA-RF模型中，隨迭代次數的增加，模型在驗證集上最優解的MAE越來越小，最終呈現為平行于x軸的一條直線（如圖7所示），找到搜索空間的最優解，得到最佳參數。

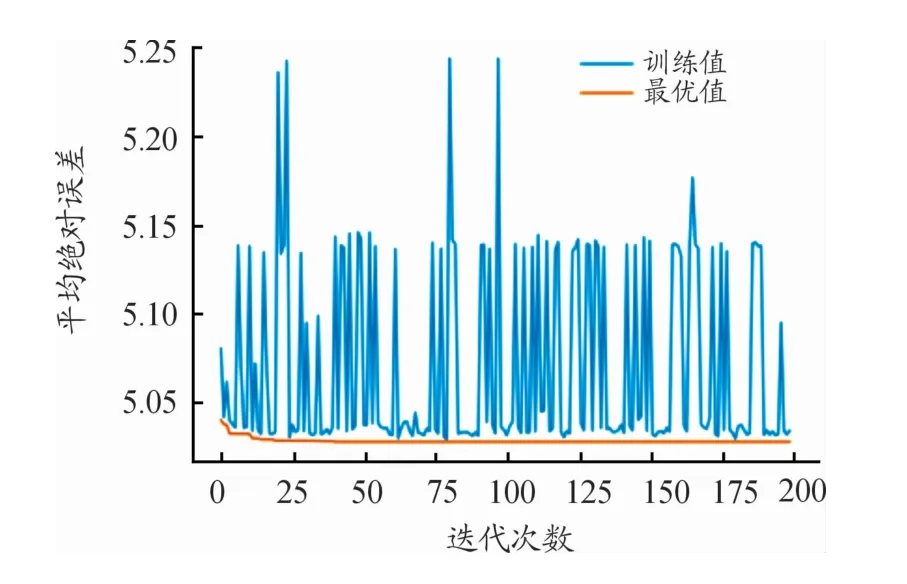
圖6 GA-RF模型訓練曲線

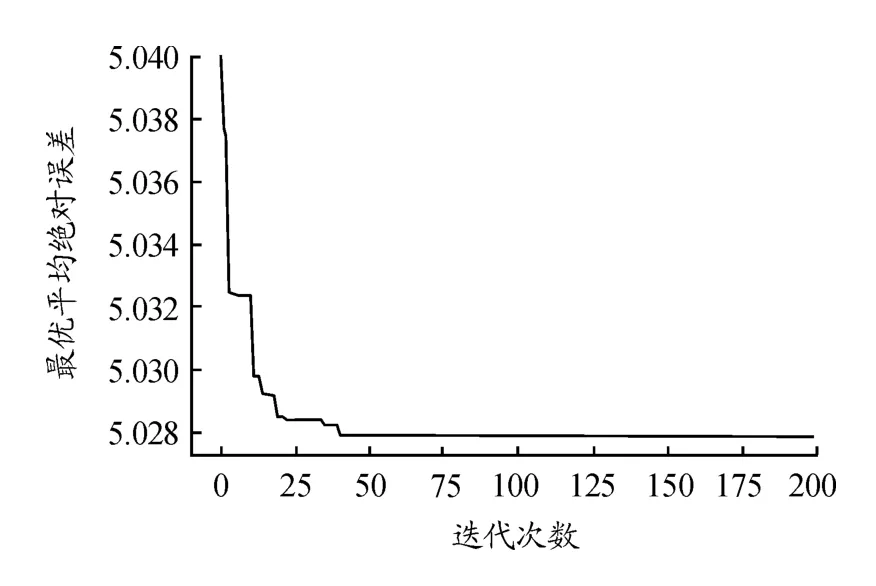
圖7 GA-RF預測模型收斂曲線

為評價模型的修復精度，在測試數據集中，選6月24日交通流數據作為測試數據，構造3%、6%缺失比例的隨機缺失數據，利用GA-RF模型分別對2種比例缺失的數據進行預測修復實驗，并將GA-RF模型預測修復結果與RF預測修復、歷史均值修復、歷史相鄰加權法結果進行對比。圖8、圖9給出了3%和6%的缺失比例下，采用RF、GA-RF、歷史均值法以及歷史相鄰加權法4種修復方法的修復結果與真實值的對比曲線，每一個marker為一缺失數據。由圖8、9可看出，GA-RF模型的預測修復結果曲線較其他幾種方式更貼近原始數據曲線。

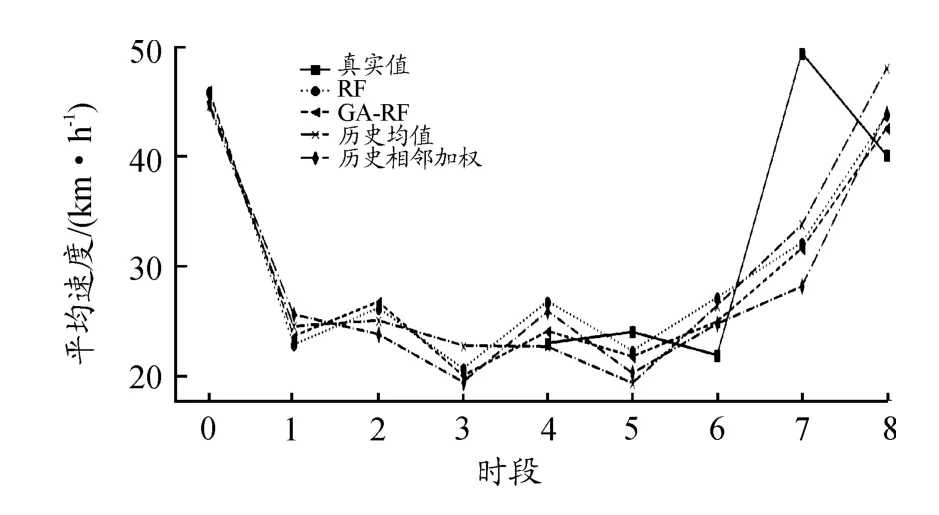
圖8 3%缺失比例下多種修復方法效果

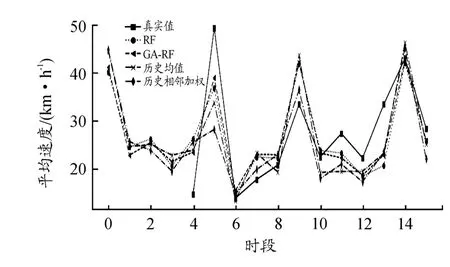
圖9 6%缺失比例下多種修復方法效果

為進一步客觀評價不同修復方法的修復效果，以MAE為主要評價指標，均方根誤差（RMSE）、均方誤差（MSE）、平均絕對百分比誤差（MAPE）評價指標作為輔助對缺失數據修復的有效性進行評價，以主要評價指標最小為目標，得到不同修復方法下的修復誤差，如表4所示。

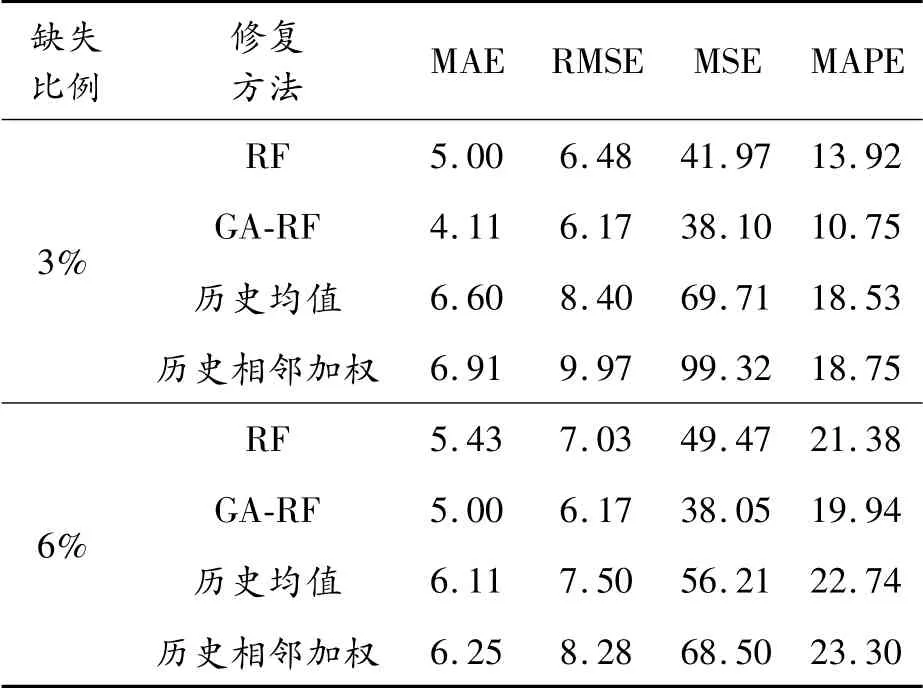
表4 不同修復方法誤差 %

從表4中可以看出，目標路段測試數據在實證的2種缺失比例下使用GA-RF模型進行預測修復的MAE、RMSE、MSE、MAPE均比RF模型、歷史均值和歷史相鄰加權的小，MAE反映了修復數據偏離真實值的程度，其值越小表示修復值與真實值的偏離程度越小，說明兩者越近，修復精度更高。

經過GA優化后的RF在2種缺失比例下的預測修復精度均得到了提升，其中，在缺失比例為3%時，參數調優后的MAE從5.00減少到4.11，準確率提升了17.8%。

3.4 路段真實缺失數據修復

利用GA-RF交通流缺失數據修復方法，將目標路段數據以天為單位進行分組循環預測修復，選取2019年6月24日的全天交通流數據，當日數據缺失比例、缺失時間分布如表5所示。

表5 真實值修復數據基礎信息

目標路段當天路段缺失值共有4個，缺失比例約1%。圖10繪制了2019年6月24日全天各時段的平均速度數據，其中“?”標識處表明該時段數據缺失，圖中為GA-RF模型預測的修復值，其余線條部分為真實交通流數據值。

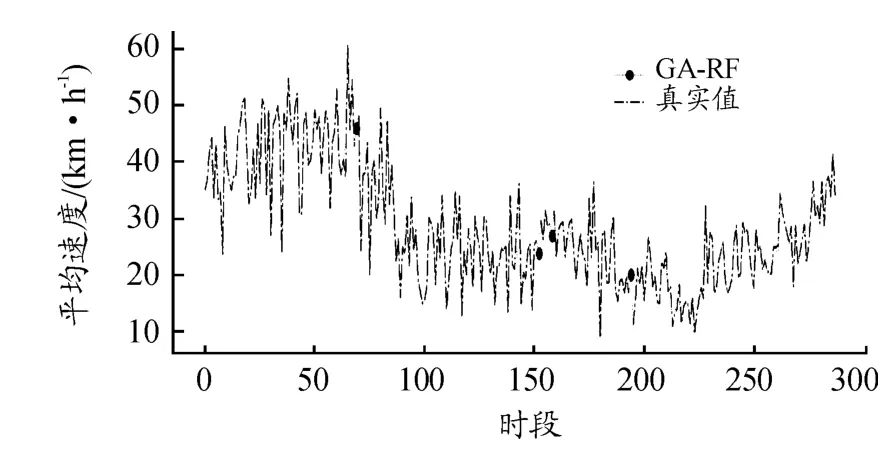
圖10 2019年6月24日缺失數據修復效果

由圖10可知，利用GA-RF模型進行預測修復的交通流缺失數據均符合路段交通流整體走勢，修復結果可靠，可作為交通流預測研究依據。

4 結論

1）基于遺傳算法優化隨機森林構建的預測模型能很好地實現對5%左右數據缺失的交通流數據修復。

2）GA-RF模型預測修復效果優于RF模型，采用GA-RF的重要參數進行尋優是有必要的，能在一定程度上降低模型的預測誤差，提升模型預測準確性。

3）采用GA-RF模型對5%左右數據缺失下的交通流進行預測修復所得到的MAE、RMSE、MSE、MAPE均低于同等缺失比例下的歷史均值法修復誤差、歷史相鄰加權法修復誤差，GA-RF模型的修復精度更高。