不同應變模型在瀝青混凝土中的適用性研究
劉珊珊
(齊齊哈爾市江東灌澇區服務中心,黑龍江 齊齊哈爾 161001)
1 緒 論
瀝青混凝土具有非常好的抗滲性能,作為柔性材質,水工瀝青混凝土適應變形的能力很強,目前我國水利工程中瀝青混凝土作為防滲體應用廣泛。瀝青混凝土面板防滲斷面形式分為簡式和復式,復式斷面結構分為封閉層、上防滲層、排水層、下防滲層、整平膠結層共5層結構,簡式斷面則省略排水層和下防滲層[1]。封閉層的作用是防止上防滲層因空氣、水等外界環境的老化作用,一般采用瀝青瑪蹄脂;上防滲層采用密級配瀝青混凝土,作用是阻止入庫滲水,整平膠結層是冬雨季節保護碎石墊層,同時作為防滲面板基礎層,優化調整下防滲層厚度,確保大壩防滲面板的材料完整性和構造連續性;整平膠結層一般采用粗級配瀝青混凝土。
2 彈性模型對應力應變的分析
2.1 完全理想彈塑性模型
塑性力學可將應力應變關系進行曲線簡化如下:
應力應變關系符合以下公式:
(1)

圖1 理想彈塑性簡化模型
2.2 用完全理想彈塑性分析瀝青混凝土拉伸
為使試件性能接近瀝青混凝土面板的現場實際碾壓性能,采用板式成型方法[2],將160℃±5℃的熱混合料裝入模具中,模型尺寸250×125×50mm,混合料插搗均勻鋪平后擊實,待試件冷卻至室溫后進行脫模,3個試件為1組,試驗前先測定試件孔隙率。

圖2 切割后的拉伸試件
本次直接拉伸試驗溫度為2℃,按加載速率1mm/min進行加載,也就是1%的應變率每分鐘。

表1 2℃條件下應變率1%拉伸試驗結果

圖3 2℃條件下應變率1%實際拉伸試驗應力應變曲線

表2 2℃理想彈塑性擬合拉伸試驗結果
3 線彈性模型對應力應變的分析
3.1 線彈性應力應變關系
若材料處于線彈性階段,即σ<σp,則應力應變成比例關系:
σ=Eε
(2)
若材料只受剪切力,在線彈性階段τ<τp,則剪應力與模量關系式為τ=Gγ,G為剪切彈性模量。平面應力狀態表達式為:
(3)
3.2 線彈性分析拉伸
本次直接拉伸試驗溫度為11℃和25℃,按加載速率1mm/min進行加載,屬于一維問題,拉伸應變等于試件伸長位移除以初始長度:
(4)
式中F拉伸荷載;A試件斷面面積;σt軸向拉伸應力:
(5)
式中:εt為軸向拉伸應變;s為軸向拉伸變形值;L為軸向量測標距100mm。
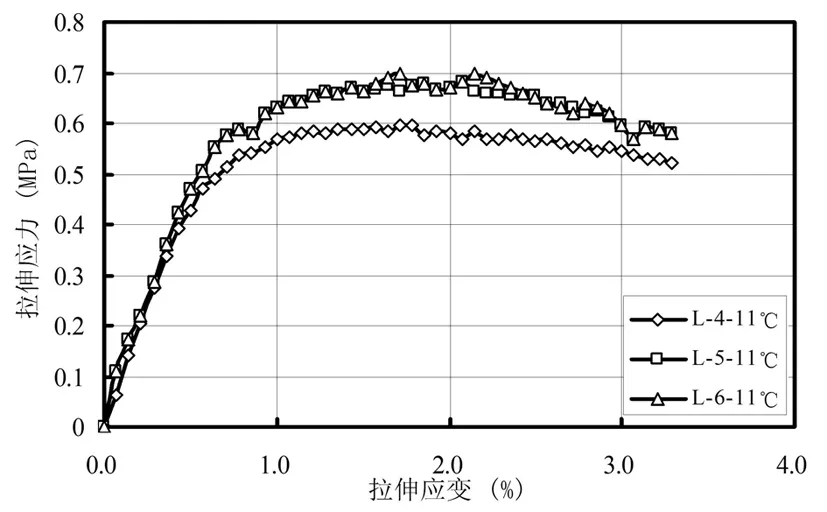
圖4 11℃條件下應變率1%的拉伸應變曲線

圖5 11℃線彈性性擬合拉伸試驗

表3 11℃線彈性性擬合拉伸試驗結果
3.4 小梁彎曲試驗計算應變的驗證

圖6 跨中受集中力小梁彎曲示意圖
對AC段分析A點的撓度為0,C點的撓度最大為
(6)
則AC段的平均撓度為
(7)
(8)
故AC段的平均撓度為C點撓度的5/8倍,近似應變AC段的平均應變應為C點的應變的5/8倍,由于軸對稱,則全梁的下表面平均應變為中點最大應變的5/8倍。在小梁彎曲試件的側面有效跨徑上打上平行線,試驗過程中用軟鋼尺測定梁下表面被拉長的距離,由于原跨徑為200mm,記錄當采集荷載達到最大值時的小梁有效跨徑下表面伸長后的長度,可得實測的下表面變形的平均應變。可判定理論計算應變的準確性和理論計算模型的可行性[3-4]。

圖7 彎曲試驗后的小梁試件
從表4中可以看出,小梁彎曲試驗時,在達到最大荷載時下表面的平均彎拉應變和理論計算的平均彎拉應變基本上是相符的,低溫2℃時小梁彎曲的應力應變關系可以用完全理想彈塑性模型來計算,在較高溫度像11℃和25℃時其小梁彎曲的應力應變關系用線彈性模型來計算是比較準確的。

表4 三種溫度下小梁下表面實測平均應變和計算平均應變
3.5 綜合分析結果
從表5可以看出同一溫度下,壓縮的強度遠大于拉伸的強度,說明瀝青混凝土是脆性材料,呈現出典型的耐壓不耐拉,故而小梁彎曲時,一部分受拉,一部分受壓,本質上是彎拉破壞。同一溫度下同一應變率下,彎拉的應變大于直接拉伸的,但小于抗壓的。當瀝青混凝土以面板的形式出現時,要著重考慮其受彎拉時的特點,在同一應變率同一溫度下,拉伸和壓縮的彈性模量基本是相同的,但在對2度的彈塑性假定下,其彈性模量大于拉伸和壓縮的,11度和25度時的彎曲彈性模量和直接拉伸與抗壓時的較為接近。從溫度方面看,當溫度增高時,瀝青混凝土強度明顯降低,應變明顯增大,彈性模量明顯降低。

表5 直接拉伸、單軸抗壓、小梁彎曲之間的比較
4 結 論
文章求解了某抽水蓄能電站瀝青混凝土面板防滲層的直接拉伸、單軸抗壓、小梁彎曲在不同溫度下的最大應變、最大應力、彈性模量,并對求解的小梁彎曲的跨中最大彎拉應變進行了驗證,分析認為2度時的小梁彎曲可用拉壓不同屈服極限彈塑性理論、11°和25°的小梁彎曲可用線彈性理論進行求解較為合理。

