FKM標準在制動夾鉗單元疲勞強度評估中的應用

孟永帥 曾梁彬 王起梁 趙金良 劉 超

(中車戚墅堰機車車輛工藝研究所有限公司 江蘇 常州 213011)

0 引言

制動夾鉗單元作為列車基礎制動裝置的執行機構，其結構的可靠性直接影響到列車運行的安全性[1]，因此在結構設計時需要對其疲勞性能進行評估。目前鐵路技術發達國家均制定了相關標準來規范疲勞強度的評估方法，如我國的《鐵道機車車輛強度設計及試驗鑒定規范》、歐洲的《鐵路應用—鐵道車輛車體結構的強度要求》、日本的《車輛用轉向架構架設計通過規則》以及國際鐵路聯盟試驗研究中心的研究報告ORE B12/RP17等[2]。

目前在進行疲勞強度評估時采用較多的是國際鐵路聯盟試驗研究中心研究報告ORE B12/RP17中的方法，該方法通過應力投影將多軸應力轉化為單軸應力，再根據構件的修正Goodman曲線進行疲勞強度評估[2]，由于該方法計算過程相對簡單，因此在鐵路行業使用范圍較廣，但該方法在評估中未考慮結構設計、制造、載荷等因素的影響。

下文采用德國機械工程研究委員會編制的FKM標準中的評估方法對制動夾鉗單元的進行疲勞強度評估，并和傳統的修正Goodman疲勞曲線強度評估結果對比分析，探索新的疲勞強度評估方法在軌道交通結構強度校核中的應用。

1 制動夾鉗單元結構

某制動夾鉗單元結構如圖1所示，主要由制動缸、球關節、吊架、杠桿、銷軸、閘片托以及閘片拖吊等零部件組成，制動夾鉗單元通過閘片拖吊螺栓和吊架橡膠球關節安裝在轉向架上。

制動時，通過向制動缸內充氣使制動缸推動杠桿向外運動，杠桿繞銷軸轉動，帶動閘片托向內運動夾緊制動盤，閘片摩擦塊和制動盤間發生摩擦耗能，從而實現列車的制動。

2 FKM標準簡介

FKM標準是德國機械工程研究委員會基于TGL標準、DIN18800、VDI2226、DIN4113-2、DIN 743、DIN EN 1999等標準以及FKM研究報告編制而成，主要用于評估鋼、鑄鐵和鋁材料結構的靜強度和疲勞強度。在評估過程中考慮了大多數對構件強度(靜態和動態)產生影響的因素，如表面粗糙度、工作溫度、殘余應力、結構細節、載荷情況等[3-4]。

標準采用名義應力法和局部應力法兩種方法對構件的靜強度和疲勞強度進行評估(見圖2)。兩種方法的評估過程基本相同，名義應力法主要適用于桿狀或者殼構件，局部應力法適用于各種構件[3]。

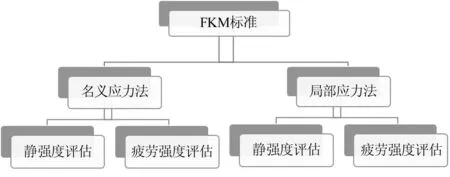
圖2 FKM標準強度評估方法

文中制動夾鉗單元的應力通過有限元模擬仿真獲得，因此選擇標準中的局部應力法進行疲勞強度評估，其評估過程如圖3所示。

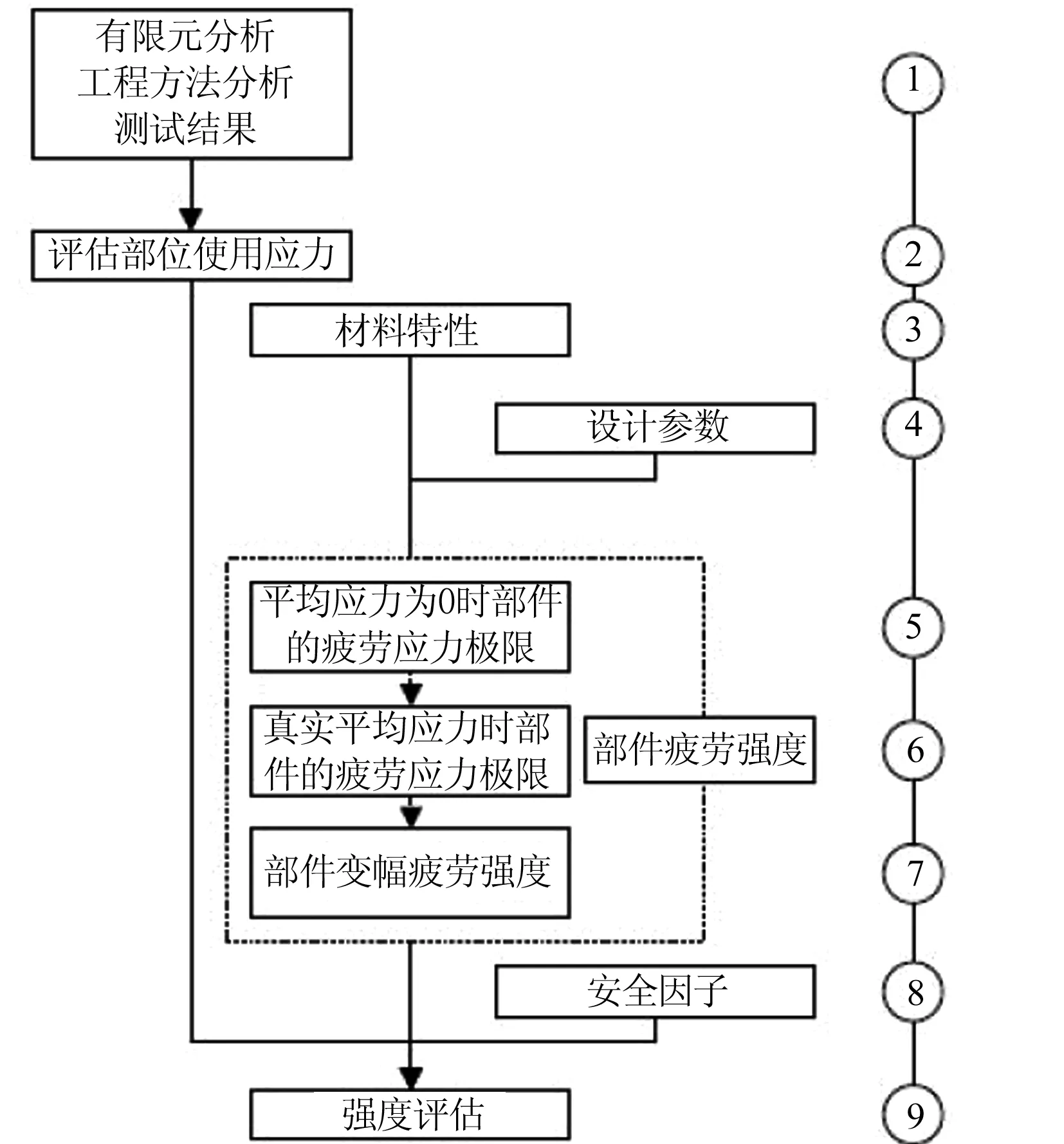
圖3 局部應力法疲勞強度評估

3 制動夾鉗單元仿真模型校核

在有限元軟件中建立仿真模型，為保證計算結果準確性，根據ASME V&V標準對仿真模型進行校核、確認[5]。首先校核仿真模型的穩定性，采用不同尺寸網格進行計算，對模型中某些節點(見圖4)的應力運用J.R.Beisheim提出的方法進行校核[6]，校核結果表明3種網格尺寸的計算結果相差很小，如表1所示，模型具有較好的穩定性。

圖4 模型校核點位置圖

表1 仿真模型校核結果

為驗證仿真模型的準確性，根據應力測試結果和ASME V&V標準，對仿真模型進行確認，結果表明，節點1和節點2的值分別為6.3%和7.6%，滿足標準要求(不大于10%)[5]，因此判定仿真模型具有較好的準確性，可以用于疲勞強度的評估分析。

圖5 制動夾鉗單元靜強度測試

有限元仿真模型校核確認后，采用1.8 mm網格模型對制動夾鉗單元的疲勞工況進行仿真計算。

4 吊架結構的疲勞強度評估

4.1 基于FKM標準的疲勞評估

取吊架的最大應力點作為危險評估點，評估點的應力值如表2所示。

表2 評估點應力值 /MPa

吊架材料為QT600，對應FKM標準中的EN-GJS-600[3]，根據標準及設計參數，計算得到材料的抗拉強度Rm為600 MPa，疲勞極限σw為204 MPa。

由于夾鉗單元在常溫環境下工作，因此在評估中不考慮高溫影響。

FKM標準通過設計系數KWK,σ來考慮疲勞缺口系數、粗糙度系數等因素對疲勞強度的影響。

(1)

按公式(1)對評估點各應力設計系數進行計算，計算過程及結果如表3所示。

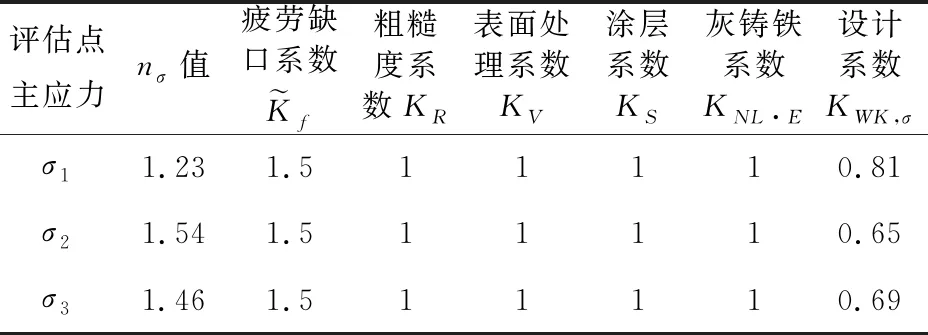
表3 評估點各應力設計系數

為考慮載荷類型對構件疲勞強度的影響，標準利用設計系數KWK，σ、平均應力系數KAK、變幅疲勞系數KBK等計算疲勞強度幅值σBK，同時考慮各應力分量疲勞強度的限值[3]。

(2)

利用公式(2)得到吊架評估點各主應力的疲勞強度幅值σBK(見表4)。

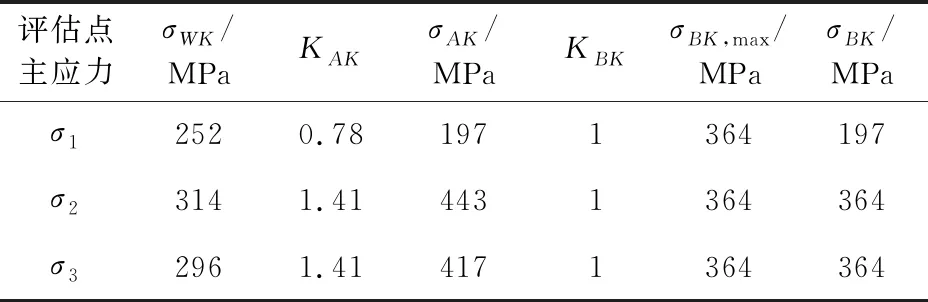
表4 各主應力疲勞強度幅值

根據制動夾鉗單元的使用情況，確定吊架的安全系數jD為1.35[3]。

FKM標準通過利用度來評估疲勞強度，當利用度小于等于1時，構件滿足疲勞強度要求。利用度分為單獨應力利用度αBK,σ和組合應力利用度αBK,σv，其計算公式為：

(3)

根據吊架的疲勞應力幅值、疲勞強度及安全系數，按公式(3)進行疲勞強度評估，其組合應力利用度為0.542，表明吊架滿足疲勞強度要求。

則基于FKM標準的疲勞強度因子[7]為：

SFKM=1/σBK，v=1/0.542=1.85

4.2 基于修正Goodman曲線的疲勞評估

根據ORE B12/RP17報告中給出的修正Goodman曲線疲勞評估方法，首先對評估點各主應力進行應力投影，將多軸狀態應力轉化為單軸狀態應力。

通過投影得到評估點的最大、最小主應力為：σmax=163.7 MPa，σmin=0。

(4)

按公式(4)得到評估點的平均應力和應力幅值分別為81.9 MPa、81.9 MPa。

吊架的材料性能為σb=600 MPa，σs=370 MPa，σ-1=249 MPa[8-9]。

根據評估點的平均應力和應力幅值，應用Smith圖形式的修正Goodman曲線進行疲勞強度評估，評估結果如圖6所示，從圖中可以看出，評估點在曲線范圍內，滿足疲勞強度要求。

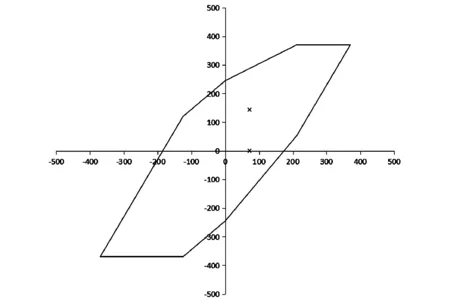
圖6 Goodman曲線評估結果

則基于修正Goodman曲線的疲勞強度因子[10]如下：

4.3 兩種評估結果對比分析

從FKM標準和Goodman方法的評估結果可以看出，兩種方法的評估結果基本一致，都可判定吊架滿足疲勞強度要求，說明FKM標準方法能夠用于疲勞強度的評估。同時FKM標準的疲勞強度因子(1.85)小于Goodman方法的疲勞強度因子(2.15)，說明FKM標準評估相對保守，結果更加可靠，且評估過程中考慮了結構設計、載荷類型等多種疲勞影響因素，因此較為科學可靠。

5 結論

本文首先利用ASME V&V標準對某制動夾鉗單元的有限元仿真模型進行校核、確認，保證了仿真模型的可靠性。在此基礎上，采用FKM標準中的局部應力法對制動夾鉗單元吊架進行疲勞強度評估，其危險點的組合利用度為0.542，滿足疲勞強度設計要求。同時和基于修正Goodman曲線的疲勞評估結果進行了對比，結果表明：FKM標準的評估結果較為安全可靠，且評估過程中考慮了較多的疲勞影響因素，過程較為科學合理，在軌道交通結構的強度評估中具有較高的應用價值。