重載鐵路牽引網雷擊仿真模型比較研究

龍 林，黃 翰，何 月

0 引言

鐵路運輸是當代大容量重載貨運較為經濟實用的運輸方式，保證鐵路的安全穩定、可靠經濟運行具有重要意義。而受雷電天氣影響，雷電導致牽引變電所頻繁跳閘、絕緣子大片破壞進而導致重載鐵路故障，威脅貨運鐵路的正常安全運行。重載鐵路供電系統中遭受雷擊的部分主要為牽引網，牽引網對于重載鐵路的可靠運行起著至關重要的作用，搭建重載鐵路牽引網仿真模型對重載鐵路系統雷擊故障研究具有重要意義[1，2]。

圍繞牽引網仿真模型搭建，目前已有相關學者做了大量的工作。文獻[3]利用PSCAD/EMTDC豐富的模型庫對帶回流線的直接供電方式和高速鐵路AT供電方式進行仿真。文獻[4，5]對眾多牽引網的仿真模型進行了總結與分析，提出仿真分析的主流傾向于通過數學模型編程實現。文獻[6]利用Matlab/Simulink建立了高速鐵路AT牽引供電系統的仿真模型，但模型不夠完善，不能完整地展現AT牽引網的所有特性。文獻[7]利用貝杰倫模型，通過在PSCAD軟件中手動輸入導線參數模塊，以高速鐵路AT供電方式下牽引網的幾何結構作為研究對象進行建模。

上述所有建模方式均是考慮高速鐵路AT供電方式下搭建牽引供電系統雷擊仿真模型。而雷擊對于重載鐵路正常運行同樣具有威脅和破壞性，上述建模未考慮搭建重載貨運鐵路牽引供電系統雷擊仿真模型。本文利用PSCAD/EMTDC仿真軟件中的互耦合線路（Mutually Coulped Wires）模型與貝杰倫（Bergeron）模型對重載鐵路中運用較為廣泛的帶回流線的直接供電方式進行仿真，針對重載鐵路牽引網搭建兩種雷擊仿真模型，通過比較仿真結果與理論數值，得出運用貝杰倫模型仿真重載鐵路牽引網雷擊故障更加準確。

1 重載鐵路牽引網

重載鐵路供電系統主要采用帶回流線的直接供電方式，其供電系統主要由牽引變電所和牽引網組成，牽引變壓器采用V-v接線方式。對于牽引網，主要由接觸線、鋼軌、回流線等構成牽引供電回路，將其稱為懸掛系統（如圖1所示），通過懸掛系統完成對電力機車的送電[8]。故在對牽引網進行仿真建模時，在不影響牽引網各導體的原始參數情況下，對懸掛系統進行合理等效和化簡至關重要。

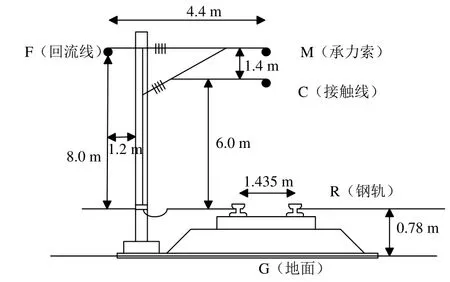
圖1 牽引網懸掛系統

2 雷電流模型

由于在眾多雷電流模型中，雙指數函數模型和實測的雷電流波形最為接近，故本文采用雙指數函數模型對雷電流波形進行仿真。雙指數函數模型數學表達式為

式中：I為雷電流幅值，kA；α、β為時間常數，s。

在PSCAD/EMTDC元件庫中選用對應的元件搭建雷電流模型，如圖2所示。模型選用雙指數函數波形模擬受控電流源波形，仿真模型中電流幅值為50 kA，波頭時間為2.6 μs，波尾時間為50 μs，

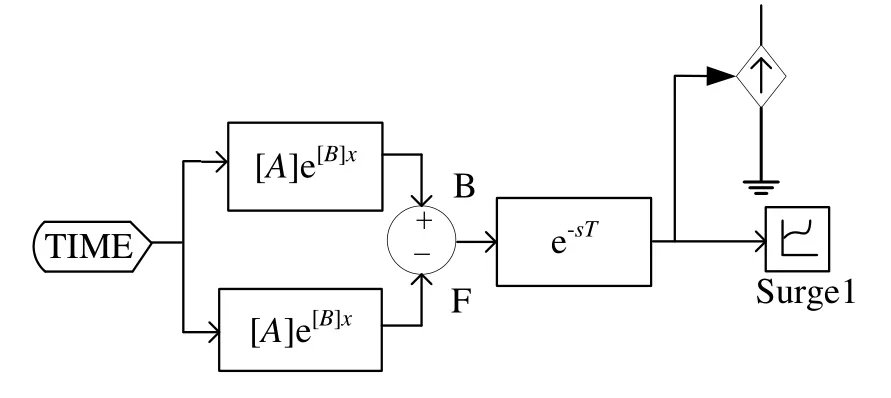
圖2 雷電流模型

在PSCAD/EMTDC中仿真標準雷電流波形如圖3所示。

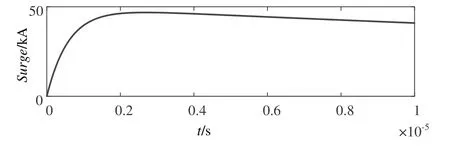
圖3 標準雷電流波形

3 仿真結果比較

本文首先利用PSCAD/EMTDC對帶回流線的直接供電方式的牽引供電系統正常和雷擊故障兩種情況進行仿真，系統仿真時間設置為2 s。牽引網長度L= 21 km，且每7 km長度的牽引網封裝為一個模塊，電力機車等效為交流電流源。

3.1 正常無雷擊仿真結果比較

在正常無雷擊情況下，分別采用互耦合模型和貝杰倫模型進行仿真，整體仿真模型如圖4所示。通過仿真可得變壓器出口處即接觸線首端電壓Ecup波形如圖5所示。

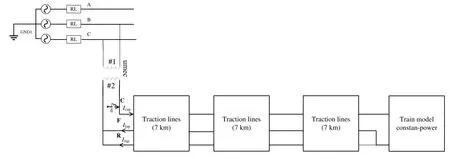
圖4 正常無雷擊系統仿真模型

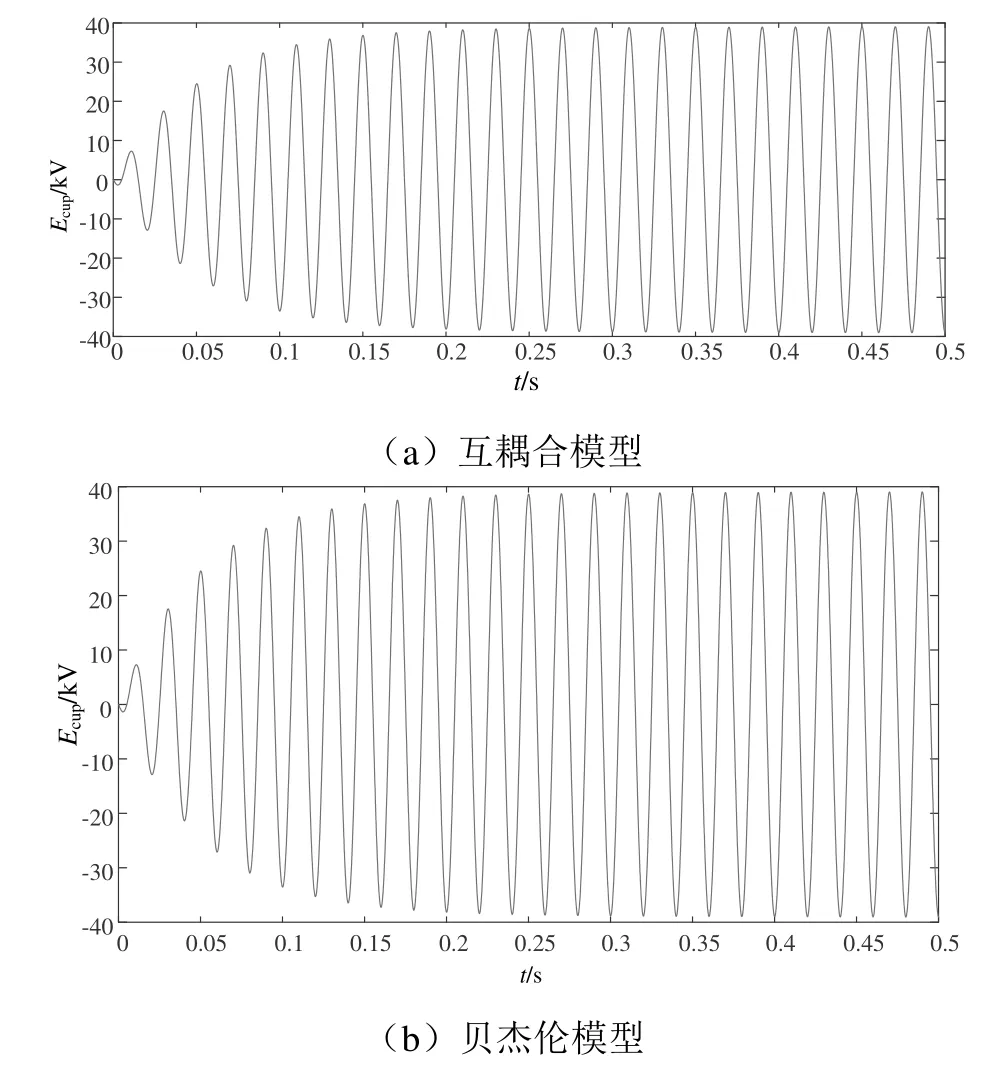
圖5 接觸線首端電壓Ecup波形

根據上述仿真結果可知，互耦合模型接觸線首端電壓Ecup穩定值為39.35 kV，貝杰倫模型接觸線首端電壓Ecup穩定值為39.31 kV，接觸線首端電壓理論值為二者基本相符。

通過上述正常無雷擊的兩種模型仿真，可得變壓器出口處即接觸線首端電流Icup、回流線首端電流Ifup、鋼軌首端電流Irup、承力索首端電流Imup仿真波形分別如圖6～圖9所示。

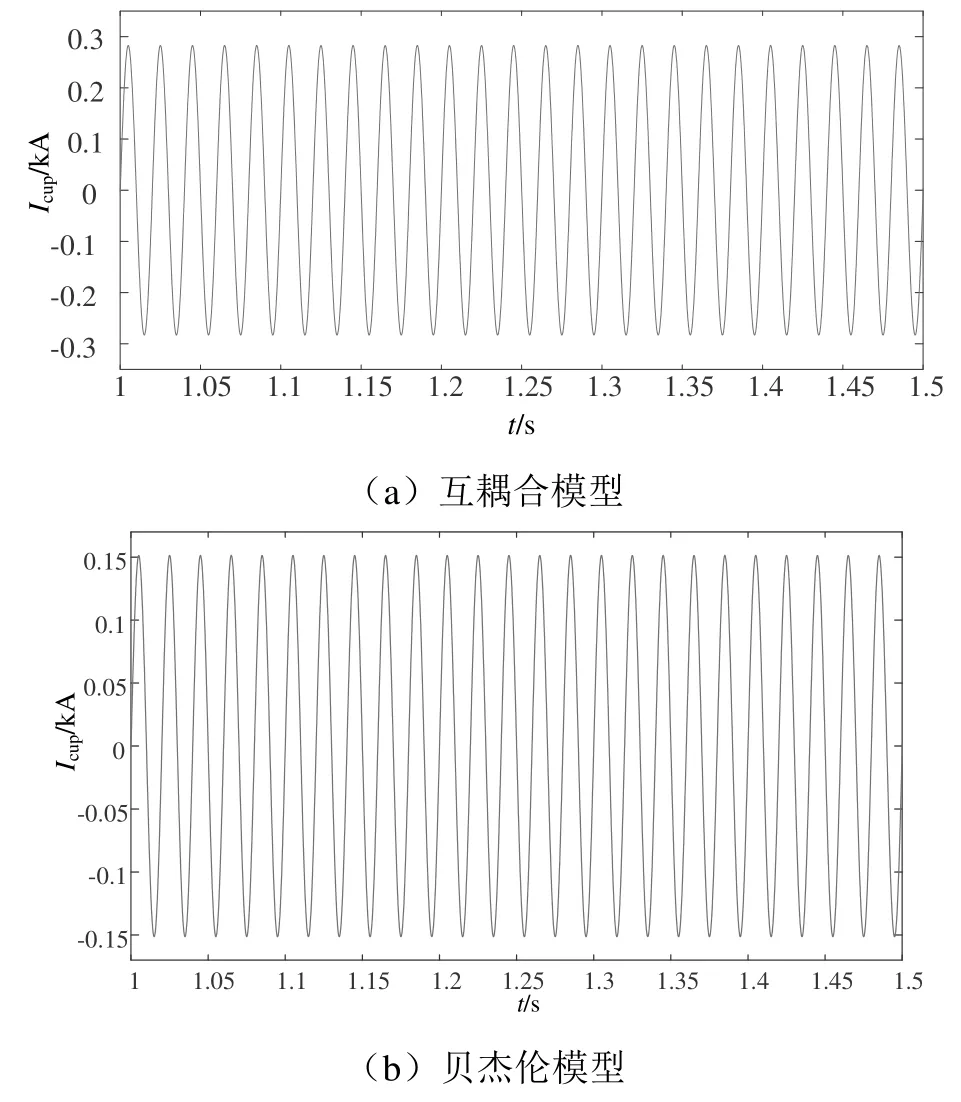
圖6 接觸線首端電流Icup波形

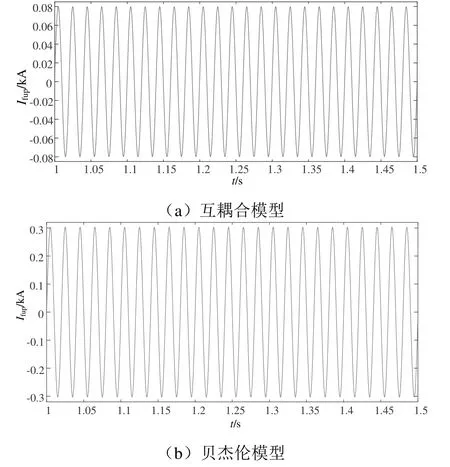
圖7 回流線首端電流Ifup波形

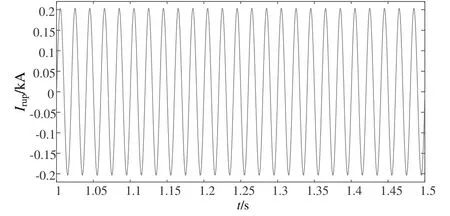
圖8 鋼軌首端電流Irup波形

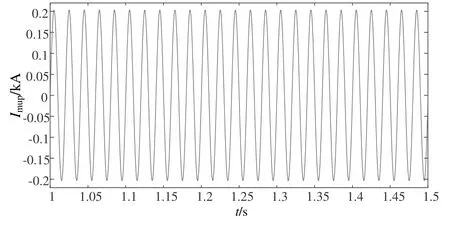
圖9 承力索首端電流Imup波形

由上述仿真波形結果可知，受整個系統電容參數的影響，接觸線首端電流Icup、回流線首端電流Ifup、鋼軌首端電流Irup、承力索首端電流Imup均在仿真開始1 s后趨于穩定并不再呈現波動的趨勢。互耦合模型接觸線首端電流Icup、回流線首端電流Ifup、鋼軌首端電流Irup穩定值分別為0.28、0.08、0.20 kA。貝杰倫模型接觸線首端電流Icup、回流線首端電流Ifup、承力索首端電流Imup穩定值分別為0.151、0.301、0.2 kA。互耦合模型中鋼軌首端電流Irup和回流線首端電流Ifup方向均與接觸線首端電流Icup方向相反，并且Irup與Ifup之和等于Icup。貝杰倫模型中接觸線與承力索共同傳遞電流，接觸線首端電流Icup和承力索首端電流Imup方向相同，且二者電流方向均與回流線首端電流Ifup方向相反。仿真結果符合帶回流線直接供電方式的重載鐵路供電系統的電流分布，綜合兩種模型接觸線首端電壓和電流的仿真結果可見所建立仿真模型基本正確。

3.2 雷擊故障仿真結果比較

在雷擊情況下，同樣采用互耦合雷擊模型和貝杰倫雷擊模型進行仿真，通過多次改變雷電流幅值與雷擊接觸線位置可得變壓器出口處即接觸線首端電壓Ecup，接觸線首端電流Icup，接觸線末端電流Icend仿真波形。

t= 1.5 s時刻，在接觸線14 km處加入幅值I=50 kA的標準雷電流，接觸線首端電壓Ecup、接觸線首端電流Icup、接觸線末端電流Icend、雷電流Surge仿真波形分別如圖10～圖13所示。

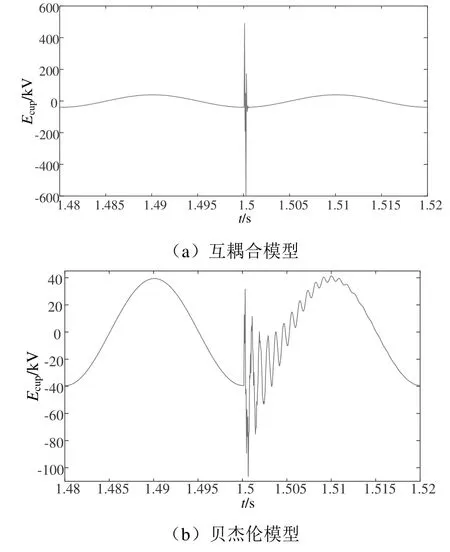
圖10 接觸線首端電壓Ecup波形

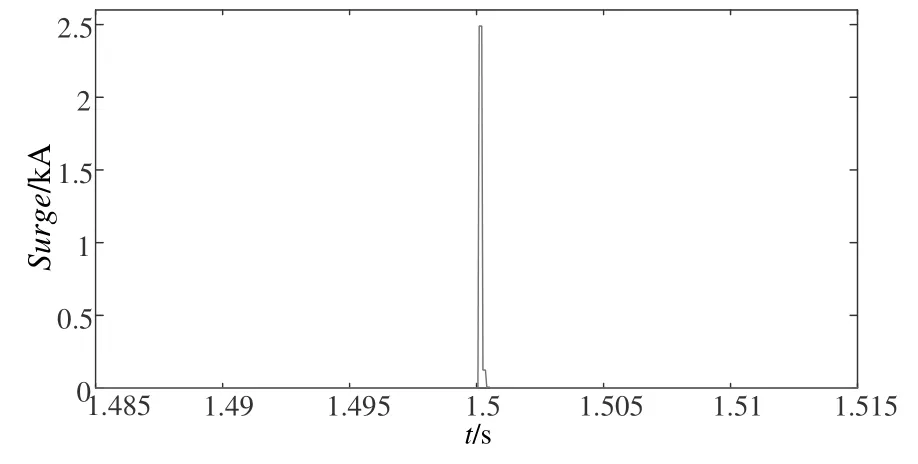
圖13 雷電流Surge仿真波形

由圖10仿真結果可知，在雷擊故障發生前后，兩種模型下的接觸線首端電壓Ecup均維持在正常無雷擊情況下的穩定值。對于互耦合模型，發生雷擊故障時，接觸線首端電壓Ecup在雷擊時出現高達429 kV的雷擊過電壓。對于貝杰倫模型，發生雷擊故障時，接觸線首端電壓Ecup發生突變，出現高達104 kV雷擊過電壓。

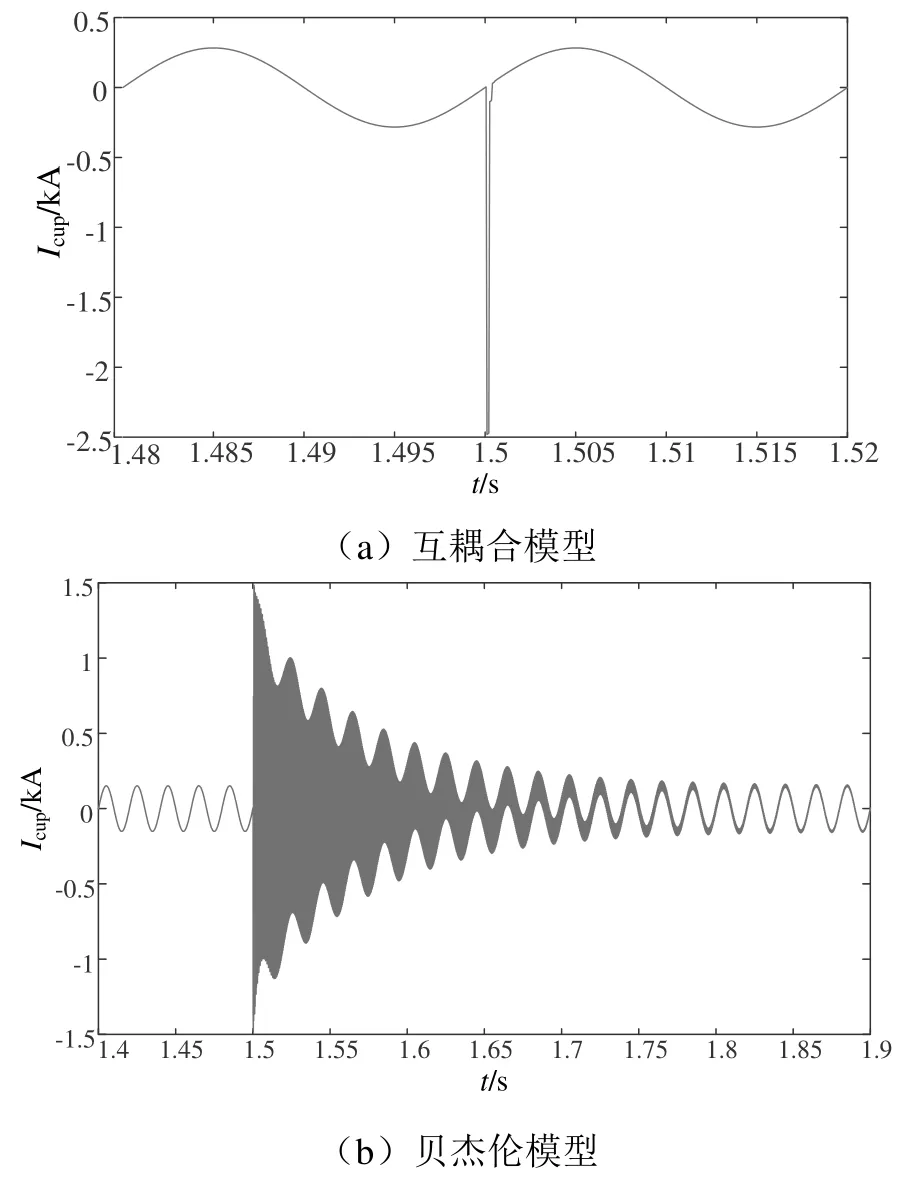
圖11 接觸線首端電流Icup波形

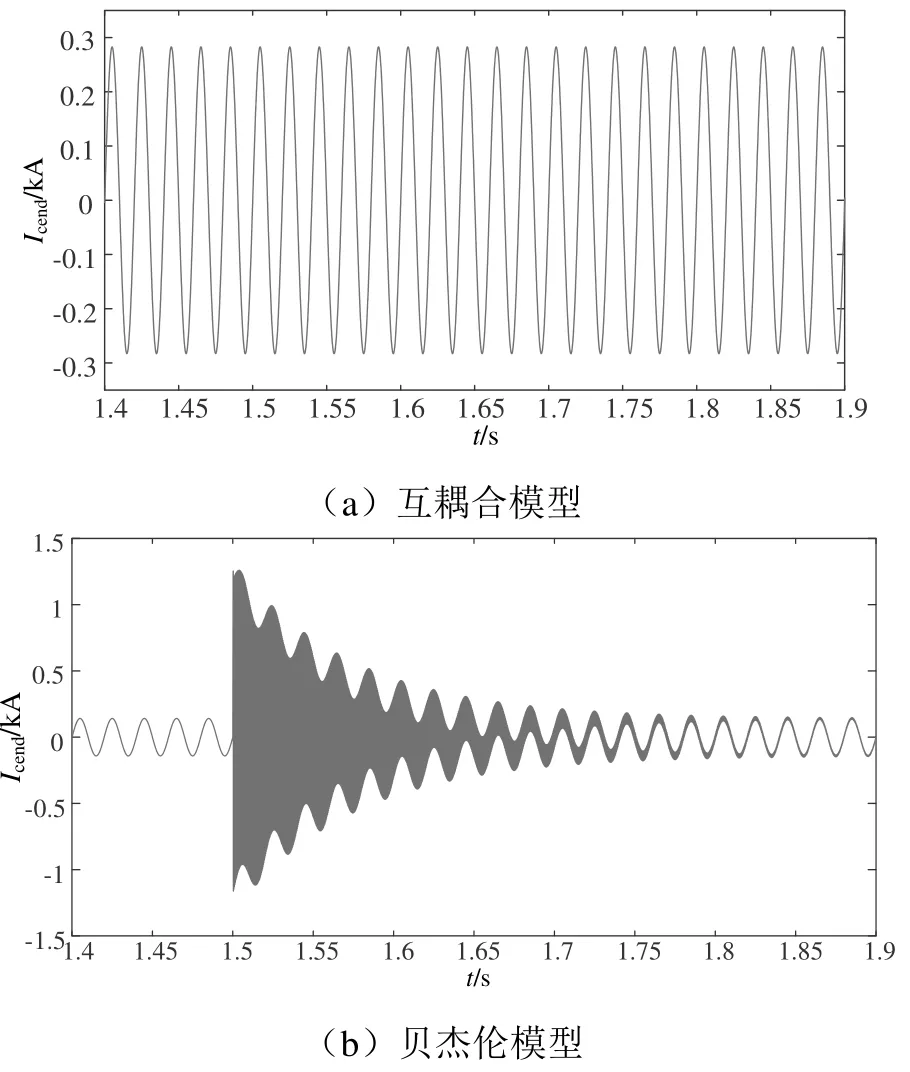
圖12 接觸線末端電流Icend波形

比較仿真結果可知，在雷擊故障前，兩種模型下的接觸線首端電流Icup與接觸線末端電流Icend均維持在正常穩定值，發生雷擊故障時，互耦合模型中接觸線首端電流Icup電流峰值突變為2.47 kA，而接觸線末端電流Icend未出現突變特征。貝杰倫模型中接觸線首端電流Icup電流峰值突變為1.45 kA，接觸線末端電流Icend突變為1.252 kA。互耦合模型Icup突變值2.47 kA相對于雷電流仿真波形峰值2.48 kA基本保持不變，說明損耗較小，而接觸線末端電流Icend并未出現突變特征。貝杰倫模型中Icup峰值1.45 kA，Icend峰值1.252 kA相對于雷電流仿真波形峰值2.48 kA具有明顯的損耗和衰減。

t= 1.5 s時刻，在接觸線7 km處加入幅值I= 50 kA的標準雷電流，接觸線首端電壓Ecup、接觸線首端電流Icup、接觸線末端電流Icend波形分別如圖14～圖16所示。

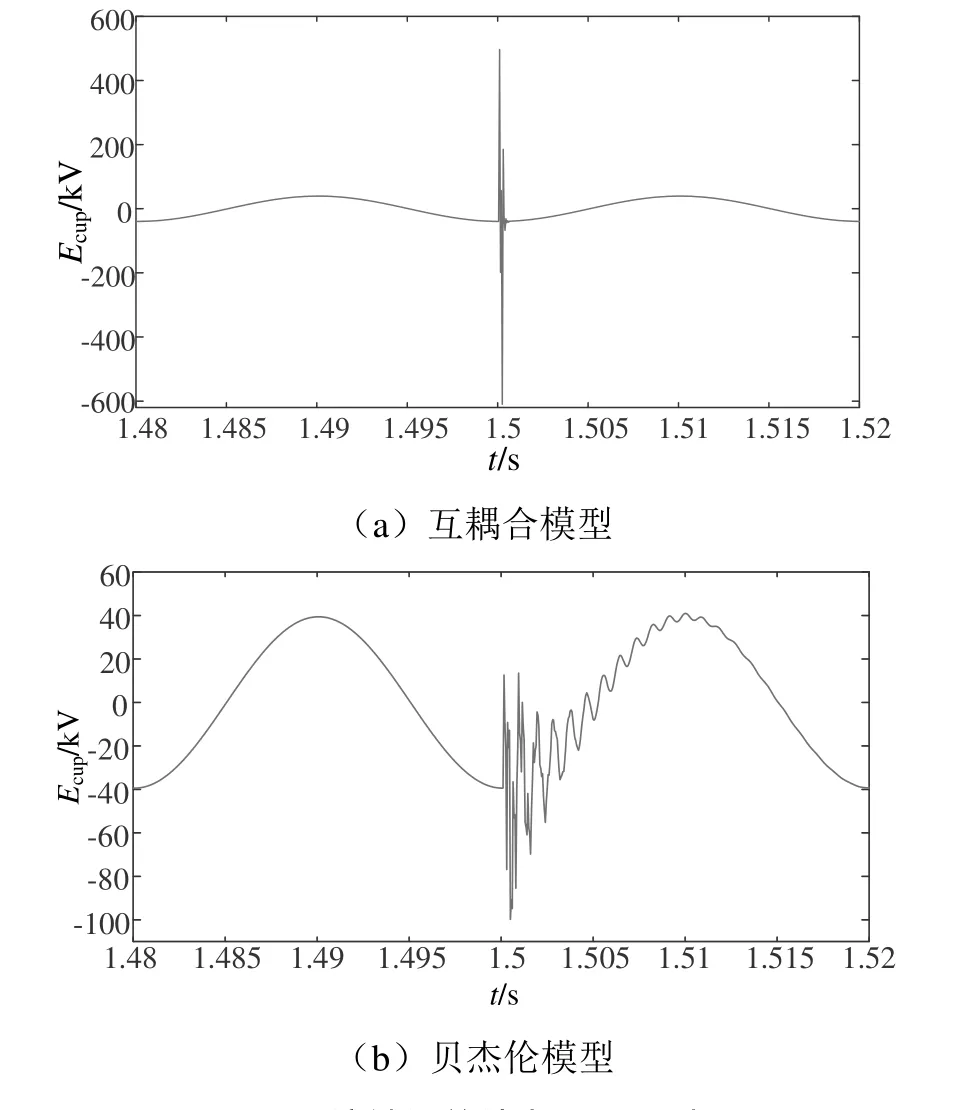
圖14 接觸線首端電壓Ecup波形

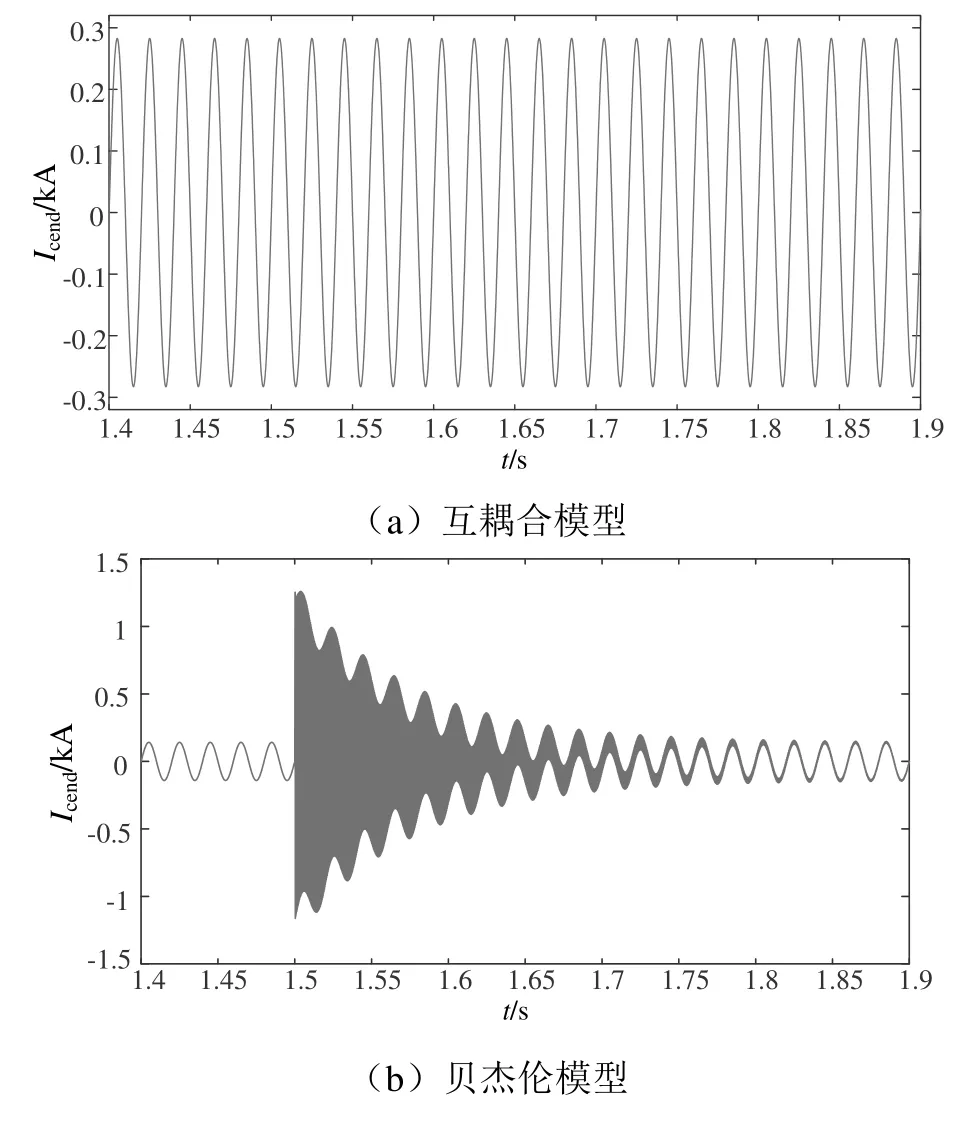
圖16 接觸線末端電流Icend波形

通過改變雷擊接觸線位置，由上述仿真結果可知，當雷擊接觸線7 km處時，在雷擊故障發生前后，與雷擊接觸線14 km處時相同，兩種模型下的接觸線首端電壓Ecup均維持在正常無雷擊情況下的穩定值。對于互耦合模型，發生雷擊故障時，接觸線首端電壓Ecup在雷擊時出現高達480.7 kV的雷擊過電壓。對于貝杰倫模型，發生雷擊故障時，接觸線首端電壓Ecup發生突變，出現高達99 kV雷擊過電壓。

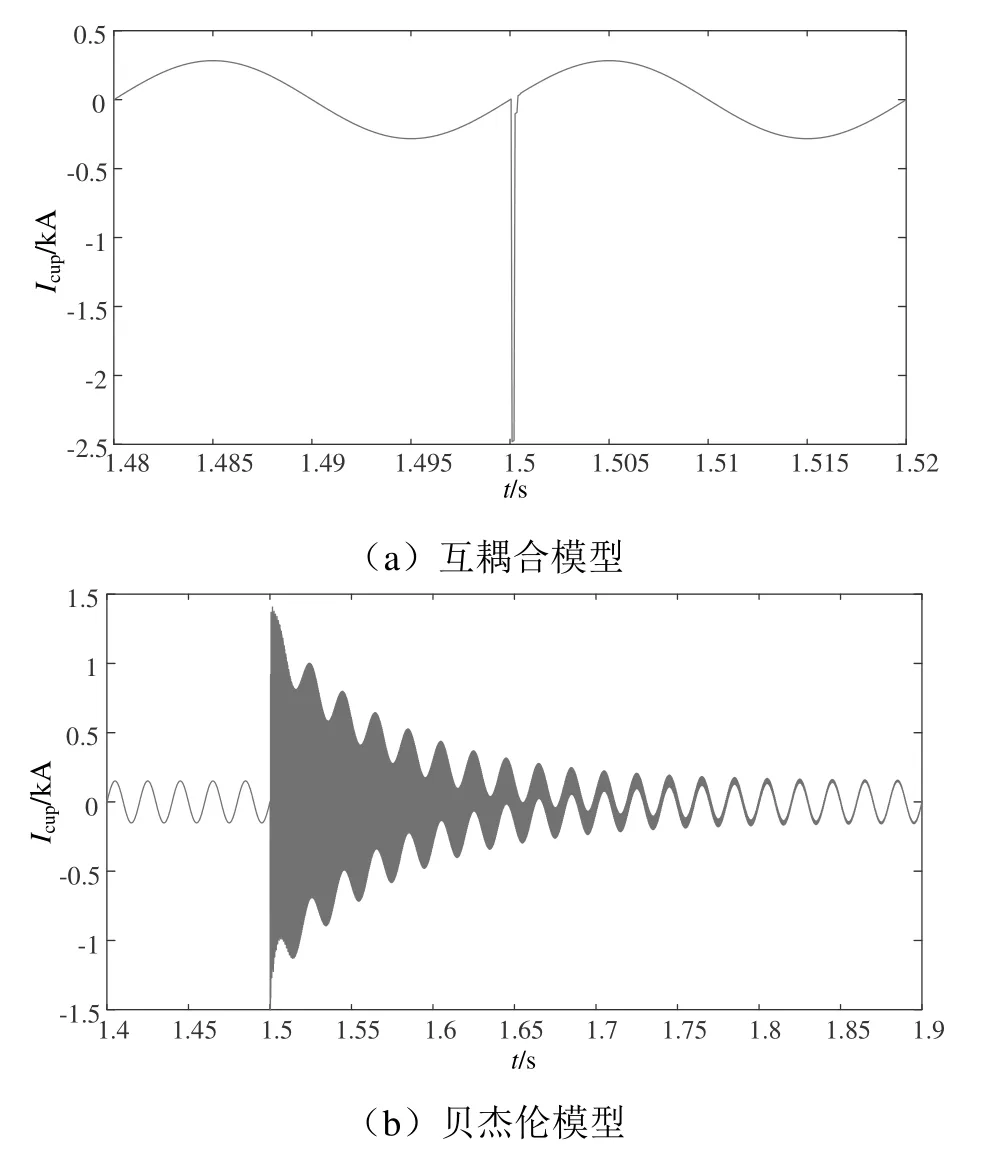
圖15 接觸線首端電流Icup波形

當雷擊接觸線7 km處，由上述仿真結果可知，兩種模型下的接觸線首端電流Icup與接觸線末端電流Icend在雷擊之前均維持在正常穩定值，發生雷擊故障時，互耦合模型中接觸線首端電流Icup峰值突變為2.476 kA，而接觸線末端電流Icend未出現突變特征。貝杰倫模型中接觸線首端電流Icup峰值突變為1.3 kA，接觸線末端電流Icend突變為1.257 kA。互耦合模型Icup突變值2.476 kA相對于雷電流仿真波形峰值2.48 kA與雷擊接觸線14 km處類似基本保持不變，說明損耗較小，而接觸線末端電流Icend同樣并未出現突變特征。而貝杰倫模型中Icup峰值1.3 kA，Icend峰值1.257 kA，相對于雷電流仿真波形峰值2.48 kA具有明顯的損耗和衰減。

t= 1.5 s時刻，在接觸線14 km處加入幅值為30 kA的雷電流，接觸線首端電壓Ecup、接觸線首端電流Icup波形、接觸線末端電流Icend、雷電流Surge仿真波形如圖17～圖20所示。

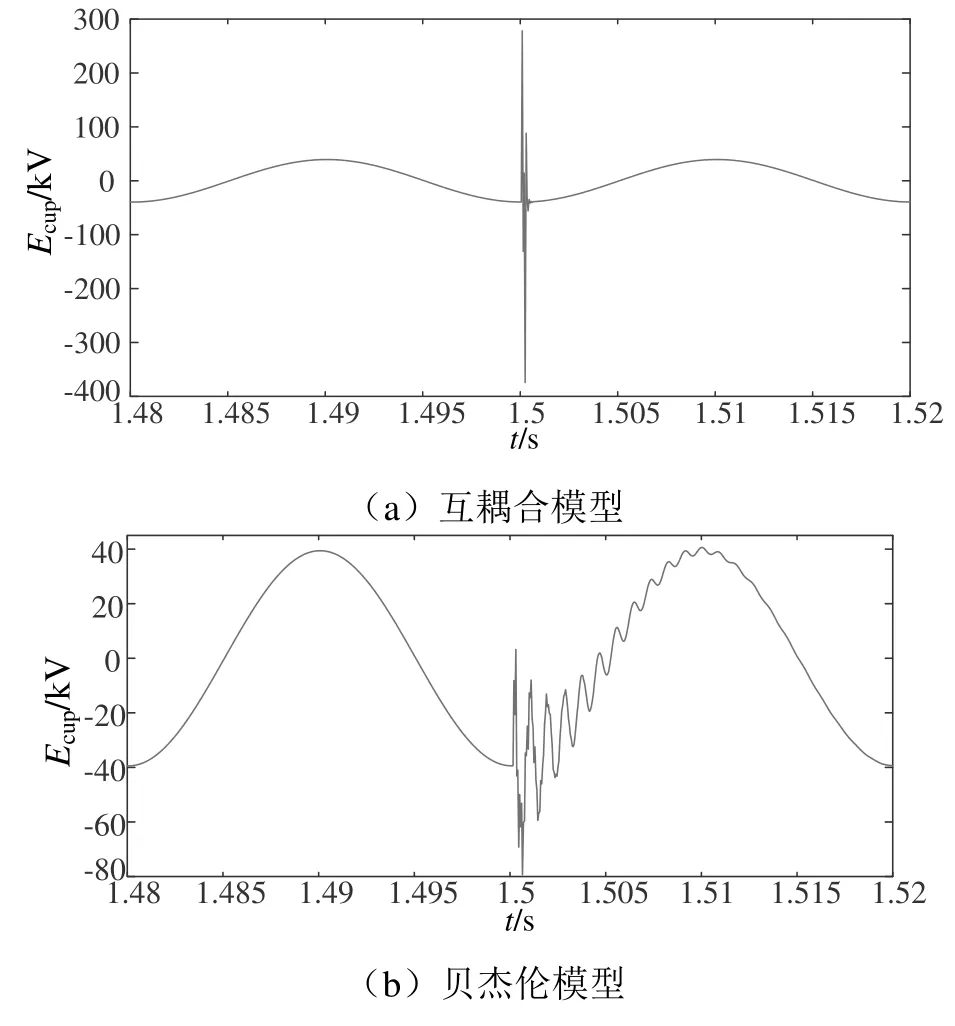
圖17 接觸線首端電壓Ecup波形

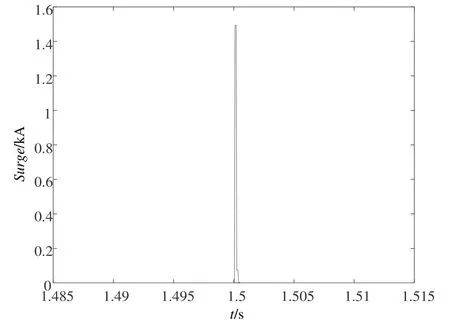
圖20 雷電流Surge仿真波形

通過改變雷電流幅值，當雷電流幅值I= 30 kA時，對于互耦合模型，發生雷擊故障時，接觸線首端電壓Ecup在雷擊時出現高達356 kV的雷擊過電壓。對于貝杰倫模型，發生雷擊故障時，接觸線首端電壓Ecup發生突變，出現高達78 kV雷擊過電壓。可見，相對于相同雷擊點雷電流幅值I= 50 kA的突變值，改變雷電流幅值后兩種模型下的雷擊過電壓均有所減小。

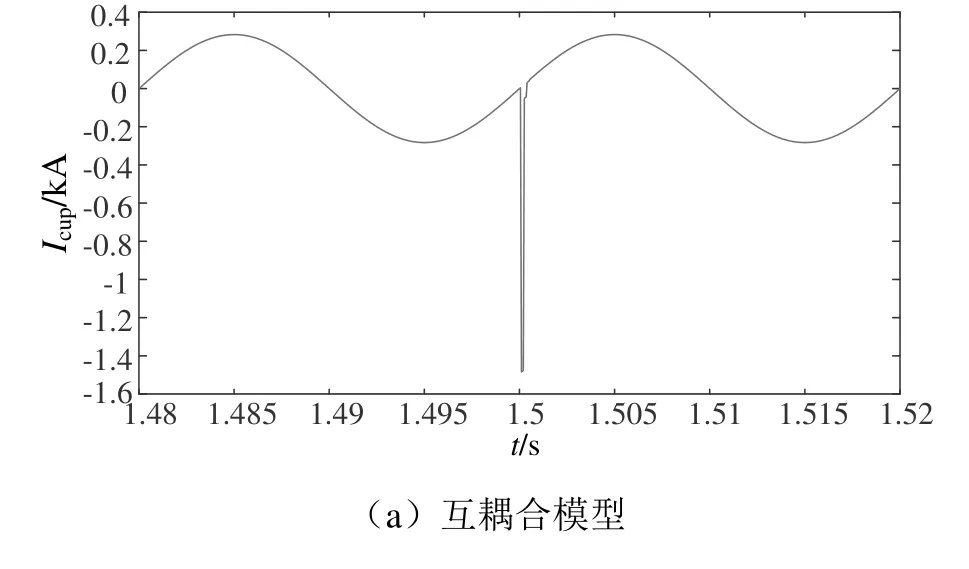
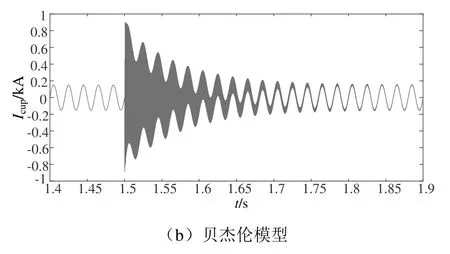
圖18 接觸線首端電流Icup波形

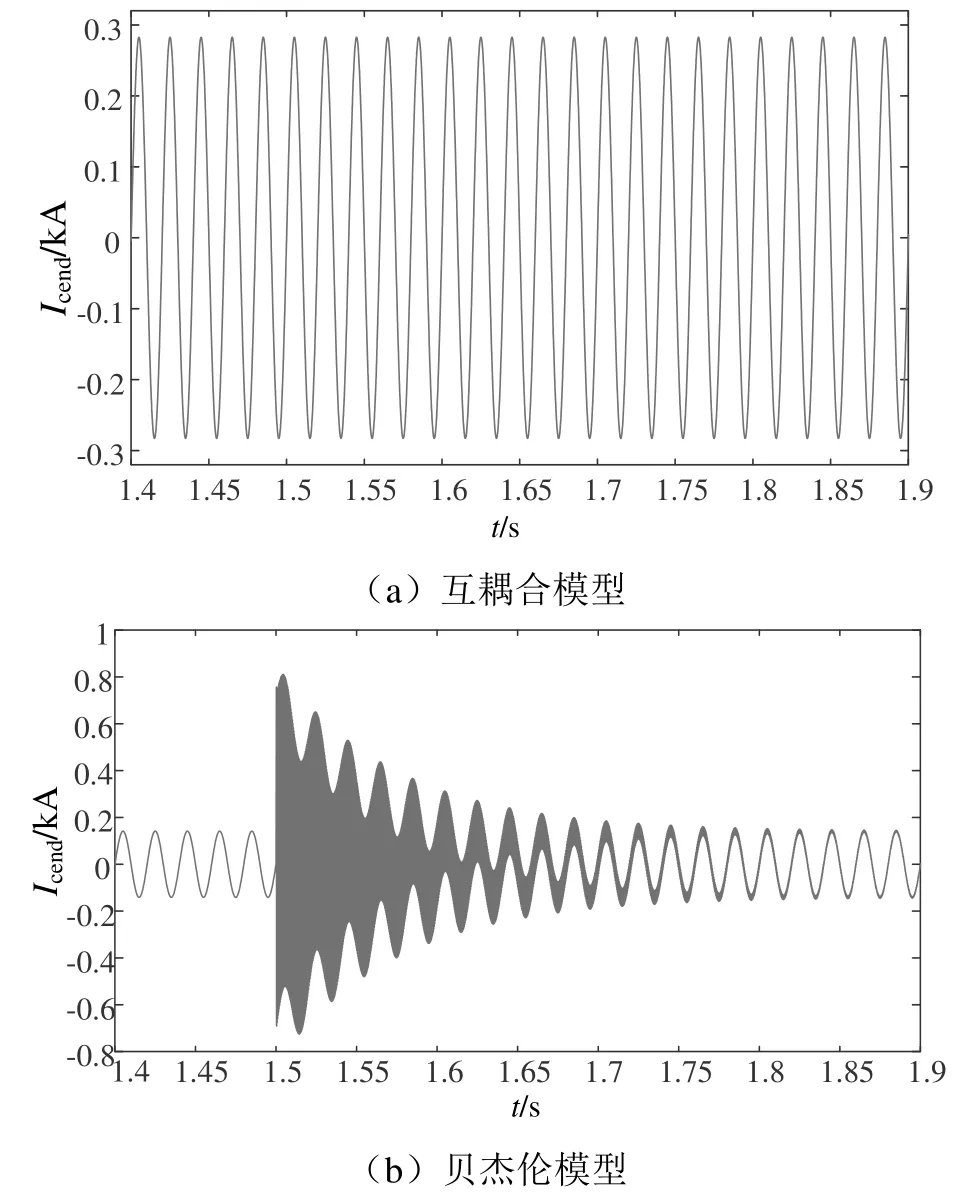
圖19 接觸線末端電流Icend波形

當雷電流幅值I= 30 kA時，由仿真波形圖可知，互耦合模型中接觸線首端電流Icup電流峰值突變為1.48 kA，相對于雷電流幅值I= 50 kA下的Icup突變值2.47 kA明顯減小，接觸線末端電流Icend同樣保持穩定，未出現突變特征。貝杰倫模型中，接觸線首端電流Icup電流峰值突變為0.84 kA，相對于雷電流幅值I= 50 kA情況下的Icup突變值1.45 kA同樣明顯衰減，接觸線末端電流Icend突變為1.257 kA具有與Icup相同的衰減特征。

綜合以上仿真結果，互耦合模型是模擬單位長度下3條相互耦合的導體模型，是以輸入導體自電阻、自電感以及導體之間的互電感的形式表征集中參數進而仿真。通過改變雷擊接觸線的不同位置、不同雷電流幅值后，仿真接觸線首端電壓Ecup和電流Icup、接觸線末端電流Icend發現，互耦合模型表征雷電流在牽引網導體內傳導時的損耗特性較弱、準確性較低，且無法表征雷電流在接觸線末端的故障特性，更無法充分準確表征導體之間的電磁互耦合關系。而在電磁暫態模型中主要包括貝杰倫模型、JMarti模型、Semlyen模型，由于牽引網跨距較短且本文主要考慮雷擊重載鐵路牽引網，故采用貝杰倫模型對其建模。貝杰倫模型采用分布式LC參數和集總電阻的行波線路模型，是以分布式方式來代表PI段的L和C元件，同樣仿真接觸線首端電壓Ecup和電流Icup、接觸線末端電流Icend發現，雷電流傳導至接觸線首端和末端時，Ecup、Icup和Icend突變值相對互耦合模型較小且損耗較大，說明在貝杰倫模型下，表征雷擊后各電氣量特性更為準確，可以更好地表征重載鐵路牽引網各導體之間的電磁耦合關系及雷電流在牽引網中的衰減特性。

4 結論

本文利用PSCAD/EMTDC搭建了重載鐵路系統正常和雷擊故障兩種狀態下的仿真模型。通過比較正常情況下互耦合模型與貝杰倫模型仿真電氣量與理論值發現，二者模型均是基本正確的。在比較雷擊故障情況下互耦合雷擊模型與貝杰倫模型發現，雖然互耦合模型能夠表征牽引網各導體之間的部分電磁互耦合關系，但相對于貝杰倫雷擊模型仿真而言，貝杰倫模型在仿真雷擊故障時能夠更好地表征重載鐵路牽引網各導體之間的電磁耦合關系及雷電流在牽引網中的衰減特性。在對重載鐵路進行牽引網雷擊故障仿真研究時，運用貝杰倫模型作為懸掛系統導線模型，對重載鐵路牽引網幾何結構進行建模具有更好的仿真效果和參考價值。