基于改進IGG3權函數(shù)距離誤差模型的工業(yè)機器人標定

張恩政 唐寧敏 陳 剛 劉翠蘋

1.浙江理工大學精密測量實驗室，杭州，3100182.杭州市質量技術監(jiān)督檢測院機器人實驗室，杭州，3100193.杭州新松機器人自動化有限公司，杭州，311225

0 引言

工業(yè)機器人具有重復性定位精度較高、穩(wěn)定可靠、能在高危環(huán)境下作業(yè)等優(yōu)勢，在傳統(tǒng)制造業(yè)、特別是勞動密集型產(chǎn)業(yè)的轉型升級中發(fā)揮著重要作用[1]。工業(yè)機器人具有的較高重復性定位精度基本可滿足空間位置點的定位精度需求，但難以滿足目前一些領域對高絕對定位精度的要求[2]。機器人長時間的使用以及磨損也會導致絕對定位精度的下降[3-4]，因此，對工業(yè)機器人進行適時標定以確保其處于較高的絕對定位工作精度是機器人應用中的重要環(huán)節(jié)。

工業(yè)機器人的標定過程大致包括建模、測量、辨識和補償四個步驟[5]，其中模型參數(shù)辨識是標定過程的關鍵步驟。為提高工業(yè)機器人運動學模型參數(shù)的準確度，國內外已開展了機器人標定方法的大量相關研究，基本可分為基于位置誤差模型的標定和基于距離誤差模型的標定。

基于位置誤差模型的標定是目前常用的方法，JIANG等[6]提出了基于卡爾曼和粒子濾波的機器人位置誤差模型運動學標定方法；房立金等[7]提出了基于量子粒子群優(yōu)化算法的幾何參數(shù)標定方法，利用優(yōu)化獲得的參數(shù)修正量更新運動學模型；溫秀蘭等[8]提出了基于改進粒子群算法的機器人幾何參數(shù)標定方法，并進一步提高了機器人的標定精度。MESSAY等[9]提出使用結合模擬退火和信任區(qū)域的新型混合算法進行參數(shù)辨識；張強等[10]針對機器人手眼標定過程中存在的測量粗差影響標定精度的問題，提出了一種誤差分布估計的機器人手眼標定算法，在一定程度上提高了機器人手眼標定精度；向民志等[11]提出基于抗差估計的工業(yè)機器人位置誤差標定算法，相較于傳統(tǒng)最小二乘法擬合算法，所提算法在進行機器人標定時的精度更高且魯棒性更強；KLIMCHIK等[12]考慮了粗差對機器人末端定位的影響，增加了一個歸一化因子，但對粗差的處理較為粗略。

上述基于位置誤差模型的標定方法存在機器人坐標系與測量設備坐標系轉換時的轉換誤差對標定精度產(chǎn)生影響的共性問題，為了解決該問題，基于距離誤差模型的標定方法被提出并已應用到機器人標定中。姚興田等[13]提出將距離誤差模型應用于服務機器人運動學標定方法中，提高了服務機器人的絕對定位精度；李定坤[14]利用基于距離誤差模型的最小二乘算法辨識運動學參數(shù)，通過最小化殘差的平方和來求取數(shù)據(jù)的最佳匹配值，但當標定采樣點中存在測量粗差值時，則會繼續(xù)將粗差值代入計算，這部分粗差值對殘差平方和的影響比其他觀測值要大得多，從而會使得估計量受到嚴重影響。由此可知，基于距離誤差模型的標定方法可避免出現(xiàn)坐標系轉換引入附加誤差的問題，但標定過程中測量數(shù)據(jù)的粗差仍然會對標定結果產(chǎn)生較大影響。

針對基于距離誤差模型的機器人標定方法中測量粗差數(shù)據(jù)會對標定精度產(chǎn)生影響的問題，本文提出了一種基于改進IGG3權函數(shù)距離誤差模型的工業(yè)機器人標定方法，將改進的IGG3權函數(shù)最小二乘辨識算法應用于工業(yè)機器人距離誤差的標定中，從消除坐標系轉換誤差和減小數(shù)據(jù)粗差影響的角度提高工業(yè)機器人的標定精度。

1 機器人距離誤差模型建立

1.1 運動學模型

本文以SR4C型工業(yè)機器人為研究對象進行Denavit-Hartenberg(D-H)運動學建模，該機器人為六自由度串聯(lián)機械臂，具體包括腰部回轉、大臂俯仰、小臂俯仰、手腕回轉、手腕俯仰、手腕側擺六個自由度。為了建立D-H模型，首先要對機器人的每一個關節(jié)建立坐標系統(tǒng)，如圖1所示，其中，機器人的基坐標系{W0}(O0x0y0z0)和第一關節(jié)坐標系{W1}(O1x1y1z1)重合。

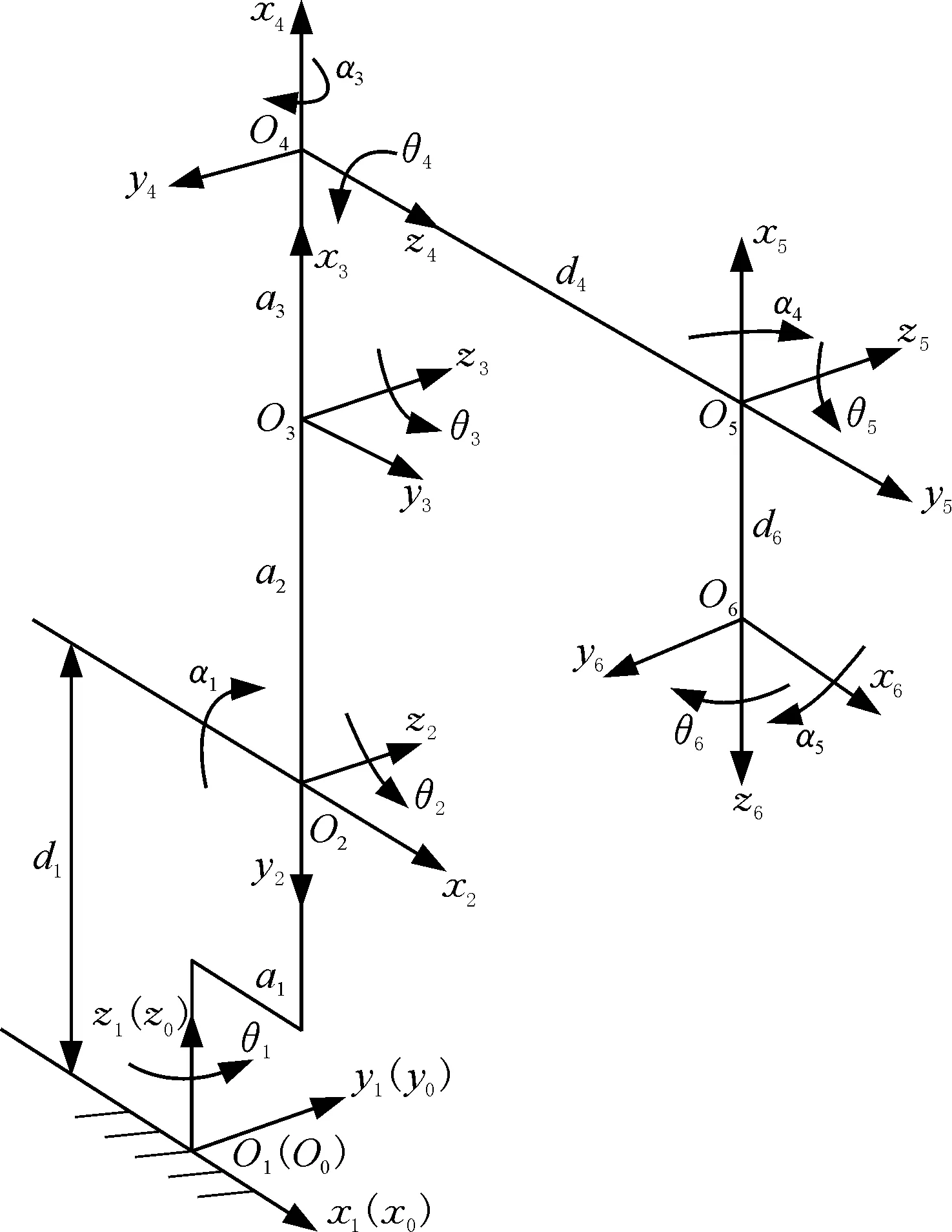
圖1 SR4C型工業(yè)機器人關節(jié)坐標系Fig.1 SR4C industrial robot joint coordinate system

如圖1所示，機器人相鄰兩個關節(jié)間坐標系的理論轉換矩陣可表示為

(1)

式中，i(i=1，2，…，6)為關節(jié)編號；ai為連桿長度；αi為連桿扭轉角；di為連桿偏移量；θi為關節(jié)轉角。

基于式(1)所示的關節(jié)坐標系轉換矩陣，將各關節(jié)轉換矩陣依次相乘，可以得到機器人末端坐標系{W6}(O6x6y6z6)相對于基坐標系{W0}(O0x0y0z0)的理論變換矩陣為

(2)

式中，(Px，Py，Pz)為機器人末端坐標系的原點在基坐標系下的位置坐標；(nx，ny，nz)T、(ox，oy，oz)T、(ax，ay，az)T分別為機器人末端坐標系x、y、z軸相對于基坐標系的方向余弦。

1.2 位置誤差模型

(3)

對式(1)進行全微分，并代入式(3)可得

(4)

式中，di為位置誤差向量；δi為姿態(tài)誤差向量; Δai為實際和理論連桿長度之間的偏差；Δαi為實際和理論連桿扭轉角之間的偏差；Δdi為實際和理論連桿偏移量之間的偏差；Δθi為實際和理論關節(jié)轉角之間的偏差。

將式(3)所示的相鄰關節(jié)坐標系的實際變換矩陣依次相乘，可以得到機器人末端坐標系相對于基坐標系的實際位姿矩陣為

(5)

式中，TN為機器人末端坐標系相對于基坐標系的理論矩陣；TD為機器人末端坐標系相對于基坐標系的位姿誤差矩陣。

令關節(jié)i到關節(jié)6的坐標系轉換矩陣依次相乘為Ui，其表達式如下：

(6)

式中，ni、oi、ai為姿態(tài)矩陣的3個3×1的列向量；Pi為3×1的位置向量。

由式(5)可得機器人末端坐標系相對于基坐標系的位姿誤差矩陣為

(7)

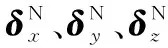
由式(7)可得到機器人的位置誤差模型為

(8)

式中，J為機器人的雅可比矩陣；Δq為待辨識的實際D-H參數(shù)與理論D-H參數(shù)之間的偏差；O1×3為1×3的零向量。

1.3 距離誤差模型

以位置誤差模型為基礎可以推導出機器人距離誤差模型，距離誤差向量關系如圖2所示。設機器人指令軌跡上選取的兩點為j點和j+1點，對應兩點之間的理論距離用sO表示。設指令軌跡上選取的兩點對應實際軌跡上的j′點和j′+1點，兩點之間的實際距離用sR表示。則指令軌跡兩點之間距離與實際軌跡兩點之間距離的差值可以表示為

Δs=sO-sR

(9)

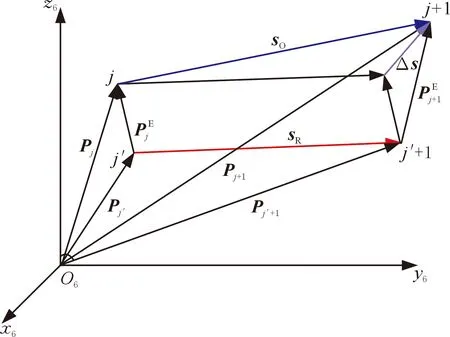
圖2 距離誤差向量關系圖Fig.2 Distance error vector diagram

由圖2所示的向量關系可得[15]

sOΔs≈|sO||Δs|

(10)

根據(jù)式(9)和位置誤差模型(式(8))可得到機器人的距離誤差模型為

(11)

式中，(xO(j+1)，yO(j+1)，zO(j+1))、(xO(j)，yO(j)，zO(j))分別為j+1點和j點在指令軌跡上的坐標；ΔxO(j+1)、ΔyO(j+1)、ΔzO(j+1)分別為j+1點在x、y、z方向的位置誤差；ΔxO(j)、ΔyO(j)、ΔzO(j)分別為j點在x、y、z方向的位置誤差。

在上述基本距離誤差模型中，空間隨機點之間的距離是不定值，為減少因兩點間距離誤差值差異過大而帶來的計算舍入誤差，本文研究給出基于球面選點的等距離誤差模型，以簡化模型和計算。在等距離誤差模型中，固定空間中一點為球心，將球心坐標設為(xc，yc，zc)，其余點處于以該點為球心、R為半徑的球體包絡面上，如圖3所示。由式(11)并結合式(8)可得等距離誤差模型為

Δs=

(12)

式中，Jj為j點對應的雅可比矩陣；Jc為球心對應的雅可比矩陣。

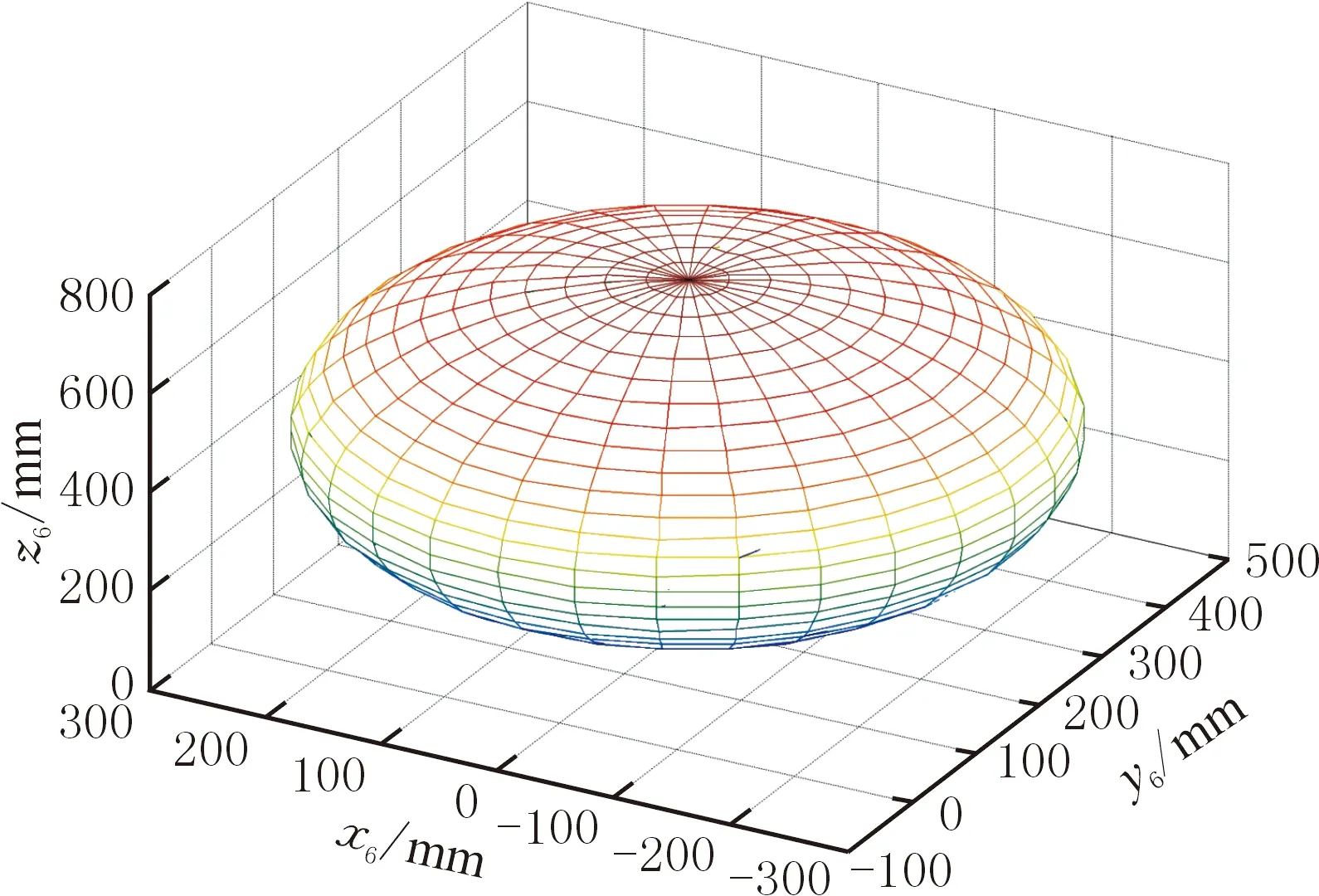
圖3 等距誤差模型采樣球面Fig.3 Isometric error model sampling sphere

當已知機器人位置誤差時，可由式(8)計算得出當前絕對定位誤差對應的D-H運動學參數(shù)誤差Δq。將所得到的Δq代入式(12)所示的等距離誤差模型中即可計算出對應的距離誤差，反之也可由距離誤差反推得到位置誤差，因此，機器人的距離誤差和絕對定位誤差有一一對應的關系，距離精度可以作為絕對定位精度的度量標準之一。

2 改進IGG3權函數(shù)的最小二乘辨識算法

將式(12)中除Δq以外的表達式用矩陣H來代替進行化簡，可得

Δs=HΔq

(13)

利用最小二乘法進行計算可得

Δq=(HTH)-1HTΔs

(14)

當觀測數(shù)據(jù)呈正態(tài)分布時，采用最小二乘法可以準確地求取Δq，但當觀測值中存在遠離數(shù)據(jù)群體的觀測值(即測量粗差值)時，這些粗差值對殘差平方和的影響要比其他觀測值對殘差平方和的影響大得多，從而會導致估計量受到嚴重影響，因此考慮使用抗差估計法來排除粗差值的影響。

極大似然估計法是抗差估計的常用方法，其原理為：利用已知的樣本結果反推最大概率導致這樣結果的參數(shù)值，得出極大似然估計量，可以盡可能地削弱粗差值對結果的影響。此處的樣本結果為Δs=(Δs1，Δs2，…，ΔsN)，參數(shù)值為Δq。首先建立極大似然函數(shù)：

l(Δq)=p(Δs1，Δs2，…,ΔsN|Δq)=

(15)

式中，p(·)為樣本結果Δs的概率密度函數(shù)；N為采樣點個數(shù)。

根據(jù)極大似然原理，固定樣本觀測值Δs1，Δs2，…，ΔsN，挑選參數(shù)Δq使得

max(p(Δs1，Δs2，…，ΔsN|Δq)

(16)

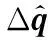
對式(16)等號兩邊取對數(shù)并整理可得

(17)

令ρ(Δsj，Δq)代替-ln(p(Δsj，Δq))，可得

(18)

計算中使用改正數(shù)vj(j=1,2,…，N)來衡量粗差大小，vj可表示為

vj=HjhΔqh-Δsj

(19)

其中，Hjh為矩陣H中第j行第h列元素，Δqh為Δq中第h個參數(shù)。則可將式(18)中ρ(Δsj，Δq)寫成ρ(vj)，可得

(20)

為求解出式(20)的極值，對其進行求導，可得

(21)

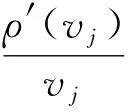
(22)

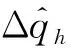
(23)

v=(v1，v2，…，vN)T

對式(23)變換可得

(24)

其中，P(v)為權函數(shù)矩陣，且為對角陣，具體形式為P(v)=diag(p1，p2，…，pN)。

將式(24)與標準最小二乘法得到的模型參數(shù)誤差計算公式(式(14))相比可知，基于抗差估計的最小二乘法與標準最小二乘法之間的差別為增加了一個權函數(shù)矩陣P(v)，即在計算最小二乘殘差平方和時給予每個殘差不同的權值以控制其在總體計算中所占的比重。

基于抗差估計的最小二乘法權函數(shù)矩陣通常采用IGG3權函數(shù)，IGG3權函數(shù)的表達式如下：

(25)

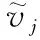
IGG3權函數(shù)的調和系數(shù)k0、k1根據(jù)正態(tài)分布標準差面積占總面積比值選取，正態(tài)分布中±1.5個標準差范圍內的面積占總面積的86.6%，該范圍內的觀測值應盡量保留；正態(tài)分布中±2.5個標準差范圍內的面積占總面積的98.7%，該范圍外的觀測值遠離樣本群體，應盡量剔除。綜上，k0常取值1.5，k1常取值2.5。

IGG3權函數(shù)的一階導數(shù)在k0處不連續(xù)，導致函數(shù)在k0處不平滑，則k0附近的可利用信息在抗差估計中得不到充分利用[16]，因此本文選用改進的IGG3權函數(shù)將殘差數(shù)據(jù)分為4段，以避開不可導的點，改進的IGG3權函數(shù)可表示為

(26)

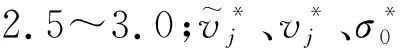
由于式(14)中(HTPH)-1矩陣為超定病態(tài)陣，外部微小擾動會影響參數(shù)值的結果，因此對式(24)進行嶺估計，其表達式如下：

(27)

其中，I為單位矩陣；α為嶺估計方法系數(shù)，取經(jīng)驗值0.01，用來避免出現(xiàn)(HTPH)-1矩陣的條件數(shù)過多且因(HTPH)-1矩陣接近病態(tài)矩陣而對微小擾動十分敏感的情況。

基于上述改進IGG3權函數(shù)距離誤差模型的機器人標定算法的標定流程如圖4所示，其中，qk為當前迭代過程的運動學參數(shù)，qk+1為后一次迭代過程的運動學參數(shù)。

圖4 距離誤差標定算法流程圖Fig.4 Flow chart of distance error calibration algorithm

算法的主要流程如下：將測量的實際位置值和機器人理論位置值及理論參數(shù)作為輸入，計算出距離偏差Δs，同時根據(jù)機器人距離誤差模型計算出對應的雅可比矩陣J，將二者代入基于改進IGG3權函數(shù)的最小二乘距離誤差辨識算法中進行參數(shù)辨識并迭代，根據(jù)設定的距離誤差閾值e和最大迭代次數(shù)Num進行判斷，當其中之一的條件滿足時便停止迭代，并輸出辨識結果，從而完成模型參數(shù)誤差的辨識。

3 實驗驗證與分析

3.1 實驗平臺的搭建

為分析與驗證所提出基于改進IGG3權函數(shù)距離誤差模型的工業(yè)機器人標定方法的有效性和可行性，構建了圖5所示的實驗系統(tǒng)，主要包括Leica AT960激光跟蹤儀、SR4C型六自由度機器人及其配套裝置等。激光跟蹤儀的測量精度為±10 μm，系統(tǒng)分辨力為0.1 μm，最大跟蹤速度為6 m/s；機器人工作范圍為0～672.8 mm，機器人的理論D-H參數(shù)將作為辨識算法的輸入代入計算，具體參數(shù)如表1所示。

圖5 實驗系統(tǒng)Fig.5 Experimental system

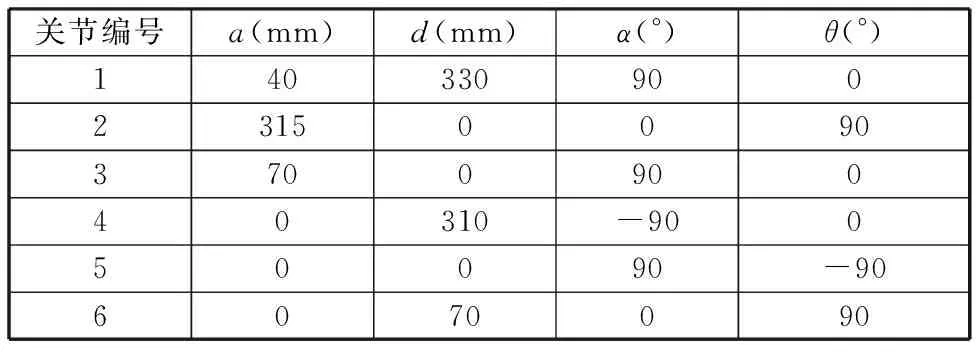
表1 機器人理論D-H參數(shù)表

3.2 辨識算法對比實驗

本文開展了辨識算法的對比實驗來驗證基于改進IGG3權函數(shù)距離誤差模型的機器人標定算法的有效性和可行性，具體步驟如下。

(1)在實驗前先將激光跟蹤儀開啟并預熱20 min，然后確定球心、球體半徑并規(guī)劃采樣點，如圖6所示。利用MATLAB中sphere函數(shù)將所生成的球面劃分成30×30個小網(wǎng)格，以便采樣點的選取，從已劃分的球面網(wǎng)格中均勻地選取50個采樣點。

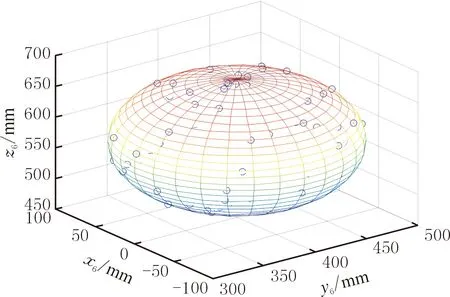
圖6 采樣點規(guī)劃Fig.6 Sampling point planning

(2)規(guī)劃好50個采樣點后控制機器人依次進行運動，利用激光跟蹤儀對采樣點進行測量。首先進行軌跡規(guī)劃，在機器人當前位置到第一個指令點之間采取關節(jié)空間梯形速度規(guī)劃；50個采樣點之間進行笛卡兒空間直線軌跡規(guī)劃，再通過機器人逆解算法及最小路徑算法將機器人笛卡兒空間坐標值轉換成關節(jié)坐標值再轉換成編碼值下發(fā)給控制器，每個采樣點位之間設置2 s停頓，以供激光跟蹤儀進行數(shù)據(jù)采集。

(3)將靶球固定于末端執(zhí)行器，在機器人作業(yè)的同時，通過跟蹤儀測量得到50個位置坐標。

(4)將測量得到的50組測量值和獲取的50組關節(jié)坐標值以及表1中的理論參數(shù)代入辨識算法中進行辨識，并得到一組新的D-H參數(shù)。

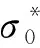
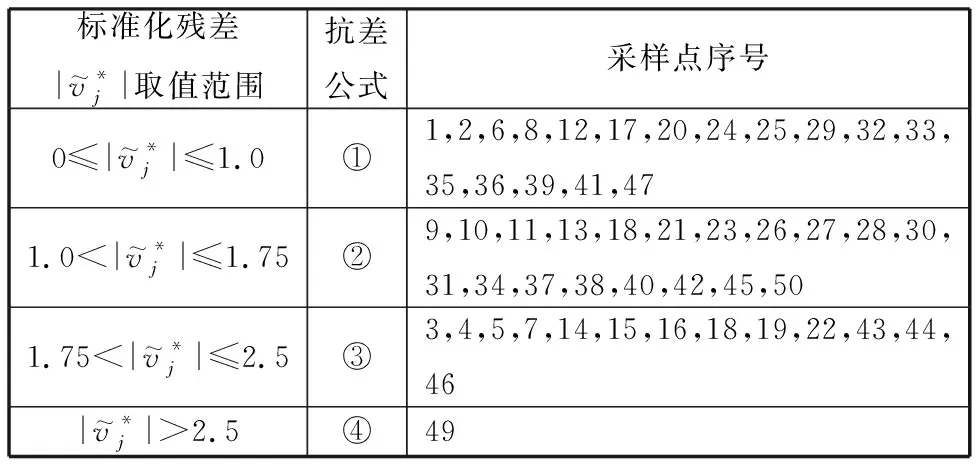
表2 抗差數(shù)據(jù)處理情況

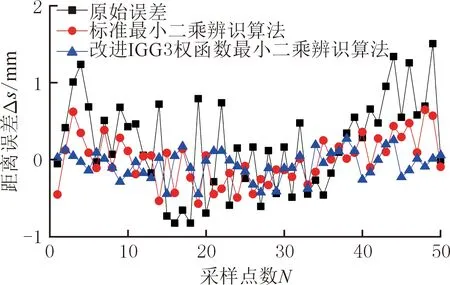
圖7 辨識算法比對實驗結果Fig.7 Comparison experimental results of identification algorithm

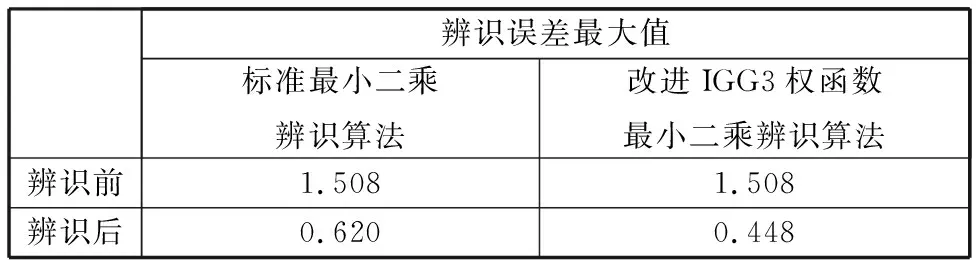
表3 標準最小二乘與改進IGG3權函數(shù)最小二乘辨識實驗結果

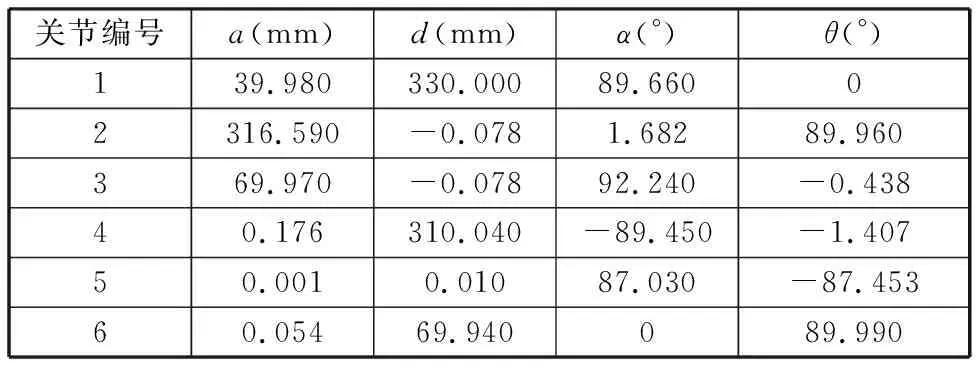
表4 改進IGG3權函數(shù)辨識D-H參數(shù)表

對比實驗結果表明：使用標準最小二乘辨識算法和改進IGG3權函數(shù)最小二乘辨識算法均可顯著地減小距離誤差值，且與標準最小二乘辨識算法相比，利用本文提出的改進IGG3權函數(shù)最小二乘辨識算法能更加有效地減小距離誤差值。

3.3 補償實驗

為驗證經(jīng)運動學參數(shù)誤差補償后的機器人定位精度，將辨識出的D-H參數(shù)表覆蓋原始理論的D-H參數(shù)表，重新對50個目標點進行誤差補償。機器人依次運行50個目標點，同時利用激光跟蹤儀進行測量，得到測量坐標點。根據(jù)機器人距離誤差模型公式，計算50個點到球心點的距離與標準半徑之間的差值，得到補償后的距離誤差值。選取半徑R=100 mm的球面采點，其補償前后機器人的距離誤差如圖8和表5所示。

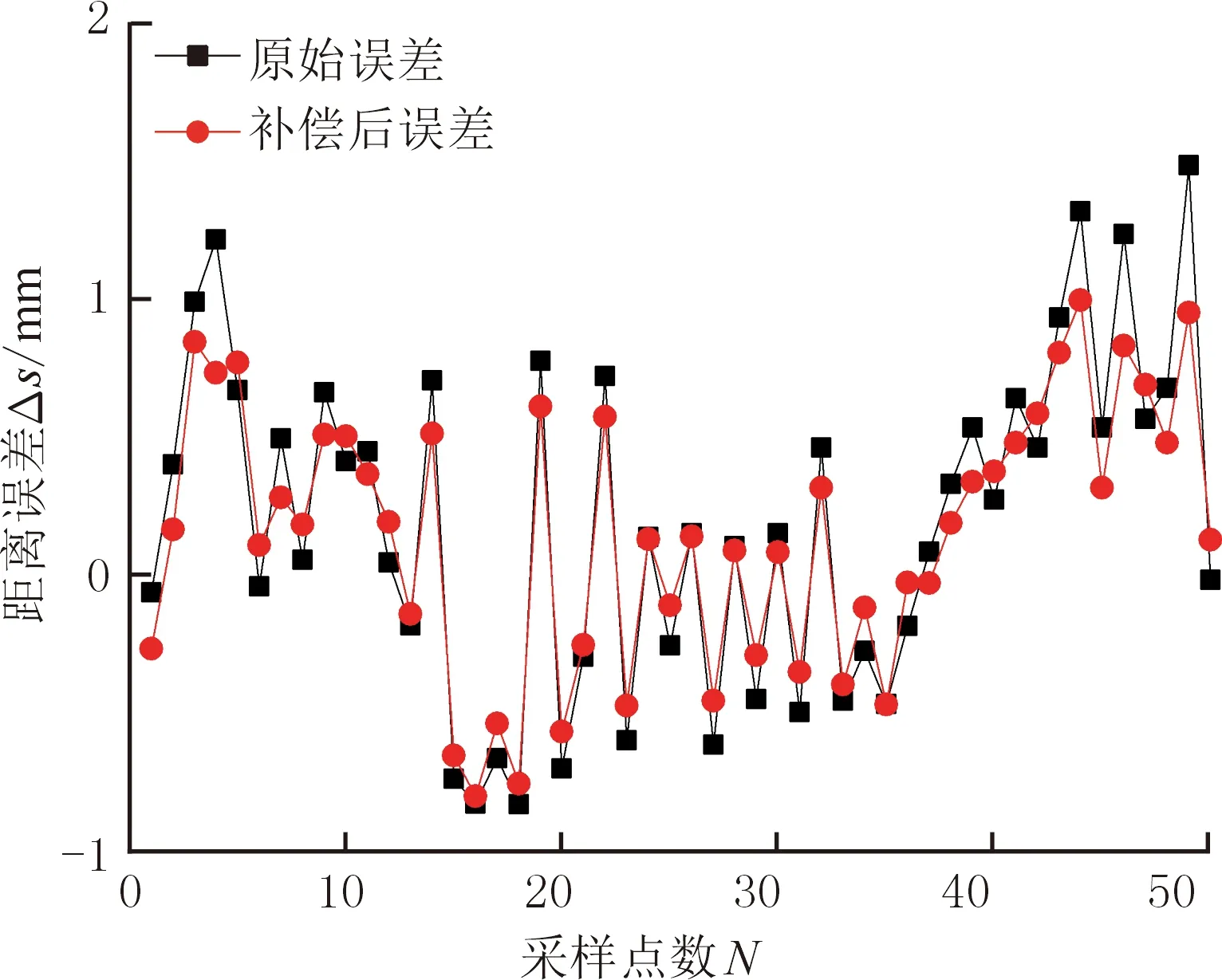
圖8 補償前后的實驗結果Fig.8 Experimental results before and after compensation

表5 距離誤差補償前后實驗結果

補償實驗結果表明：在R=100 mm的距離誤差補償實驗中，補償后的距離誤差值比補償前的距離誤差值減小了32.69%。

本次實驗研究對象為新松SR4C型工業(yè)機器人，是提供底層開發(fā)接口進行運動算法控制的實驗樣機，與商業(yè)用的機器人相比在正逆解算法精確度、軌跡規(guī)劃算法中速度平穩(wěn)性能方面仍存在不足，除運動學參數(shù)誤差導致的末端位置誤差之外，這兩方面因素也會極大影響機器人的末端定位精度。實驗結果表明，利用所提出的基于改進IGG3權函數(shù)距離誤差模型的辨識補償方法可減小距離誤差值，從而可提高工業(yè)機器人的精度。

4 結語

本文針對基于距離誤差模型的工業(yè)機器人標定方法在實驗過程中存在的粗差問題，提出了將改進的IGG3權函數(shù)最小二乘辨識算法用于距離誤差工業(yè)機器人標定中，以進一步提高工業(yè)機器人的標定精度。開展了改進IGG3權函數(shù)的機器人標定算法研究，基于SR4C型工業(yè)機器人構建了算法驗證和補償實驗系統(tǒng)，并開展了實驗研究。實驗結果表明：標定后的精度比標定前提高了32.69%，從而驗證了所提方法的可行性。本文研究的基于改進IGG3權函數(shù)距離誤差模型的工業(yè)機器人標定方法可用于工業(yè)機器人標定和校準領域，可為工業(yè)機器人定位精度的提高提供一定的理論和方法參考。