基于kNN發現社團主干的社團檢測算法

李 明，陳 梅，張 梅

(蘭州交通大學 電子與信息工程學院，蘭州 730070)

社團檢測可以發現復雜網絡中結構或功能相似的模塊[1]，對復雜網絡進行社團檢測可以揭示網絡隱含的結構和潛在的功能，有極為重要的現實意義[2].研究人員提出了大量的社團檢測算法，主要有基于模塊度[3]、基于標簽傳播[4]、基于隨機游走[5]和基于相鄰節點關系[6]的社團檢測算法.基于模塊度的方法有追求模塊度最大化的Fast Q[3]算法；基于標簽傳播的方法有根據節點鄰居更新節點標簽的LPA(label propagation algorithm,LPA)[4]算法；基于隨機游走的約束游走過程的Synwalk[5]算法；基于節點間關系的社團檢測算法有Black Hole[7]算法、DA(a divide and agglomerate algorithm,DA)[8]算法和棒不打鴛鴦[6]算法.

由于基于節點間關系的社團檢測算法可以從網絡的拓撲結構層面發現社團結構[8]，近年來，研究人員提出了大量該類的社團檢測算法.基于節點間引力與斥力的Black Hole算法通過得到使得整個網絡合力最小的分布來檢測社團結構；基于全局局部關系的DA算法側重于同時從全局和局部角度考慮檢測社團結構，并在分配無類標節點時利用節點間的影響力對其進行分配[9]；棒不打鴛鴦算法則從“兩個互近鄰節點極有可能屬于同一個社團”出發生成樹狀圖并剪枝檢測社團結構.然而，當需要檢測任意結構任意規模的網絡時，這些算法就難以檢測到準確的社團結構了.

為了檢測任意結構任意規模的社團，本文提出了一種簡單、高效和時間復雜度低的基于k最近鄰發現社團主干的社團檢測算法DCCB.DCCB算法的核心在于：它根據相似節點對及其kNN(knearest neighbors,kNN)鄰居生成的社團主干進行聚類，并利用互kNN連接的關系對社團主干進行擴展，克服了棒不打鴛鴦算法僅從一個社團核心出發的局限性.此外，DCCB利用kNN擴展社團主干，這種方法認為社團內所有節點都以互kNN方式相連，這使得DCCB算法能不受社團結構和規模限制，檢測出正確的社團主干；得到社團主干后，檢測異常節點，并將其標記為無類標節點；分配無類標節點時，借鑒DA算法的無類標節點分配模式，使用節點間影響力分配無類標節點即可得到最終的社團結構.

1 相關定義

1.1 網絡的定義

網絡G可表示為G=(V,E).其中V表示節點集，E表示邊集.記|V|為n，表示網絡節點數.記|E|為m，表示網絡邊數.若G中?xi,xj∈V，?(xi,xj)?E，?(xj,xi)?E且滿足(xi,xj)=(xj,xi),則該網絡中的邊沒有方向，那么稱圖G為無向網絡(undirected network).對于網絡G，若?(xi,xj)?E，則節點xi與節點xj為鄰居節點.通常，對于網絡中的一個節點xi，定義它的鄰居集合為N(xi)，將節點xi鄰居的個數|N(xi)|稱為節點的度，記作dxi.

1.2 相鄰節點之間的相似度

本文采用Jaccard相似度[10]計算兩個節點xi與xj的相似度，如公式(1)所示，公式(1)中|coc(xi,xj)|表示節點xi,xj之間公共鄰居的個數.

(1)

1.3 k最近鄰

x1,x2,…,xi,…,xn是節點集V中的n個節點.對G中的每個節點xi∈V，與xi最相似的k個鄰居被稱為xi的k最近鄰,表示為Nk(xi)，Nk(xi)?V.

1.4 互k最近鄰

給定節點集V中的兩個點xi與xj，當且僅當xi∈Nk(xj)且xj∈Nk(xi)時，稱xi與xj為互k最近鄰 (mutualknearest neighbors,MkNN).如果xi和xj沒有出現在另一個點的k最近鄰中，xi與xj就不是互k最近鄰，也就是不存在互k最近鄰關系.

1.5 共享k最近鄰

對于節點xm，如果節點xi和xj為MkNN，且滿足xm∈Nk(xi)和xm∈Nk(xj)，xm就是xi與xj的共享k最近鄰(sharedknearest neighbors,SkNN).

1.6 吸引力

在社團中，存在一些影響力大的核心節點.2019年Li Z團隊[9]提出了傳播者的概念，將該類節點稱為傳播者，可通過傳播者對其它節點的影響對無標簽節點進行合理分配.本文定義節點xi對節點xj的吸引力為gravity(xi,xj)，如公式(2)所示，其中Jaccard(xi,xj)可由公式(1)計算.在處理無標簽節點時，可以通過計算吸引力對該節點進行合理分配.

gravity(xi,xj)=dxi·Jaccard(xi,xj).

(2)

2 基于kNN發現社團主干的社團檢測算法

本節將對DCCB算法進行詳細敘述.首先敘述提出該算法的動機并給出算法整體流程圖；然后詳細敘述該算法的核心部分，即基于kNN合并社團主干；接著描述無標簽節點的分配；最后對該算法的時間復雜度進行分析.

2.1 動機

通過認真研究網絡的社團結構，可以發現網絡中互為近鄰且相似度很高的一對節點極有可能在一個社團中.這里以圖1中所示的空手道社交網絡[11]進行舉例說明，該網絡右側社團中的“1”號節點和“2”號節點互為近鄰且相似度較高.這對節點就是核心節點，該社團中的其余節點都與核心節點存在互近鄰關系.這些核心節點與人際關系中的領袖類似，即一個團體中其余的人或多或少受領袖的影響，這對核心節點與核心節點的鄰居組成的小社團就是社團主干.受此啟發，提出了基于相似近鄰節點發現社團主干的算法DCCB；該算法首先利用互k最近鄰找到相似度較高的一對節點，接著將這對節點及他們的共享k最近鄰作為社團主干，這樣可以最大可能地找到與他們相似的節點，即這兩個人的共同朋友；最后通過互近鄰擴展社團主干，利用網絡中節點的相似性以及近鄰關系進行社團檢測.

圖1 空手道社交網絡Fig.1 Karate Network

2.2 算法流程圖

本節將對算法的具體流程進行闡述.圖2(a)為DCCB算法的整體流程圖，圖2(b)為基于kNN合并社團主干的具體流程.

圖2 算法流程圖Fig.2 Algorithm flow chart

2.3 基于kNN合并社團主干

在識別社團主干時，DCCB算法只需一個輸入參數k，即最近鄰個數.開始尋找社團主干時，該算法首先從一個從未訪問過的節點xi開始遍歷，若xi存在互k最近鄰xj，則將xi、xj以及它們的共享k最近鄰節點集合在一起去生成初始的社團主干.若xi不存在互k最近鄰，則將xi單獨當作一個社團主干，在檢測異常節點時再處理.這種互kNN的連接方法使得DCCB能夠發現任意互k最近鄰節點所組成的社團.該種方法生成的社團主干受社團結構規模影響較小，可以盡可能的將相似的節點及與它們聯系緊密的鄰居節點劃分到同一個社團中去.社團主干所屬的社團一般由一個或多個社團主干構成，若兩個社團主干之間存在重疊的節點，則說明這兩個社團主干屬于同一個社團，應當合并.找到所有社團主干后，用吸引力可輕易的將社團中其余節點劃分到與它有鄰居關系的社團主干中去，得到最終的社團結構.

為了更直觀明了的展示該過程，將對該過程進行可視化描述，具體步驟如圖3所示.圖3(a)表示初始網絡，該網絡由3個小網絡構成.圖3(b)中，從節點“0”出發，找到該節點的互k最近鄰節點“1”，然后發現該節點對的共享k最近鄰節點“3”，就找到了該社團的主干.圖3(c)中，從節點“1”出發，找到該節點的互k最近鄰節點“3”，然后發現該節點對的共享k最近鄰節點“2”.此時，由于節點“1”和節點“3”在已有社團主干中，將節點“2”加入到該社團主干中.圖3(d)中，繼續通過社團主干的合并將節點“4”納入進去，即得到第一個社團的社團主干.圖3(e)中，由于節點“5”沒有互k最近鄰節點，將該節點擱置.圖3(f)與圖3(g)中，則采用與找第一個社團主干同樣的方法找第二個社團主干.最終，通過kNN合并社團主干，得到了正確的社團主干，如圖3(h)所示.

圖3 社團主干的生成Fig.3 Generation of the community backbone

2.4 異常點檢測及無標簽節點的分配

DCCB算法識別社團主干時，會將不存在互k最近鄰的單個節點，包含2個節點及1個共同鄰居的3個節點作為社團主干加入到已有社團主干中.生成社團主干時若該類節點無法吸引外部節點，則說明該類節點不是社團主干，需要重新劃分.DCCB算法檢測異常節點時，將包含節點數小于3的社團主干中的節點分配到無類標節點中重新劃分.

DCCB算法在進行無類標節點的分配時，借鑒了LPA算法以及LGM&GM[9]模式.該模式認為節點的影響力與節點度的大小成正比，度越大影響力越大，綜合考量節點的度以及兩個節點間的相似性，提出了節點間的吸引力.在分配時，首先利用公式(2)找到對無類標節點吸引力最大的鄰居節點，然后將該無類標節點劃分到鄰居節點所在社團主干，得到最終的社團結構.

2.5 時間復雜度分析

DCCB算法計算k近鄰時，用“k-d tree”實現，時間復雜度為O(n·logn)，其中n為節點集V中節點的個數.計算k近鄰與形成社團主干時間復雜度為O(n·k)，其中n為圖中節點的個數，k為每個點最近鄰個數，由于k?n，這2個步驟時間復雜度可近似的認為是O(n).

檢測異常節點時查找包含節點小于等于3的社團主干時間復雜度為O(n).劃分無類標節點的時間復雜度為O(z·davg)，z表示無類標節點數，davg表示節點的平均度.由于davg?z，分配無類標節點的時間復雜度為O(z).整個算法時間復雜度為O(n·logn+n+n+z)，由于O(z)和O(n)時間復雜度相當，且n?n·logn，所以DCCB的時間復雜度為O(n·logn).

3 實驗結果與分析

為了檢驗DCCB算法能否檢測出不同結構不同規模的社團，本節實驗選取了4個便于可視化展示的不同結構的真實網絡以及3個不同規模的人工合成網絡[12]，并與常見的5個社團檢測算法進行了對比，驗證了DCCB算法的有效性及正確性.

3.1 數據集及對比算法

本節的實驗使用了表1所示的4個真實網絡數據集和3個人工合成網絡數據集.4個真實網絡數據集是空手道俱樂部網絡(Karate)、游戲地圖網絡(Risk map)、海豚社交網絡(Dolphins)和大學生足球聯賽賽程表網絡(Football)[11].這些網絡都是公開發布的真實數據集，網絡規模較小，結構各異，便于可視化處理，能直觀的展示實驗結果.此外，這些網絡的真實結構都已知，便于進行指標量化處理，評估不同算法的檢測結果.3個不同規模的人工合成網絡數據集由LFR(a lancichinetti,s fortunato,f network,LFR)測試網絡生成工具程序生成[12]，分別包含2 000，5 000和20 000個節點.這些網絡的統計信息如表1所列.

表1 實驗所用數據集Tab.1 Networks used in the experiment

LFR人工合成網絡需指定參數.為了測試DCCB算法在不同規模社團上的效果，生成了L_2k與L_5k數據集；為了測試DCCB算法在大規模網絡上的表現，生成了L_20k數據集；這些數據集參數設置如表2所列.在這些參數中，混合系數μ很關鍵，若μ>0.5，則生成的社團結構趨于模糊，檢測困難；若μ<0.5，則生成的社團結構很清晰，易于檢測.由于實驗需要驗證DCCB算法在不同規模網絡上的效果，這3個網絡混合系數μ設置為0.4即可.

本文選取5個典型的社團檢測算法作為對比算法，包括模塊度最優算法(Fast Q，FQ)[3]、典型的標簽傳播算法LPA[4]算法、經典的譜聚類算法(Spectral Clustering,SC)[13]、新型的基于節點間作用的算法(Attractor,Att)[14]以及基于吸引力模式的算法(Black Hole,BH)[7].為了更直觀的看出算法在數據集上的表現，本文采用了2個常用的評價指標，即歸一化互信息量(normalized mutual information,NMI)和調整蘭德指數(adjusted Rand index,ARI)來對不同算法做統一衡量.對于不穩定的算法，評價指標取運行30次該算法結果的平均值，結果圖為檢測到的社團結構評價指標最高的一次.

3.2 真實網絡的結果分析

3.2.1 Karate網絡的結果分析

圖4展示了DCCB與5種對比算法在Karate數據集上的社團檢測結果.從圖4中可以看出，Fast Q算法，Spectral Clustering算法以及Black Hole算法檢測效果不佳，未能得到清晰良好的社團劃分.DCCB算法、Attractor算法表現良好，能得到質量較高的社團結構.DCCB算法除了將節點32劃分錯誤外，其余節點都被正確地劃分到了相應的社團.圖4(c)是LPA在Karate上最好的檢測結果，該次結果錯誤地劃分了節點3，但從表3可以看到該算法多次得到的結果評價指標平均值較DCCB算法差.Fast Q算法和Black Hole算法表現較差，SC算法錯誤地劃分了節點3、節點20和節點14.Attractor算法除了將節點10劃分錯誤外，其余的節點都劃分正確.Black Hole算法將網絡劃分為4個社團.

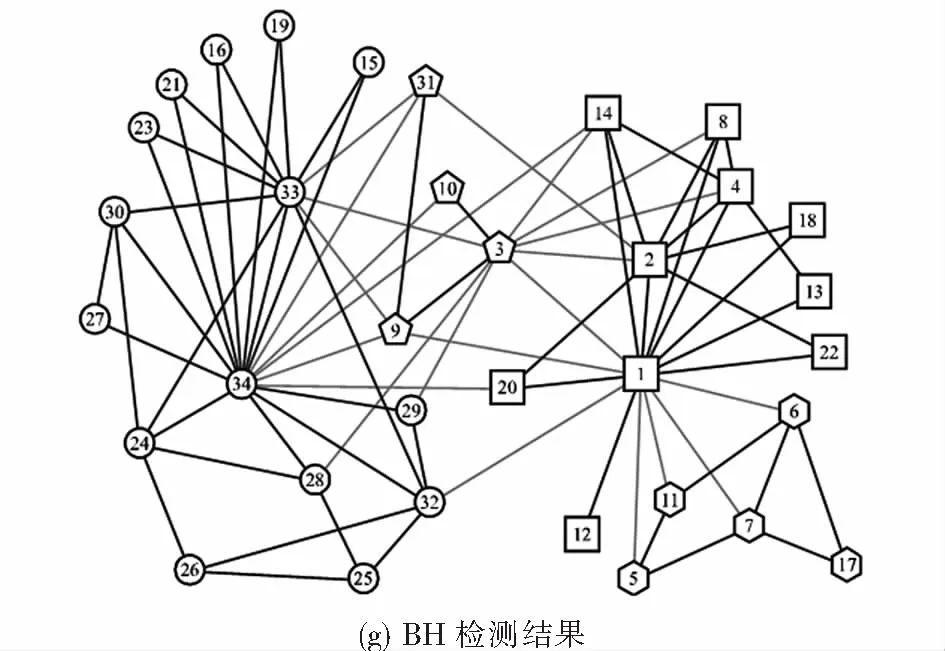
圖4 Karate網絡上的檢測結果Fig.4 Detection results on Karate network

3.2.2 Risk map網絡的結果分析

圖5展示了DCCB與5種對比算法在Risk map數據集上的聚類結果.可以從圖5(b)明顯看到：DCCB算法除了將節點26劃分錯誤外，其余節點都被正確地劃分到了相應的社團，且成功檢測了右上角較難檢測的2個社團.從表3也可以看到，DCCB得到了最高的ARI和NMI值，較其它5個對比算法劃分的社團結構更準確.從圖5可看出，算法LPA、Fast Q和Spectral Clustering分配的結果都不太理想，未能成功地檢測出良好的社團結構.網絡右側的兩個社團比較難檢測，基于互近鄰的DCCB在該網絡表現良好，可以檢測出該社團.

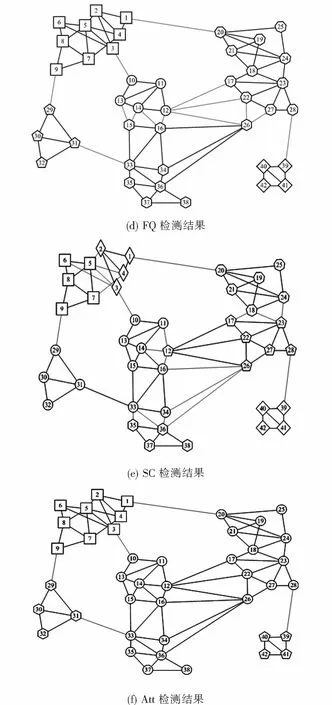
圖5 Risk map網絡上的檢測結果Fig.5 Detection results on Risk map network

3.2.3 Dolphins網絡的結果分析

圖6展示了DCCB與5種對比算法在Dolphins數據集上的聚類結果.圖6(a)是Dolphins的真實社團結構，圖6(b)為DCCB算法的社團檢測結果.該網絡結構比較復雜，難以檢測.從圖6與表3可以看出，大部分算法在該網絡上表現不太好，但DCCB仍然能檢測出高質量的社團結構，且比其它5個對比算法檢測出的結果更優.通過圖6(c)可以看出，LPA算法、Fast Q算法、Spectral Clustering、Attractor以及Black Hole算法在Dolphins數據集上的實驗結果并不理想，得到的社團結構與真實的社團結構有很大偏差.從表3可以看到，DCCB得到了最高的ARI和NMI值，較其它5個對比算法劃分的社團結構更準確.從圖6(b)可以看到，DCCB算法除了將社團邊緣的3個節點8、40及60分配錯誤外，其余節點均分配正確.

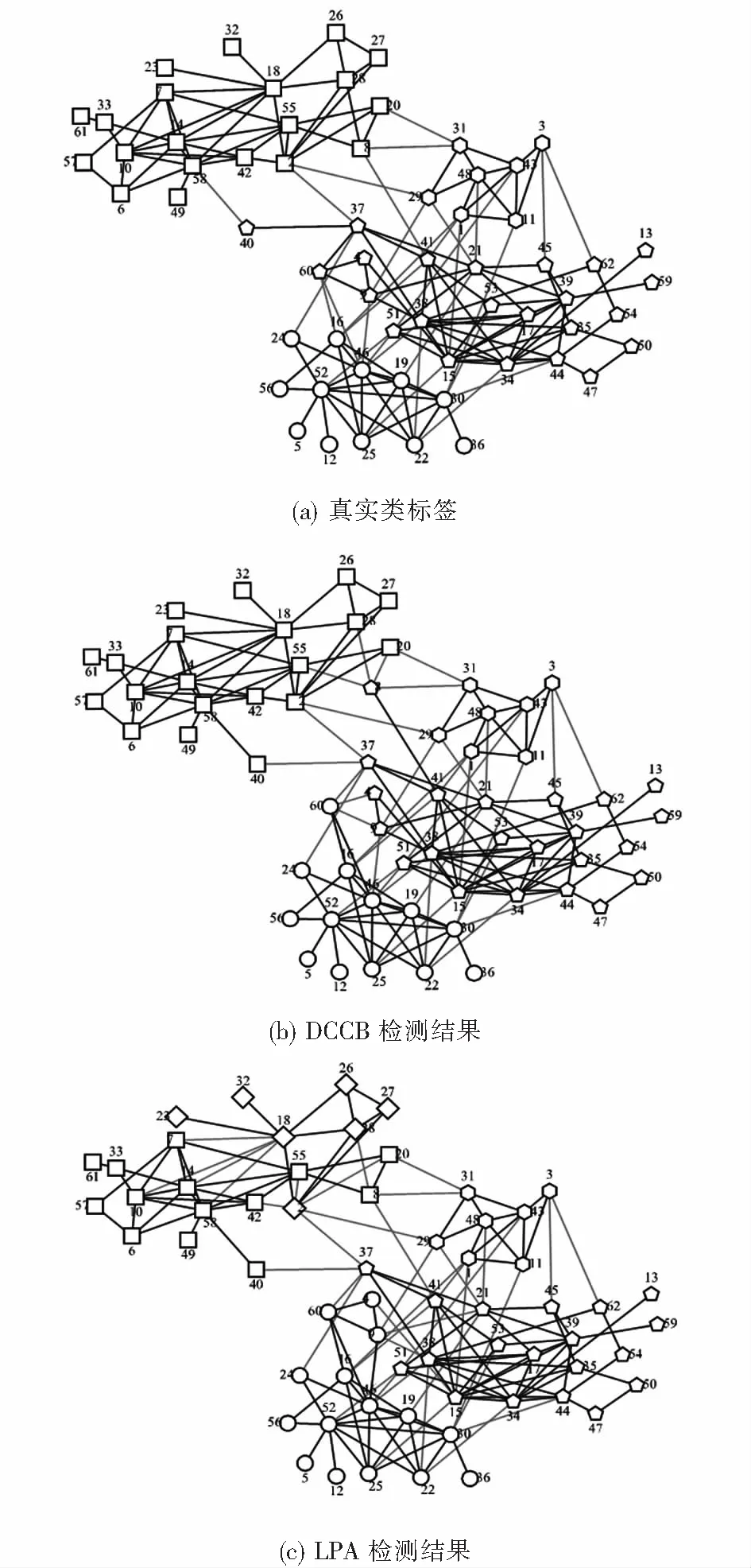
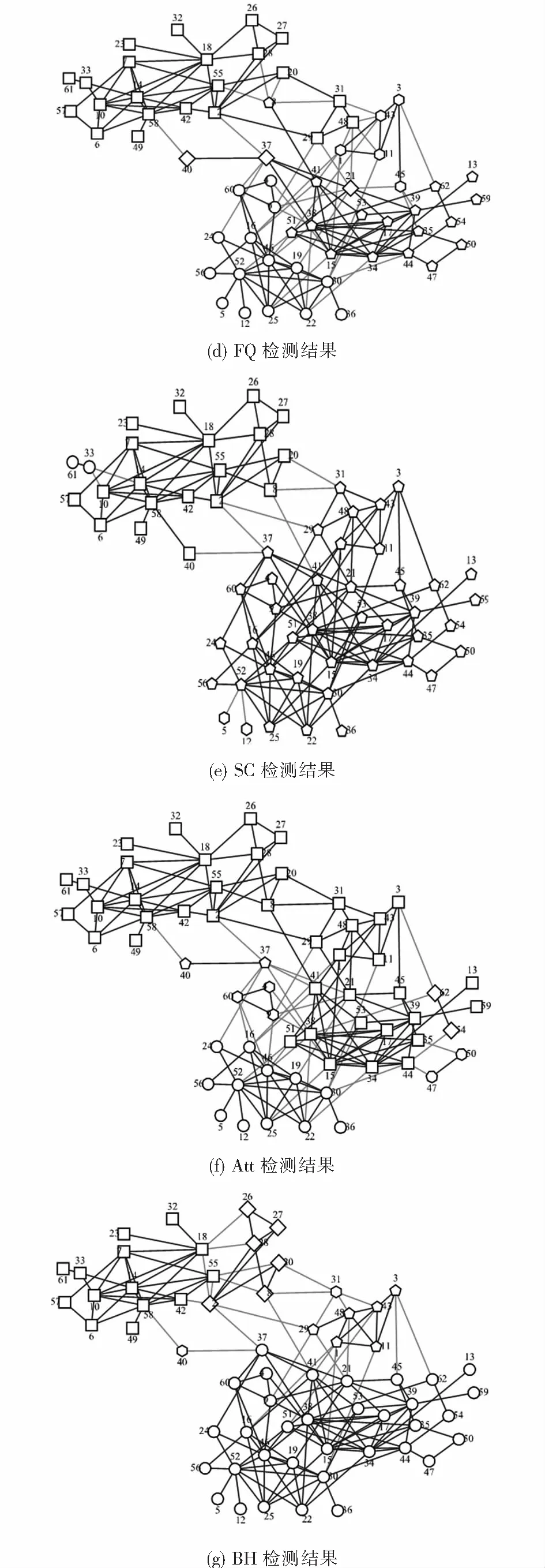
圖6 Dolphins網絡上的檢測結果Fig.6 Detection results on Dolphins network

3.2.4 Football網絡的結果分析

圖7展示了DCCB與5種對比算法在Football數據集上的聚類結果.圖7(a)是Football的真實社團結構，圖7(b)為DCCB算法的社團檢測結果.DCCB除了將中間的一個包含4個節點的小社團錯誤劃分到左上角社團外，其余部分的社團結構完全正確.Attractor算法劃分時也錯誤地將左上角社團的一個節點劃分給該小社團.從表3可以看出，Attractor算法、DCCB算法以及Black Hole算法在該網絡表現良好，其余幾個算法在該網絡表現較差.

圖7 Football網絡上的檢測結果Fig.7 Detection results on Football network

表3 多個有真實標簽網絡數據集檢測結果比較Tab.3 A comparison of detection results on the various network datasets with ground truth

3.3 LFR網絡的結果分析

L_2k數據集有2 000個節點，包含103個社團.從表3可以看出，在該網絡上，DCCB方法得到的ARI及NMI均為最大，識別出了完全正確的社團結構.Attractor算法的結果與其相同，Black Hole算法、LPA算法的結果與其比較相近但稍差于DCCB算法，Fast Q算法及Spectral Clustering算法的ARI和NMI均低于DCCB算法.其中，Attractor算法在運行L_5k和L_20k時出現內存錯誤，未能得到結果.L_5k數據集有5 000個節點，包含219個社團，從表3可以看出，在該網絡上，DCCB檢測到的社團結構的ARI是最高的，其它的社團檢測算法除了LPA和Black Hole外社團檢測結果并不理想.Black Hole算法在不同數據集上均有良好的表現，在L_5k數據集的結果比DCCB更好.L_20k參數設置與L_5k保持一致，該網絡有20 000個節點，包含219個社團，從表3可以看出，DCCB在該網絡上的ARI和NMI均為最高，較其它算法表現好.LFR網絡上的實驗結果表明DCCB能很好的檢測出不同規模的社團.

3.4 算法的時間復雜度比較

優秀的算法應有較低的時間復雜度[15-17].Spectral Clustering時間復雜度O(n3)；Fast Q的時間復雜度為O(n2)；LPA的時間復雜度為O(n)，但該算法結果不穩定且準確度很差.Attractor算法時間復雜度為O(m+am+Tm)，其中：a為兩節點間外部鄰居的平均數；T為迭代次數.Black Hole算法的時間復雜度為O(n·logn).DCCB的時間復雜度為O(n·logn).總體來說，DCCB時間復雜度較低，且能得到較準確的社團結構.

3.5 總體分析

為量化分析DCCB算法以及其它5個算法的效果，選取了兩個社團檢測中最常見的評價指標ARI、NMI對社團檢測結果量化分析，結果如表3所示.除了在Football數據集上較Attractor算法稍差，在L_5k數據集上較Black Hole算法稍差，在其余5個數據集上，DCCB檢測到的社團質量較其它算法都好.對不同算法在不同數據集上的量化評價指標ARI、NMI取均值，如圖8所示，很明顯DCCB算法取得的ARI、NMI均值是最高的，優于其它算法.此外，本節還采用盒圖作為可視化統計方法，對算法的表現進行評估，如圖9所示.在7個數據集上，對于ARI、NMI這兩個評價指標，DCCB算法在四分位數、中位數、最大值及最小值均有著優秀的表現.L_2k以及L_5k人工合成網絡的實驗表明，DCCB可以準確識別出不同規模的社團.L_20k數據集上的實驗表明，DCCB在規模較大數據集上發揮穩定，可以檢測到高質量的社團劃分.綜上所述，DCCB是一個簡單、時間復雜度較低、結果穩定且能在不同結構不同規模網絡中檢測到高質量社團結構的社團檢測算法.

圖8 DCCB及對比算法在不同數據集上ARI，NMI均值比較Fig.8 A comparison of average ARI,NMI on the various network datasets with DCCB and contrast algorithms

圖9 具有真實社團結構網絡上的ARI，NMI盒圖Fig.9 Box plots of ARI,NMI on the networks with ground-truth community structures

4 結論

本文提出了一種基于kNN發現社團主干的社團檢測算法，在4個不同結構真實網絡和3個不同規模的人工合成網絡進行實驗，并與5個常見的社團檢測算法對比，得到以下結論：

1) 基于kNN發現社團主干的社團檢測方法可有效解決現有的社團檢測算法不能很好的檢測出任意結構任意規模社團的問題，且該算法時間復雜度較低，提高了社團檢測效率.

2) 本文提出了通過互kNN連接發現社團主干的方法，該方法具有良好的應用價值和適用性，對于社團檢測及聚類的相關研究，都有良好的借鑒價值.

3) 在實驗過程中，發現該算法合并社團主干時容易混淆社團邊界處的節點.可通過引入目標函數的方法對社團主干的合并過程進行約束，來得到準確度更高的社團結構.