光子氣體量子相變對原子衰減率的影響
王英, 張建軍, 楊國暉
山西師范大學物理與信息工程學院, 山西 臨汾 041000
0 引言
BEC是玻色體系在低溫時出現的一種宏觀集聚現象,其顯著特征是:低于某一特定溫度時,所有粒子集聚到空間最低能態[1~3].我們知道光子是玻色子,理論上光子可實現BEC[4,5].但光的BEC卻很難在實驗上觀察到,困難在于光子無質量且化學勢為零[6,7].直到最近,J. Klaers等人通過將激光限制在由凹面鏡包圍的薄腔內,克服了這個困難[8].受此啟發,本文構建了一個二維非線性光學微腔,并考慮:光的量子相變會對原子衰減率產生什么影響?
1 模型和哈密頓量
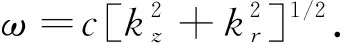
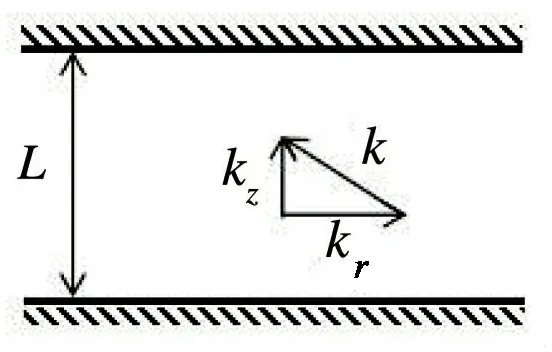
圖1 微腔模型:該微腔由兩個高反射率的鏡子組成Fig.1 Microcavity model:the microcavity consists of two mirrors with high reflectivity
(1)
這里有效光子質量意味著在這二維光學微腔中光子可看作是一般玻色子.此外,微腔中光子源不斷發射和吸收光子,確保了總光子數守恒,也暗示系統化學勢非零.我們知道對于一般玻色子,在低溫極限下系統存在宏觀集聚現象,對于我們現在的光子系統而言,這一特性應該也幸存.進一步,我們考慮微腔中充滿非線性介質,由于非線性效應,我們知道光子在微腔中也能夠耦合為光子對.
因此,在低溫極限下,我們引入下面唯象的哈密頓量來描述當前系統:
H=HBEC+H′
(2)
這里
HBEC=-μ(a+a+b+b)+Uaaa+a+aa+Uaba+b+ba-g(b+aa+H.c.)
(3)
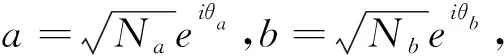
(4)
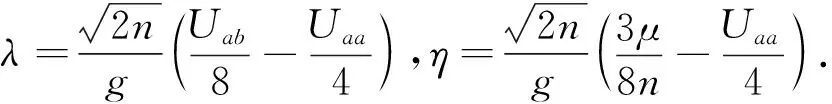
(5)
其中,μeff=η-λ是光子氣的有效化學勢,-1 在純光子對凝聚相,H′具有如下形式: (6) (7) H′最終變為 (8) (9) 我們知道,一直以來光與原子的相互作用情況都是研究的重點,在目前的模型中,我們考慮將一二能級原子置于微腔中,設該原子的激發態、基態分別為:|a〉、|b〉,將它放入受體腔,描述光與原子的相互作用哈密頓量為 (10) (11) 其中Δ=ωc-ωk,ωc是原子基態與激發態的玻爾轉變頻率.這里(11)式第一項表示原子吸收一個聲子并從基態|b〉躍遷到激發態|a〉,第二項表示相反過程.上式結果說明:在低溫下,由于光子BEC,原子和弱相互作用光子場的耦合變為原子和非相互作用聲子場的耦合. 聲子系統在微腔中可看作是一個源,受體腔中的原子可看作是一個小系統,因此可用源理論來分析原子衰變.在Weisskopf-Wigner 近似下[12]我們發現微腔中原子的約化密度算符具有形式 (12) ΓN=(N-αT2)-3/2 (13) (14) 其中H′由(8)式給出.由于不同模式的準粒子算符相互對易[13],由熱力學公式[14],可得系統的自由能 (15) 將(15)式的求和化為積分,得系統相對自由能 (16) 這里v(Tc)與v(T)由(9)式給定,由(16)式我們發現,隨著系統溫度的升高,系統自由能增大,這一結果意味著系統變得不太穩定,有更多的粒子參與到與光子的相互作用中,因此原子的衰減率也相應增加. 在這篇文章中,我們構建了一個由光子和光子對組成的二維微腔模型,在這個模型中,光子的有效質量和化學勢不會消失,這也意味著現在的光子氣體存在BEC凝聚相.我們也研究了微腔中二能級原子的衰減率,結果發現:系統溫度足夠低時,大量粒子集聚在單一量子態,使自由能最小化.之后,隨著溫度的升高,自由能變大,系統變得不穩定,更多的粒子參與到系統相互作用中,于是原子衰減率也越來越大. 圖2 衰減率隨相對溫度的變化Fig.2 Change of decay rate with relative temperature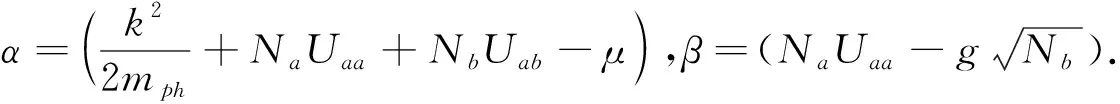
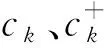
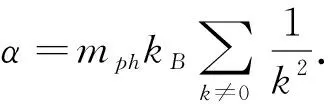
2 原子衰減率
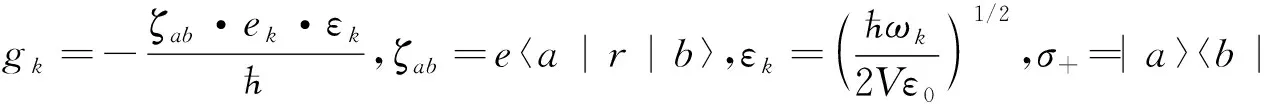
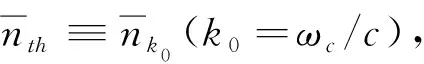
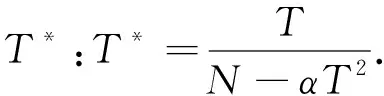
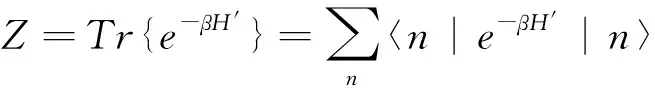
3 結論