基于測井參數優選的煤層含氣量預測模型

陳 濤，張占松，周雪晴，郭建宏，肖 航，譚辰陽，秦瑞寶，余 杰

(1.長江大學 地球物理與石油資源學院，湖北 武漢 430100；2.油氣資源與勘探技術教育部重點實驗室(長江大學)，湖北 武漢 430100；3.中海油研究總院，北京 100027)

近年來，隨著非常規油氣勘探的興起，國內外對于煤層氣的勘探研究一度成為相關領域的研究熱點，其中煤層含氣量是整個煤層氣儲層評價研究的核心參數之一，是關乎煤層氣開發等一系列生產布局的關鍵所在。目前，國內外已有不少研究學者對煤層氣儲層含氣量的預測評價有了一些成果性的認識，同時也得到了較為廣泛的應用，其中，最為經典的煤層含氣量預測方法是Langmuir 方程，于1992年由J.M.Hawkins 等學者提出[1]，核心思想是構建煤的工業組分與Langmuir 參數間的映射關系，建立模型計算煤層含氣量。在眾多提出的煤層含氣量預測方法中，最為直接可靠的方法是煤心實驗，通過實驗測試直接獲得準確的煤層含氣量數據，然而該方法存在的最大問題是難以實現大面積取心實測進而不能滿足工業生產的需求，且煤心實驗測試經濟成本較大。此后，為彌補煤心實驗分析獲取煤層含氣量方法的不足，大量學者相繼提出基于煤質、測井參數等多元回歸方法構建煤層含氣量預測模型[2-7]。隨著近些年研究的不斷深入，研究者們深入挖掘測井參數中隱藏的豐富地質信息，利用測井資料可有效解決煤層含氣量預測問題。起初一些學者通過構建測井參數與煤層含氣量之間的線性回歸方程實現煤層含氣量預測[8]，后來發現這樣的線性回歸方法過于簡單，難以滿足高精度預測的要求。

隨著機器學習及人工智能等技術的發展，各研究領域的專家學者開始將機器學習等技術引入自身研究領域以解決科研問題，此時，有些學者開始將機器學習技術應用于煤層含氣量預測中，目前最具代表性的是BP 神經網絡、灰色模型、支持向量機以及隨機森林[9-14]，研究成果已經表明這些技術的引入可以有效改善煤層含氣量預測問題。然而，對于機器學習建模應用，影響模型性能最為核心的因素當屬建模自變量的選取，不同的研究問題，建模自變量及網絡結構不盡相同，即使不同的研究區，測井參數與煤層含氣量以及各測井參數間的隱含關系也存在很大差異，利用機器學習方法構建預測模型時，選擇的測井參數不佳將嚴重影響模型整體的預測性能，導致預測精度損失，進而不足以滿足當前煤層氣勘探對于煤層含氣量的高精度預測需求。基于此，本研究提出基于測井參數優選的煤層含氣量預測模型，首先通過簡單的線性相關分析明確煤層含氣量的測井響應特征，基于MIV(Mean Impact Value)方法實現測井參數優選，考慮到支持向量機對于小樣本數據體的建模效果更為可靠，本研究選用支持向量機算法作為核心建模技術，但其存在核心參數選擇問題，給定的常用參數值并不一定是本研究問題的最佳參數，為此，本文同時引入仿生優化算法(粒子群算法)對支持向量機的核心參數進行尋優，以此在建模的每個關鍵環節上做最優化處理，進而構建穩健、強魯棒性的煤層含氣量高精度預測模型。

1 煤層含氣性測井響應特征

1.1 數據來源

目前，作為我國石炭–二疊紀煤炭儲量最大的煤田，沁水煤田不僅產煤量巨大，其煤層含氣量也非常豐富，占我國煤層氣儲量的近25%，截至目前，在我國的煤層氣資源勘探區中，沁水煤田的勘探和開發程度最高，且煤層氣儲量穩定性條件最佳，將在未來很長一段時間內成為我國煤層氣勘探開發以及工業生產的主力區，最新的煤層氣儲量評價數據表明，該區的煤層氣資源儲量高于1×1012m3，未來的煤層氣開發前景非常可觀[15]。

本研究選取位于沁水煤田柿莊南區的126 塊煤心取樣測試的煤層含氣量數據以及對應各取樣點的常規測井數據，表1 為本研究的基礎數據，即126組樣本數據(部分展示)，每組數據包含煤層含氣量和測井參數。

表1 樣品含氣量及常規測井參數數據(部分)Table 1 CBM content of samples and conventional logging data(part)

1.2 測井參數相關性分析

常規測井參數中蘊含著大量的地質地層信息，有效地利用測井技術可以解決諸多的地質及儲層評價問題，不同的地質儲層情況具有不同的測井響應特征，煤層富含有機碳及煤層氣，具有其特殊的巖石物理信息，其含氣性具有特殊的測井響應特征，為具體分析煤層含氣性的測井響應特征，首先通過皮爾遜相關系數分析各常規測井參數與煤層含氣量間的相關性，同時計算測井參數彼此間的相關系數，據下式可計算得到各參數間的相關系數(表2)。

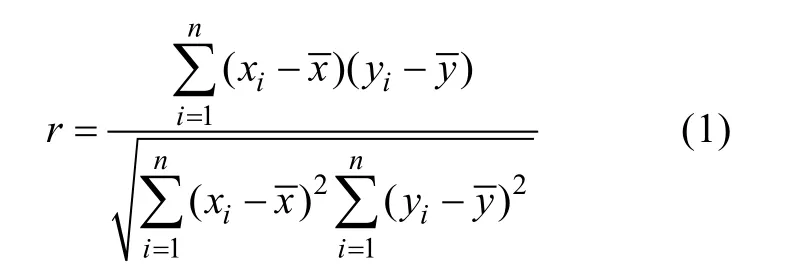
式中：r為皮爾遜相關系數；分別為測井曲線均值；xi、yi為第i個樣本對應的測井曲線數值。

由表2 中的相關性結果可知，不同的測井參數與含氣量間具有不同程度的相關性，且各測井參數間也存在相關性。為更直觀地顯示測井參數及含氣量間的相關情況，通過圖1 展示的相關系數熱圖可見，不論是測井參數彼此間還是測井參數與含氣量間的相關系數大小均存在較大的差異，基于測井參數建模對于測井參數的優選非常必要，測井參數間的相關性將嚴重影響模型性能，過多的冗余信息很可能給模型帶來噪聲。

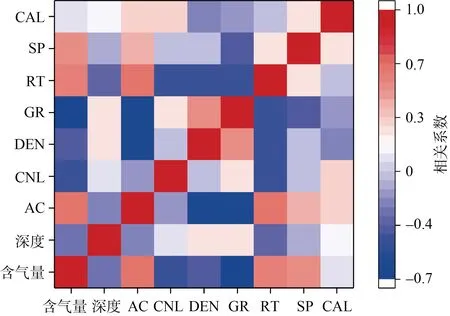
圖1 含氣量及常規測井參數相關性熱圖Fig.1 The heat map of correlation between gas content and conventional logging parameters

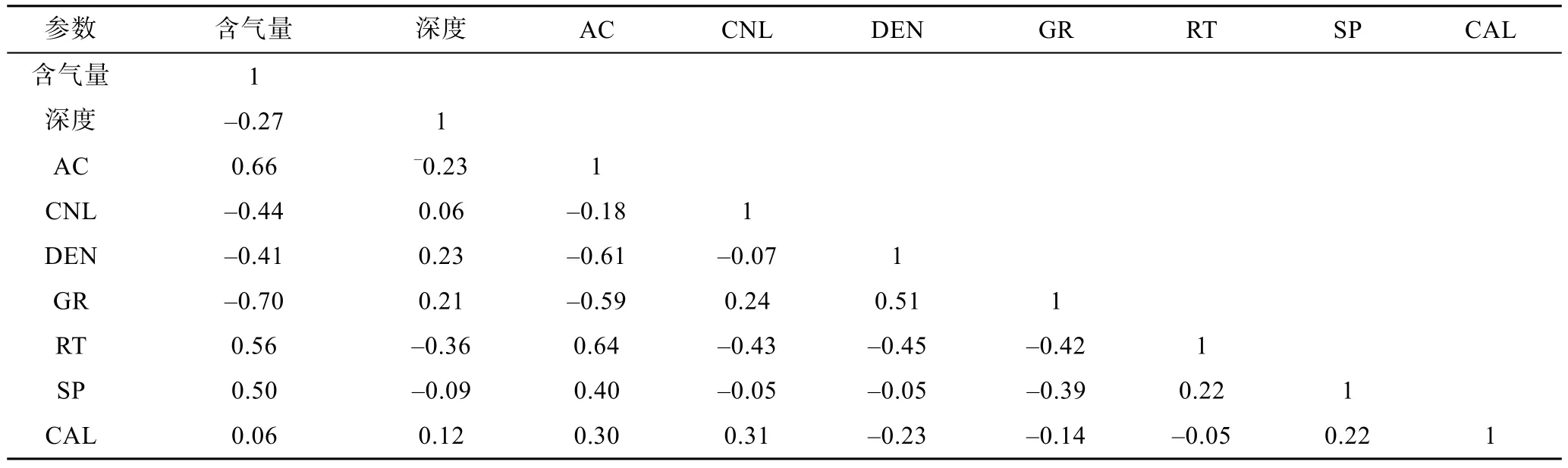
表2 煤層含氣量與測井參數之間相關系數Table 2 The correlation coefficients between CBM content and well logging parameters

基于上述的相關性分析，結合巖石物理性質，簡要做以下煤層含氣量測井響應特征分析：

①煤層的埋藏深度會很大程度影響煤化程度且間接影響煤層生烴量，即煤層埋深越深，在一定程度上推動著煤層氣產量[16]，但最終的煤層含氣量與后期的封閉條件密切關聯，從本研究的126 個取心樣本含氣量與深度的相關分析結果可見，煤層埋深與其含氣量存在負的弱相關關系，可見深度對于煤層含氣量的預測評價不可作為一個穩定的自變量，兩者關系受地區地質條件影響程度較大。

② 聲波時差測井值與地層巖石骨架及其孔隙充填物的物性密切相關，煤層內部結構相對松散，因而在煤層中傳播的聲波速度相對較低，時差較大，吸附或者部分游離在煤層中的煤層氣對聲速的影響更為敏感，煤層氣的存在致使聲波速度衰減，即導致聲波時差增大，煤層含氣量與聲波時差測井曲線呈正相關關系。

③在煤層中，儲層實際孔隙率通常較低，但煤層中地層水含量較高，加之煤層由碳、氫、氧的有機質組成且煤層氣成分以甲烷為主，使得煤層相較于圍巖中子測井表現為高值異常。理論上來說，煤層煤化程度升高，固定碳含量升高，煤層氣相對增多，那么含氣之后的煤層測量中子測井值相對增大，經補償后相對減少。但補償中子測井受井內流體礦化度、煤質組分中子骨架值及井內流體礦化度等一系列因素的影響。實際煤層含氣量與補償中子的線性回歸分析得出，補償中子與煤層含氣量呈負相關性。

④ 一般來說，密度響應值隨著煤(巖)層致密程度的增加而增大。相對于其他巖石，煤具有低密度特性，煤層氣主要以吸附態賦存于煤層中，煤層孔隙越豐富，其致密程度越小。煤層吸附含氣量相對越大，煤巖密度越低，煤層含氣量越大，密度越低，二者表現為負相關關系。

⑤ 煤巖骨架自身具有低放射性特點，其放射性強弱取決于煤的演化過程中的其他物質組分，如泥巖、黏土含量等，當煤層中富含黏土礦物時，自然伽馬測井表現出相對高值異常，但此時煤層的吸附能力受到削弱，致使煤層中含氣量降低，所以煤層含氣量與自然伽馬測井通常會表現出一定的負相關關系。

⑥ 富含煤層氣的煤巖礦化程度與圍巖呈現出高值異常，在擴散和吸附作用下，鉆井液和地層層間水之間的電位差劇增，自然電位測井與煤層含氣量之間呈正相關關系。煤層氣屬于非導電介質，致使煤層電阻率增高，煤層孔隙相對越豐富，煤層含氣量越大，煤層電阻率越大，煤層含氣量與電阻率測井響應呈正相關關系。井徑測井曲線與地層的機械強度密切相關，煤機械強度相對較弱，通常表現為井眼擴徑，煤層富氣，一定程度上增強了擴徑現象，但煤層的機械強度主要還是取決于煤巖骨架，所以煤層含氣量與井徑測井表現為弱正相關關系。

2 建模方法

通過上述煤層含氣量測井相關性分析，表明煤層含氣量與測井參數間存在隱含的函數映射關系，不同的測井參數與煤層含氣量的響應程度差異較大，且各測井參數間也存在一定程度的相關性，所以，在利用測井參數作為網絡建模時，應當充分考慮測井參數變量間的相關性，簡單的測井參數選取對于建立煤層含氣量預測模型非常不利，為此，本研究引入適合神經網絡建模的自變量優選技術，通過該優選策略以期建立最優化的預測模型。

2.1 最小二乘支持向量機(LSSVM)

SVM 是一種新型機器學習方法[17]。SVM 在統計學習理論基礎上，采用結構風險最小化原則，提高了對小樣本數據的泛化能力，較好地解決了神經網絡訓練時間長、訓練結果存在隨機性和過學習等缺陷，普遍應用于復雜非線性建模問題[18]。

LSSVM 是一種SVM 的衍生方法[19]，它將最小二乘估計成功引入SVM 中。與標準SVM 的不等式約束和求解二次規劃問題相比，LSSVM 選擇誤差平方項為優化目標，將等式約束作為約束條件，求解的是線性方程問題，簡化了運算過程，提高了計算速度和精度。本文采用的是LSSVM 的回歸形式，經過一系列嚴格推導與簡化，最后轉化為利用最小二乘法求解線性方程組中的α和b，得到LSSVM的回歸函數為：

式中：K(x,xi)為低維空間映射到高維空間所用的核函數。

2.2 粒子群算法(PSO)

粒子群算法(Particle Swarm Optimization，PSO)是一種全局最優化算法[20]，該方法基于對鳥群覓食過程的模擬，利用個體之間的間接通信來尋找最優解。

在D維解空間中，將每個優化問題的可能解看作空間中的一個“粒子”，由m個粒子組成一個群落，定義xi=(xi1,xi2,…,xiD)為粒子i的當前位置；vi=(vi1,vi2,… ,viD)為粒子i的當前飛行速度；pi=(pi1,pi2,…,piD)為粒子i到當前迭代為止所經歷過的最優位置。整個粒子群到當前迭代為止所搜索到的最優位置為pg=(p g1,pg2,…,pgD)。各個粒子追隨最優位置在解空間中進行搜索，則粒子i速度和位置的更新方程為：

2.3 測井參數優選

簡單的線性相關分析結果不足以為神經網絡建模提供輸入自變量優選支撐，因為測井參數與煤層含氣量間的關系非常復雜，且表現為隱函數關系，測井參數間的多重共線性對于建模也會產生干擾，所以有必要引入一種適用于網絡建模的自變量優選技術，即MIV(Mean Impact Value)方法，它由G.W.Dombi 等提出，通過計算出的MIV 數據可有效反映輸入自變量對于因變量的影響，數值大小直接可以衡量自變量對因變量的建模影響程度，該方法自提出以來受到了相關學者的廣泛認可及應用[21-23]。

MIV 方法的核心思想為通過控制單一變量原則，分別對每一個自變量數據做等比例縮放，計算自變量數據放大和縮小情景下的模型輸出結果之差，記為該自變量的MIV 值，按照該方式遍歷所有的自變量，得到所有自變量對因變量的影響程度，即MIV 值。

綜上，利用 MIV 技術優選測井參量，選擇LSSVM 網絡建立針對本研究的小樣本問題實現網絡建模，考慮到LSSVM 中核心參數人為設定的影響，采用仿生算法PSO 優化LSSVM 的核心參數，通過此三者的聯合，建立適用于煤層含氣量預測研究模型的流程(圖2)。

由圖2 可知，本研究流程主要分為3 個部分，首先對原始數據進行預處理(包括測井曲線標準化、煤心深度歸位、擴徑校正以及高灰、不符合測試規定及夾矸煤樣的數據清洗)，利用MIV 技術結合LSSVM網絡計算各建模輸入自變量的MIV 值，根據計算結果優選最佳建模自變量組合；LSSVM 涉及2 個關鍵核心參數，人為給定勢必帶來一定誤差，模型難以達到最佳性能，通過PSO 算法對LSSVM 網絡的正則化參數(c)以及高斯核函數寬度參數(σ)做全局尋優，最后基于最優輸入自變量組合和最優核函數參數(c、σ)構建適用于煤層含氣量預測的MIV-PSO-LSSVM模型。此外，由于測井參數具有不同的量綱和量綱單位，需要通過數據的歸一化處理消除建模自變量之間的量綱影響，所以，在通過MATLAB R2020a 編程實現本研究的整個建模過程中需要對建模數據做預處理(數據的歸一化處理)工作。

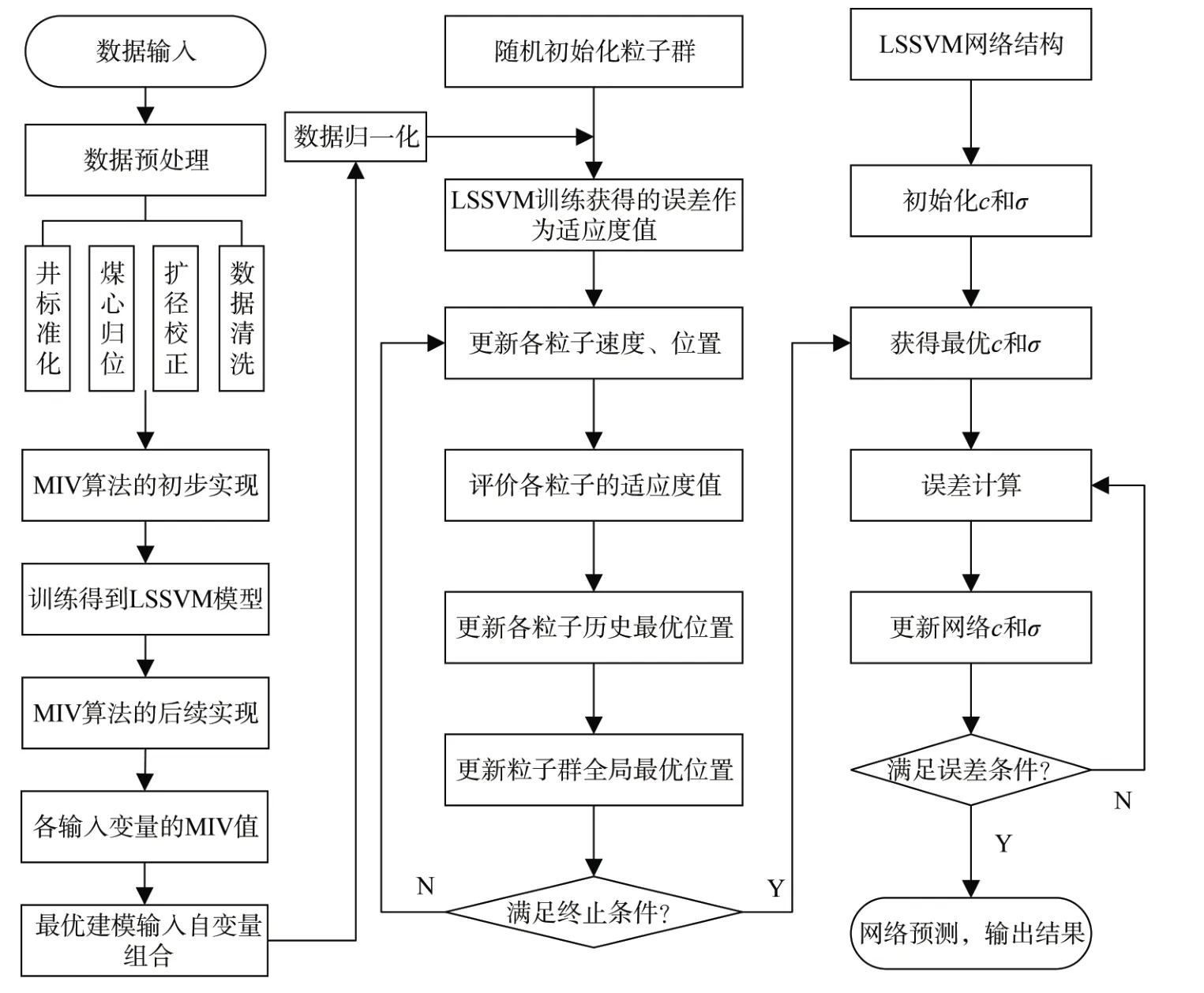
圖2 MIV 自變量優選下的PSO-LSSVM 建模流程Fig.2 The modeling flowchart of PSO-LSSVM under independent variable optimization by using MIV technology

3 模型構建及性能分析

3.1 模型構建

根據MIV 方法，分別對各常規測井參數計算分析其對煤層含氣量建模預測的影響，為有效優選出適用于本研究的網絡建模自變量，隨機生成4 組白噪聲數據作為自變量進行對照，圖3 為各自變量的MIV 值。參數對應的MIV 絕對值越大，表明該參數對因變量的影響程度越大，自變量與因變量間的函數關系越強，通過對照白噪聲下的MIV 值可將對輸出因變量影響程度非常弱的自變量(接近于白噪聲)放棄，視為無效參數，反之，視為有效參數。為進一步檢驗該優選參數方案的有效性，對有效和無效參數做假設檢驗，統計分析結果見表3，可知二者存在顯著性差異。選擇適用于網絡建模的最佳測井參數自變量組合，最優的測井參數包括AC、CNL、DEN、GR 和RT。

表3 有效參數組與無效參數組的MIV 絕對值(±s)分布Table 3 The MIV absolute value distribution of effective parameter group and invalid parameter group(±s)

表3 有效參數組與無效參數組的MIV 絕對值(±s)分布Table 3 The MIV absolute value distribution of effective parameter group and invalid parameter group(±s)

注：經t 值檢驗，兩組差異顯著(P<0.05)。

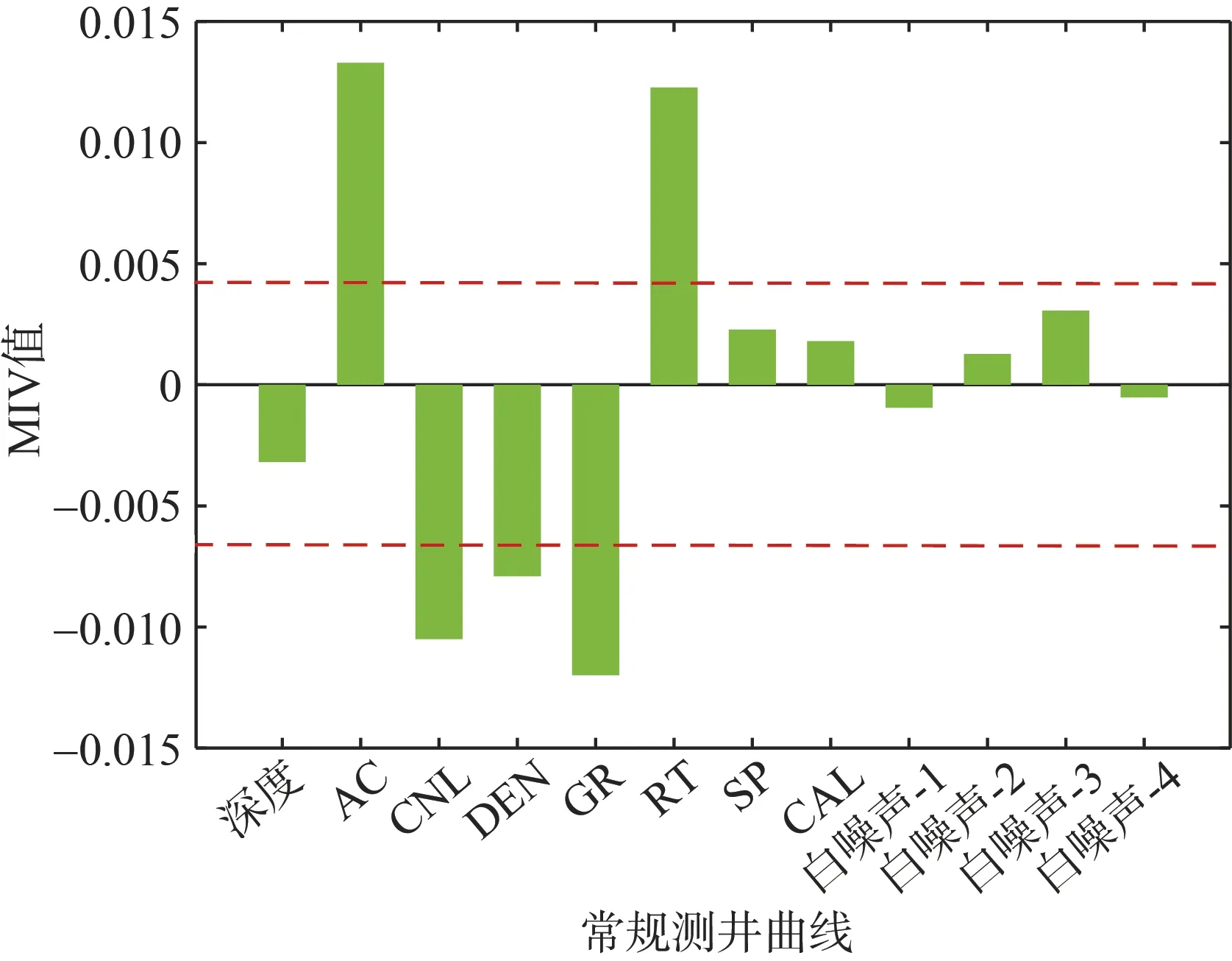
圖3 各測井參數對含氣量建模預測的影響Fig.3 Influence of logging parameters on modeling and prediction of CBM content

優選的參數作為建模自變量進行網絡建模，首先，利用LSSVM 方法建立測井參量與煤層含氣量間函數映射模型，輸入自變量(xi)和輸出因變量(yi)分別代表測井曲線和煤層含氣量。

由LSSVM 方法建立的測井參數與煤層含氣量之間的非線性模型結構為：

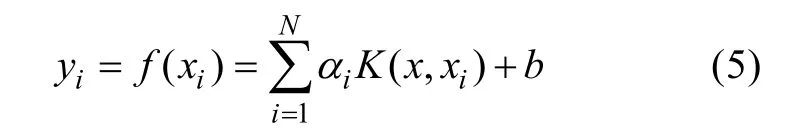
神經網絡核函數對于特征向量矩陣參數的選取較為苛刻，容易造成核矩陣病態化，且核參數的確定很大程度上依賴于先驗知識；高斯徑向基函數相比多項式核函數迭代次數少，運行效率相對高，只需確定一個核參數[24]。本研究選用高斯徑向基函數(RBF)作為模型的核函數，其表達式如下：

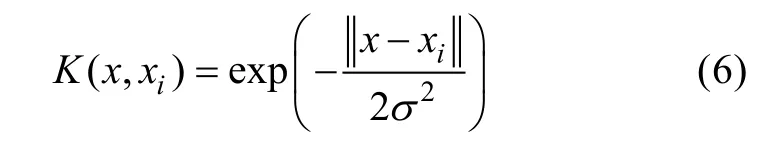
式中：x為核函數的中心；σ2為核函數的寬度參數。

通過PSO 算法求取結構風險計算式中的正則化參數c和式(6)中的核函數寬度參數σ。據圖2 可知，本研究需要對PSO 參數初始化，具體情況見表4。

表4 PSO 初始化參數Table 4 Initialization parameters of particle swarm optimization

圖4 為PSO 對LSSVM 的核心參數(c、g)全局尋優可視化，可見，通過 PSO 算法可有效實現LSSVM 核心參數的最優化，進而規避人為經驗法給定核心參數帶來的建模誤差。本研究尋優獲取的c和g最優值分別為2.71、0.18。根據核心參數尋優結果建立的LSSVM 模型，即為PSO-LSSVM 模型。

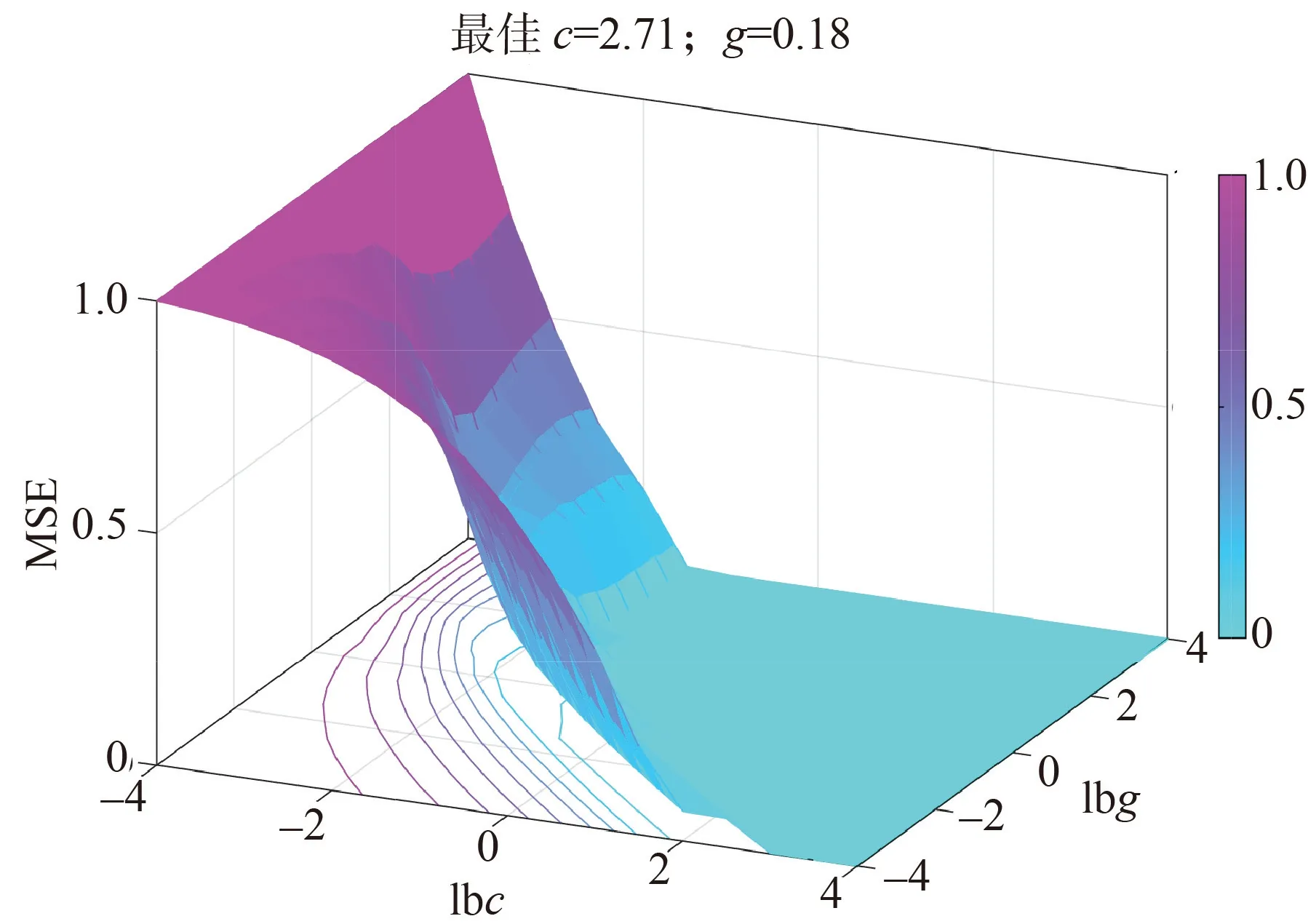
圖4 PSO 的尋優可視化Fig.4 Visualization of particle swarm optimization

3.2 模型性能分析

為進行建模效果對比分析，基于所有可用的常規測井參數分別建立LSSVM 模型以及帶粒子群算法優化的PSO-LSSVM 煤層含氣量預測模型，建模過程中將126 組樣本數據隨機分為訓練集和測試集，其中訓練集占比75%，剩下的樣本作為測試集。圖5 為LSSVM 模型及其PSO 優化下的煤層含氣量預測結果與實測含氣量的交會圖，可見不論是測試集還是訓練集，采用PSO 算法優化的LSSVM 模型的預測精度均優于LSSVM 模型，足見采用核參數尋優策略可有效改善神經網絡的建模性能，提高模型的預測精度。

為分析優選測井參數下的建模效果，選用上述MIV 方法優選的測井參數作為建模自變量分別建立LSSVM 模型以及PSO 優化下的LSSVM 模型，圖6為建立的模型在訓練集和測試集的預測結果與對應的實測煤層含氣量交會圖。從圖6 中可以看出，基于MIV 也證實了過多的冗余自變量反而會損害建模精度，網絡建模時存在的測井參數間的互相關性問題通過優選測井參數可以得到有效解決。對比圖5 與圖6 可知，LSSVM、PSO-LSSVM 模型在優選參數作為建模自變量后的模型預測精度有了大幅度提升，基于MIV 建模自變量優選的PSO-LSSVM預測性能最佳。

圖7 為基于多元線性回歸建立的煤層含氣量預測模型，可見多元線性回歸模型的預測性能在數據不均衡時效果不是很理想，與圖5、圖6 對比可知，基于機器學習算法建模對于反演測井參數與煤層含氣量間隱含的復雜非線性映射函數關系非常有效，遠優于簡單的多元線性回歸法建模。

圖5 LSSVM 模型及其PSO 優化下的預測結果與實測含氣量的交會圖Fig.5 The cross plot of prediction results and measured gas content

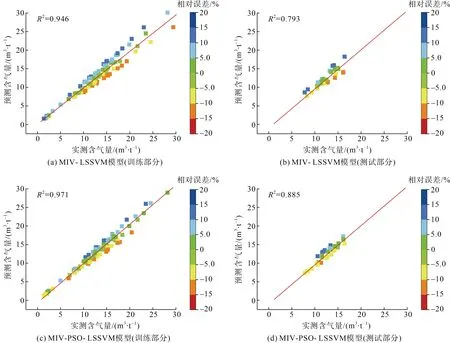
圖6 基于MIV 測井參數優選的LSSVM 模型及其PSO 優化下的預測結果與實測含氣量的交會圖Fig.6 The cross plot of prediction results and measured gas content

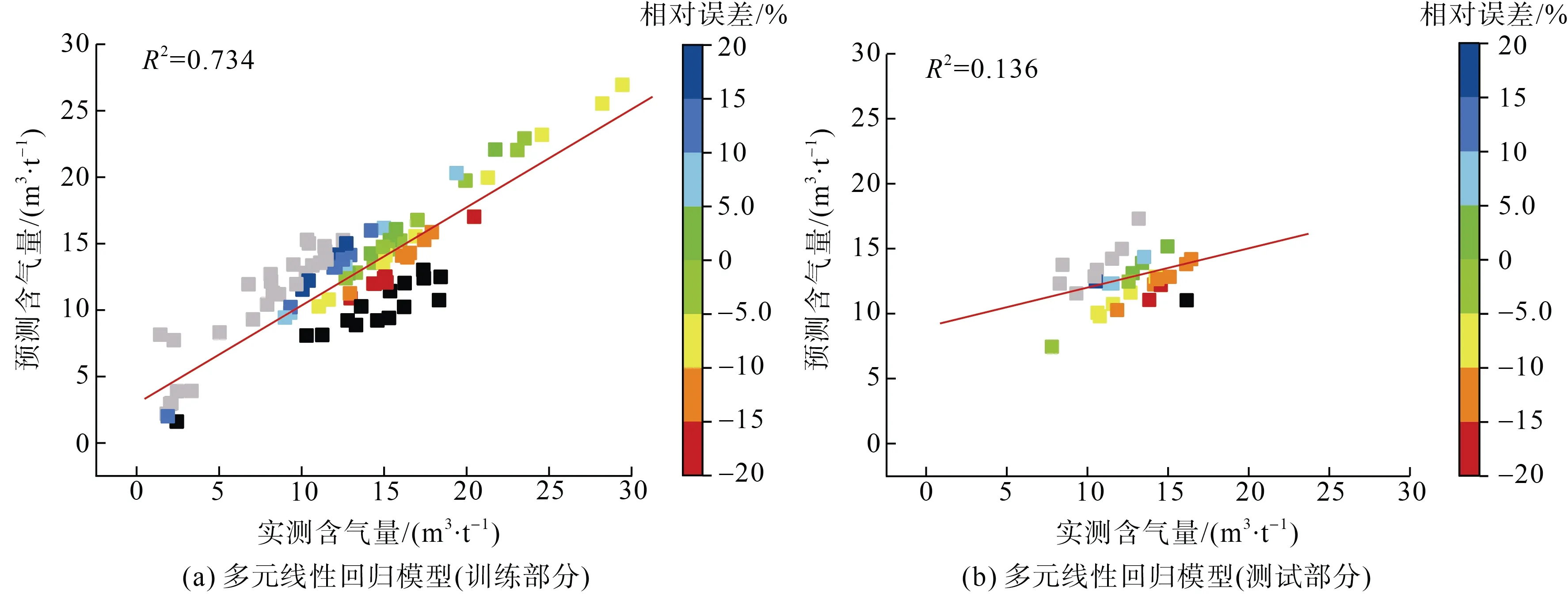
圖7 基于MIV 測井參數優選的多元線性回歸模型的預測結果與實測含氣量的交會圖Fig.7 The cross plot of prediction results and measured gas content

圖5、圖7 通過模型預測結果與實測結果的線性回歸下的擬合優度定性化判斷模型的預測效果，為進一步量化建模自變量優選及PSO 尋優給神經網絡建模帶來預測性能的改善情況，除擬合優度外，計算均方根誤差(RMSE)來對比模型預測效果，可以用來衡量模型預測結果與實測值的接近程度。均方根誤差是用來衡量模型預測值與真值之間的偏差，模型預測效果越好，均方根誤差值越小，其計算公式如下式：

式中：pti為模型預測數據；mti為實測數據；n為用于網絡訓練或測試的樣本數量。

據式(7)計算得到的模型評價指標 RMSE 結果(表5)，首先對比LSSVM 模型和PSO-LSSVM 模型的均方根誤差可知，在PSO 優化下，LSSVM 模型的預測精度有了顯著提高，預測結果的均方根誤差在訓練集和測試集分別達到了1.214 和1.226；再對比基于MIV 方法優選建模輸入自變量的LSSVM和PSO-LSSVM 模型，可知在MIV 優選的建模自變量下，二者的預測效果都有了很明顯的提升，基于MIV-PSO-LSSVM 模型的預測性能達到最佳，訓練集和測試集的預測均方根誤差分別為 1.025 和0.878；最后對比多元回歸模型和機器學習模型可知，多元線性回歸模型在數據不均衡時泛化能力極差。由圖7b 可知，基于線性回歸建模對測試集的預測效果不理想，說明線性回歸模型魯棒性和推廣應用性能較差，預測結果難以逼近真實值。綜合對比各模型的擬合優度和均方根誤差，可見MIV 方法的引入有效提升了本研究網絡建模的效果，模型的預測結果更為逼近真實值，有效的建模自變量組合可更好地通過LSSVM 模型擬合常規測井參數與煤層含氣量間隱含的函數映射關系，為煤層含氣量預測評價研究提供了新思路、新的建模策略。

表5 各煤層含氣量預測模型的預測精度評價指標Table 5 Evaluation indexes for prediction precision accuracy of each CBM content prediction model

4 結 論

a.經皮爾遜相關性分析常規測井參數與煤層含氣量及各測井參數彼此間的相關性可知各測井參數與含氣量間的相關程度差異較大，煤層含氣量測井響應特征明顯，各測井參數間存在不同程度的相關性。

b.簡單的線性分析不足以定量化反映測井參數與煤層含氣量間的真實函數映射關系，引入MIV 技術結合機器學習方法量化建模輸入自變量與輸出因變量間的影響程度，添加白噪聲自變量作為參照對比，根據計算的各參變量MIV 值，優選出優質的測井參數組合作為最終的網絡建模輸入，該策略可對測井參數進行有效的去冗余化處理，優化建模效果。

c.通過對比建立的 LSSVM、PSO-LSSVM、MIV-LSSVM、MIV-PSO-LSSVM 以及多元線性回歸模型預測性能，采用擬合優度和均方根誤差作為評價指標，結果表明：PSO 參數尋優下的LSSVM 模型預測精度有了明顯提升，MIV 優選測井參數可大幅提升模型的預測性能。基于機器學習算法建模效果遠勝于簡單的多元線性回歸模型，線性回歸模型的魯棒性及泛化能力極差，預測結果遠偏離真實值。

d.本研究針對煤層含氣量預測問題，圍繞煤層含氣量測井響應特征—測井參數優選—網絡建模參數尋優—模型建立及試算對比分析這一主線而提出的基于MIV 測井參數優選策略，對于采用機器學習煤層含氣量建模預測具有很好的效果，提出的MIV-PSO-LSSVM 模型為煤層含氣量預測提供了新方法，為滿足煤層氣勘探研究中的高精度要求提供了有力支撐。