四維黎曼時空下脈沖星導航模型精度分析
姜 宇,陳 曉,王龍奇,金 晶,馬家辰
(1.哈爾濱工業大學 航天學院,黑龍江 哈爾濱 150001;2.上海衛星工程研究所,上海 201109)
0 引言
脈沖星是一種高速自轉的強磁化中子星,具有自轉周期穩定、輻射光子能量集中的特點。它能夠為近地軌道、深空和星際空間飛行的航天器提供位置、速度、時間和姿態等導航信息,實現對長時間在軌航天器的高精度自主導航與控制,具有廣闊的工程應用前景[1-2]。
脈沖星的自轉軸與磁軸存在固定夾角,又因為脈沖星的自轉周期非常穩定,航天器接收到周期性的光子信號。
記錄航天器單位時間內接收的光子數可以獲得脈沖星觀測輪廓,對比脈沖星的觀測輪廓和太陽系質心(Solar System Barycenter,SSB)的標準輪廓可以得到光子到達航天器與SSB 的時間差。把時間差作為觀測量建立三維觀測模型,結合軌道動力學模型,利用相關濾波算法可以得到航天器的位置和速度信息[3-7]。
隨著空間探測向大尺度時空發展,計時精度向納秒量級提高,三維歐式空間下的脈沖星光子傳播模型已經不能滿足精度要求。光子在傳播過程中,不僅需要考慮其周年視差效應、多普勒頻移以及等離子體的色散延緩,還要考慮太陽系引力的彎曲效應[8-10]。
文獻[11]基于DSX 體系下的后牛頓近似方法,將SSB 坐標系作為航天器導航的參考系,推導了1PN、2PN 度規下的高精度觀測模型,可以滿足納秒量級的時間測量精度。
文獻[12-13]提出在四維光坐標框架下討論脈沖星光子傳播問題,將4 個脈沖星的固有時作為四維平直時空的光坐標,可以為太陽系內的任意觀測者導航,由此建立相對論定位系統理論框架。
文獻[14]在四維黎曼時空中引入相對論定位系統,建立四維觀測模型,與傳統的三維觀測模型相比引入時間狀態量,提高了時間估計的準確性,且不必推算標準輪廓的相位,減小了標準輪廓的擬合誤差。
X 射線脈沖星自主導航依賴于精確的時間測量,航天器時鐘記錄的固有時與SSB 坐標系下的坐標時不同步,在500 s 的觀測窗口下,固有時和坐標時會產生微妙量級的誤差,代入迭代過程會導致濾波器發散,所以需要引入時間轉換模型。利用光子運動的四維時空間隔為零,可以得到固有時與坐標時的基本關系。
文獻[15-16]研究環火星探測器星載時鐘在1PN 度規下的時間轉換關系,通過數值分析得出時間不同步主要受太陽引力和航天器速度影響,可達亞秒/年量級。上述關系式以坐標時作為自變量進行積分運算,并且積分式中涉及航天器的位置、速度信息,很難實現從固有時到坐標時的轉換。
文獻[17]根據廣義相對論的后牛頓近似理論,在忽略太陽系天體自轉和扁率的情況下,利用能量守恒定律推導出航天器繞飛的時間轉換模型,模型精度在納秒量級。文獻[18]針對航天器繞地變軌時可能做拋物線或雙曲線運動推導了更加全面的時間轉換模型,對文獻[19]進行了補充分析。
本文基于繞飛軌道研究高精度脈沖星導航模型,為脈沖星導航的深空探測提供理論基礎,所做工作集中在以下兩方面:在四維黎曼時空下建立脈沖星導航系統狀態模型和四維觀測模型,并基于無跡卡爾曼濾波(UKF)方法設計脈沖星導航算法;對引入的四維觀測模型和時間轉換模型進行誤差分析,研究影響導航精度的主要因素。
1 四維黎曼時空下的X 射線脈沖星導航模型
1.1 航天器軌道力學模型
選取太陽系質心天球參考系(Barycentric Celestial Reference System,BCRS)的時空度規,建立帶有時間轉換項的航天器軌道運動學模型。X 射線脈沖星導航原理圖如圖1 所示。

圖1 X 射線脈沖星導航原理圖Fig.1 Schematic diagram of X ray pulsar-based navigation
四維黎曼時空下航天器的狀態x定義為

式中:t為航天器的坐標時;rsa=rse+rea、vsa=vse+vea分別為航天器相對于SSB 的位置和速度矢量;rse、vse分別為繞飛行星相對于SSB 的位置和速度矢量 ;rea=[rea,x rea,y rea,z]T、vea=[vea,x vea,y vea,z]T分別為航天器相對于行星的位置和速度矢量。
相對繞飛行星建立航天器軌道運動學方程為[5]
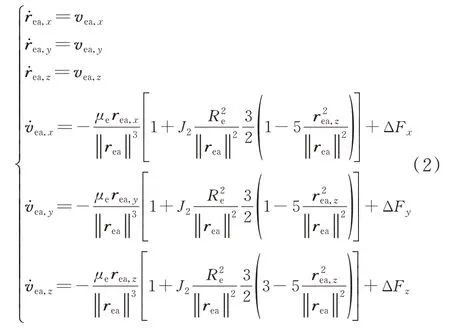
式中:Re為繞飛行星的半徑;μe為繞飛行星的引力常數;J2為攝動項系數;ΔF=[ΔFx,ΔFy,ΔFz]T為攝動項矩陣,指的是包括月球引力攝動、潮汐攝動在內的其他攝動力影響。將式(2)簡寫為

在四維黎曼時空下,航天器的坐標時可由時鐘記錄的固有時轉換得到。在1PN 度規下,忽略星體的自轉、扁率以及太陽與SSB 間距,可得到從航天器固有時至SSB 滿足納秒量級精度的時間轉換模型[16]:

式中:Δτ為星載時鐘走過的固有時;Δt為Δτ時間內時鐘經歷的坐標時;c為光速;等號后的第1 項為Δt時間內運動產生的綜合時延;為引力修正因子;μs為太陽引力常數;μe為行星的引力常數;ase為行星繞太陽作橢圓運動的長半軸;aea為航天器繞行星運動的長半軸。
將式(4)簡寫為

式中:Δt0=LΔτ包含了行星引力產生的頻移,稱為引力時延;包含了航天器運動以及行星繞太陽運動偏離圓軌道所產生的頻移,稱為偏軌時延;包含了航天器軌道曲率變化所產生的頻移,稱為航天器曲率時延;包含了行星軌道曲率變化所產生的頻移,稱為行星曲率時延;Δt0為長期影響項;Δt1、Δt2、Δt3為周期影響項。
根據式(1)~式(4),航天器的狀態模型最終描述為

式中:f(x,τ)=;τ為星載時鐘的固有時刻,這是實際飛行任務中可獲取的時間狀態量;w(τ)為系統的傳遞噪聲矩陣。
1.2 四維觀測模型
通常意義下的時間概念是太陽系質心坐標系下的航天器坐標時,而實際中可獲取的時間變量是星載時鐘原子時,它們之間存在一種轉換關系。在高精度要求的情況下,坐標時成為了一個關于航天器狀態和原子時變化的新觀測量,同時單顆脈沖星僅可以在組合導航中應用,或者作投影方向上的導航算法精度驗證,不能實現自主導航。因此,需要引入四維觀測模型。
根據相對論定位系統的基本思想和后牛頓引力理論,將脈沖星P(P=1,2,3,4)走過的固有時TP作為直接觀測量[13],建立四維觀測模型如下:

根據式(7)和式(8),脈沖星導航的四維觀測模型簡寫為

四維觀測模型相比傳統的三維觀測模型,引入了時間狀態量,且不必推算標準輪廓的相位,具有更精確的時間估計,更小的相位擬合誤差。
2 基于UKF 的脈沖星導航算法
根據式(6)和式(9)得到脈沖星導航系統的離散模型為

式中:wk、vk的協方差矩陣分別為Qk和Rk,且滿足
利用UKF 算法進行脈沖星導航濾波的步驟如下:
步驟1時間轉換。上一時刻到當前時刻走過的固有時為Δτk?1,根據式(4)可將航天器記錄的固有時轉換為坐標時,即

步驟2構造采樣點。卡爾曼濾波傳遞狀態量的一階矩和二階矩信息,對于狀態均值及其協方差矩陣Pk?1,選取比例對稱采樣策略對其進行采樣,但在采樣前需要保證算法的穩定性。由于協方差矩陣Pk?1存在時間項的極小對角值,在迭代過程中不能保證其對稱半正定,需對Pk?1作對稱正定化處理:


式中:α為比例縮放因子,可通過調整α取值來調節采樣點與中心點的距離;β為函數f(?)的高階項參數;κ涉及高 階矩的選取,一般 取為0 或3?n,但應確保協方差矩陣傳遞的半正定性。

式中:(·)i算子為取矩陣的第i列信息。
將采樣點展開為

步驟3預測。利用狀態模型對每個采樣點進行預測,得到

計算狀態均值及其協方差矩陣為

計算觀測量及其均值為

步驟4更新。觀測量與狀態量之間的預測協方差陣分別為

濾波器增益為

更新時刻的狀態均值及其協方差矩陣為

3 仿真分析
3.1 仿真條件
仿真采用DE405 星歷,初始時間為1990 年7 月7 日12 時0 分0 秒,時長為35 d,觀測時間間隔為500 s。
本文的導航模型適用于太陽系任一行星的繞飛軌道,這里以繞飛地球高軌為例,其軌道參數見表1。

表1 軌道參數Tab.1 Orbit parameters
選用Arecibo 天文臺長期觀測的4 顆毫秒級脈沖星,其參數見表2。

表2 脈沖星參數Tab.2 Pulsar parameters
計算機仿真環境為CPU 4 核2.5 GHz,內存8 GB,Matlab 2012b。初始狀態誤差δx0、初始協方差陣P0、系統噪聲協方差陣Qk、觀測噪聲協方差陣Rk設置如下:

3.2 仿真結果
UKF 濾波后的導航結果如圖2所示,導航的位置誤差穩定在10 m 量級,時間誤差穩定在nm 量級,速度誤差穩定在0.01 m/s 量級。下面分別討論時間轉換模型和四維觀測模型中的時延項對導航精度的影響。

圖2 四維黎曼時空下脈沖星導航模型的估計誤差Fig.2 Estimation errors of the pulsar-based navigation model in 4D Riemann space-time
3.2.1 時間轉換模型精度分析
時間轉換模型的各個時延項在迭代中所占的比重如圖3 所示。其中,引力時延Δt0數值最大,達10?5s 量級;偏軌時延Δt1、行星曲率時延Δt3比重相對較小,為10?7s 量級;航天器曲率時延Δt2數值最小,為10?10s 量級。忽略時間轉換模型中的任一時延項進行導航,結果如圖4 所示。可以看出,忽略Δt0對導航精度的影響最大,達105m 量級;忽略Δt1、Δt3對導航精度的影響相對較小,為103m 量級;忽略Δt2對導航精度的影響最小,為10 m 量級。這表明在時間轉換過程中,引力時延、航天器偏軌時延以及繞飛行星曲率時延等因素對導航精度的影響較大,航天器繞行星飛行的曲率變化對導航精度的影響較小。上述分析驗證了引入時間轉換模型的必要性。

圖3 時間轉換模型中的時延項比重Fig.3 Proportion of delay items in the time transformation model

圖4 忽略時間轉換模型時延項的導航定位誤差Fig.4 Positioning errors without a time transformation term
3.2.2 四維觀測模型精度分析
四維觀測模型中的各個時延項在迭代中所占比重如圖5 所示。圖5 中,引力時延ρ3(r)數值較大,達10?4s 量級,周年視差時延ρ1(r)數值較小,達10?7s量級,脈沖星自行時延ρ2(r)總體上呈增長趨勢,在仿真時間內與ρ1(r)達到同一量級。若忽略其中一項進行導航,結果如圖6 所示。

圖6 忽略四維觀測模型時延項的導航定位誤差Fig.6 Positioning errors without a time delay term of the 4D observation model
可以看出,忽略ρ3(r)對導航精度的影響很大,達104m 量級;忽略ρ1(r)、ρ2(r)對導航精度的影響較小,為103m級,并且由于脈沖星自行時延有累積增長趨勢;忽略ρ2(r)引起的誤差按其趨勢增長,與圖5的結果吻合。上述分析表明,在量測過程中太陽系的引力遠大于周年視差效應、脈沖星自行對導航精度的影響。

圖5 四維觀測模型中時延項比重Fig.5 Proportions of delay items in the 4D observation model
4 結束語
本文建立的導航模型考慮了廣義相對論的影響,通過引入時間轉換模型可適應ns 量級的計時精度,在此基礎上分析了導航模型的精度影響因素,為深空探測的工程應用提供了理論參考。同時使用本文建立的導航模型可以簡化脈沖星信號處理過程,為脈沖星導航算法提供更精準的模型基礎。

