基于特征模型的力矩受限衛(wèi)星姿態(tài)抗飽和設(shè)計
郭瑞科,胡 軍,李毛毛,張 濤
(北京控制工程研究所,北京 100190)
0 引言
航天器技術(shù)的發(fā)展和航天任務(wù)復(fù)雜度的提高對控制能力提出了更高的要求,然而航天器姿態(tài)控制中執(zhí)行器所能輸出的控制力矩存在一定限制,也就是存在飽和非線性。如果設(shè)計控制器不考慮執(zhí)行器存在飽和非線性,當(dāng)執(zhí)行器發(fā)生飽和時,控制器的輸出和被控對象的輸入值不相等,可能會導(dǎo)致航天器姿態(tài)控制精度變差或閉環(huán)系統(tǒng)不穩(wěn)定。通過設(shè)計抗飽和補(bǔ)償器恢復(fù)閉環(huán)系統(tǒng)性能或者穩(wěn)定性,是解決執(zhí)行器飽和影響控制性能或閉環(huán)系統(tǒng)穩(wěn)定性的一種途徑[1]。
目前,航天器姿態(tài)控制抗飽和研究取得一些進(jìn)展[2-8]。MARCO 等[9]提出了基于線性矩陣不等式(LMI)的線性離散系統(tǒng)抗飽和設(shè)計方法,給出了靜態(tài)和動態(tài)抗飽和補(bǔ)償器的構(gòu)造算法,尤其是對于靜態(tài)或者被控對象同階的抗飽和補(bǔ)償器構(gòu)造條件可以轉(zhuǎn)化為凸約束的LMI 條件。于海祥等[10]針對大角度姿態(tài)機(jī)動衛(wèi)星存在控制輸入飽和問題,在建立被控對象特征模型的基礎(chǔ)上,設(shè)計了基于特征模型的低增益反饋控制器,使得復(fù)雜被控對象也可以用低增益的設(shè)計方法解決控制輸入飽和問題。王明釗等[11]將LQG 控制方法和基于LMI 抗飽和補(bǔ)償器相結(jié)合,保證了控制輸入受限航天器閉環(huán)穩(wěn)定,且滿足最優(yōu)的L2 指標(biāo)。李德婷等[12]針對單框架控制力矩陀螺的力矩輸出具有奇異飽和性能的特點,設(shè)計了基于平坦微分理論的快速參考軌跡規(guī)劃方法和滑模控制器相結(jié)合的控制方法,避免出現(xiàn)奇異飽和失效現(xiàn)象。文獻(xiàn)[13]考慮了一類具有狀態(tài)獨立的輸入飽和非線性系統(tǒng),提出了新的控制策略,設(shè)計的非線性控制器使得系統(tǒng)是局部漸近穩(wěn)定的。WADA 等[14]對使用模型預(yù)測控制器的線性離散系統(tǒng)設(shè)計抗飽和補(bǔ)償器,將抗飽和補(bǔ)償器的求解轉(zhuǎn)化為LMI 優(yōu)化問題,保證了存在輸入飽和時的系統(tǒng)穩(wěn)定性并改善了瞬態(tài)響應(yīng)。然而這些方法都只適用于定常線性離散系統(tǒng),對于非線性系統(tǒng)或者系統(tǒng)參數(shù)不確定時,該方法應(yīng)用受到限制。
吳宏鑫等[15]提出了根據(jù)對象動力學(xué)特性、環(huán)境特征和控制性能要求相結(jié)合來建模的特征建模思想,以期在滿足性能指標(biāo)的情況下設(shè)計出簡單低階控制器。一般情況下,特征模型用慢時變低階差分方程描述,工程和應(yīng)用研究中使用最廣泛的是二階差分特征模型。基于特征建模的黃金分割控制能保證參數(shù)未知定常系統(tǒng)在過渡階段,參數(shù)估計未收斂情況下閉環(huán)穩(wěn)定,設(shè)計簡單,參數(shù)魯棒性好。但基于特征模型的黃金分割控制器所針對的對象模型還沒有考慮過執(zhí)行器存在飽和的情況。當(dāng)不考慮執(zhí)行器飽和現(xiàn)象,常規(guī)設(shè)計的控制器在執(zhí)行器發(fā)生飽和時將不能保證控制性能或者閉環(huán)系統(tǒng)的穩(wěn)定性。
本文提出將黃金分割控制器和基于LMI 抗飽和設(shè)計相結(jié)合的控制方法,針對存在控制力矩飽和約束的衛(wèi)星姿態(tài)跟蹤控制問題,首先設(shè)計不考慮輸入飽和的定常黃金分割控制器;其次用特征模型取代原被控對象求解抗飽和補(bǔ)償器,將求解抗飽和補(bǔ)償器的約束條件轉(zhuǎn)化為凸約束的LMI 條件,設(shè)計過程保證了整個閉環(huán)系統(tǒng)的穩(wěn)定性。數(shù)值仿真驗證了所提出方法對控制力矩受限衛(wèi)星姿態(tài)跟蹤控制的有效性和魯棒性。
1 問題描述
1.1 撓性衛(wèi)星動力學(xué)系統(tǒng)描述
撓性衛(wèi)星俯仰軸動力學(xué)的簡化模型可以寫成如下形式:
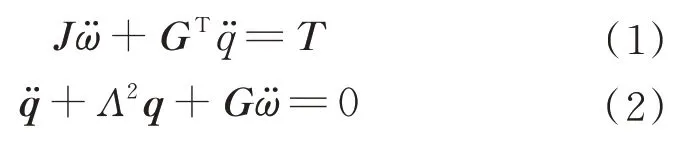
式中:J為衛(wèi)星轉(zhuǎn)動慣量;ω為俯仰角速度;T為控制力矩;G=[g1g2]T為撓性模態(tài)與衛(wèi)星俯仰運動的耦合系數(shù)矩陣;q=[q1q2]T為模態(tài)坐標(biāo);Λ=diag(Λ1Λ2)為約束模態(tài)頻率。
參考文獻(xiàn)[10],上述撓性衛(wèi)星俯仰軸動力學(xué)模型的特征模型可以用如下形式的二階差分方程表示:
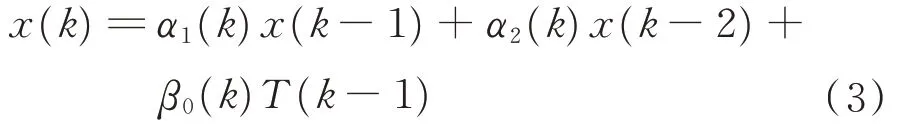
式中:α1(k)、α2(k)、β0(k) 未知,但在已知閉凸集之內(nèi)[15]。
參考文獻(xiàn)[15]中定理5.1,對式(3)中α1(k)、α2(k)、β0(k)取穩(wěn)態(tài)值,得到
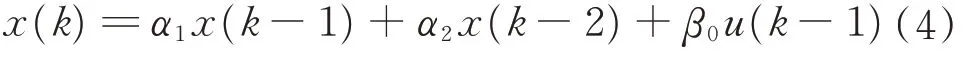
對式(4)設(shè)計定常黃金分割控制器,作為系統(tǒng)控制輸入未受限時的標(biāo)稱控制器,可以保證閉環(huán)系統(tǒng)穩(wěn)定并滿足性能,即
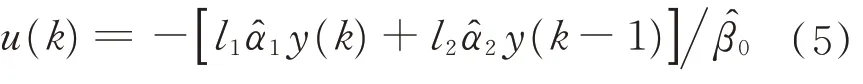
式中:l1=0.382;l2=0.618;為特征模型辨識參數(shù),此處取穩(wěn)態(tài)值。
當(dāng)被控對象的控制輸入存在飽和非線性時,也就是控制輸入滿足
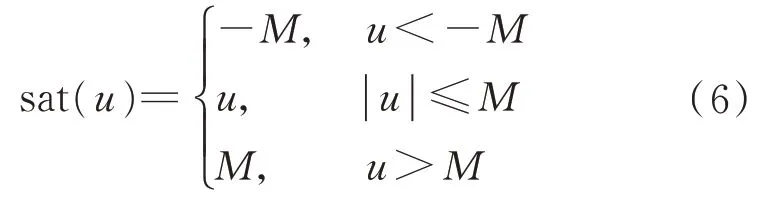
需要設(shè)計線性抗飽和補(bǔ)償器,保證參考輸入w和輸出性能z之間l2增益滿足控制要求。假設(shè)設(shè)計naw階的抗飽和補(bǔ)償器,naw≥0,定 義q=u?sat(u),
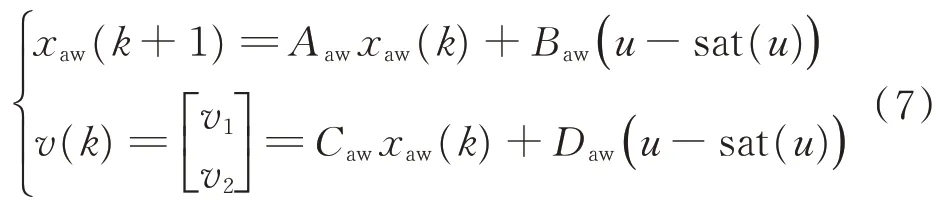
由被控對象、黃金分割控制器、抗飽和補(bǔ)償器組成的閉環(huán)系統(tǒng)示意圖如圖1 所示。
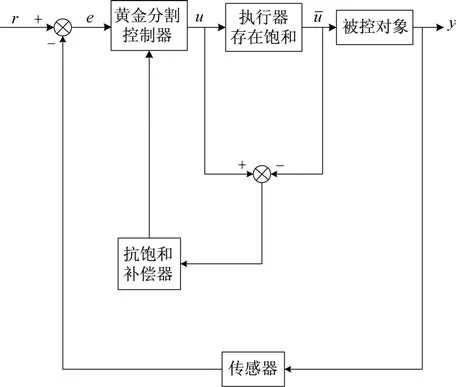
圖1 抗飽和閉環(huán)系統(tǒng)Fig.1 Anti?windup closed?loop system
1.2 控制律變換
為了便于設(shè)計抗飽和補(bǔ)償器,需要將定常黃金分割控制律寫成狀態(tài)空間形式。基于誤差的黃金分割控制律為

若被控對象存在控制輸入飽和,加入抗飽和補(bǔ)償器輸出的控制律為
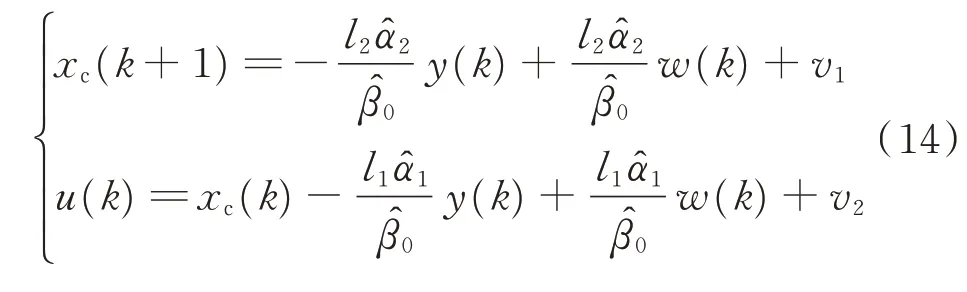
1.3 閉環(huán)系統(tǒng)
為便于求解抗飽和補(bǔ)償器,將式(4)寫成狀態(tài)空間形式,得

2 抗飽和補(bǔ)償器構(gòu)造
2.1 抗飽和補(bǔ)償器存在性線性矩陣不等式條件
定理1給定被控對象(15)、控制器(13),當(dāng)且僅當(dāng)存在正定對稱的矩陣R11、S,矩陣Z,正數(shù)γ,使得下述線性矩陣不等式可行時,被控對象(15)、控制器(13)組成的閉環(huán)系統(tǒng)在控制輸入滿足式(7)飽和非線性約束時,使閉環(huán)系統(tǒng)適定且保證局部二次型l2性能的抗飽和補(bǔ)償器(7)存在[8]。
下文中對矩陣X,He(X)=X+XT,
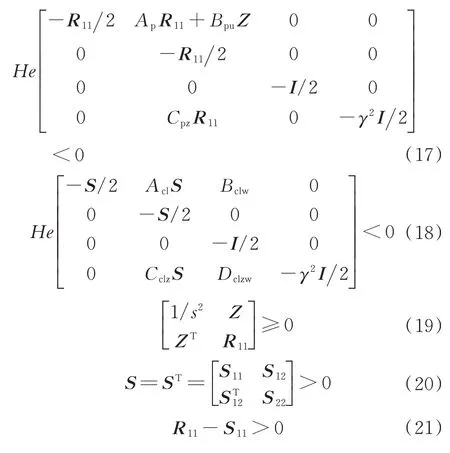
2.2 抗飽和補(bǔ)償器的構(gòu)造方法
前述定理給出了與被控對象同階的抗飽和補(bǔ)償器可行性線性矩陣不等式條件。然而在抗飽和設(shè)計中,需要求解出抗飽和補(bǔ)償器的系數(shù)矩陣,因而下面給出具體的構(gòu)造方法[16]:


3 實驗仿真
考慮文獻(xiàn)[10]中的對象,對稱撓性帆板衛(wèi)星的俯仰軸動力學(xué),采樣時間Ts=0.1 s,模型參數(shù)如下:

控制輸入u限制為±30,可以設(shè)計被控對象同階的抗飽和補(bǔ)償器,通過固定參考輸入yr的l2增益s,求得最優(yōu)γ,以實現(xiàn)閉環(huán)穩(wěn)定和局部的性能指標(biāo)。
抗飽和補(bǔ)償器與被控對象同階(naw=2),取s=0.29,可求得γ=349.06,抗飽和補(bǔ)償器系數(shù)矩陣為

控制輸入未受限時,所設(shè)計的控制律可以很好地跟蹤參考輸入,控制量最大值為978.9。當(dāng)控制輸入的幅值限值在±30 時,閉環(huán)系統(tǒng)受到飽和影響,可以看到控制性能明顯變差,輸出難以跟蹤參考輸入,控制輸入在±30 多次振蕩,如圖2 和圖3所示。
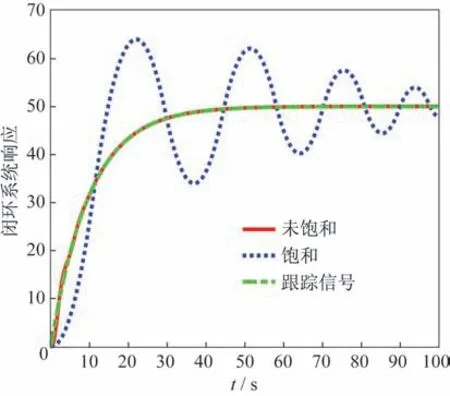
圖2 不存在與存在輸入飽和時的閉環(huán)響應(yīng)Fig.2 Closed-loop responses without and with input saturation
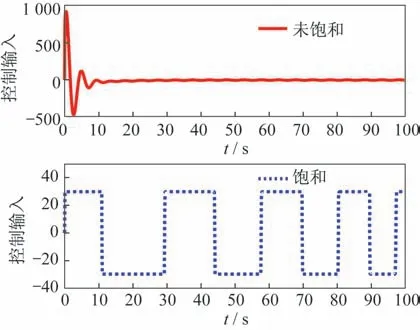
圖3 不存在與存在輸入飽和時的控制量Fig.3 Control inputs without and with input saturation
3.1 被控對象同階抗飽和補(bǔ)償器(naw=np=2)
根據(jù)2.2 節(jié)步驟設(shè)計的被控對象同階抗飽和補(bǔ)償器控制結(jié)果如圖4 所示。圖中可見,采用被控對象同階抗飽和補(bǔ)償器之后,閉環(huán)系統(tǒng)的輸出能較好地跟蹤參考輸入,相比較與飽和系統(tǒng)控制效果有明顯提升。通過圖5 所示的幾拍bang-bang 控制能夠很快地恢復(fù)不受限的閉環(huán)響應(yīng),說明這種動態(tài)抗飽和補(bǔ)償器是有效的。需要注意的是,在初始跟蹤階段,跟蹤性能還是有較小的損失,這也是抗飽和補(bǔ)償器在保證飽和性能同時,不可避免地?fù)p失小信號時的閉環(huán)響應(yīng)性能。
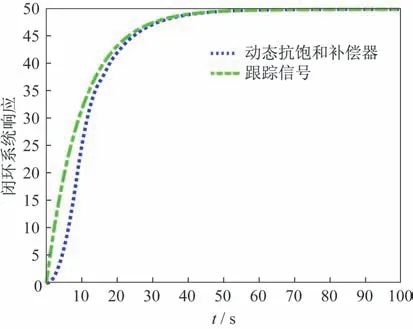
圖4 采用動態(tài)抗飽和補(bǔ)償器的閉環(huán)響應(yīng)Fig.4 Closed-loop responses with dynamic anti-windup compensator
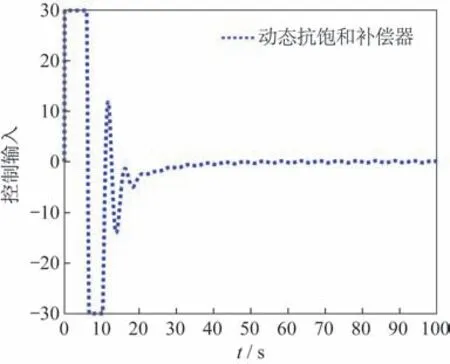
圖5 采用動態(tài)抗飽和補(bǔ)償器時的控制量Fig.5 Control input with dynamic anti-windup compensator
3.2 黃金分割控制器與低增益飽和控制器對比仿真
此處進(jìn)一步對比了定常黃金分割控制律和文獻(xiàn)[10]中所采用低增益控制律時,閉環(huán)系統(tǒng)響應(yīng)和控制量的不同。如圖6 所示,控制輸入受限時,采用兩種控制器的閉環(huán)系統(tǒng)都在瞬態(tài)響應(yīng)有輕微的性能損失,但采用動態(tài)抗飽和補(bǔ)償器的黃金分割控制相比低增益飽和控制器能更好地跟蹤參考信號,同時采用定常黃金分割控制的控制量只有較少的振蕩,變化較平滑,如圖7 所示。

圖6 采用動態(tài)抗飽和補(bǔ)償器和低增益控制器的閉環(huán)響應(yīng)Fig.6 Closed-loop responses with dynamic anti-windup compensator and low-gain controller
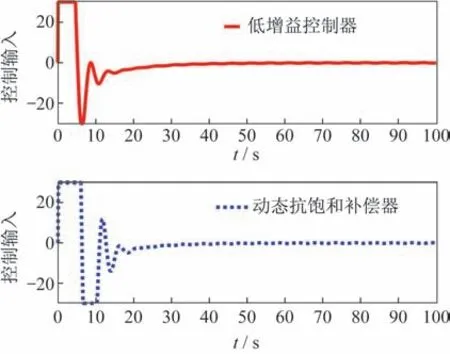
圖7 采用動態(tài)抗飽和補(bǔ)償器和低增益控制器的控制量Fig.7 Control input with dynamic anti-windup compensator and low-gain controller
4 結(jié)束語
本文將黃金分割控制器和基于LMI 抗飽和設(shè)計相結(jié)合,首先設(shè)計不考慮輸入飽和的定常黃金分割控制器;其次用特征模型取代原被控對象來求解抗飽和補(bǔ)償器,將求解抗飽和補(bǔ)償器的約束條件轉(zhuǎn)化為凸約束的LMI 條件。設(shè)計過程保證了整個閉環(huán)系統(tǒng)的穩(wěn)定性,解決了存在控制力矩飽和約束的衛(wèi)星姿態(tài)跟蹤控制問題。數(shù)值仿真驗證了所提出方法對控制力矩受限衛(wèi)星姿態(tài)跟蹤控制的有效性和魯棒性。

