單軸轉向架跨座式單軌車輛的主動控制研究
辛 亮,杜子學,楊 震,許舟洲
(1.重慶交通大學 軌道交通研究院,重慶 400074;2.重慶交通大學 機電與車輛工程學院,重慶 400074)
0 引 言
跨座式單軌車輛作為一種獨特的城市軌道交通制式,有別于地鐵車輛,具有廣闊的應用前景[1]。目前,跨座式單軌車輛類型主要有雙軸轉向架跨座式單軌車輛(以下簡稱雙軸單軌車輛)和單軸轉向架跨座式單軌車輛(以下簡稱單軸單軌車輛)兩種類型[2]。相比于雙軸單軌車輛,單軸單軌車輛具有輕量化、低地板、造價低和維護方便等優點,是一種適用于中小運量的城市軌道交通新型制式[3]。
單軌車輛騎跨在軌道梁上,不僅走行輪與軌道梁頂部接觸,分布在轉向架兩側的導向輪和穩定輪也分別與軌道梁側面接觸。單軌車輛運行時,軌道梁路面不平度通過輪胎和轉向架傳遞給車體,引起車輛振動,從而影響單軌車輛運行品質。K.GODA等[4]考慮軌道不平度對輪胎的作用力,建立了9自由度單軌車輛動力學模型,并進行了頻譜分析;C.H.LEE等[5]以大阪跨座式單軌車輛及鋼橋為研究對象,建立了車橋耦合動力學模型,并從耦合動力學角度分析了車橋耦合系統中的相互作用關系,同時進行了“單軌車輛-鋼橋”系統實地測試,驗證了其模型分析所得結果正確性;趙樹恩等[6]考慮輪胎非線性特性的單軌車輛動力學模型,并分析了車速和曲率半徑對振動響應影響;李軍等[7]采取數值仿真方法,分析了不同車速、風速、合成風向角的單軌車輛在橫風作用時動力響應;杜子學等[8-10]分析了走行輪、穩定輪、空氣彈簧失效等工況對單軌車輛動力學響應影響。上述學者分析了不同工況下單軌車輛動力學響應;但如何主動抑制單軌車輛振動,提高單軌車輛運行品質卻鮮有報道。傳統汽車中常采用主動懸架技術來提高車輛運行品質[11],并采用了很多控制算法,如天棚控制[12]、PID控制[13]、模糊控制[14]和神經網絡控制[15]等,均能達到不錯的控制效果。
因此,筆者以單軸單軌車輛為研究對象,建立了15自由度單軸單軌車輛主動控制動力學模型;以日本軌道譜為路面輸入,基于ANFIS-PID控制算法,進行單軌車輛橫向和垂向運動控制,以期為單軸單軌車輛主動控制研究提供思路。
1 車輛主動控制動力學模型
1.1 車輛建模
所謂單軸單軌車輛,即是其每個轉向架只有一對走行輪,是一種新型的單軌制式,如圖1。單軸單軌車輛包括一個車體和兩個轉向架,每個轉向架有2個走行輪、4個導向輪和2個穩定輪。車體與前、后轉向架之間通過沙漏簧、垂向和橫向油壓減振器及橫向止擋組成的中央懸掛系統分別在垂向、橫向和縱向連接。

圖1 單軸轉向架結構
圖2給出了某型單軸單軌車輛拓撲構型。為抑制車體振動,提高車輛運行品質,在車輛和每個轉向架間布置了4個(2個橫向和2個垂向)作動器,兩個轉向架共8個作動器。
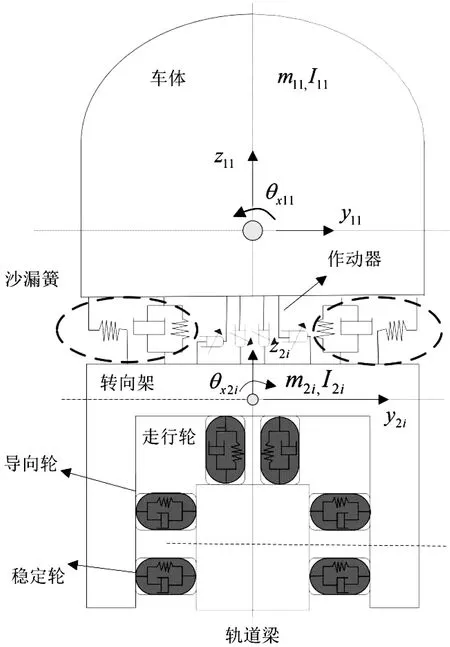
圖2 單軸單軌車輛的拓撲構型
考慮單軸單軌車輛安裝空間,筆者將橫向作動器和橫向油壓減振器并聯,垂向作動器和垂向油壓減振器并聯,如圖3。車輛作動器主要由伺服放大器、伺服閥和液壓缸組成。其工作原理為:傳感器測量單軌車輛加速度信號,反饋給控制器,經控制器計算,得到電壓信號,伺服放大器再將電壓信號轉化為電流信號輸入給伺服閥,控制伺服閥的閥門開度,從而控制液壓油流量和壓力,進而控制液壓缸輸出力,達到抑制單軌車輛振動目的。

圖3 單軸單軌車輛作動器的布置
考慮車體和前、后轉向架的橫向、垂向、側傾、俯仰和橫擺運動,共15個自由度。則根據拉格朗日方程,車輛動力學方程[16]可描述如式(1):
(1)
式中:T為動能;Ue為彈性勢能;Uq為阻尼耗能;Qj為廣義力和力矩;qj為廣義坐標;(·)為對時間求導。
動能、彈性勢能、阻尼勢能和廣義力和力矩可表示如式(2)~(5):
(2)
(3)
(4)
(5)
式中:m11,m21,m22分別為車體、前轉向架和后轉向架質量;y11,y21,y22分別為車體、前轉向架和后轉向架橫向位移;z11,z21,z22分別為車體、前轉向架和后轉向架垂向位移;θx11,θx21,θx22分別為車體、前轉向架和后轉向架側傾角;θy11,θy21,θy22分別為車體、前轉向架和后轉向架俯仰角;θz11,θz21,θz22分別為車體、前轉向架和后轉向架橫擺角;Ki1jn和Ci1jn分別為沙漏簧的垂向剛度和阻尼;Ki2jn和Ci2jn分別為走行輪剛度和阻尼;Ki3jn和Ci3jn分別為導向輪剛度和阻尼;Ki4jn和Ci4jn分別為穩定輪剛度和阻尼;Ki5jn和Ci5jn分別為沙漏簧的橫向剛度和阻尼;下標i為車輛轉向架位置(i=1, 2代表前、后轉向架),j為轉向架中的車輪位置(j=1, 2代表前輪、后輪),n為車輛左右兩側位置(n=1, 2代表左側、右側);Rimjn為相對位移;δ1j為Kronecker常數;fyj和fzj分別為橫向和垂向主動力。
1.2 軌道梁路面不平度分析
不同等級路面區別主要在于路面粗糙度的不同,一般路面不平度由Gq表示。根據文獻[17],可將路面功率譜密度表示如式(6):
(6)
式中:Ω為空間頻率;α,β,n分別為路面粗糙度系數。
參照文獻[18]數據,通過功率譜擬合得到α,β,n的取值如表1。

表1 功率譜取值
2 ANFIS-PID控制算法
PID控制器根據受控對象給定值與實際輸出值偏差比例、積分和微分,通過線性組合決定控制器輸出量大小。PID控制規律如式(7):
(7)
式中:u(t)為PID控制器輸出;kp,ki,kd分別為比例系數、微分系數和積分系數;e(t)為給定值與實際輸出值的偏差,e(t)=yd(t)-y(t)。
PID控制器結構簡單,可靠性好,但依賴于精確的數學模型,對復雜系統難以達到預期的控制效果。而模糊控制和神經網絡控制都是處理復雜系統的有力工具[19]。故筆者在傳統PID控制基礎上,結合模糊控制和神經網絡控制,設計了ANFIS-PID控制器,從而達到了對復雜系統良好控制性能的效果。ANFIS-PID控制輸入為車身和車身速度變化率,輸出為作動器主動力。
ANFIS-PID控制器主要包括ANFIS和PID兩部分,如圖4。ANFIS為多輸入單輸出系統,而PID控制器kp,ki,kd均需要在線調整,故設計了3個ANFIS控制器,如式(8)~(10):
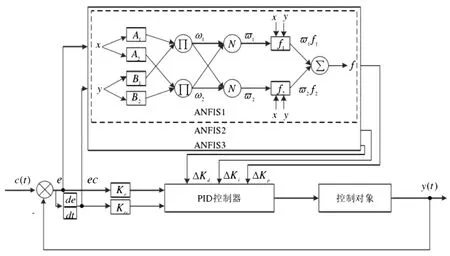
圖4 ANFIS-PID控制器
kp=kp0+Δkp
(8)
ki=ki0+Δki
(9)
kd=kd0+Δkd
(10)
式中:kp0,ki0,kd0分別為PID控制器初始參數;Δkp, Δki, Δkd分別為3個ANFIS控制器輸出,從而自適應改變PID系統的例系數、微分系數和積分系數。
3 分析與討論
假設單軌車輛在直線上行駛,筆者分別對原始單軌車輛、PID控制單軌車輛和ANFIS-PID控制單軌車輛進行仿真。車速設定為70 km/h,采用Runge-Kutta法進行時間推進,設置仿真時間步長為0.005 s,仿真總時間為10 s。
將車身橫向和垂向加速度作為評價指標,其仿真結果對比如圖5。圖5中:實線為原始單軌車輛結果,虛線為PID控制單軌車輛結果,點劃線為ANFIS-PID控制單軌車輛結果。從圖5可看出:相比于原始單軌車輛,PID控制和ANFIS-PID控制單軌車輛的橫向和垂向加速度均有一定程度減小,表明所設計的單軌單軸轉向架主動控制系統均能抑制車輛振動,提高車輛運行品質。
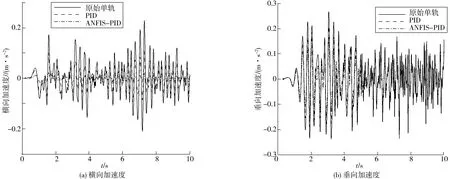
圖5 原始單軌、PID控制單軌和ANFIS-PID控制單軌加速度曲線
為更清晰對比主動控制效果,表2、3分別給出了仿真結果的均方根值和峰值對比。由表2、3可知:相比于原始結構,PID控制和ANFIS-PID控制的橫向加速度均方根值分別降低了48.37%和89.06%,垂向加速度均方根值分別降低了19.41%和34.32%;橫向加速度峰值分別降低了53.00%和90.30%,橫向加速度峰值分別降低了21.72%和37.60%。
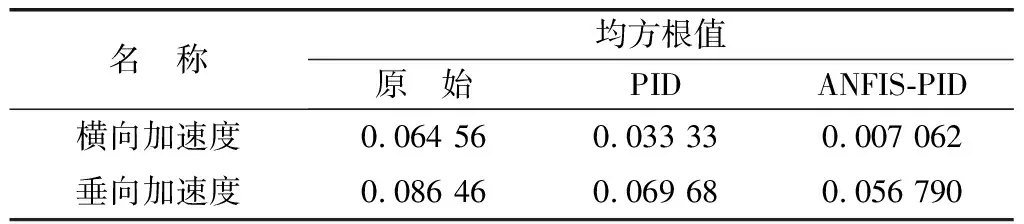
表2 均方根值對比
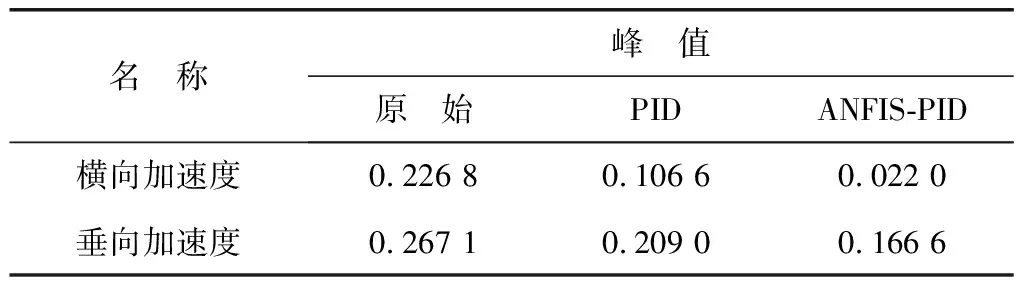
表3 峰值對比
綜上所述,PID控制和ANFIS-PID控制的單軌車輛均優于原始單軌車輛,且ANFIS-PID具有更優異的控制效果,能顯著抑制車輛橫向和垂向振動,提升車輛運行品質。
4 結 論
為提高單軸單軌車輛運行品質,筆者基于單軸單軌動力學模型,構建了ANFIS-PID控制方法。
通過仿真結果表明:相比于原始單軌車輛,PID控制和ANFIS-PID控制的單軌車輛橫向加速度均方根值分別降低了48.37%和89.06%,垂向加速度均方根值分別降低了19.41%和34.32%;橫向加速度峰值分別降低了53.00%和90.30%,橫向加速度峰值分別降低了21.72%和37.60%。說明ANFIS-PID具有更優異的控制效果,為改善單軸單軌車輛運行品質提供了一條新的結構型式和控制方法。

