基于IMM Kalman濾波算法的實時追蹤監控系統

張凱麗 何 玥 程雅茹 孫晨靜 陳亞寧 紀亞芳

（山西師范大學物理與信息工程學院，山西 臨汾 041000）

1 引言

隨著各行各業的飛速發展，國家對人民的人身安全、財產安全的重視不斷提高。視頻監控已經從最初只在特殊行業中使用，發展為各行各業的必備產品。但是在這種社會背景下，依然有不法分子頂風作案，拐賣兒童、入室搶劫等案例仍然存在。

在尋找走失兒童與抓捕罪犯的過程中，最常用的方法是通過監控視頻觀察。監控視頻中記錄了他們犯罪的證據，但是在查看監控回放時，人力監測耗時耗力，容易錯過最佳時期，監測過程難免有疏忽遺漏的地方，因此對監控系統的優化是必要的。針對普通監控系統所存在的缺陷，本文采用SAD匹配算法和IMM Kalman濾波算法，對現有的監控系統進行了優化，實現了對監控范圍內重點目標全程持續跟蹤和信息捕捉，進而完成視頻分析。

2 目標檢測

目前，對收集到的數據進行前期3D 標定的方法為單目視覺或雙目立體視覺。為克服僅使用單目視覺無法對目標精確追蹤的缺點，本文采用雙目立體視覺方式。雙目立體視覺的重點是進行立體匹配，本文通過采用SAD（Sum of Absolute Differences）匹配算法確定左右視圖匹配關系，從而實現雙目立體視覺目標檢測。

SAD匹配算法是將模板圖樣I（尺寸為m*n）與待檢索圖樣I’（尺寸為M*N）進行對比，尋找出最佳匹配圖樣。具體算法步驟如下所示：

（1）將待檢索圖樣和模板圖樣通過卷積神經網絡選擇出所有像素點；

（2）將模板圖樣灰度減去待檢索圖樣灰度，求出二者灰度差之和[1]

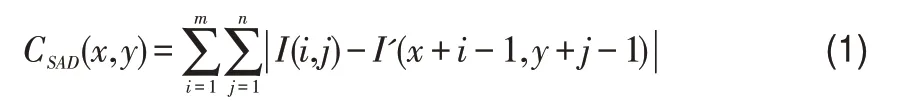
其中i，j 表示子圖的中心坐標，1≤x≤M－m＋1,1≤y≤N－n＋1。

（3）移動模板圖樣，采用(1)中SAD匹配算法選擇出模板圖樣中的所有像素點，并重復步驟(2)；

（4）當SAD值最小時，則為待檢索圖樣的最佳匹配。

3 目標追蹤

目標追蹤算法主要是對目標的外觀進行追蹤，目標外觀不被遮擋屬于理想情況。在實際檢測中，由于受外界因素干擾，目標常會受到遮擋，使追蹤出現失效情況，此時可利用IMM Kalman濾波算法修正失效段，對追蹤過程進行優化。

3.1 有效性判斷

在SAD匹配算法的基礎上，采用一種有效性判斷方法，其方法的一般步驟如下：

（1）將目標檢測時計算的所有SAD值列成矩陣（設模板圖樣T大小為a*b，待檢索圖樣S大小為A*B），則可知矩陣大小為（A-a+1）*(B-b+1)；

（2）找出SAD最小值在矩陣中的位置坐標（x,y）；

（3）在SAD 矩陣中，以最小值（x,y）為中心點，取一個一定大小的矩陣Gi（矩陣Gi的大小不能太小，否則變化不明顯，無法更準確地判斷有效性），用Gi來表示某一幀的圖像。將矩陣分塊，選取不同大小的矩陣，根據選取的矩陣，設置不同大小的權重系數，這就提高了目標跟蹤的準確性，減少了目標跟蹤過程中受到遮擋等干擾因素的消極影響；

（4）模板圖像是從第1幀圖像獲取的，以第1幀圖像對應的G1為依據，與其他幀圖像對應的矩陣Gi采用歸一化互相關的方法進行計算，公式[1]為：

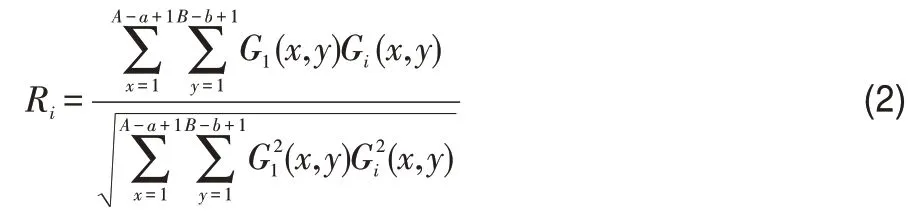
（5）計算模板T的像素平均值[1]：

計算相關性閾值[1]：

將每幀圖像對應的Ri與RT進行比較，若Ri≥RT，則相關跟蹤有效，否則相關跟蹤失效。

3.2 IMM Kalman濾波算法

Kalman 濾波算法是一種利用線性系統狀態方程，通過系統輸入輸出觀測數據，對系統狀態進行最優估計的算法[1]。由于觀測數據中存在系統噪聲和干擾的影響，所以最優估計也可看作是濾波過程。在目標追蹤時，可通過Kalman 濾波算法進行動態估計。當目標的運動模型服從高斯分布時，對其運動狀態進行預測，將預測模型與觀察模型進行對比，根據誤差來更新運動目標的狀態。由于Kalman 濾波算法一般適用于線性系統，而線性系統屬于理想情況，因此在實際應用中存在一些弊端。

本文采用的是IMM Kalman 濾波算法，IMM Kalman 濾波算法是1984年H.A.PBlom基于Kalman濾波算法而提出的一種新型濾波算法。該算法克服了Kalman濾波算法的局限性，通過對多個模型的估計結果進行加權平均，對動態系統進行更優的估計，從而得到更理想的效果。

IMM Kalman濾波算法的一般步驟如下：

（1）設跟蹤目標運動狀態有m種，與之對應m個運動模型，第j個模型可用如下公式[1]表示：

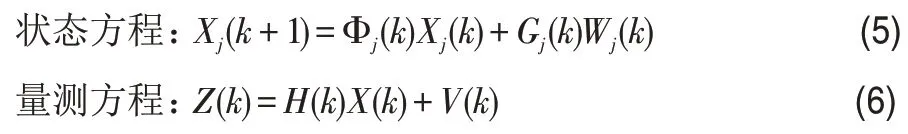
其中Φj(k)是狀態轉移矩陣，Wj(k)～(0,Qj)是滿足高斯分布（均值為0，協方差矩陣為Qj）的白噪聲序列，Gj(k)是噪聲驅動矩陣，H(k)是系統模型，V(k)是觀測噪聲。

（2）m種模型間的馬爾可夫概率轉移矩陣為：

其中pij表示由第i個運動模型轉移到第j個運動模型的概率。

（3）由上一步模型概率μj(k-1)得到模型j的預測概率pj，計算出模型i到模型j的混合概率μij(k-1)，結合目標的狀態估計得出模型j的混合狀態估計，從而得到模型j的混合協方差估計。

模型j的混合狀態估計：

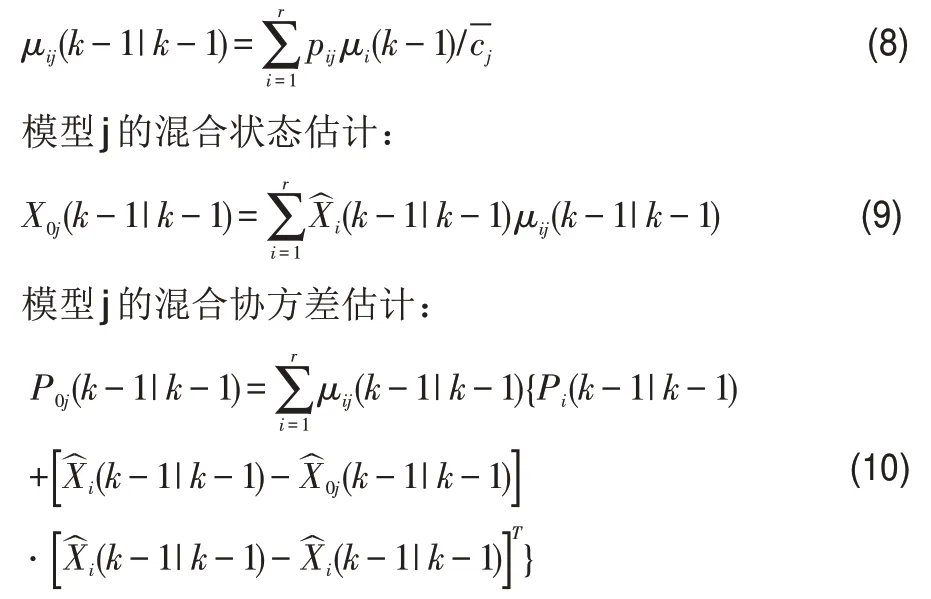
（4）以模型j的混合狀態估計、混合協方差估計以及量測方程Z(k)作為輸入進行Kalman 濾波，更新預測狀態和濾波協方差。

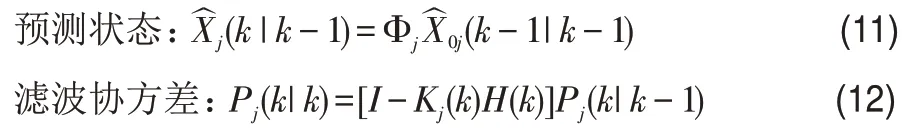
（5）采用似然函數（Likelihood function）對μj(k)進行更新。

模型j的似然函數：

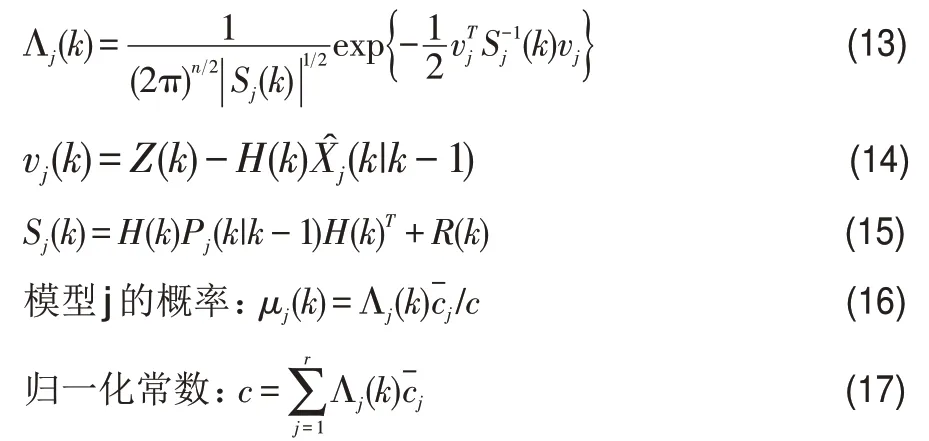
（6）通過對模型j 進行輸出交互，計算多個模型估計結果的加權平均值，得到總的狀態估計和協方差估計。

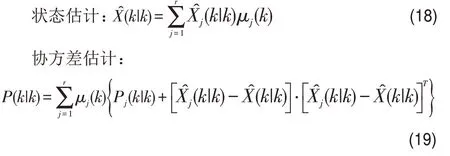
在追蹤監控過程中，采用SAD匹配算法和IMM Kalman濾波算法相結合的方式，不斷更新目標的概率，從而優化目標追蹤的精確度。

4 仿真分析

4.1 SAD匹配算法仿真

用相機平行移動拍攝得到監測目標的左、右兩幅視點圖像，通過MATLAB對SAD匹配算法進行仿真，結果圖1、2所示。

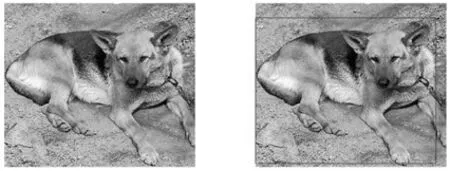
圖1 不受遮擋的監測目標

圖2 受遮擋的監測目標

如圖1、2所示，以左目圖像的源匹配點為中心，定義一個窗口，通過移動右目圖像逐步計算灰度差值，從而尋找最佳匹配點。仿真得到不同狀態下監測目標的檢測結果，當目標不受遮擋和受遮擋時，SAD匹配算法都可以無失真地檢測出目標。由此可見，SAD匹配算法可實現對目標的檢測功能。

4.2 IMM Kalman濾波算法仿真

將目標運動軌跡劃分成三個模型：勻速直線運動（模型一），右轉（模型二），左轉（模型三）。

0～20s，目標向右前方做276m/s 的勻速直線運動；第20s時，改變其運動方向；20s～60s，向左前方做247m/s 的勻速直線運動；第60s時，再次改變目標的運動方向；60s～100s，向右前方做247m/s的勻速直線運動。

圖3為目標運動軌跡追蹤示意圖，由圖可知濾波值與目標真實軌跡偏差較小。

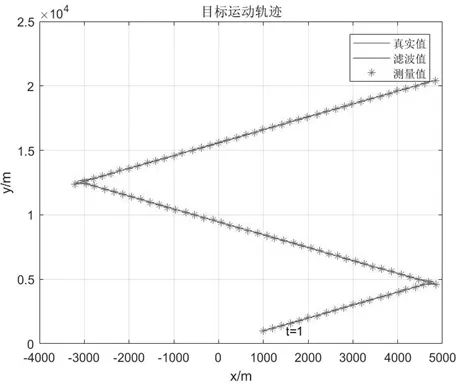
圖3 目標運動軌跡

圖4和圖5分別為追蹤過程中目標位置和速度的誤差分析曲線。從圖中可以看出，目標在做勻速直線運動時，誤差值均在0值附近波動，且時間越長誤差波動幅度越小，越接近0值；當目標方向突然發生改變時，由于時間較短，變動較大，因此誤差值較大；第60s 時相較第20s 時誤差值有所下降。分析仿真結果可得，在追蹤過程中，隨著追蹤時間的延長，追蹤次數的增加，系統的優化效果會逐漸顯著。

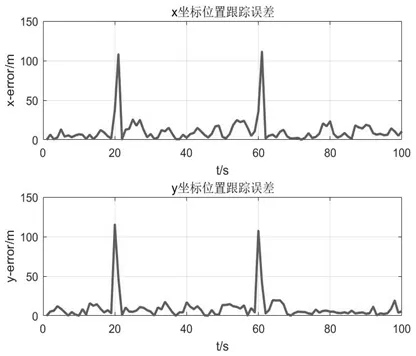
圖4 位置跟蹤誤差

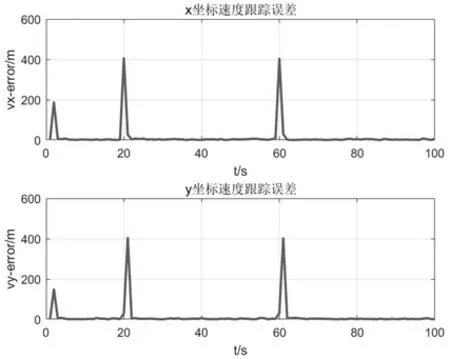
圖5 速度跟蹤誤差

圖6 為IMM Kalman 濾波算法模型概率曲線，從圖中可以看出，在目標做勻速直線運動的過程中，模型一概率接近100%；在20s時目標左轉，模型一概率逐漸降低，模型三概率逐漸提高，最終模型三概率接近100%；60s時刻目標右轉，模型一概率逐漸降低，模型二概率逐漸提高，最終模型二概率接近100%。

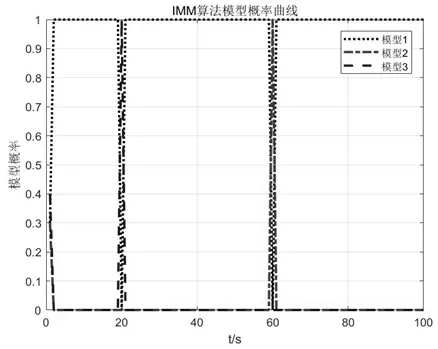
圖6 IMM Kalman濾波算法模型概率曲線

5 結論

由仿真結果可知，SAD 匹配算法能確定目標位置，可以用于目標檢測。IMM Kalman 濾波算法能修復失效段，可以用于目標追蹤。通過仿真軟件進行驗證，結果表明，在監控設備的輔助下，該系統對監控視頻中某目標可以實現檢測與追蹤功能，具有現實意義。但系統尚未進行實物測試，仍停留在仿真研究階段，實際測試情況有待進一步研究。