截面幾何參數(shù)對混凝土薄壁橋塔溫度應力的影響

任 翔，齊 洋，王 璐，黃平明，宋 飛

(1.西安科技大學 建筑與土木工程學院，陜西 西安 710054； 2.長安大學 橋梁與隧道陜西省重點實驗室，陜西 西安 710064)

0 引言

進入21世紀后，大跨徑橋梁得到迅速的發(fā)展，結構跨度不斷增大，混凝土橋墩、橋塔高度逐漸增高，體積逐漸增大。多數(shù)橋梁建成運營后混凝土薄壁箱型橋墩、橋塔出現(xiàn)了豎向裂縫[1-4]。而開裂是大體積混凝土結構中一個影響結構安全性和耐久性的關鍵問題[5]。

相關研究發(fā)現(xiàn)橋塔結構內外表面日照溫差荷載引起溫度應力是導致橋塔開裂的重要因素[6-9]，且裂縫寬度會隨索塔內外表面溫差的變化而變化，發(fā)生閉合和擴展現(xiàn)象[10-13]。表明塔壁內外表面的日照溫差是產生溫度應力的主要原因。因此，日照溫差應力對于混凝土薄壁橋塔結構的影響不可忽視。截面幾何參數(shù)對混凝土薄壁結構塔壁內外表面的溫差應力有較大的影響，其相關研究較少。張運波等[14]分析了雙肢矩形薄壁空心墩不同截面形狀對其溫度應力的影響，發(fā)現(xiàn)溫度應力隨著墩壁截面形狀的變化而變化。傅理文，汪勁豐等[15]以某公路橋方形橋墩出現(xiàn)開裂為背景，通過對圓形、方形、矩形3種截面形狀下的溫度效應進行對比，發(fā)現(xiàn)圓形截面可降低溫度開裂的風險。武利群[16]研究了箱梁截面幾何參數(shù)對箱梁頂板日照溫差應力的影響，發(fā)現(xiàn)頂板越厚、底板越薄、腹板越高，頂板受力越有利。

本研究利用ANSYS的熱分析功能對某混凝土薄壁箱型橋塔溫差應力進行研究，分析幾何參數(shù)對混凝土薄壁橋塔溫差應力的影響，找不同截面幾何參數(shù)影響的敏感性，為該類結構設計提供一定的參考依據(jù)。

1 橋塔結構

研究對象為某跨徑為960 m鋼箱梁懸索橋混凝土橋塔。該橋位于北緯30.57°，東經111.39°，結構方位角為82°。南北塔塔肢均為空心矩形箱結構，南塔承臺以上高度為142.227 m，設3道橫梁，北塔承臺以上高度為112.415 m，設2道橫梁，南北塔頂橫橋方向5 m寬，從塔頂?shù)剿撞蛔儯豁槝蛳? m寬，從塔頂按1∶100的坡度加寬至承臺，塔頂橫橋向等寬為5 m。南、北塔頂部壁厚均為0.7 m，南塔底部寬度為1.0 m，北塔底部壁厚度0.8 m。本研究選取研究截面布置及尺寸如圖1所示。其中圖1(c)中L為順橋走向外側塔壁長度，6～8.84 m；B為橫橋走向外側塔壁寬度，等寬5 m；t為塔壁厚度，等厚0.8 m。

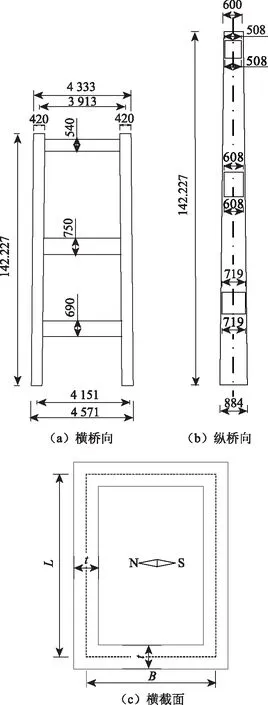
圖1 矩形空心橋塔典型截面(單位：cm)Fig.1 Typical section of rectangular hollow pylon (unit: cm)

2 分析方法

2.1 溫度應力計算方法

結構熱力耦合分析方法有直接法和間接法。直接法考慮了溫度、結構位移自由度，并引入溫度場和應力場的邊界條件，進行一次性的耦合分析。由于高度非線性的橋塔溫度場以及其箱形結構面-面輻射熱分析的復雜性，增加計算難度，且由于力學邊界的不準確性會使結果有一定的誤差。而間接法是根據(jù)熱傳導方程得到節(jié)點熱流率向量，再將其作為荷載引入應力場求解方程，最后通過求解方程計算應力場[17]，如下：

{K}{U}={FR}+{FA}，

(1)

2.2 橋塔有限元模型2.2.1 初始條件

模型初始條件采用橋塔內部溫度及環(huán)境溫度的實測值，塔壁厚度溫差采用一天內正溫差和負溫差最大的時刻作為分析荷載。實測溫差在不同厚度的塔壁處應是不同的，大量學者基于實測數(shù)據(jù)發(fā)現(xiàn)，溫度在橋塔、橋墩等柱狀結構壁厚方向的分布模型一般有直線型、雙折線和指數(shù)分布，其中與指數(shù)分布最為接近[16,18-23]，當壁厚達到一定數(shù)值時，溫度隨厚度變化不大[21-23]。我國鐵路規(guī)范[24]也有類似的規(guī)定，當頂板和腹板厚度≥26 cm時，溫度曲線就趨于穩(wěn)定。本研究通過現(xiàn)場實測數(shù)據(jù)發(fā)現(xiàn)當橋塔壁厚大于0.24 m時溫差變化不大，而文中分析的橋塔壁厚在0.2～1.6 m之間，為了簡化計算，本研究在模擬時只考慮了不同方位上的溫差，對不同壁厚時的溫差進行了簡化處理，方便計算。

2.2.2 邊界條件

有限元模型溫度邊界條件采用第二類邊界條件。第二類邊界條件是已知物體邊界上的熱流密度[25-26]，即

(1)

式中，q(t)為Γ邊界上總的熱流密度，由太陽輻射、對流換熱和長波輻射3部分組成，以熱量流入為正，流出為負；Kn為邊界平面外法線方向的熱傳導系數(shù)；T為溫度。

2.3 橋塔材料參數(shù)及模型

橋塔采用C50混凝土，采用砂巖做骨料，查詢規(guī)范[27]可得，導熱系數(shù)取值為10.6 kJ/(m·h·℃)，比熱容取值為0.96 kJ/(kg·℃)，線膨脹系數(shù)為10-5。有限元模型及結構離散見圖2。混凝土橋塔采用平面有限元模型，單元選擇PLANE42四節(jié)點四邊形單元，網格采用自由劃分，單元長度為0.1 m。

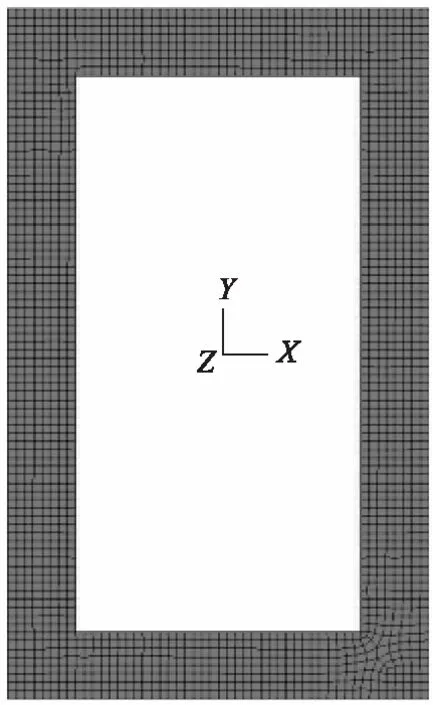
圖2 橋塔塔壁截面網格劃分Fig.2 Meshing of pylon wall section

2015年1月29日至2月4日對某懸索橋混凝土橋塔南塔肢進行了為期一周的溫度場測試，選取了2015年1月30日上午10時和1月31日凌晨2時的正溫差和負溫差作為外荷載，分析不同截面幾何參數(shù)對南側塔壁內外表面溫度應力的影響，如表1所示。

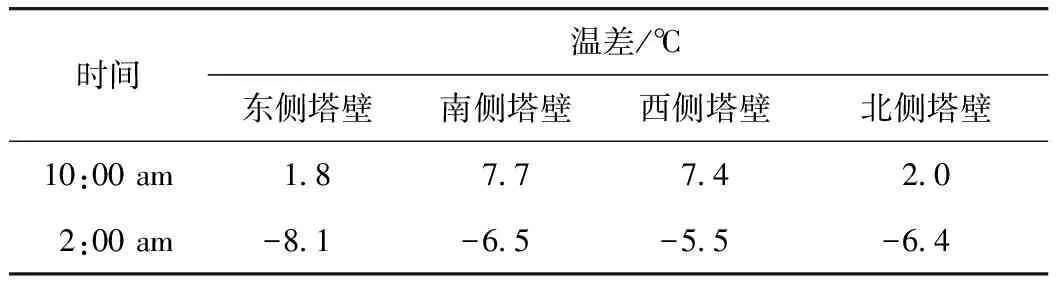
表1 塔壁實測塔壁溫差

溫度荷載以約束的形式施加在橋塔塔壁內外表面，按二維溫度場計算，先求解橋塔截面溫度分布，然后轉化成結構單元求解溫度應力。

3 溫度應力分析

3.1 塔壁厚度對溫度應力的影響

南、北塔壁厚度為t1，東、西塔壁厚度為t2，如圖3所示。通過改變塔壁厚度分析塔壁厚度方向溫差對塔壁內外表面溫度應力的影響。塔壁厚度選擇兩種工況：工況1，4個塔壁厚度均相等；工況2，2個對邊塔壁厚度相等，相鄰2個塔壁厚度不相等。

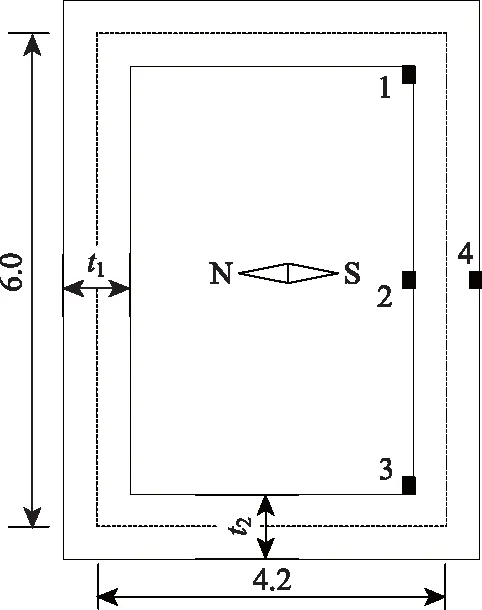
圖3 橋塔溫度應力分析截面及測點(單位：m)Fig.3 Analysis section and measuring points of thermal stress of bridge pylon (unit: m)

3.1.1 等厚度變化

圖3所示，塔壁溫度應力分析截面中線的長度為6.0 m，寬度為4.2 m，且保持不變。t1=t2且從0.2～1.2 m每0.1 m一個等級變化。將塔壁厚度0.80 m的截面作為基準截面，用于與其他不同截面厚度下的溫度應力進行比較分析。塔壁內表面在中線、兩個角隅處及外表面中線處設置了溫度應力觀察點。

(1)塔壁正溫差

圖4給出了正溫差作用下南側塔壁不同厚度的塔壁內側表面溫度應力分布。

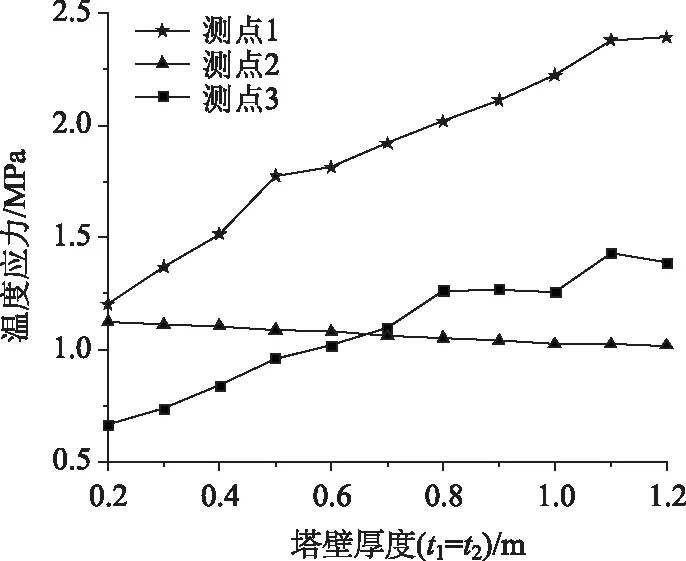
圖4 南側塔壁在不同厚度下內表面應力分布Fig.4 Stress distribution on the inner surface of the south pylon wall under different thickness

圖4可以看出，塔壁正溫差荷載作用下，南側塔壁內表面的最大溫度應力出現(xiàn)在位置1處，且位置1，3處的溫度應力均大于其他位置。

隨著塔壁厚度的增大，南側塔壁位置1，3處的溫度應力逐漸增大。當塔壁厚度為0.8 m(基準截面)時，位置1，3處的溫度應力分別為2.03 MPa和1.26 MPa；當塔壁厚度為0.2 m時，位置1，3處的溫度應力分別為1.19 MPa和0.66 MPa，相比于基準截面減小約41%和48%；而塔壁厚度為1.2 m時，溫度應力分別為2.39 MPa和1.38 MPa，相比基準截面增大約15%和9.5%。位置2處的溫度應力隨著壁厚的增大而逐漸減小，且變化較為緩慢。綜上可知，塔壁等厚度變化對南側塔壁內表面角隅處的溫度應力的影響較大。

(2)塔壁負溫差

圖5給出了負溫差下南側塔壁不同厚度的塔壁外側表面溫度應力分布。

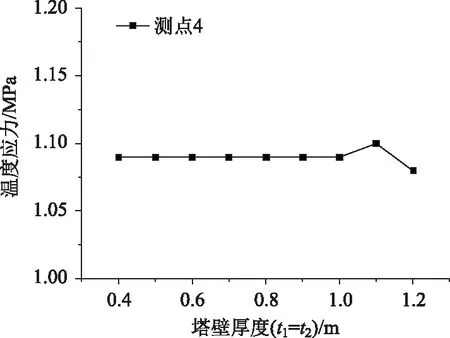
圖5 南側塔壁不同厚度下外表面溫度應力Fig.5 Thermal stresses on outer surface of south pylon wall with different thicknesses

由圖5看出，在負溫差作用下，4個塔壁等厚度變化對南側塔壁外表面位置4的溫度應力影響很小。

3.1.2 不等厚度變化

橋塔溫度應力分析截面及測點仍采用圖3所示截面，基準截面塔壁厚度t1=t2，其對比截面塔壁厚度t1≠t2。t2保持不變取值為0.8m，t1變化，塔壁厚度比t1/t2分別取0.5，0.6，0.8，1.2，1.5，1.8和2.0變化。

(1)塔壁正溫差

圖6給出了相鄰塔壁不同厚度比對南側塔壁內側表面上溫度應力的影響。

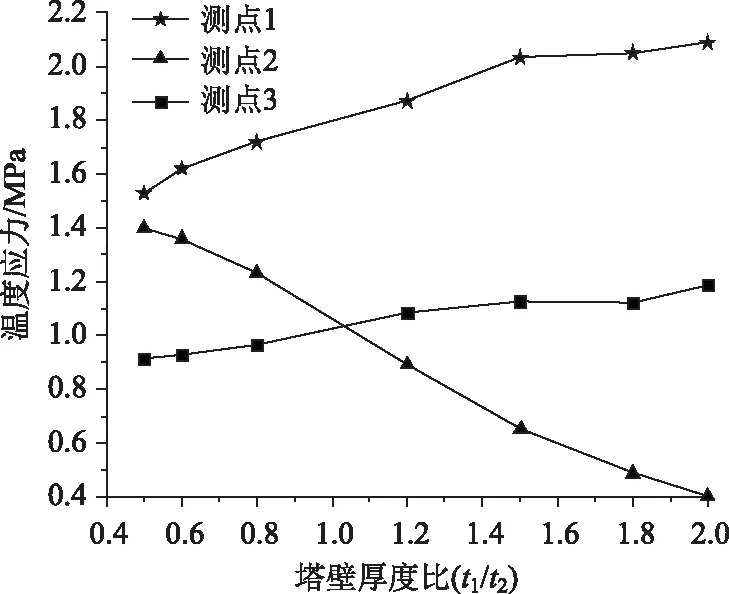
圖6 不同厚度比下南塔壁內表面的溫度應力Fig.6 Thermal stresses on inner surface of south pylon wall with different thickness ratios

由圖6可以看出，相鄰塔壁不同厚度比下，塔壁正溫差荷載引起的最大溫度應力仍出現(xiàn)在南側塔壁內表面測點1處，同時內表面測點1，3處的溫度應力均比其他位置處的溫度應力大。

隨著塔壁厚度比的逐漸增大，南側塔壁內表面測點1，3處的溫度應力也隨之增大，而內表面測點2處及其他位置處的溫度應力隨塔壁厚度的增大而逐漸減小。

與基準截面(t1/t2=1)，當塔壁厚度比為0.6時，南側塔壁1，3處的溫度應力分別降低了約16%和14%，位置2處的溫度應力增大約為22%；當塔壁厚度比為2.0時，南側塔壁1，3處的溫度應力分別增大了約7%和8.5%，位置2處的溫度應力減小約63%。

塔壁內表面測點1，3處的溫度應力的變化幅度比塔壁內表面中心處的溫度應力的變化幅度要小。增大塔壁厚度比可以大幅度地減小南側塔壁內表面中心位置處的溫度應力，但同時增大了角隅處的溫度應力。因此，在選擇塔壁厚度比時，不宜太大。

(2)塔壁負溫差

圖7給出了相鄰塔壁不同厚度比對南側塔壁外側表面上溫度應力的影響。

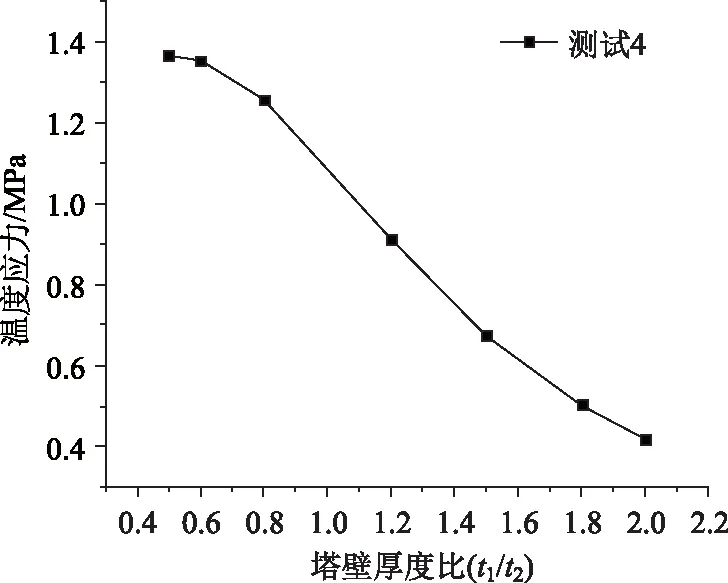
圖7 不同厚度比下南側塔壁外表面溫度應力Fig.7 Thermal stresses on outer surface of south pylon wall with different thickness ratios

圖7可以看出，南側塔壁外表面位置2的溫度應力隨厚度比t1/t2的增大而逐漸減小，變化幅度較大。在正溫差下位置4處的溫度應力與圖6中位置2處的溫度應力結果相似。

3.2 塔壁長寬比對溫度應力的影響

圖1所示，橋塔溫度應力分析截面的4個塔壁厚度均為0.8 m，且保持不變。東側和西側塔壁截面中線長度為B，保持B=4.2 m不變，南側和北側塔壁截面中線長度為L，L變化。

基準截面尺寸為L=4.2 m，B=4.2 m，其余對比截面塔壁截面中線處的長寬比L/B分別取1，1.2，1.5，1.8，2.0，2.2和2.5，分別計算相應的溫度應力，并與基準截面下的溫度應力進行對比分析。塔壁溫度應力觀察點仍參照圖3。

(1)塔壁正溫差

圖8給出了塔壁不同長寬比下正溫差荷載對南側塔壁內側表面上溫度應力的影響。

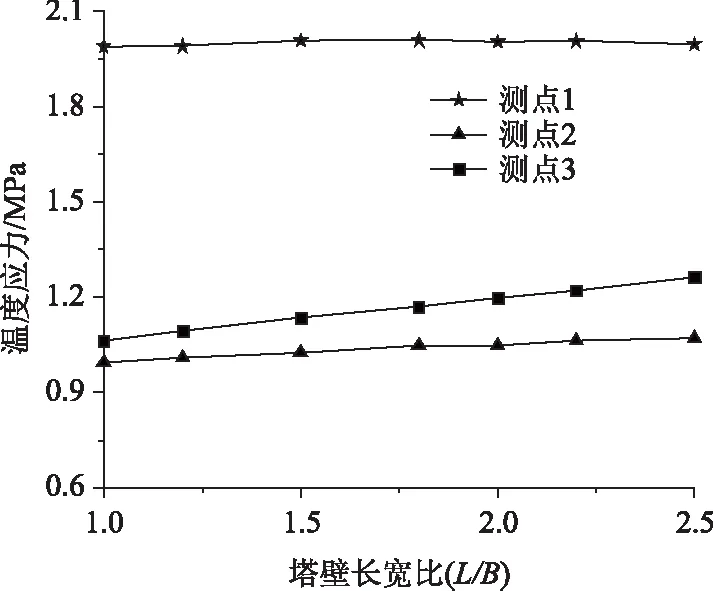
圖8 南側塔壁內表面溫度應力Fig.8 Thermal stress on inner wall surface of south pylon wall

圖8可以看出，改變塔壁截面長寬比對改善塔壁截面溫度應力的效果不明顯。

(2)塔壁負溫差

圖9給出了塔壁不同長寬比下負溫差荷載對南側塔壁外側表面的溫度應力的影響。

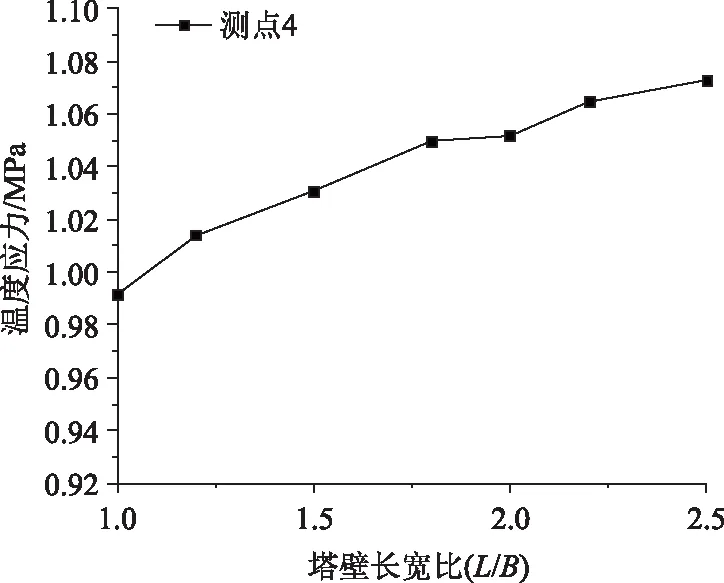
圖9 南側塔壁外表面溫度應力Fig.9 Thermal stress at outer wall surface of south pylon wall

圖9可以看出，負溫差作用下，塔壁長寬比對塔壁外表面的最大溫度應力的影響非常小，這與正溫差作用下的結果是一致的。

3.3 塔壁截面不同倒角對溫度應力的影響

從前面分析可以看出，在塔壁內側表面角隅處存在溫度應力集中現(xiàn)象，為了減小結構在截面角隅處產生的應力集中現(xiàn)象，采用角隅處倒角的方式來降低應力集中。

塔壁截面倒角擬選擇兩種工況：工況1，只對內側截面角隅處倒角；工況2，對內側、外側截面角隅處同時倒角。

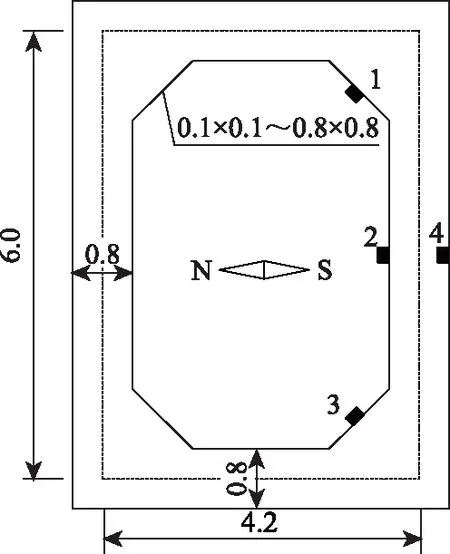
圖10 內表面角隅處倒角及溫度應力觀察點(單位：m)Fig.10 Chamfering at corners of inner surface and observation points of thermal stress (unit: m)

3.3.1 內側截面角隅處倒角

如圖10所示，橋塔塔壁中線長度為6.0 m，寬度為4.2 m，4個塔壁厚度為0.8 m，且保持不變。基準截面為內表面未倒角，對比截面為內表面4個倒角相同，且倒角尺寸從0.1 m×0.1 m到0.8×0.8 m每0.1 m一個等級變化。

(1)塔壁正溫差

圖11給出了正溫差荷載作用下內表面角隅處不同倒角的南側塔壁內側表面上溫度應力分布。

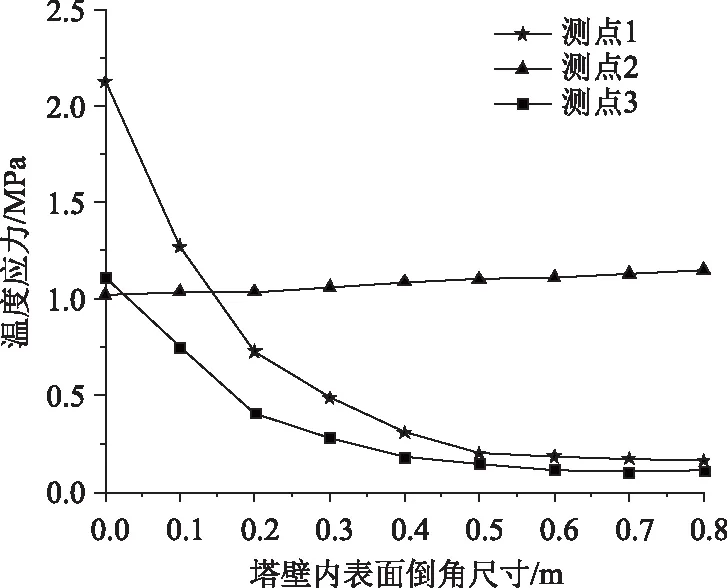
圖11 不同截面倒角下南側塔壁內表面溫度應力分布Fig.11 Distribution of thermal stresses at inner surface of south pylon wall under different sectional chamfers

圖11可以看出，塔壁內側表面角隅處倒角后，南側塔壁內側表面1，3處的溫度應力均比基準截面的溫度應力大幅度減小。

當?shù)菇浅叽鐬?.1 m×0.1 m～0.3 m×0.3 m范圍變化時，角隅處的溫度應力下降較大，當?shù)菇浅叽鐬?.3 m×0.3 m時，相對于基準截面，測點1的溫度應力2.14 MPa降低到0.74 MPa，減小約65%；測點3的溫度應力從1.13 MPa降低到0.42 MPa，減小約63%。

當?shù)菇浅叽绯^0.5 m×0.5 m時，角隅處的溫度應力變化不明顯。除角隅處，其他部位的溫度應力隨著倒角尺寸的增大而增大，但增大幅度較小。表明在塔壁內側表面角隅處倒角能有效地降低角隅處的應力集中，但較大的倒角尺寸增大截面厚度且增加了混凝土用量，造價提高。

(2)塔壁負溫差

圖12給出了負溫差荷載作用下外表面角隅處不同倒角的南側塔壁內側表面上溫度應力分布。

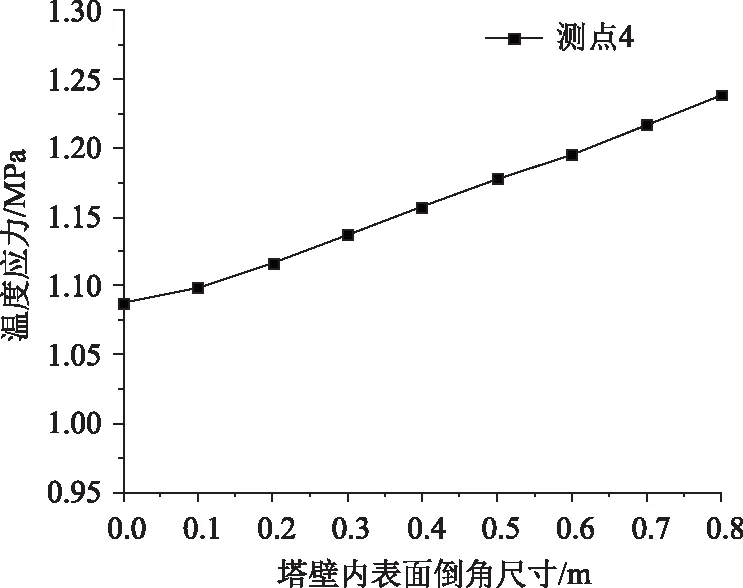
圖12 不同截面倒角下南側塔壁外表面溫度應力Fig.12 Distribution of thermal stresses at outer surface of south pylon wall under different sectional chamfers

圖12可以看出，隨著塔壁內側表面倒角尺寸的逐漸增大，南側塔壁外側表面溫度應力也隨之增大。與基準截面計算結果相比，當?shù)菇浅叽鐬?.8 m×0.8 m 時，其塔壁外表面位置4處的溫度應力從1.09 MPa增大到1.24 MPa，增大約12%。由此表明，負溫差狀況下在塔壁內側表面4個角隅處倒角會增大表面溫度應力，但是增大幅度不大。

3.3.2 內、外兩側截面角隅處倒角

在圖10的基礎上增加了外表面角隅處的倒角，倒角尺寸從0.05 m×0.05 m到0.4 m×0.4 m，每0.05 m一個等級變化，與外側倒角從0.1～0.8 m變化相對應，共8個工況，初始工況為內外側均未倒角。如圖13所示。

圖13 內外兩側截面角隅處倒角(單位：m)Fig.13 Chamfers at inner and outer corners in cross-section (unit: m)

(1)塔壁正溫差

圖14給出了內、外表面倒角在正溫差下南側塔壁內側表面上的溫度應力分布。

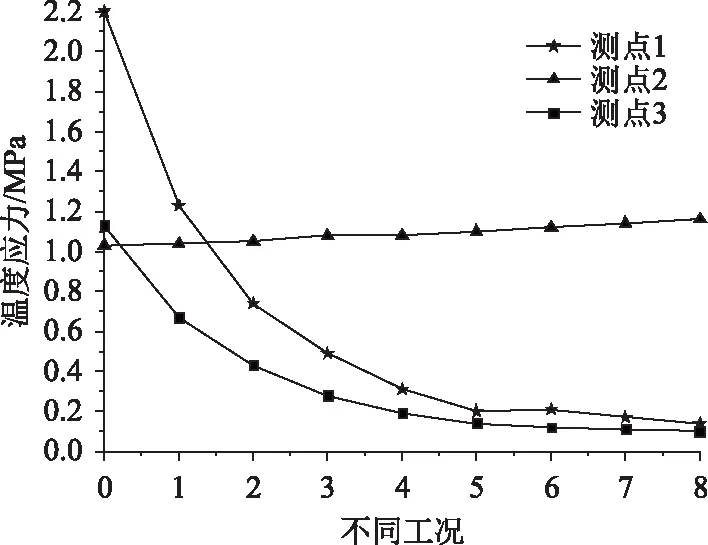
圖14 南側塔壁內表面溫度應力Fig.14 Thermal stress on inner surface of south pylon wall

圖14可以看出，塔壁內、外表面角隅處倒角對南側塔壁內表面的溫度應力的影響與內側表面角隅處倒角的分析結果幾乎一致。

(2)塔壁負溫差

圖15給出了內、外表面倒角在負溫差下南側塔壁內側表面上的溫度應力分布。

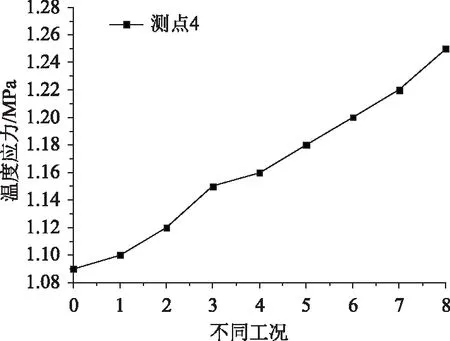
圖15 南側塔壁外表面溫度應力Fig.15 Thermal stress on outer surface of south pylon wall

圖15可以看出，在負溫差作用下，塔壁內外兩側表面角隅處倒角尺寸對南側塔壁外表面位置4處的溫度應力的影響與內側表面角隅處倒角的分析結果一致。

4 結果分析

前述研究發(fā)現(xiàn)，塔壁厚度比t1/t2以及倒角的大小是影響橋塔截面溫度應力的重要因素。但截面參數(shù)的變化會改變混凝土的體積和抗壓剛度發(fā)生變化。因此，設計橋塔截面時需要綜合考慮降低溫度應力和增加橋塔造價兩個因素。

4.1 塔壁厚度

3.1.2節(jié)分析表明，在正負溫差下，塔壁厚度比t1/t2已經成為影響塔壁表面溫度應力的重要因素。因此，在不同塔壁厚度比t1/t2情況下，對混凝土體積和南側橋塔的抗壓剛度(EA)進行分析。

在表2中，混凝土體積和橋塔抗壓剛度隨著塔壁厚度比的增長而快速增長。對比參考截面(塔壁厚度比為1)，當塔壁厚度比為2時，2位置處(僅列出正溫差下的結果)的溫度應力減小了大約63%，同時混凝土體積和橋塔抗壓剛度分別增長了59.7%和64.6%。然而，當塔壁厚度比為0.5時，溫度應力增加約27.1%，而混凝土體積和橋塔抗壓剛度分別下降了約29.8%和32%。結果表明，較大的塔壁厚度比可以降低橋塔中心處溫度應力，但同時會導致角隅處溫度應力集中，混凝土體積增加，塔壁長寬比變小，從而導致橋塔的抗壓剛度降低。

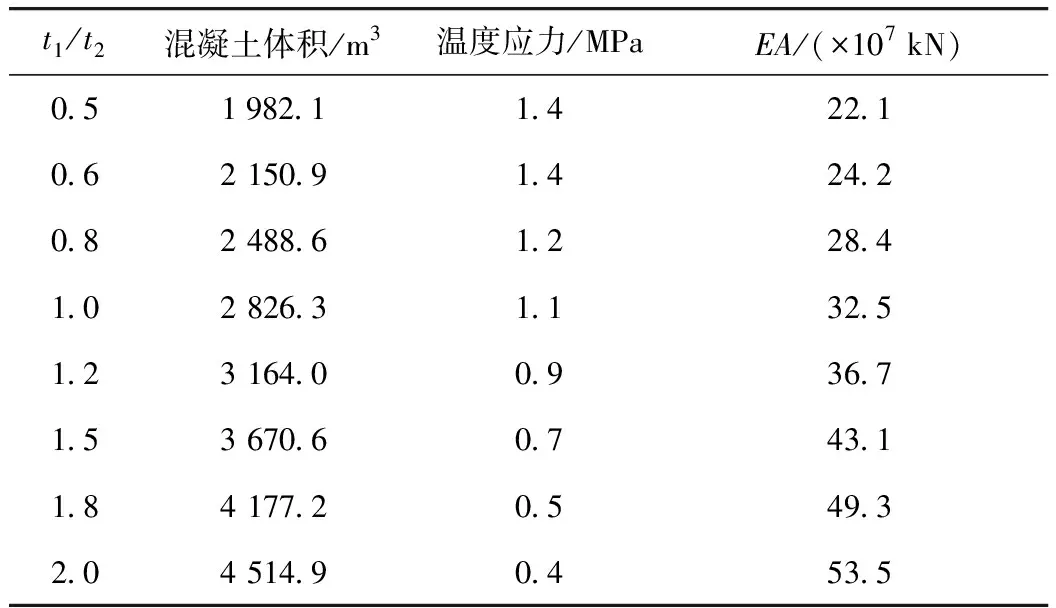
表2 塔壁不同厚度比條件下橋塔的混凝土體積、溫度應力 和抗壓剛度

4.2 內側截面角隅處倒角

第3.3節(jié)分析表明，倒角可以大大減少南塔壁內表面角隅的溫度應力。表3顯示了不同倒角尺寸下，橋塔的混凝土體積、溫度應力和抗壓剛度。

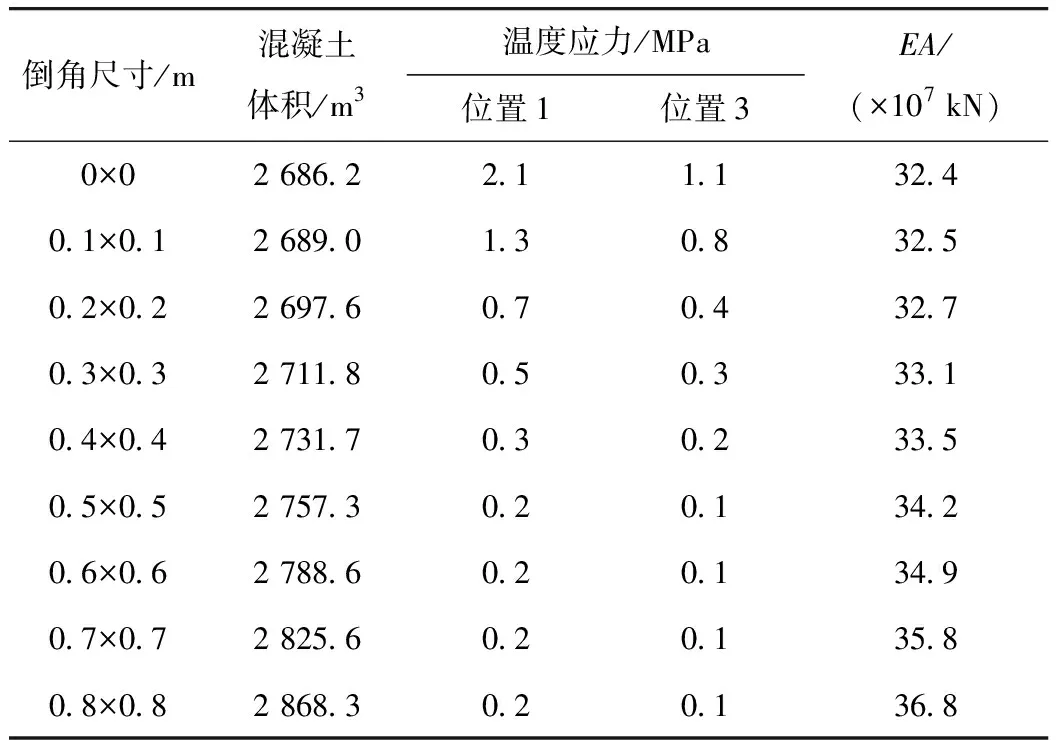
表3 不同倒角尺寸條件下橋塔的混凝土體積、溫度應力和 抗壓剛度

與參考截面(無倒角)相比，當?shù)菇谴笮?.1 m×0.1 m變化到0.3 m×0.3 m(如表3所示)，位置1和3處的溫度應力會迅速減小。當?shù)菇浅叽绱笥?.3 m×0.3 m時，橋塔的混凝土體積增加約 1%。當?shù)菇谴笮∽優(yōu)?.5 m×0.5 m時，位置1和3處的溫度應力基本保持不變，但混凝土體積仍隨著倒角變大而繼續(xù)逐漸增大；當?shù)菇窃?.3 m×0.3 m～0.5 m×0.5 m之間時，改變倒角尺寸對于溫差應力及混凝土體積的影響均較小，因此建議在此區(qū)間內選取倒角尺寸。

5 結論

為了降低混凝土橋塔內外表面溫度應力，本研究介紹了橋塔截面幾何參數(shù)，如塔壁厚度、塔壁長寬比和倒角大小，對混凝土橋塔的溫度應力的影響。結果如下：

(1)塔壁厚度比t1/t2是重要設計參數(shù)，其取值不宜太大；

(2)改變塔壁截面長寬比對改善塔壁截面溫度應力的效果不明顯；

(3)倒角應設計在內側截面角隅處，其尺寸建議在0.3 m×0.3 m～0.5 m×0.5 m之間進行取值。