基于雙層規劃模型的應急救援調度與路徑選擇集成優化

姚 佼，邵楚薇，鮑雨婕，李宇航

(上海理工大學 管理學院，上海 200093)

0 引言

城市化進程的加劇，城市多種功能的聚集化，突發應急事件發生的概率不斷上升，如何降低其發生后的人員傷亡和財產損失值得關注[1]。救援時間作為應急交通的關鍵參數，一直是應急交通管理的主要目標，相關的研究表明，路網應急交通產生前的車輛調度，及產生后在路網中路徑選擇對其影響尤為顯著[2]。因此，如何將二者進行有效的集成，針對不同類型應急救援車輛，精準施策，進行有效的集成，對于降低突發事件的影響，減輕其發生后果的嚴重性，具有十分重要的意義。

對不同類型應急救援車輛的合理地調度，并對其在路網的行駛路徑進行優化，一直是應急交通系統優化的研究熱點和難點。關于應急車輛調度，?zdamar等[3]對自然災害下應急救援中多階段的救災物資配送問題進行了研究，并結合拉格朗日松弛法對動態救災模型進行分析求解；計雷[4]提出應急調度救援的本質是運輸費用成本和時間成本，因此他將模型簡化為多目標優化問題并求最優解；在應急交通的路徑選擇方面，Potvin等[5]以突發事件為背景，研究了應急救援車輛路徑問題，并且解決一個考慮客戶實時請求和車輛動態行駛時間的時間窗動態車輛路徑問題；劉勇等[6]根據基本蟻群模型，進行了最優路徑蟻群模型的改進研究，在蟻群算法的轉移概率中引入路徑權重，得到了應急救援的最優路線，同時結合調度路徑優化問題進行了多方面的考慮。

雙層規劃模型綜合考慮了上下兩層目標的協調，從而可以取得整個系統的最優解。Calvete等[7]基于此，構建了以生產調度問題為核心的雙層規劃模型，上層模型的目標是將時間成本和費用成本最小化，下層模型將生產成本最小化，并結合蟻群算法對模型進行求解；楊忠振等[8]建立的配送選擇與路徑優化雙層規劃模型，證明其可以有效降低配送系統的總成本，提高了配送的整體效率。在應急救援交通的管控中，若單獨從一個角度進行優化，會因為考慮不夠全面，無法得到整體最優的決策方案。只有將調度與路徑問題綜合考慮,彼此反饋，全面協調應急救援中的各個環節，才能針對應急救援城市道路的特點制訂成熟的、實時的應急救援方案。本研究綜合雙層規劃模型在生產調度、物流配送及路徑優化等方面的效果，根據不同應急救援車輛類型，結合路網交通狀態的動態變化[9]， 將應急救援的調度和路徑選擇進行集成，構建相應的雙層規劃模型，并進行求解。

因此，本研究的重點主要聚焦在：

(1)基于城市應急救援事件發生后，針對不同應急救援車輛類型進行調度，以及動態路網下應急車輛最優路徑選擇問題，提出了基于雙層規劃的應急救援調度與動態路徑集成優化模型。

(2)采用基于非優勢排序和精英策略的遺傳算法和改進蟻群對模型進行求解。

(3)通過實際的案例分析與驗證，驗證模型在減少應急車輛的調度成本、在途行程時間、降低路網擁堵程度等方面的實用性。

1 應急救援調度和路徑選擇的目標分析

應急救援的主要目標是盡可能降低突發事件造成的影響[10]，同時讓應急交通能在最短時間內抵達事故發生點。因此，應急救援主要從應急交通的調度和路徑動態選擇兩方面進行考慮。其中，應急車輛的調度是一個涉及多因素的復雜問題[11]，不僅要兼顧應急救援時間，還要考慮受到出救小區資源調度分配的公平性、路徑費用、救援不及時造成的損失等多方面的影響。本研究考慮單應急救援請求點、多應急出救點、不同類型應急救援車輛(如消防車、救護車、公安警車、工程搶險車)[12]，在應急調度階段，將優化的主要目標分為3個：以最小的時間成本實現對應急救援請求點的響應、以最小的固定成本實現各出救小區的選擇、以最優的容量成本限制求解各出救小區中不同類型應急車輛的調度數量；在路徑選擇階段，則重點考慮應急車輛到達救援點的時間盡可能短[13-14]，即不僅考慮救援路徑沿線的交叉口數量，及信號延誤時間，還需要加入救援路徑上的動態交通狀態的影響。

基于上述目標的分析，考慮將應急救援的車輛調度和路徑選擇結合，建立雙層規劃模型，進行集成優化，其中上層應急調度中的時間成本是在下層路徑行程時間的基礎上，考慮不同出救點的車輛數量計算得到，其固定成本反映了各個應急小區的車輛出動情況，也會影響下層的路徑選擇，從而最終影響行程時間，上下兩層間的目標不斷相互反饋，最終結果趨于最優解，模型的研究流程如圖1所示。

圖1 應急救援交通調度與路徑優化集成的雙層規劃 模型研究流程Fig.1 Flowchart of studying bi-level programming model of integrated traffic scheduling and route optimization of emergency rescue

2 模型描述

應急救援的調度與路徑選擇可以看作是一個雙層規劃[15]，為降低研究的復雜性，本研究設計不同類型應急救援車輛的出動位置以交通小區為單位進行劃分，并根據該交通小區相應半徑范圍內是否存在車輛的集合地(如救護車的出動是考慮小區內是否存在醫院以及數量，消防車考慮小區內是否存在消防站及其數量，工程搶險考慮小區內是否存在市政搶險單位及其數量)，來確定該出救小區是否能出動相應類型的應急車輛進行救援。

決策部門根據各類應急交通資源的所處交通小區的位置，以及已知應急救援請求點的需求，在允許的各類應急車輛數約束下確定最佳的應急車車輛調度方案；對于各類應急車輛在出救點和救援請求點之間的路徑選擇，考慮路網交通狀態的變化，動態優化應急交通的出行路徑[16]。以最優化應急救援交通調度評價函數和最優路徑選擇評價函數為目標[17]，采用雙層規劃的建模方法[18]，構建了動態的調度與路徑選擇的集成優化模型[19]。

考慮研究問題的復雜性，模型的建立進行了如下的假設：(1)救援請求點、出救點所在交通小區的地理位置，以及需要各類應急救援交通的車輛數均已知，且不存在變化；(2)路網中所有路段均連通，且路段長度、道路通行能力等參數均已知；(3)應急救援交通車輛類型較多，本研究選取較為關鍵的3類應急救援車輛類型進行研究；(4)本研究出現的各類型應急救援車輛的速度已知而且固定，終點均為救援請求點，且不考慮完成救援任務后的返回；(5)相同類型的應急車輛在救援中假定同時出動，不考慮車輛出動順序。

2.1 上層模型構建

上層主要從應急救援車輛調度過程中的固定成本、容量成本和救援時間成本3個方面進行分析，構建不同類型應急救援車輛的調度模型。具體而言：

目標函數：

ck(t)。

(1)

約束條件：

(2)

(3)

(4)

(5)

(6)

(7)

λp={0,1}。

(8)

模型中有兩類符號,決策變量和模型參數。

其中，決策變量：λp為出救小區p是否派出車輛進行救援，如果是λp=1，否則λp=0。

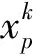
在上層規劃中，式(1)的目標函數為最小化應急車輛調度的整體費用成本(包括固定成本、容量成本和時間成本)；式(2)的約束表示各出救小區是否參與救援的判斷參數；式(3)的約束表示該出救小區中同一救援車輛類型的容量限制判斷參數；式(4)的約束表示應急車輛出救小區中可自由調度的車輛總數不能小于實際參與調度的車輛總數; 式(5)的約束表示實際出救小區中調度的各類應急車輛總數等于救援請求點的車輛需求總量；式(6)的約束表示至少要選擇一個出救小區進行應急救援；式(7)的約束表示選擇應急車輛出救小區的總費用不能大于應急救援小區的總固定成本上限；式(8)為決策變量的取值約束。

2.2 下層模型構建

下層主要從應急救援車輛出動救援時的路段行程時間和信號延誤時間兩個方面進行分析，構建不同類型應急救援車輛的動態路徑選擇模型。該模型基于救援前制定的靜態最優路徑，并根據實時路網交通狀態調整最優路徑[20]。因此，本研究固定的時間間隔，采用馬爾可夫過程對路網交通狀態進行預測[21]，不同類型應急車輛出動前，根據時變的路徑信息，更新下一步的優化救援路徑，直至到達救援請求點。

具體目標函數為：

(9)

約束條件：

(10)

(11)

(12)

(13)

(14)

模型主要包含兩類符號,決策變量和模型參數。

模型參數：T′p為從p出救小區到事故發生點的在途行程時間；Tc為不同類型救援車輛在交叉口(路網拓撲中的節點)的延誤時間，具體的延誤時間計算參考經典的交叉口延誤模型[22]；tij為應急車輛從節點i行駛到節點j的行程時間；fZ(Δtl)為表示路徑交通狀態參數；Δtc為交叉口等待的時間差；kij(Δtl)為時間間隔Δtl路徑ij的交通狀態影響值。

在下層規劃中，式(9)目標函數最小化應急車輛路段行程時間的在途行程時間(包括路段行程時間和信號延誤時間)；式(10)的約束表示應急車輛從每個出救小區至救援請求點，均得到一條最優路徑; 式(11)的約束為交通狀態影響值的求解；式(12)約束為應急車輛路徑的連續性限制，如果救援車輛從一個節點進入，也應從同一個節點離開；式(13)和(14)均為變量取值的約束。

3 模型求解

本研究上下層模型分別建立在NSGA-II算法和改進蟻群算法的基礎上，結合全局搜索進行最終結果的求解。首先，從下層應急車輛最優路徑選擇著手，篩選出符合條件的最優路徑，然后，將結果代入上層應急車輛調度中，由此，得到所有類型應急車輛最優路徑結果均相同的雙層規劃最優解；由于某一類型的應急車輛出動救援，路網交通狀態可能發生變化，因此需不斷更新下層路徑選擇最優解，并將更新結果反饋給上層調度模型；如此循環往復多次，如果在一定的迭代次數內，全部類型的應急救援車輛均已出動，且當前上層調度的費用成本和下層路徑選擇的時間成本的總最優解均不發生改變，則終止計算，輸出當前上、下層的最優解[23]，作為雙層規劃模型的最優解。具體的模型求解流程如圖2所示。

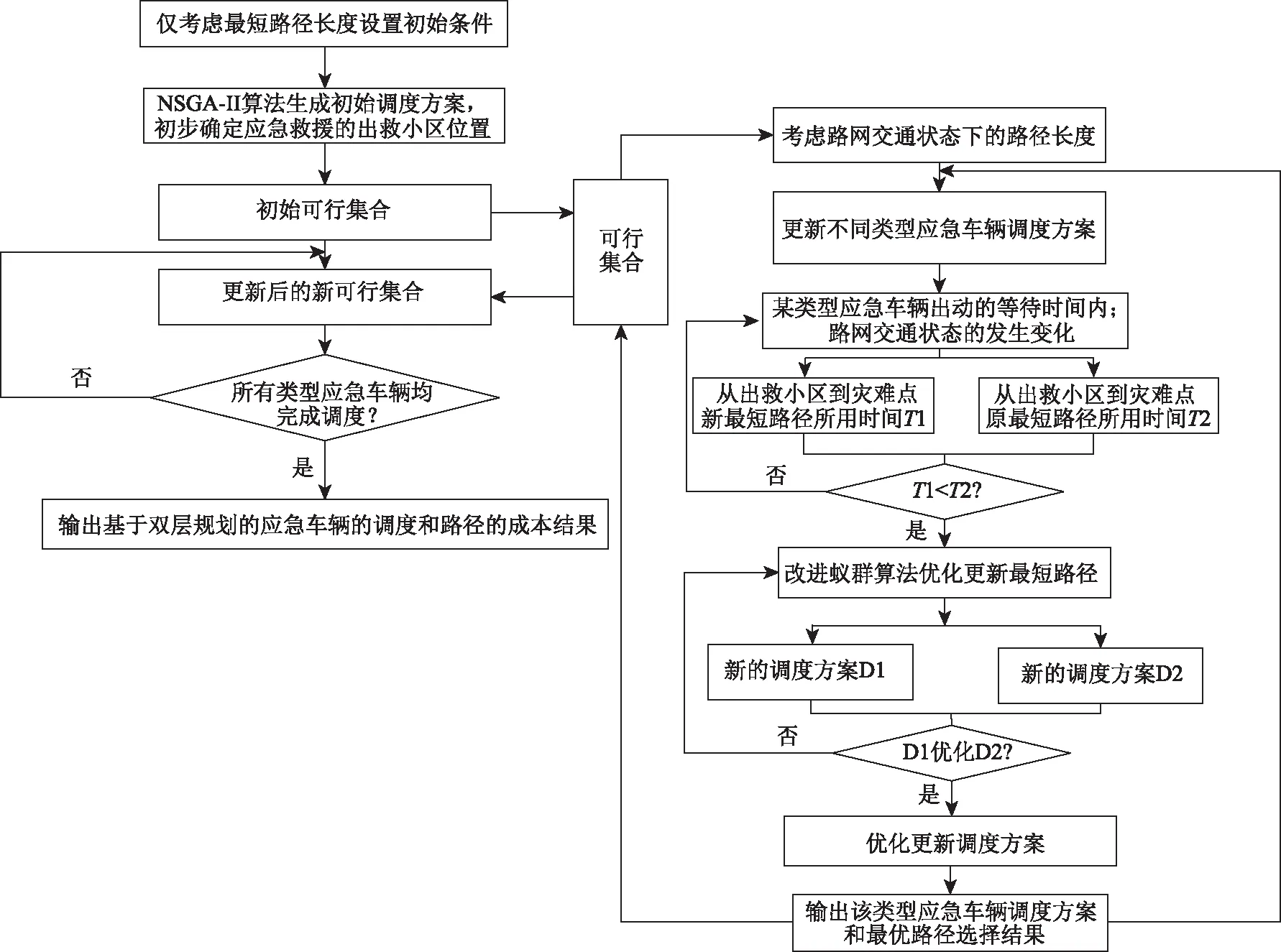
圖2 調度和路徑優化集成的雙層規劃模型的求解流程Fig.2 Flowchart of solving bi-level programming model of integrated traffic scheduling and route optimization

4 案例分析與驗證

選取江蘇省蘇州市工業園區相關實際路網，模擬高峰時段轄區內第五元素網球場突發火災的緊急救援交通調度和路徑優化進行案例分析研究。

根據相關的信息統計，路網共有36個路段節點，55條相交路段。

根據蘇州的實地建筑分布情況，以及該交通小區半徑范圍300 m內是否存在醫院、公安派出所和消防站，明確消防車、救護車、警車等各類應急車輛的出救小區位置。據此根據實地的調查，案例路網中存在5個應急車輛不同類型的出救小區，具體的分布如圖3所示。

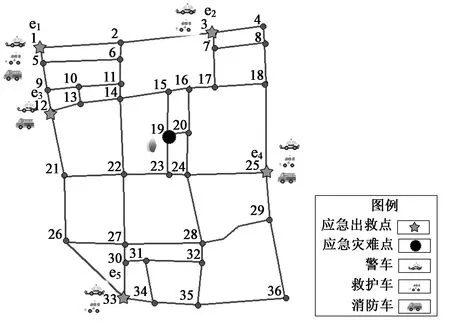
圖3 案例路網及各類型應急車輛的出救小區分布Fig.3 Road network of case study and distribution of emergency vehicles’ rescue zones

結合火災發生時間段(工作日上午8時—9時)的路網交通狀態等相關信息，確定應急救援分配和應急車輛動態最優路徑選擇，并根據前述的雙層規劃模型和求解算法，進行仿真驗證。

基于歷史統計數據，進行相關的參數標定，相應參數設置如下:

(1)需求點和出救小區：發生火災的救援請求點用節點19#表示；根據附近公安派出所、消防站和醫院的相應位置，確定應急車輛出救小區重心的分布，確定各類應急車輛的出救起始節點，標記為節點1#，3#，12#，21#和33#，并根據實際數據，調查各出救小區各類應急車輛的可供應量，如表1所示。

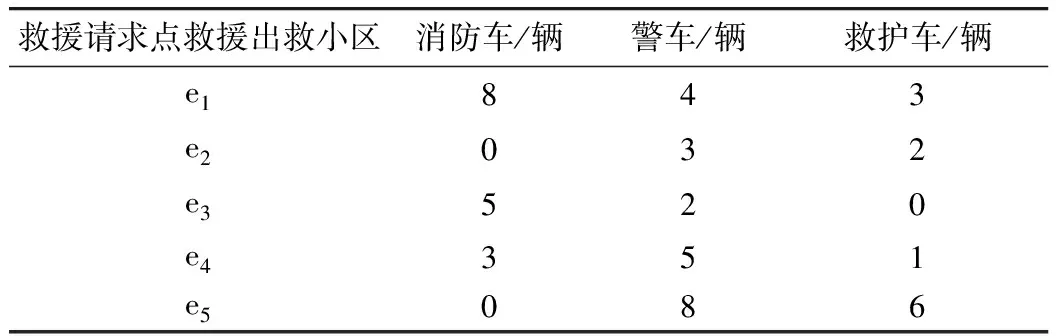
表1 各出救小區的應急車輛資源分布Tab.1 Distribution of emergency vehicle resources in each rescue zone

(2)道路網絡配置參數：統計案例路網的相關靜態參數，調查相應道路的交通量，各路段相關參數如表2所示。

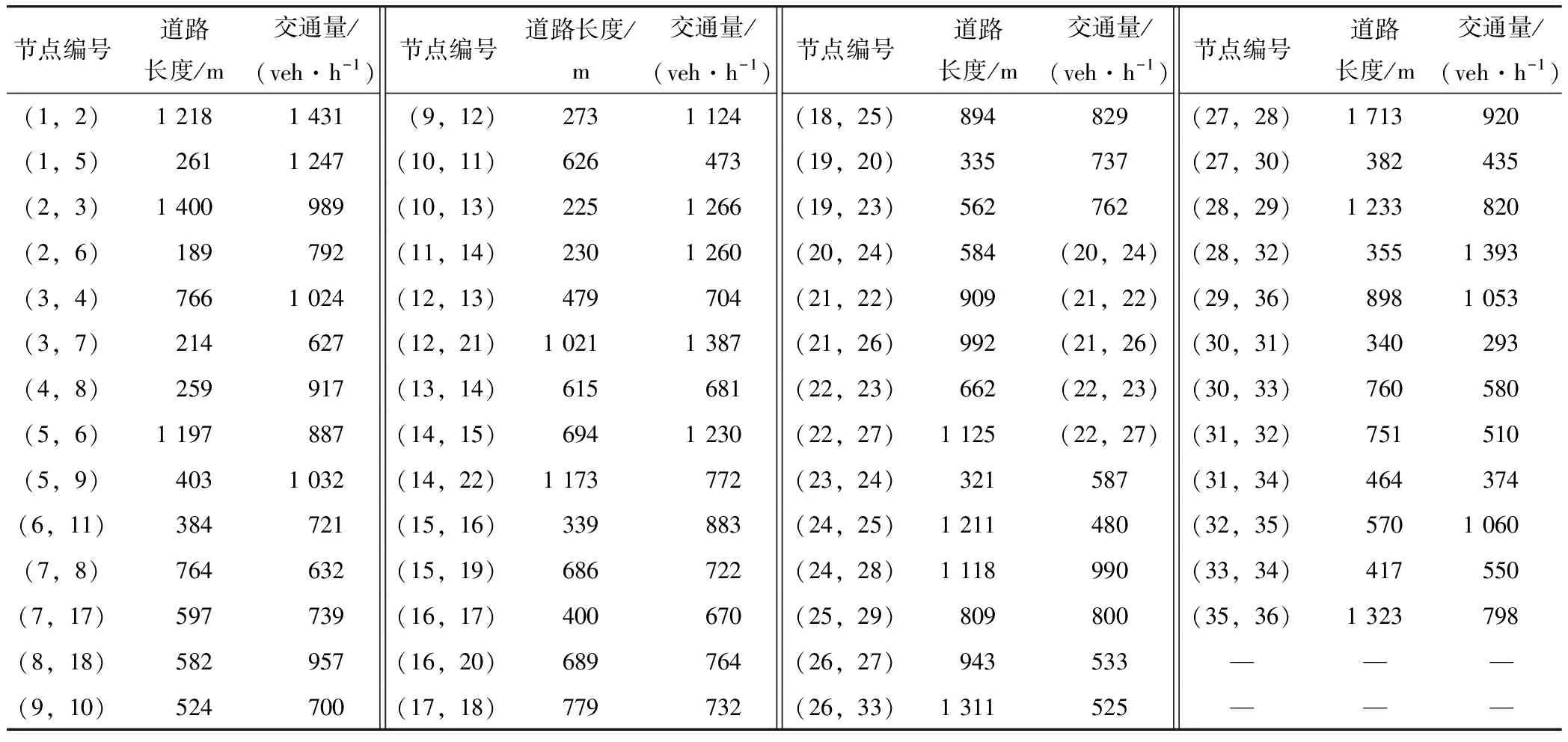
表2 案例路網的相關參數Tab.2 Parameters of road network of case study

(3)應急資源需求信息：根據《突發事件應急管理》中規定的生產安全事故等級標準，判斷該突發性火災的規模屬于較大規模的突發事件。已知該火災發生時消防車輛、救護車輛和警車均需到達現場進行應急救援。查詢應急管理部對火災現場應急處置措施，及較大火災對這3類應急車輛的的需求量，整理得到救援請求點應急車輛的需求量如表3所示。

表3 救援請求點各類應急交通需求分析Tab.3 Analysis of emergency traffic demand at rescue request point

(4)應急車輛調度時間成本：根據公安部相關火災損失統計和損失計算方法[24]，并參考《江蘇省醫療服務項目價格手冊》，計算不同類型應急救援交通的調度時間成本相關參數，如表4所示。同時，結合表2中的相關的路徑長度，計算不同類型應急救援車輛路徑選擇的路段行程時間，結合表4中的行駛費用，最終計算出各類應急救援車輛的調度時間成本。

表4 不同類型應急救援車輛調度成本分析Tab.4 Analysis of scheduling cost of different types of emergency vehicles

(5)調度容量限制成本：通過上述參考文獻，計算每個出救小區出動車輛的固定成本為300元，進而求得不同類型應急救援車輛調度的固定成本；根據應急車輛出動所花費的時間，判斷不同類型應急救援車輛出發的時間間隔為5 min，以此為固定的間隔時間更新路徑交通狀態信息，并計算不同類型應急救援車輛沿線路徑的交叉口處的信號延誤時間。每種應急車輛調度的容量成本情況如表5所示，結合模型可計算應急車輛調度的容量成本。

表5 應急調度車輛的容量限制分析Tab.5 Analysis of capacity limitation of scheduling emergency vehicles

結合上述的雙層規劃的模型參數，進行求解。上層應急車輛的調度為整個雙層規劃模型的主程序，先假設每個出救小區到救援請求點的行駛時間僅考慮最短路徑長度，在迭代完成時，將不同應急出救小區選擇和各類型應急車輛的調度方案導入到下層模型下層根據上層的初始方案進行計算，并考慮到每條路徑的交通狀態，更新路網交通狀態，分別為初始、5 min和10 min的路網交通狀態。

通過計算求得各個出救小區到救援請求點的最優路徑，同時將最優路徑行駛的時間結果返回到上層的調度模型中，上層模型再次調整調度方案，重復迭代此過程，直至得出最終的出救小區選擇、車輛出動數量及路徑優化方案。

求解過程，上層調度的求解中運用 MATLAB編寫相關的應急車輛調度優化函數，運用NSGA-II算法求解，設置遺傳變異算子參數(種群規模50，迭代100次，交叉概率0.8，變異概率0.2)；下層的路徑選擇，根據案例的相關數據，通過MATLAB仿真軟件，運用改進的蟻群算法求解，參數設置為m=200，NCmax=100，α=0.5，β=1，ρ=0.1，最終求解僅考慮調度或路徑優化，以及本研究基于雙層規劃的調度和路徑選擇集成的結果，如圖4所示，雙層規劃模型計算求得的調度成本、行程時間等參數如表6所示。

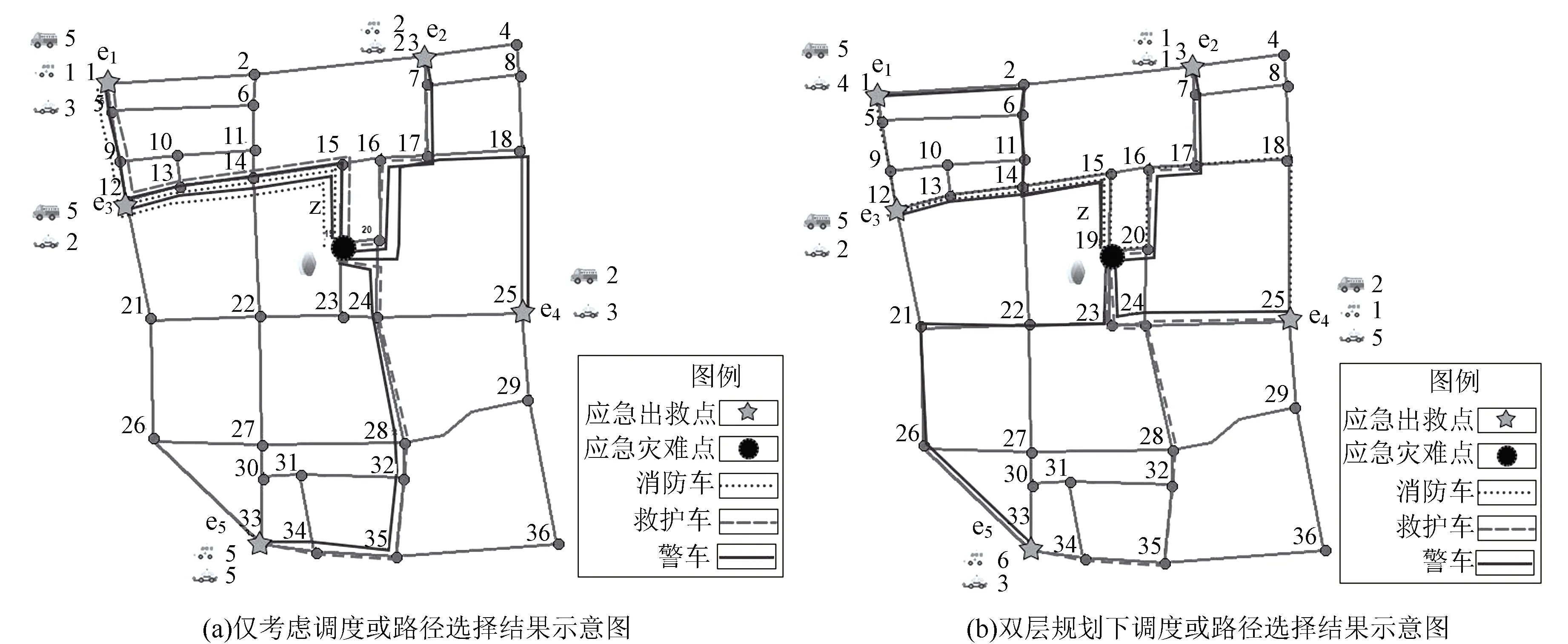
圖4 雙層規劃模型與單獨考慮調度或路徑選擇模型的結果對比Fig.4 Comparison of results of bi-level programming model with models only considering scheduling or route selection

為進一步驗證本研究所采用的雙層規劃模型對基于緊急車輛調度各路徑優化研究的有效性，對僅考慮調度模型中，采用Dijkstra最短路徑分配法對路徑進行選擇；在僅考慮路徑選擇的模型中，采用全有全無分配法對以調度方案進行選擇，最后將3種情況下的費用成本和時間成本進行了對比分析，具體結果如表7所示。

從中可以看出，與僅考慮調度或路徑選擇的應急車輛模型相比，由于雙層規劃模型將調度和路徑優化集成，能夠根據下層道路情況的變化更新最優路徑的選擇，同時反饋給上層調度，更新調度方案，上下兩層相互反饋，可以有效提高應急救援的整體效率，優化資源分配，故上層調度模型總成本降低了2.67%，下層路徑選擇后的在途行程時間減少了21.05%，具體的對比分析示意如圖5所示。此外，與僅考慮調度或路徑優化的模型相比，基于雙層規劃的集成模型克服了重復選取同一條路徑的缺陷，降低路段的壓力，避免擁堵結果的產生。因此，基于雙層規劃的應急車輛優化研究模型所得到的方案要更優越，實用性更高。

5 結論

本研究從不同類型應急救援車輛的調度和動態路徑選擇的集成出發，從調度的固定成本、容量成本和時間成本，以及路徑選擇的路段行程時間和信號延誤時間等多個角度著手，構建了基于雙層規劃模型的不同類型應急車輛調度和路徑選擇集成優化模型，進而采用全局搜索，結合NSGA-II算法和改進蟻群算法對模型進行了求解。最后通過相關的案例，對模型的效果進行了分析對比，結果表明：本研究的集成優化模型與僅考慮調度或路徑選擇的模型相比，在調度成本和路徑選擇的在途行程時間等方面有較好的改進，具有較好的實用性和應用價值。

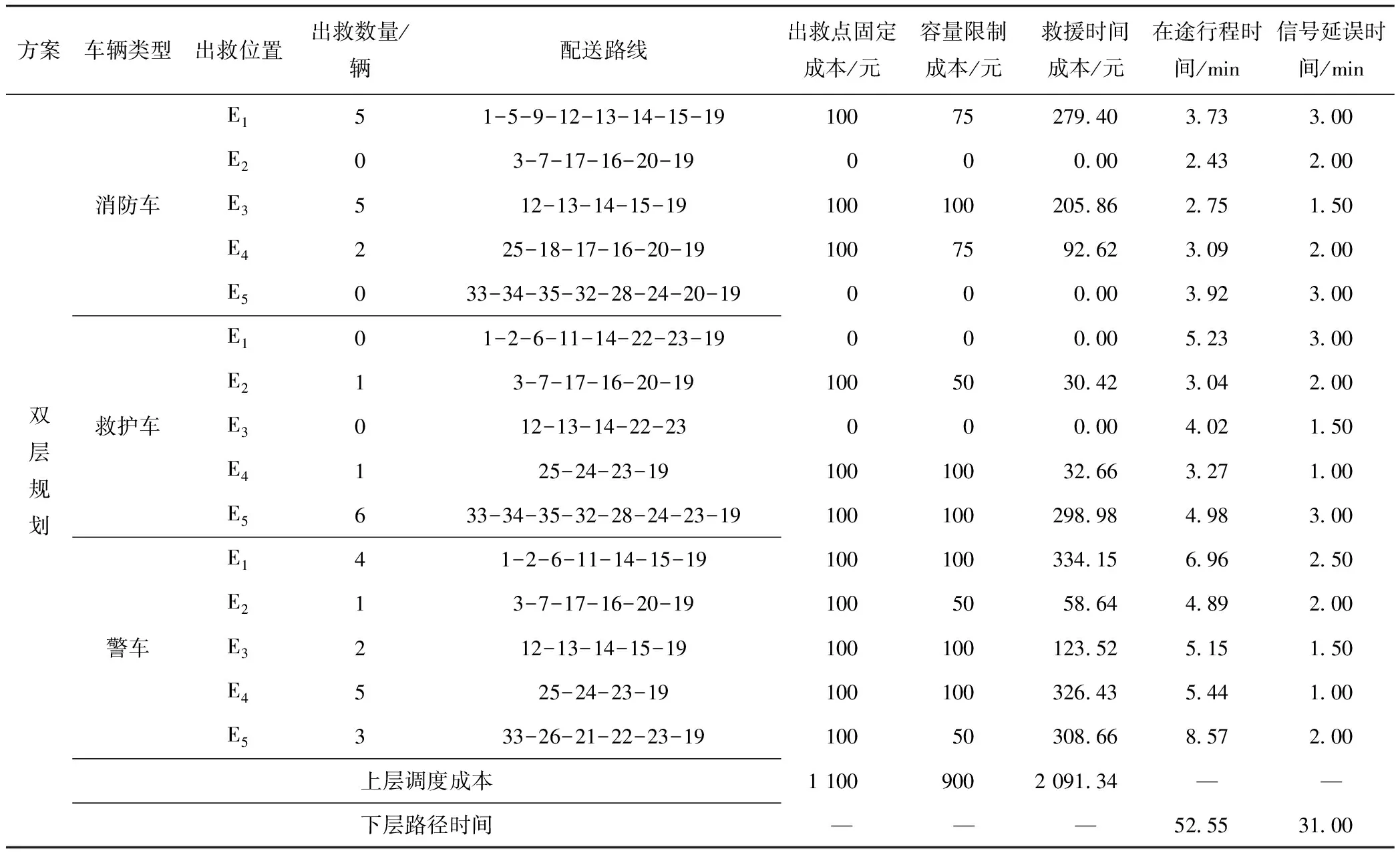
表6 應急救援調度與動態路徑選擇集成的雙層規劃模型結果分析Tab.6 Analysis of result of bi-level programming model of integrated emergency rescue scheduling and dynamic route selection

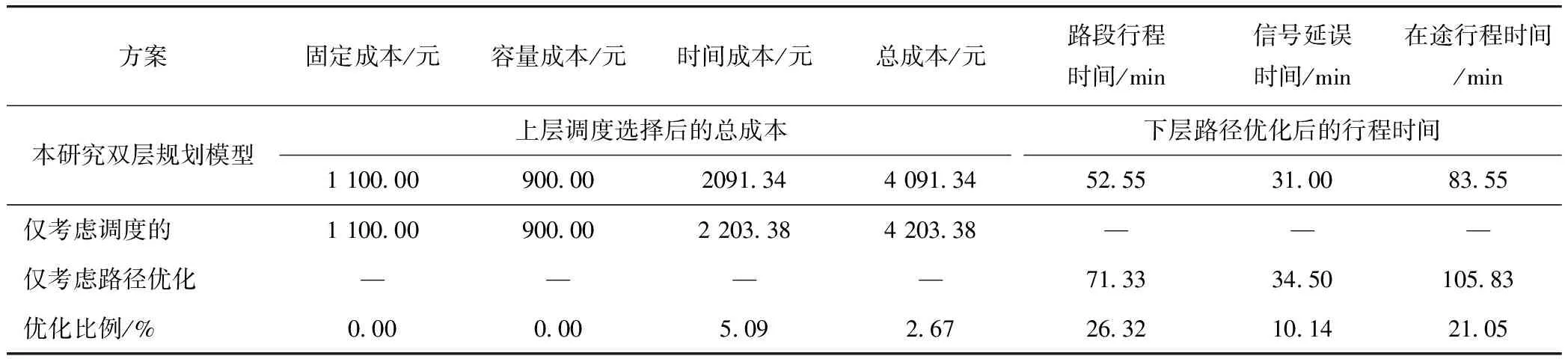
表7 雙層規劃模型與單獨考慮調度或路徑選擇模型的費用時間對比Tab.7 Comparison of costs and time of bi-level programming model with models only considering scheduling or route selection

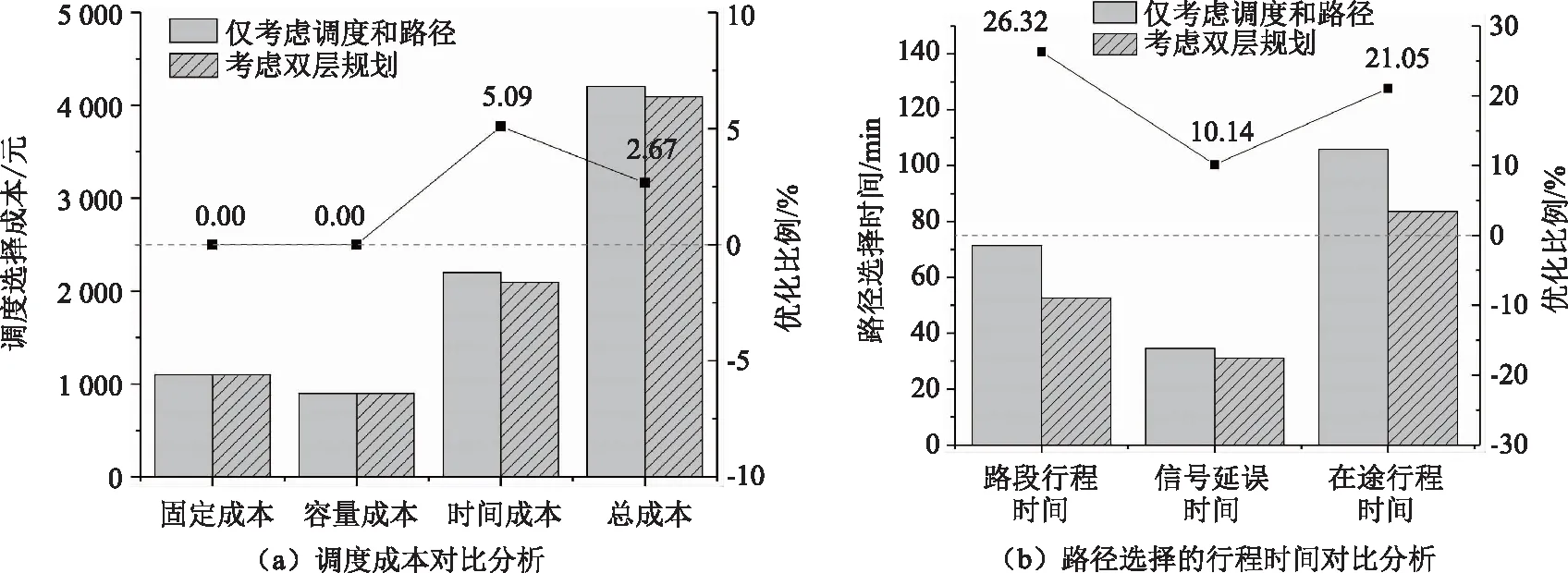
圖5 模型的調度成本和路徑行程時間對比Fig.5 Comparison of scheduling costs and route travel time of models

但應該注意的是，為了簡化運算，研究的案例是基于固定時間的進行路網更新，而現實中路網的變化更為復雜，部分路段的變化情況可能被錯誤預估。因此，面對不同類型應急車輛救援，可在本研究模型的基礎上進一步調整，如針對不同類型車輛的出動優先性也可在后續進一步深入研究。