一種三向等剛度橡膠減振器的研制
趙苗苗,段宇星
(中國飛機強度研究所,陜西 西安 710065)
目前,高速化和大功率化的裝備發展帶來很多有害的振動和沖擊。寬頻隨機振動和大量值沖擊引起結構的共振效應可造成設備的電子配件結構破壞和疲勞失效,嚴重影響裝備的可靠性,從而造成不可預估的結果。
隔振安裝是抑制振動、沖擊和噪聲的有效途徑。減振器能夠將設備與機體隔離,作為抑制設備與機體耦合振動的有效配件,已被廣泛應用于衛星、導彈、艦船、飛機和車輛上的儀器儀表、導航設備和電子系統等上。高阻尼硅橡膠材料因具有寬溫域適用性、高彈性、優良耐候性和長壽命被廣泛應用于航空、航天領域的設備減振降噪和密封等方面[1-3]。
某衛星慣性設備在工作中需要承受19g(g為重力加速度)的振動響應量值及8 000g的沖擊量值,超出了設備的負載能力,嚴重影響其正常使用。本工作基于經典振動理論和橡膠材料的超彈性本構關系,利用有限元分析技術,設計一款兼具緩沖和隔振的橡膠減振器,以解決該慣性設備的振動問題,滿足設計要求。
1 隔振系統簡化模型及橡膠材料本構模型
1.1 經典隔振理論
設備的隔振設計即通過在設備與基礎激勵之間設置柔性連接來衰減兩者之間的能量傳遞和隔離兩者之間的高頻振動。其隔振系統模型可簡化為單自由度隔振模型,如圖1所示。其中,m為設備質量,c為隔振系統阻尼系數,k為隔振系統彈性系數。

圖1 單自由度隔振模型Fig.1 Single freedom degree vibration isolation model
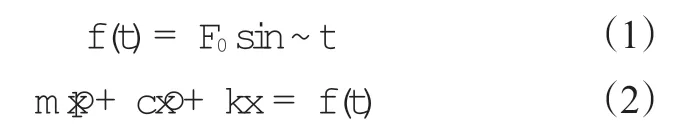
隔振的運動方程[2]為:式中,f(t)為基礎激勵運動函數,F0為無隔振系統時直接作用于設備的力,t為運動時間,ω為隔振系統角頻率。
隔振傳遞系數(Tf)等于隔振安裝環境下作用于設備的力(Ft)與F0的比值:
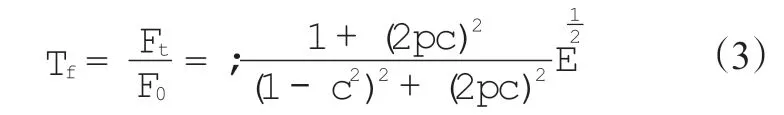
式中,ξ為隔振系統阻尼比,γ為隔振系統振動頻率比,可滿足如下公式
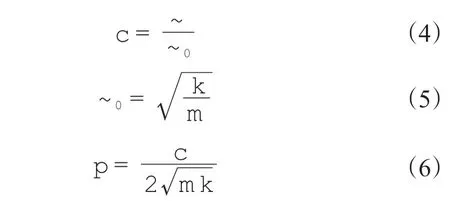
式中,ω0為隔振系統固有角頻率。
Tf的最大值即為振動放大倍數(Q),當ξ比較小時,有
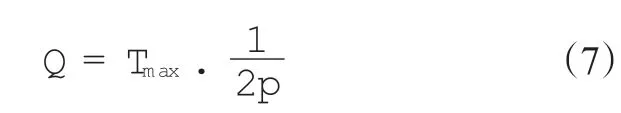
隔振系統的隔振效率(I)為
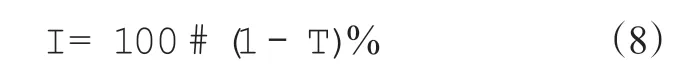
式中,T為Ft在整個頻段的均方根與F0在整個頻段的均方根比值。
當系統激勵頻率(f)大于系統隔振頻率的 2倍時具有隔振效率。系統隔振頻率設計越低,其靜撓度越大,需要的位移空間越大;系統隔振頻率較大時,常達不到需求的隔振效率。一般系統隔振頻率的設計需要考慮實際安裝空間、減振器使用壽命和載荷環境,工程設計中,f一般為系統隔振頻率的2~5倍[3-4]。
1.2 橡膠材料本構模型
橡膠材料是一種各向同性的近似體積不可壓縮的非線性材料,有超彈性特性。橡膠材料在承受不同載荷時表現出非線性,其力學行為與應變率有關。傳統的彈性模量和泊松比已無法表征橡膠材料的本構關系。國內外學者在橡膠材料方面做了大量研究,常見的應變勢能模型有多項式模型、Ogden模型和Arruda-Boyce模型等,在特殊條件下也可以使用簡化的多項式模型,比如Mooney-Rivlin模型、Neo-Hooken模型和Yeoh模型[5-8]。橡膠材料的典型本構模型為多項式模型,其應變能密度(W)表達式[9]如下
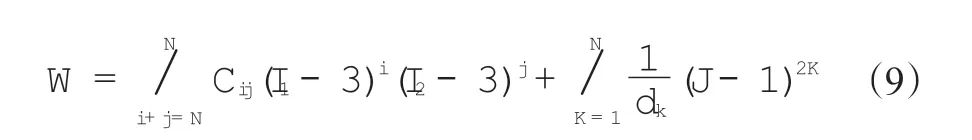
式中:I1和I2分別為第一和第二變形張量不變量;N,Cij,dk描述材料與體積變形無關的部分,根據試驗曲線確定,N,i,j,K為自然數;J為變形后與變形前的體積比,假設材料體積不可壓縮,則J=1。
1.2.1 Mooney-Rivlin模型
對于完全多項式,如果N=1,即可得到Mooney-Rivlin模型,該模型比較適合中小應變情況,其表達式如下
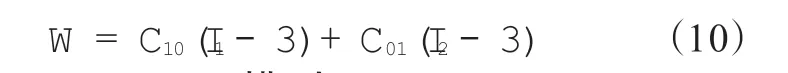
1.2.2 Neo-Hooken模型
對于減縮多項式,如果N=1,即可得到Neo-Hooken模型,其表達式如下
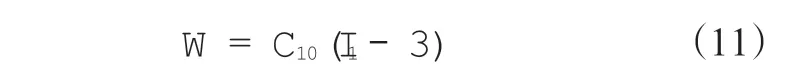
1.2.3 Yeoh 模型
對于減縮多項式,若N=3,即可得到Yeoh模型,其表達式如下
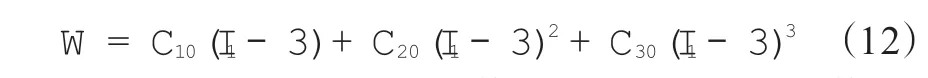
采用Mooney-Rivlin模型、Neo-Hooken模型和Yeoh模型得出的典型橡膠材料應力-應變擬合曲線如圖2所示[10]。橡膠減振器使用中一般控制橡膠材料應變在0~30%。從圖2可以看出,Mooney-Rivllin模型可以準確模擬橡膠材料在小變形下的應力-應變曲線。
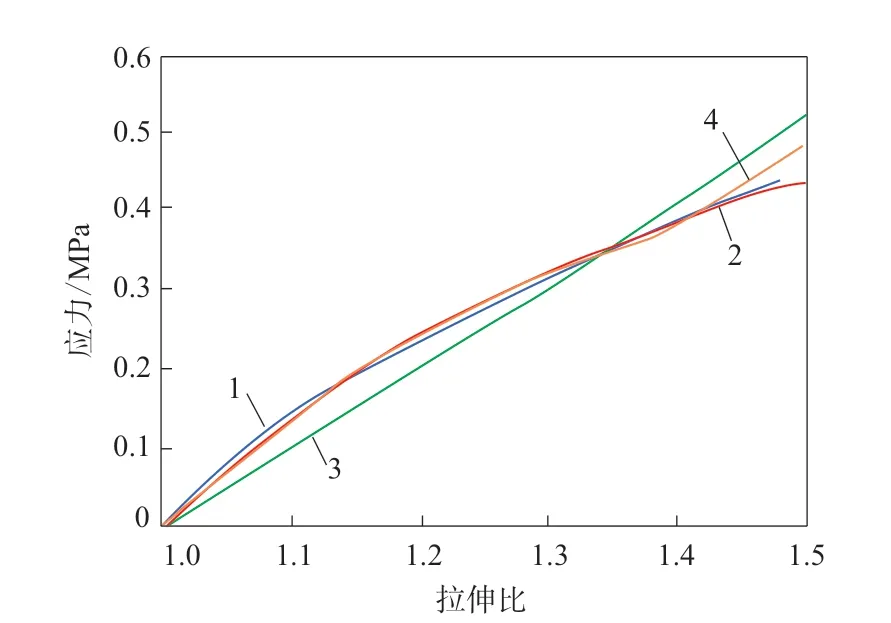
圖2 3種模型得出的典型橡膠材料應力-應變擬合曲線Fig.2 Stress-strain fitting curves of typical rubber material simulated by three models
本工作采用中國飛機強度研究所生產的邵爾A型硬度為30~70度的寬溫域高阻尼硅橡膠材料,將應力-應變數據輸入有限元軟件,經Mooney-Rivlin模型擬合,根據擬合曲線斜率和截距求得硅橡膠材料常數:C10=-0.1,C01=0.35。
2 橡膠減振器設計
2.1 隔振要求
某衛星慣性設備重7 kg,為保證正常使用,設備振動響應量值應由19g降至10g以下,沖擊響應量值應由8 000g降至500g以下。
2.2 隔振理論分析
根據經典隔振理論公式(1)—(8)進行計算,當系統隔振頻率設計為80 Hz時,設備振動響應量值降至10g以下,沖擊響應量值降至500g以下。系統隔振頻率為80 Hz時,安裝橡膠減振器設備的理論振動響應曲線如圖3所示,理論沖擊響應曲線如圖4所示。
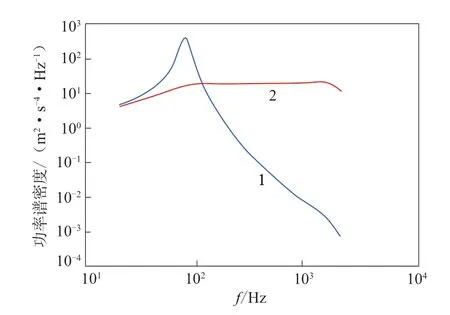
圖3 安裝橡膠減振器設備的理論振動響應曲線Fig.3 Theoretical vibration response curves of equipment with rubber shock absorber
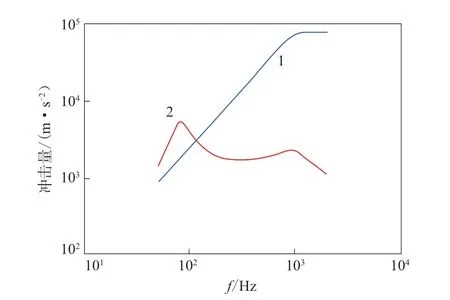
圖4 安裝橡膠減振器設備的理論沖擊響應曲線Fig.4 Theoretical shock response curves of equipment with rubber shock absorber
2.3 橡膠減振器有限元設計
采用商用有限元仿真軟件,選用自研GZ系列橡膠減振器進行改型設計,以系統隔振頻率、橡膠減振器變形量、橡膠減振器安裝結構以及材料參數為約束條件求取最優解。選用Mooney-Rivlin模型為橡膠材料本構關系,金屬材料模量為206 000 MPa,密度為7.8 Mg·m-3,泊松比為0.3;硅橡膠材料密度為1.2 Mg·m-3。經有限元仿真得到橡膠減振器的前3階模態為3個方向的平動,如圖5所示,其中X向振動頻率為77.14 Hz,Y向振動頻率為78.28 Hz,Z向振動頻率為77.97 Hz。從圖5可以看出,橡膠減振器的X,Y,Z3個方向實現等剛度。
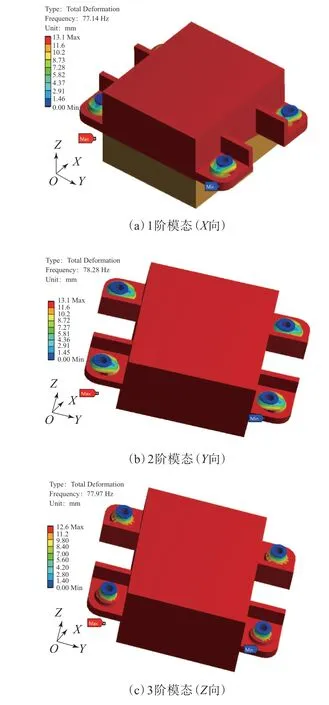
圖5 橡膠減振器振型云圖Fig.5 Vibration mode nephogram of rubber shock absorber
2.4 試驗驗證
依據仿真結果對橡膠減振器進行設計和加工,在振動臺上測試橡膠減振器的振動沖擊性能,實測試驗曲線如圖6和7所示。其中,紅色線為報警線,黃色線為容差線;圖6(a)和(b)中,峰值處f分別為80.4和77.2 Hz。
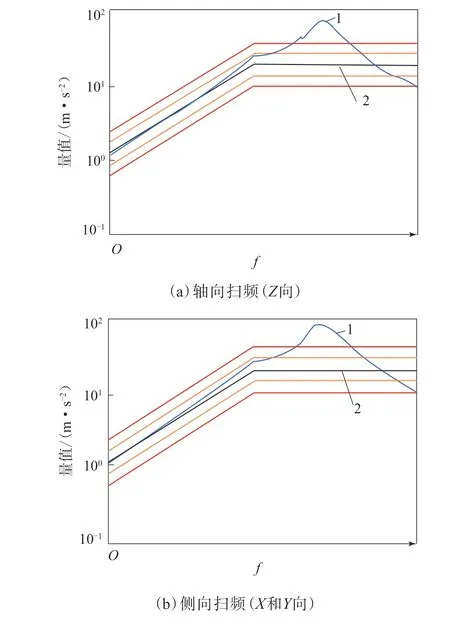
圖6 軸向和側向掃頻結果Fig.6 Axial and lateral sweep results
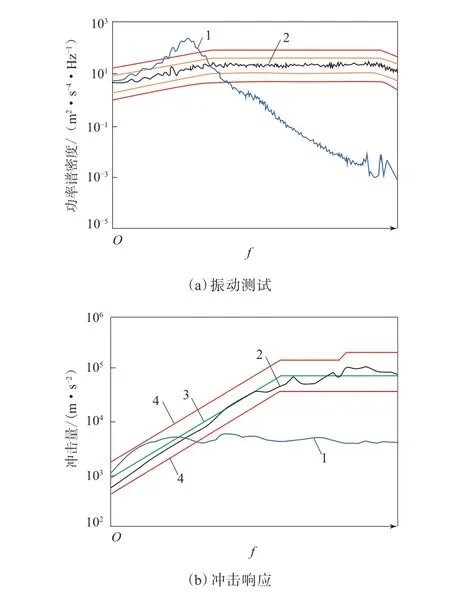
圖7 振動和沖擊響應結果Fig.7 Vibration and shock response results
根據圖6和7計算得出,安裝橡膠減振器后,設備振動量值由19g降至7.7g,沖擊量值由8 000g降至500g,極大地降低了系統的振動、沖擊響應,滿足慣性設備的使用環境要求。
3 結語
采用本研制橡膠減振器對某衛星慣性設備進行隔振緩沖處理,減振效果良好,緩沖效果優異,減少了該設備的振動沖擊問題。

