定向井膠乳水泥石力學適應性有限元評價

劉俊彥，王曉鵬，劉海龍，宋茂林，林家昱，趙軍

1.中海油田服務股份有限公司湛江分公司（廣東 湛江524057）

2.中海石油（中國）有限公司天津分公司（天津300459）

3.中海油田服務股份有限公司（河北 燕郊065201）

水泥環(huán)失效，指水泥環(huán)失去其力學完整性和水力密封性。長期的生產實踐表明[1-3]，在經歷后期套管試壓、射孔、壓裂等作業(yè)以及油氣開發(fā)后，可能會出現(xiàn)由于水泥環(huán)水力密封失效引發(fā)的井口竄流、環(huán)空帶壓等問題，熱采或高溫井下受力更為復雜，水泥環(huán)完整性失效問題也許更為嚴重。究其原因，主要是井內溫壓劇烈變化引起套管-水泥環(huán)-地層系統(tǒng)的變形、應力狀態(tài)發(fā)生改變，導致水泥環(huán)發(fā)生了破壞而喪失水力密封性。國外學者K.Krusche、M.Thiercelin等人[4-6]用解析模型或者實驗方法分析了井下壓力或溫度升高水泥環(huán)的破壞規(guī)律，Gray、W.Wang等人[7-8]采用有限元方法分析了井壁穩(wěn)定性與載荷效應對水泥環(huán)完整性的影響。國內學者房軍、陳朝偉等人[9-10]先后利用彈性力學知識推導出了非均勻地應力條件下組合體受力公式，并對套管和水泥環(huán)受非均勻載荷影響下的強度特性進行了規(guī)律性的分析。但是，針對定向井水泥石在不同溫壓變化條件下的力學完整性研究較少。因此，深入研究固井及后續(xù)各項作業(yè)過程中定向井水泥環(huán)可能發(fā)生的失效形式及其力學機理，對指導定向井水泥石力學性能的合理設計具有重要的意義。

1 控制方程的數(shù)值離散

以環(huán)空水泥環(huán)完全固結之后的套管-水泥環(huán)-地層系統(tǒng)為研究對象。假設套管-水泥環(huán)-地層井周應力坐標變換關系如圖1所示。α為井斜角，（°）；β為井眼方位角，（°）；θ為井周角，（°）；σxx，σyy，σxy，σxz，σyz和σzz為笛卡爾坐標中的井周應力分量，MPa，可以通過地應力坐標轉換計算；R1，R2，R3分別為套管內徑、套管外徑、水泥環(huán)外徑，m；E1，E2和E3分別為套管、水泥環(huán)和地層彈性模量，MPa；μ1，μ2和μ3分別為套管、水泥環(huán)和地層泊松比。1、2、3為地應力的直角坐標系，X1，Y1，Z1為井眼軸線坐標系。

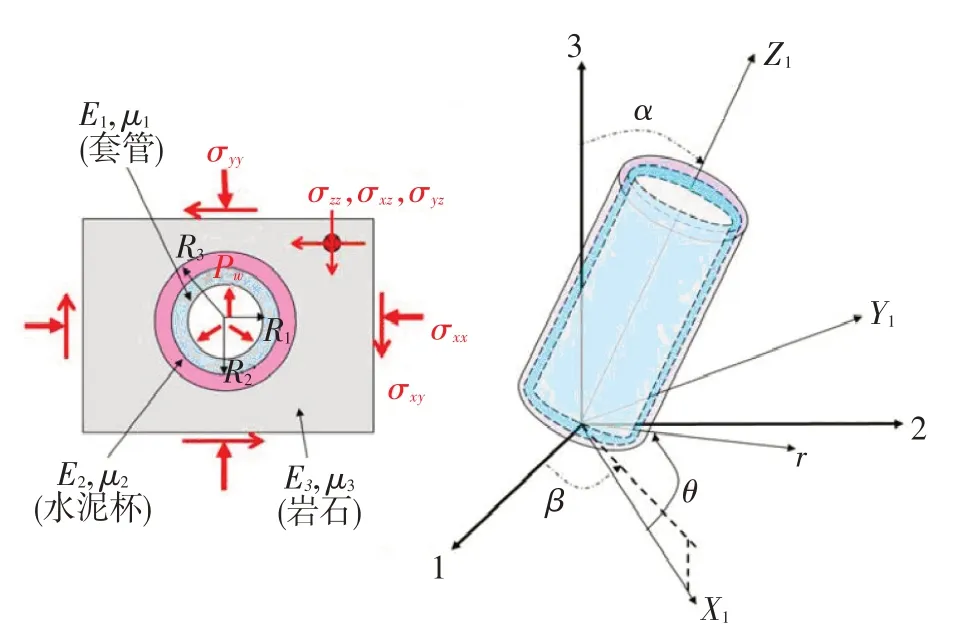
圖1 定向井井軸坐標變換關系

定向井套管-水泥環(huán)-地層井周應力求解過程比較復雜，本文采用有限元方法進行求解分析。在有限元分析中，與微分方程和邊界條件相等價的積分方程，除了用變分原理外，還可以由加權余量法得到。Galerkin加權余量法是建立有限元求解方程的一種有效方法。應用加權余量法直接建立矩陣形式的平衡方程和邊界條件的等效積分方程。

套管-水泥環(huán)-地層系統(tǒng)矩陣形式的平衡方程為：

矩陣形式邊界條件為：

因為σ為位移函數(shù)，故上述兩個方程表示為：

在求解區(qū)域Ω內，權函數(shù)可以不失一般的分別取真實位移的變分δu，在邊界Γσ上取-δu，套管-水泥環(huán)-地層系統(tǒng)平衡方程的等效積分為：

對方程式（5）中的第一項進行分步積分，套管-水泥環(huán)-地層系統(tǒng)的平衡方程和應力邊界條件的等效積分形式為：

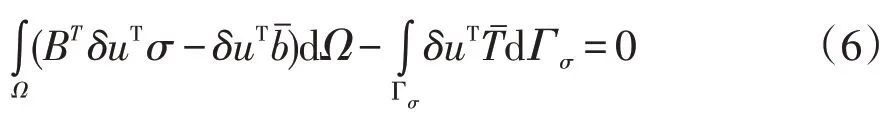
其表述成增量形式為：

將本構方程代入得：

對套管-水泥環(huán)-地層系統(tǒng)的等效積分方程進行空間域上的離散，根據(jù)Galerkin方法，方程中的固相位移u用幾何域上有限個結點的位移表示為：

依據(jù)Galerkin理論，取加權系數(shù)W=N，并取，套管-水泥環(huán)-地層系統(tǒng)的等效積分方程的空間離散方程為：

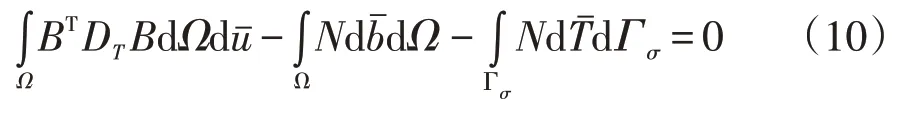
上述方程即為套管-水泥環(huán)-地層系統(tǒng)的有限元計算分析基本方程。

2 水泥環(huán)水力膠結失效的判別準則

在井下載荷作用下，水泥環(huán)的應力狀態(tài)將發(fā)生變化，并且在空間上形成一定的分布規(guī)律，若水泥環(huán)的應力狀態(tài)達到地層的峰值強度時，認為水泥環(huán)發(fā)生了失穩(wěn)。

對于水泥環(huán)來說，受力后可以發(fā)生剪切破壞和拉伸破壞，發(fā)生剪切破壞的判定準則為：

式中：σ1，σ3分別為水泥環(huán)最大和最小主應力，MPa；C為水泥環(huán)的黏聚力，MPa；φ為內摩擦角，°。

水泥環(huán)發(fā)生拉伸破壞的強度準則為：

式中：σt為水泥環(huán)抗拉強度，MPa。

水泥環(huán)完整，但水泥環(huán)與套管或地層的界面發(fā)生破壞，同樣會對水力膠結特性產生影響，因此，必須給出界面安全的判別標準。對于套管-水泥環(huán)界面防止出現(xiàn)剪切滑移的判定標準為：

式中：τ，σn分別為套管-水泥環(huán)界面的剪應力和正應力，MPa；τc-c為套管-水泥環(huán)界面抗剪強度，MPa；fc-c為套管-水泥環(huán)界面摩擦系數(shù)。

對于水泥環(huán)-地層界面防止出現(xiàn)剪切滑移的判定標準為：

式中：τ'，分別為水泥環(huán)-地層界面的剪應力和正應力，MPa；τc-f為水泥環(huán)-地層界面抗剪強度，MPa；fc-f為水泥環(huán)-地層界面摩擦系數(shù)。

除了界面上不能出現(xiàn)拉應力，防止套管-水泥環(huán)界面張開還應滿足的判別條件為：

式中：ur_casing、ur_cement分別為界面上套管和水泥環(huán)的徑向位移，m。

除了界面上不能出現(xiàn)拉應力，水泥環(huán)-地層界面張開還應滿足的判別條件為：

式中：ur_cement，ur_formation分別為界面上水泥環(huán)和地層的徑向位移，m。

3 水泥環(huán)力學性能適應性有限元評價

以海上某油田X井為例，X井地層受正斷層控制，底部地層有異常高壓出現(xiàn)。針對膠乳體系（膠乳加量為18%），建立了定向井套管-水泥環(huán)-地層三維有限元模型，計算了井斜角為90°（水平段）和60°（斜井段）兩種情況，對壓力變化和溫度變化過程中的塑性破壞規(guī)律進行了研究。以該井儲層段為研究對象，地層基本參數(shù)與計算力學參數(shù)見表1。膠乳水泥石力學參數(shù)為：彈性模量為3.7 GPa；泊松比為0.144；黏聚力為6 MPa；內摩擦角為18.3°；熱膨脹系數(shù)為7×10-6℃-1。

表1 X井基本參數(shù)

圖2為該井建立的套管-水泥環(huán)-地層系統(tǒng)三維有限元計算模型，這里做以下規(guī)定：①模型外邊界7 m，厚度0.8 m，固定模型上表面3個腳點自由度，以消除邊界影響；②對模型施加初始地應力場和溫度場；③套管內壁施加均勻壓應力載荷。

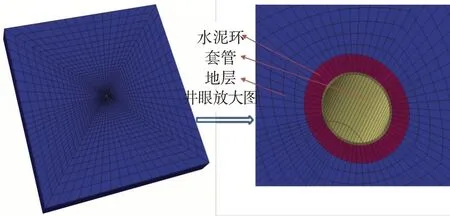
圖2 套管-水泥環(huán)-地層系統(tǒng)有限元三維模型

首先是井斜角為90°時的情況，圖3為膠乳型水泥體系（膠乳加量為18%）分別在13.8 MPa和20.7 MPa試壓條件下的水泥環(huán)塑性破壞程度，可以看出：小試壓條件下采用膠乳型水泥漿形成的水泥環(huán)中未出現(xiàn)塑性區(qū)，水泥環(huán)完好，當套管內壓提高到20.7 MPa時，水泥環(huán)在第一界面最小地應力方位附近出現(xiàn)塑性區(qū)，水泥石發(fā)生剪切破壞，最大等效塑性應變?yōu)?.432×10-3。

圖3 不同試壓條件下水泥環(huán)塑性破壞程度

圖4為膠乳型水泥體系（膠乳加量為18%）分別在60℃、220℃溫度條件下的水泥環(huán)塑性破壞情況，可以看出：對于膠乳型體系來說，溫度從60℃升高到220℃時水泥環(huán)被擠壞，出現(xiàn)了一定的塑性區(qū)，最大等效塑性應變?yōu)?.196×10-4。

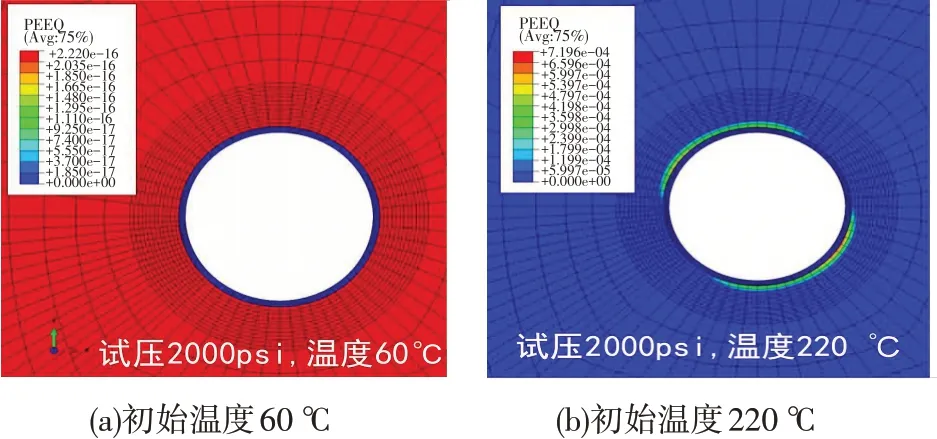
圖4 不同溫度條件下塑性破壞情況

改變井斜角為60°（井斜段），圖5為膠乳型水泥體系（膠乳加量為18%）分別在不同溫度條件下的水泥環(huán)塑性破壞，可以看出：在同樣的溫度和試壓條件下，井斜角由90°變?yōu)?0°時，水泥環(huán)等效塑性應變明顯降低，最大等效塑性應變?yōu)?.528×10-4。而溫度為60℃時，水泥環(huán)還未進入塑性，說明對于該區(qū)塊地應力一致的情況下，斜井段水泥環(huán)抗溫變能力比水平段強。

圖5 改變?yōu)?0°井斜條件下的塑性破壞

4 結論

1）有限元計算結果表明，隨著試壓壓力增加，塑性區(qū)在不斷增加，等效塑性應變逐漸增加，膠乳水泥石試壓值不超過20.7 MPa。

2）隨著溫度增加，塑性區(qū)在不斷增加，等效塑性應變逐漸增加，膠乳水泥石抗高溫值不超過220℃。

3）斜井段比水平段中的水泥環(huán)進入塑性的風險要小一些。

4）不同的水泥配方，不同的目標地層，臨界試壓和溫度值是不相同的，所以合理的水泥環(huán)力學參數(shù)選取應該綜合考慮套管-水泥環(huán)-地層系統(tǒng)的力學參數(shù)匹配性和以及該系統(tǒng)所承受的內壓和原始地應力相對關系。