激振和循環加載下浮置板軌道動力參數試驗研究
汪楊鑫 練松良 朱錦澤 陳高峰
(1. 同濟大學道路與交通工程教育部重點實驗室, 201804, 上海;2. 上海市軌道交通結構耐久與系統安全重點實驗室, 201804, 上海;3. 隔而固振動控制有限公司技術中心, 266108, 青島∥第一作者, 碩士研究生)
軌道結構動力參數測試是測試軌道結構受到外界激勵時軌道部件的力、位移、速度、加速度等動力學參數的試驗[1]。目前對浮置板的動力測試有落軸法、落錘法、錘擊法、循環荷載法等試驗方法。這些方法在鐵路領域研究中已有應用[2-4]。在城市軌道交通領域,文獻[5]建立了浮置板有限元模型,將隔振器視為彈簧振動;文獻[6]建立了車輛-浮置板耦合模型,給出了隔振器阻尼的適宜范圍;文獻[7]給出了隔振器阻尼比的計算方法;文獻[8]驗證了循環加載求解浮置板阻尼比的準確性。
試驗方法的不同,試驗的難度、成本、適用性也各不相同。本文分別對浮置板軌道施加激振和循環荷載,根據動力學理論對鋼彈簧浮置板的剛度、自振頻率和阻尼比等參數進行分析,對比研究不同試驗方法的準確性和適用范圍,為不同條件下選擇合適的試驗方法提供依據。
1 激振加載
落軸試驗是將1 000 kg左右輪對吊起10~30 mm的高度,讓其自由落體沖擊鋼軌。該試驗一般適用于對整板軌道結構的測試,對單個隔振器的測試并不適用。在每個測試高度均需要實施落軸5次以上的試驗,且每次落軸時2個輪對接觸鋼軌的時間差應小于0.03 s,試驗數據方可視為有效。
落錘試驗是將50 kg質量錘以100~500 mm的高度沖擊鋼軌,使系統激振。落錘也可沖擊混凝土道床或用于單個扣件的振動響應對比試驗。沖擊混凝土時需要在沖擊點上粘1塊鋼板,以免砸碎混凝土。
錘擊試驗是使用5.5 kg的普通鐵錘或測力錘進行錘擊。對于整板測試,既可錘擊浮置板,也可錘擊鋼軌。若錘擊鋼軌,則需要考慮鋼軌扣件的彈性作用。
激振加載時,對浮置板施加激振力P,隔振器可視為圖1 b)所示的單自由度振動系統,其動力方程為:
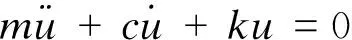
(1)
式中:
m——浮置板質量;
u——浮置板位移;
c——隔振器阻尼;
k——隔振器剛度。
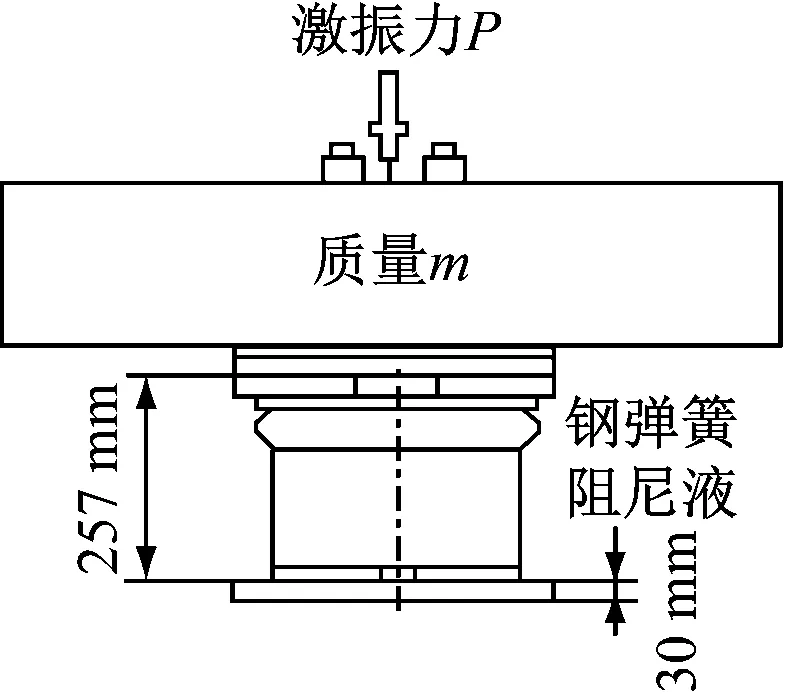
a) 隔振器實體
設u(t)為位移函數,令:
u(t)=est
(2)
(3)
(4)
式中:
t——振動時間;
s1,2——解的2個虛根。
ζ——低阻尼體系阻尼比;
ωn——無阻尼體系自振頻率;
ωD——阻尼體系自振頻率。
將式(2)~(4)代入式(1),得到自由振動解:
(5)
由相鄰振動峰值之比可得到ζ。為了提高精度,ζ可由多個峰值得出:
(6)
式中:
λ——單個波形對數衰減率;
n——自由振動波形個數;
Xi——第i個波峰的位移幅值,mm;
Xi+n——第i+n個波峰的位移幅值,mm。
2 循環(疲勞)加載
加載頻率為3~5 Hz,1個車輛轉向架的荷載為320 kN,考慮動載系數,取最大荷載為360~380 kN;為防止最小荷載為零時試驗裝置起跳,設最小荷載為30~50 kN。
循環加載由于結構中存在阻尼,使得加載和卸載的荷載位移曲線不是同一路徑,由此產生滯回曲線。由滯回曲線最高點和最低點可以得到浮置板的動剛度K的計算式為:
(7)
式中:
P1——滯回曲線最高點的荷載;
P2——滯回曲線最低點的荷載;
y1——滯回曲線最高點的位移;
y2——滯回曲線最低點的位移。
等效阻尼力在1個循環內所做的功等于滯回曲線所包圍的面積,其計算式為:
(8)
式中:
ED——等效阻尼力所做功,J;
ω——振動頻率,Hz;
u0——最大位移,mm。
由此可求得阻尼比為:
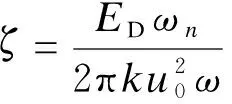
(9)
3 動力參數計算
3.1 剛度
工程中一般采用逐級靜態加載法得到靜剛度,用循環加載法得到整板試驗的低頻動剛度。
逐級加載的荷載范圍為0~180 kN,加載級差為30 kN,共進行3次實施加載試驗,6個位移測點的具體位置如圖2所示,1#測點與3#測點、4#測點與6#測點以板的中線上下對稱分布。

圖2 逐級加載試驗的位移測點布置圖
由于荷載和位移成近似線性增大的關系,因而各測點上各次加載試驗產生的位移值近似,故取算術平均值用于剛度計算,得到各測點的荷載-位移曲線如圖3所示,各測點的平均割線剛度如圖4所示。
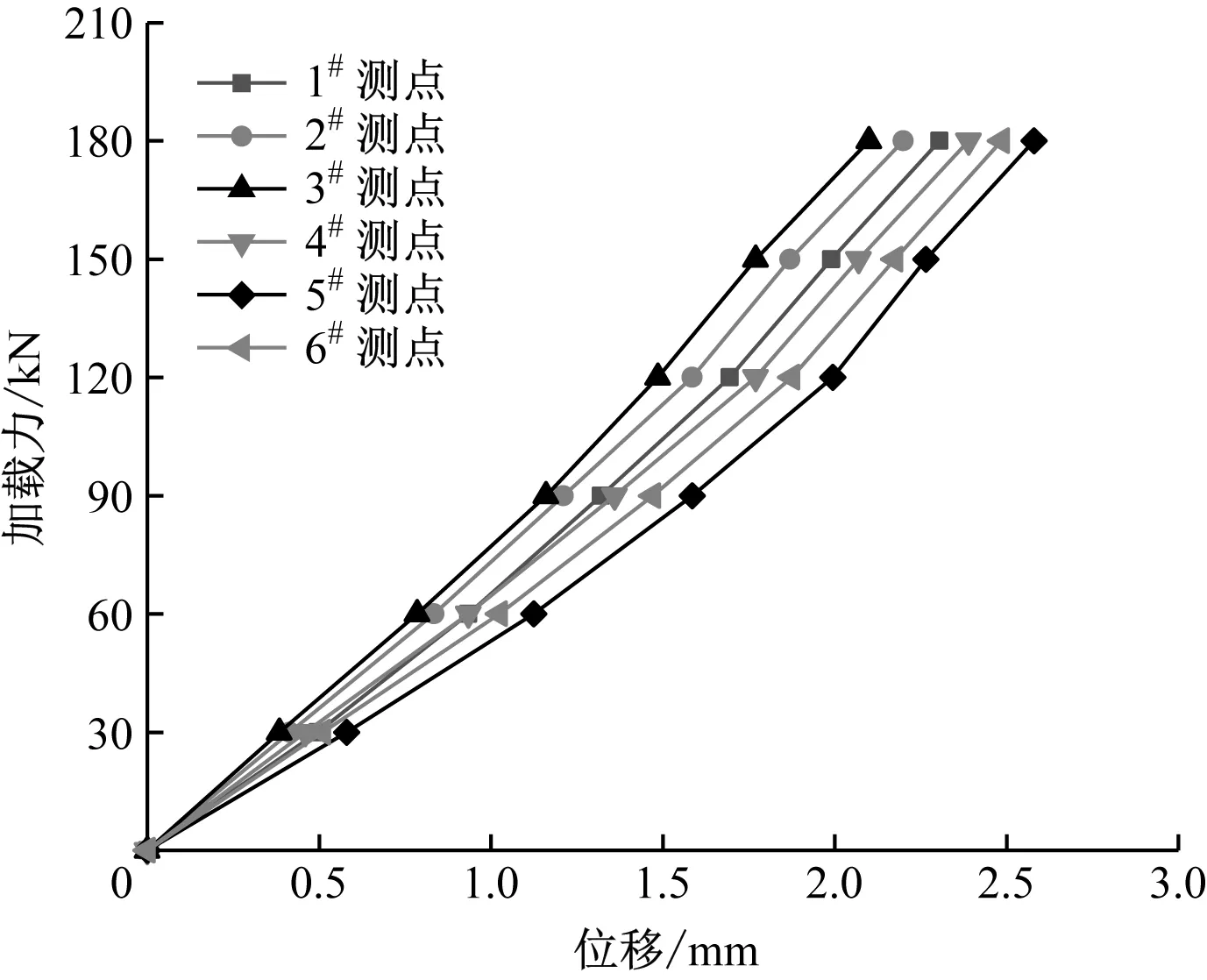
圖3 逐級加載各測點的位移-剛度曲線
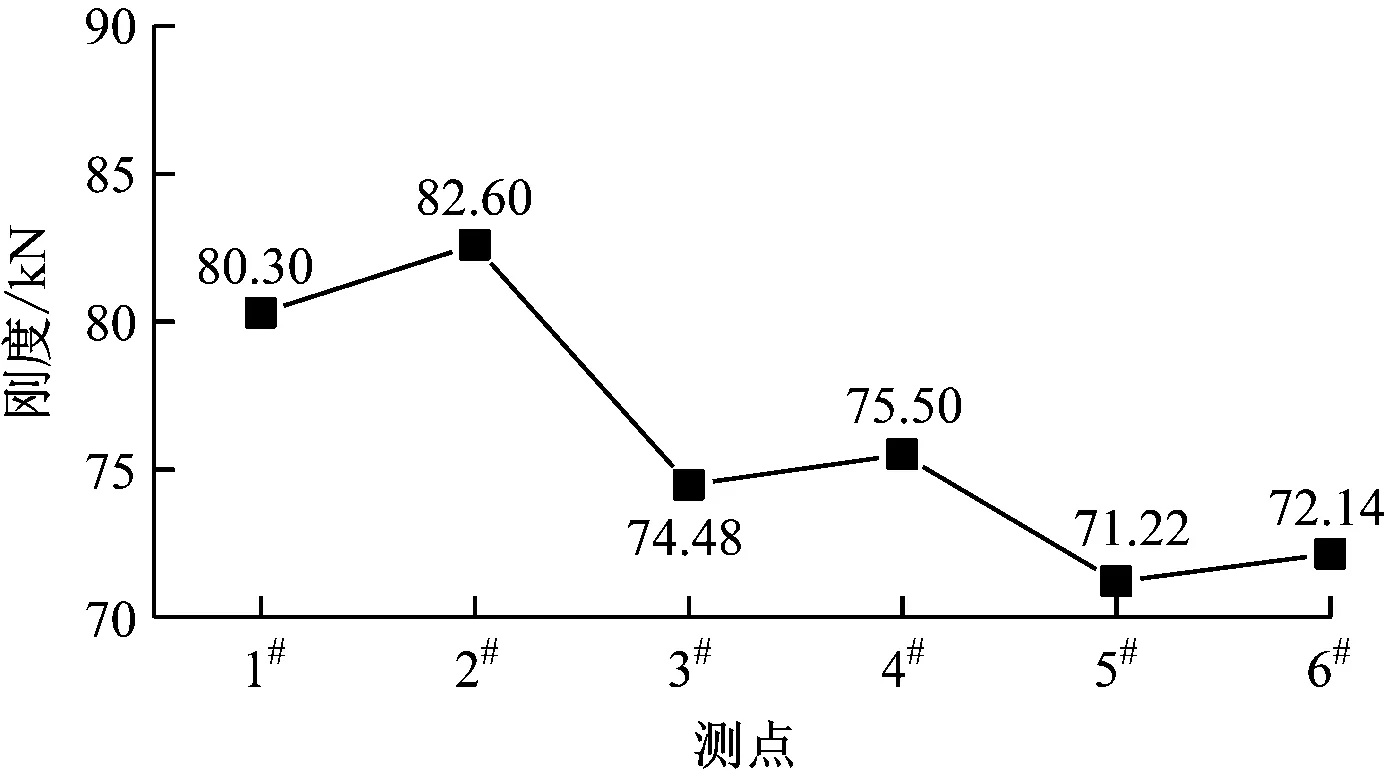
圖4 逐級加載各測點的剛度
低頻加載動剛度測試中,加載次數從0次到第500萬次的滯回曲線如圖5所示。各滯回曲線的圖形沒有顯著差異,可見循環加載產生的疲勞破壞沒有對浮置板的動力性能產生顯著影響。計算得到不同疲勞次數的動剛度如圖6所示。
由上述結果可進一步得到,該浮置板整板的平均靜剛度為75.66 kN/mm,平均動剛度為78.06 kN/mm,動靜剛度比為1.03。試驗結果滿足CJJ/T191—2012《浮置板軌道技術規范》第4.4.4條“單個隔振器的動靜剛度比小于1.3”的要求。
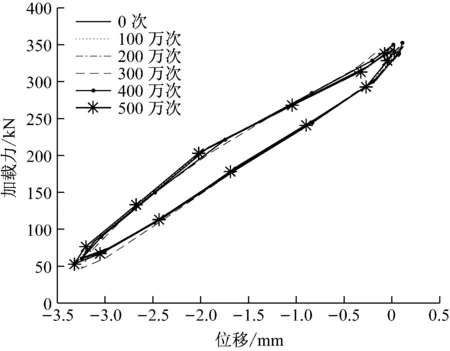
圖5 低頻加載動剛度測試滯回曲線
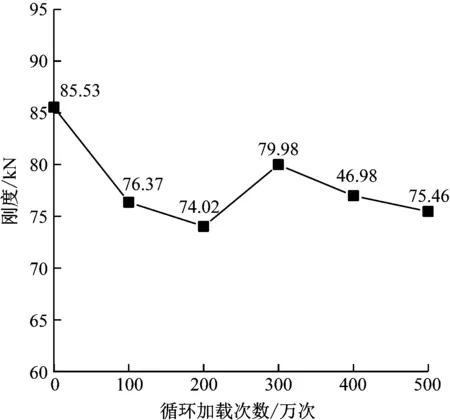
圖6 不同循環加載次數下的動剛度
3.2 自振頻率
激振加載測得的位移-時間曲線如圖7所示。錘擊和落軸引起的浮置板位移數值變化差異較大,但20 mm落軸、10 mm落軸、捶擊三種情況下得到的位移-時間曲線波形類似,均較好地反映出浮置板的自由振動特征。

a) 三種情況
激振加載測得的振動加速度-時間曲線如圖8。落軸和錘擊產生的加速度值在量級上基本一致,差別在±20 m/s2范圍內。落軸波形較錘擊波形雜亂,這是由于輪軸沖擊鋼軌后多次起跳導致。
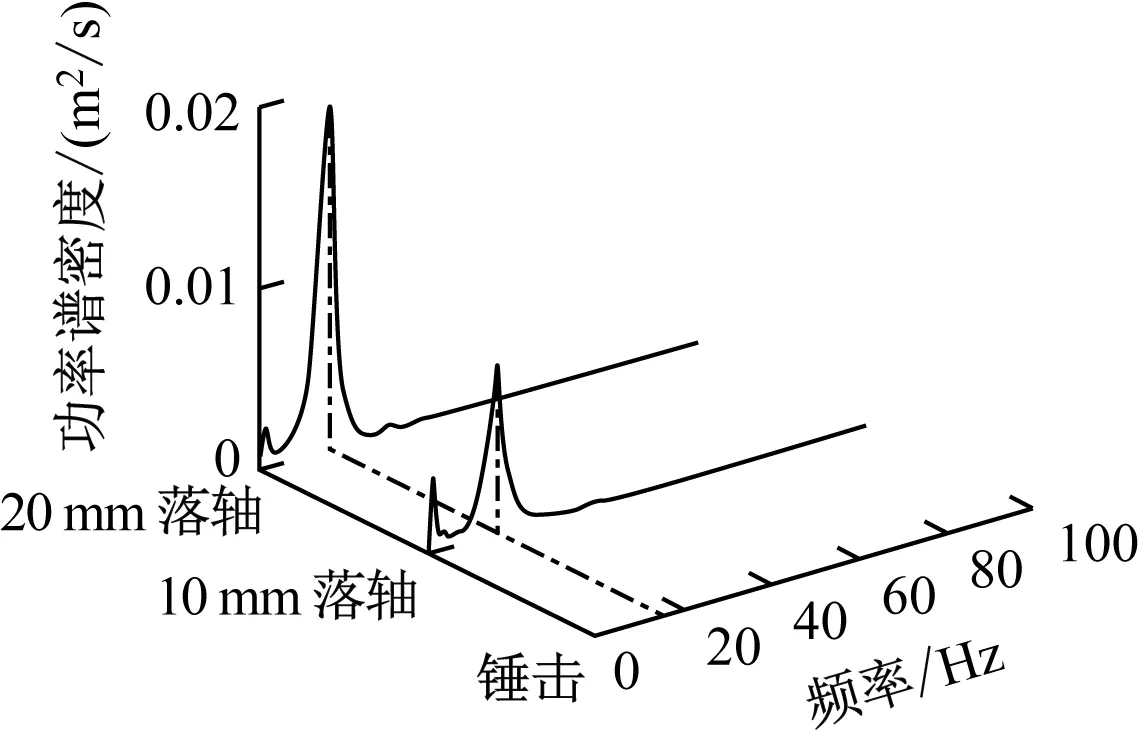
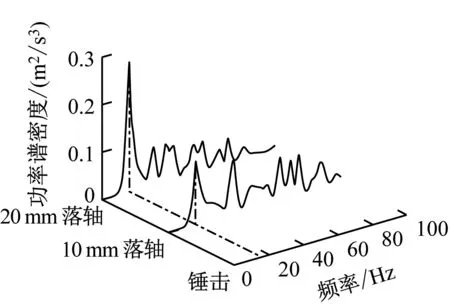
不同的激振荷載下浮置板的位移功率譜密度如圖9所示,加速度功率譜密度如圖10所示。由圖9~10可以看出,錘擊和落軸的功率譜密度函數均在15.870 Hz出現最大峰值,因而可以得到該浮置板的自振頻率為15.870 Hz。
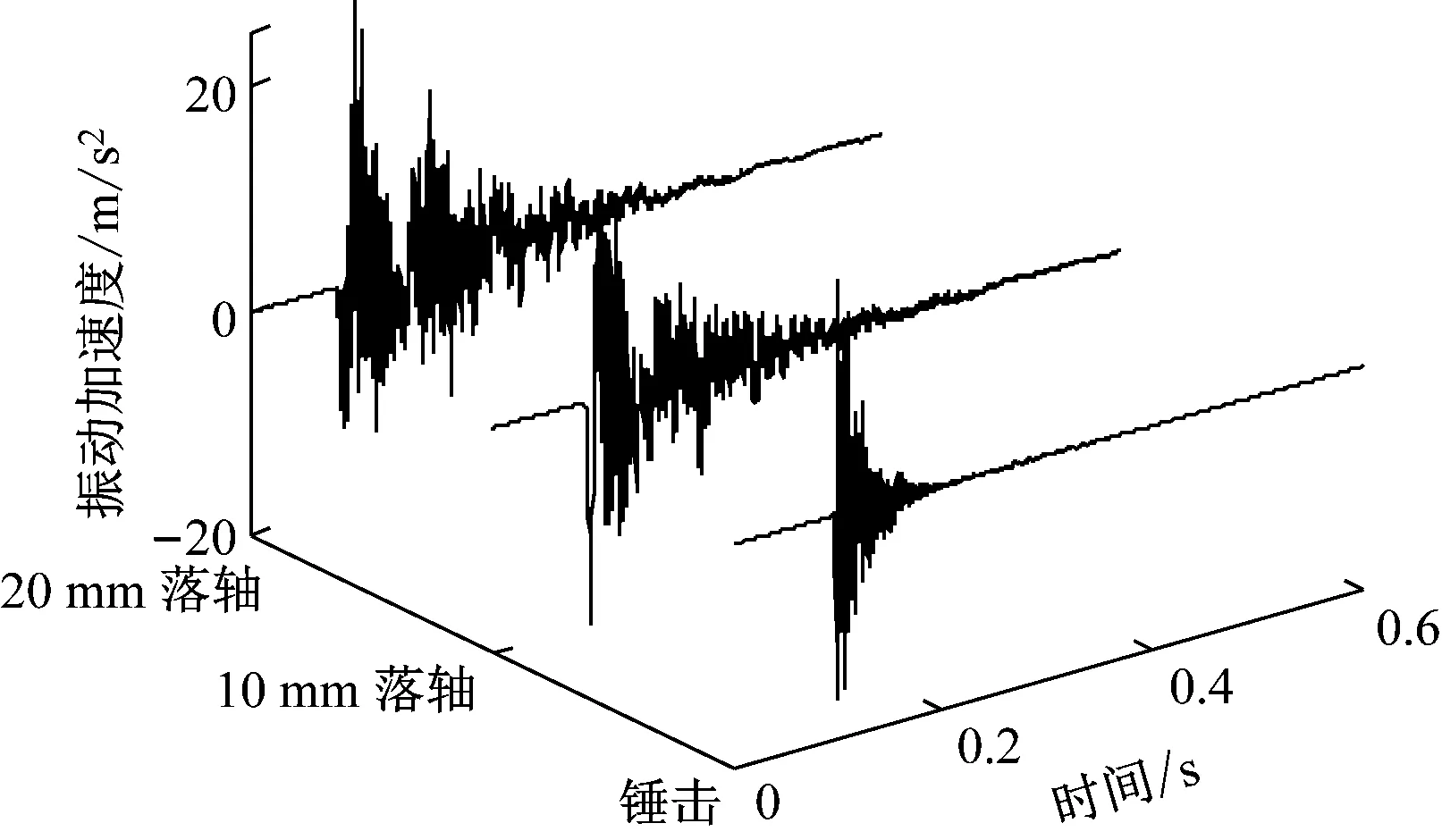
圖8 激振荷載下的振動加速度-時間曲線
a) 三種情況
a) 三種情況
如圖9所示,對于位移功率譜,激振力越大,主頻處的峰值越大。除去主頻的15.870 Hz,錘擊時在1.221 Hz、4.883 Hz處存在尖峰,落軸時在1.221 Hz處存在尖峰。1.221 Hz、4.883 Hz這些非主頻處尖峰可能是由于浮置板側傾振動和撓曲振動所致。如圖10所示,對于加速度功率譜,仍可得到類似結論,但由于加速度功率譜放大了高頻的成分,可以看到在大于主頻的頻率上還有數個尖峰出現。
該試驗的浮置板質量約為10 530 kg。逐級加載測得的剛度為75.66 kN/mm,可求得此時的自振頻率為13.490 Hz;低頻3~5 Hz循環加載的動剛度為78.06 kN/mm,可求得此時的自振頻率13.710 Hz。這2個數據與上文求出的15.870 Hz不完全一致,其主要原因是在整板試驗時沖擊是高頻荷載,浮置板所表現出來的剛度不是靜剛度和低頻動剛度,而是高頻動剛度,故沖擊試驗時測得浮置板的整板振動主頻要大于理論計算的自振頻率。
3.3 阻尼比
浮置板阻尼比的測試采用基于激振的對數衰減率法和基于循環的滯回曲線法。為了排除浮置板其他階振型和其他噪聲信號產生的影響,試驗時以浮置板的自振頻率為中心頻率進行帶通濾波,濾波前后的波形如圖11所示。
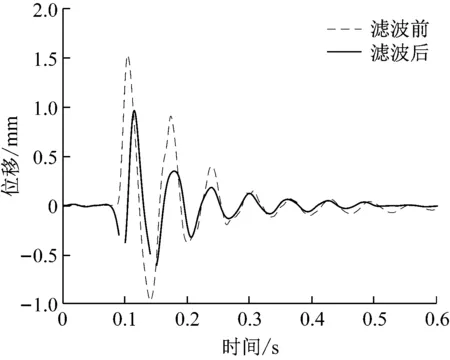
圖11 濾波前后位移波形對比
分別選取10次錘擊力在10~20 kN的錘擊數據,以及落軸高度分別為10 mm和20 mm各5次的有效落軸數據,在式(6)計算時,n分別取1~6。錘擊和落軸求得的平均阻尼比隨相鄰振動峰值數變化的趨勢如圖12所示。從圖12可見,不同的激振方式測得的阻尼比沒有顯著差別,隨著相鄰振動峰值數的增加,阻尼比總體呈下降趨勢。這是由于位移衰減波的前幾個尖峰的振動衰減率大于后幾個尖峰的振動衰減率,也說明了目前的隔振器阻尼比與位移并非線性相關。當相鄰振動峰值數取3或4時,阻尼比取值穩定,說明在運用激振荷載測試阻尼比時應選取相鄰3~4個峰值進行計算較合理。

圖12 激振荷載下不同相鄰振動峰值數的阻尼比
對于循環加載,選取每100萬次加載次數的典型滯回曲線進行計算,得到阻尼比如圖13所示。由圖13可知,阻尼比最大值為加載200萬次和400萬次時的0.127,最小值為0次時的0.120,各阻尼比之間數值較為接近。

圖13 不同循環加載次數下的阻尼比
錘擊、落軸試驗時隔3個周期計算阻尼比,計算循環測試下各加載次數的平均阻尼比,其結果如圖14所示。由圖14可知,不同試驗方法測得的阻尼比數值比較接近,最小值和最大值相差11.9%,可以滿足工程計算要求,說明激振和循環加載均能較準確地測得鋼彈簧浮置板的阻尼比。
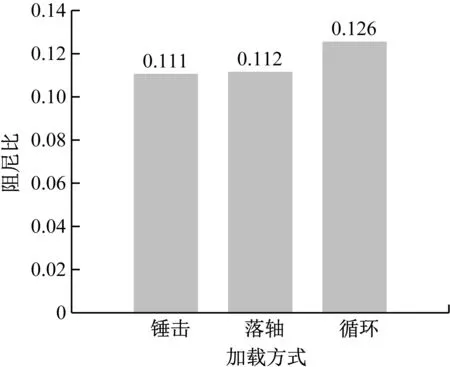
圖14 不同試驗方法測得的阻尼比
4 適用性比較
綜合以上對動力參數的試驗研究,結合工程應用實際,整理得到不同試驗的適用性,如表1所示。在實際測試中,應結合測試目的、測試條件等選用合適的測試方法。

表1 激振和循環加載試驗適用性
5 結論
1) 對于鋼彈簧浮置板的剛度,逐級加載法測得的靜剛度數值和循環加載利用滯回曲線測得的動剛度數值接近。在浮置板未發生疲勞破壞時,這2種方法測得的剛度沒有顯著區別。
2) 錘擊和落軸的激振荷載作用下,可以準確地求得浮置板的自振頻率。激振荷載越大,自振頻率的峰值能量越集中。在現場測試時,可以用較簡便的錘擊試驗代替落軸試驗來求取自振頻率,但是錘擊試驗各頻率峰值較多,在選取時應格外注意,可結合位移功率譜和振動加速度功率譜綜合考慮。
3) 激振加載計算阻尼比之前,需要根據鋼彈簧浮置板的自振頻率進行濾波處理。激振力大小對阻尼比計算結果沒有顯著影響。疲勞加載運用滯回曲線計算得到的阻尼比和激振加載計算得到的阻尼比沒有顯著區別。運用這2種加載方式均可以較準確地計算得到阻尼比。

