FLNG丙烷預(yù)冷雙氮膨脹液化工藝中試裝置試驗(yàn)分析*
李恩道 尹全森 劉淼兒 陳 杰 張樹勛
(中海石油氣電集團(tuán)有限責(zé)任公司 北京 100028)
FLNG丙烷預(yù)冷雙氮膨脹液化工藝中試裝置試驗(yàn)分析*
李恩道 尹全森 劉淼兒 陳 杰 張樹勛
(中海石油氣電集團(tuán)有限責(zé)任公司 北京 100028)
為驗(yàn)證中國海油自主研發(fā)的丙烷預(yù)冷雙氮膨脹新型FLNG液化工藝的技術(shù)可行性及適應(yīng)性,建設(shè)了一套2萬m3/d規(guī)模的液化中試裝置。通過試驗(yàn)驗(yàn)證了冷卻溫度、天然氣壓力對(duì)液化工藝的影響,并進(jìn)行了液化單元快速開停車方案試驗(yàn)。試驗(yàn)結(jié)果表明:隨著混合冷劑級(jí)間冷卻溫度降低,F(xiàn)LNG液化中試裝置液化能耗降低,試驗(yàn)過程中冷卻溫度降低12 ℃條件下天然氣處理能力增加4.26%,液化單位能耗減少約5%;FLNG液化中試裝置快速開車時(shí)間主要受板翅式換熱器的降溫速度要求限制,先開啟過冷氮?dú)庋h(huán),再開啟液化段氮?dú)庋h(huán)是達(dá)產(chǎn)最快的開車程序,開車5 h內(nèi)可以達(dá)到設(shè)計(jì)生產(chǎn)負(fù)荷;FLNG液化中試裝置具有快速停車性能,可以在5 min內(nèi)關(guān)停,停車后5 d內(nèi)冷箱恢復(fù)常溫;隨著天然氣壓力降低,F(xiàn)LNG液化中試裝置液化能力下降,試驗(yàn)過程中天然氣壓力從3 547 kPa降低到2 000 kPa時(shí)天然氣處理能力降低11.2%。本文試驗(yàn)分析結(jié)果為大型FLNG液化裝置工程化提供有效技術(shù)保障。
FLNG;丙烷預(yù)冷雙氮膨脹;液化工藝;中試裝置;試驗(yàn)分析
浮式液化天然氣(FLNG)裝置以其投資相對(duì)較低、產(chǎn)能建設(shè)周期短、便于遷移和LNG市場(chǎng)靈活等優(yōu)點(diǎn)越來越受到重視和關(guān)注[1-2]。我國FLNG裝置研究起步較晚,“十一五”期間開始FLNG關(guān)鍵技術(shù)的研究,經(jīng)過近10年的發(fā)展已經(jīng)初步具備了深入研發(fā)FLNG裝置的條件[3]。天然氣液化是浮式LNG裝置的關(guān)鍵,直接影響到整個(gè)裝置運(yùn)行的合理性和適用性[4]。經(jīng)過國家科技重大專項(xiàng)的技術(shù)研究,針對(duì)我國南海惡劣的海況條件,已研發(fā)出一種針對(duì)海上大中型天然氣田的新型FLNG液化工藝——丙烷預(yù)冷雙氮膨脹液化工藝[5],液化工藝中氮?dú)庵评鋭┦冀K處于氣相,幾乎不受船體運(yùn)動(dòng)的影響,且氮膨脹流程與使用易燃制冷劑技術(shù)的流程相比更加安全,但氮膨脹制冷液化工藝流程的制冷劑循環(huán)量大、效率低,僅適用于海況惡劣、天然氣液化處理量小的情況[6],為此在液化工藝中增加了丙烷預(yù)冷循環(huán),提高了裝置的處理能力,并且效率上也有了進(jìn)一步提升。為了驗(yàn)證這套自主研發(fā)的新型FLNG液化工藝的技術(shù)可行性及適應(yīng)性,建設(shè)了一套2萬m3/d規(guī)模的FLNG液化中試裝置,進(jìn)行了環(huán)境適應(yīng)性及部分負(fù)荷工況等試驗(yàn),為大型FLNG液化裝置的工程化提供了有效技術(shù)保障。
1 新型FLNG液化中試裝置工藝流程
規(guī)模達(dá)240萬t/a的新型FLNG液化工藝流程分為3個(gè)制冷循環(huán),分別是丙烷預(yù)冷循環(huán)、液化段氮?dú)庋h(huán)和過冷段氮?dú)庋h(huán)。由于中試裝置規(guī)模受限,且丙烷預(yù)冷循環(huán)的冷劑流量小,壓縮機(jī)選型較為困難,因此考慮到設(shè)備選型的限制,確定液化中試裝置規(guī)模為2萬m3/d,并將原3級(jí)節(jié)流簡(jiǎn)化成丙烷2級(jí)節(jié)流工藝,即液化段和過冷段氮?dú)庋h(huán)采用2級(jí)壓縮加末級(jí)膨脹壓縮工藝,具體流程如圖1所示。
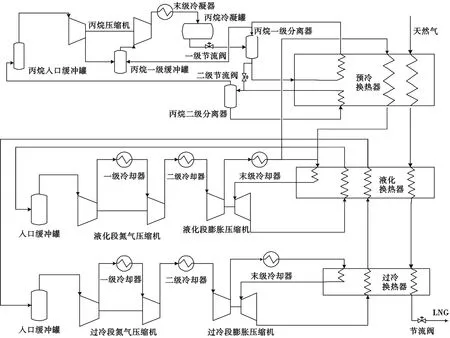
圖1 FLNG液化中試裝置流程示意圖
該中試裝置建成后經(jīng)過1個(gè)月的系統(tǒng)調(diào)試,72 h考核液化能力達(dá)2.4萬m3/d,超過了設(shè)計(jì)液化能力,裝置測(cè)試達(dá)標(biāo)后開車進(jìn)行了3個(gè)月的試驗(yàn)測(cè)試,驗(yàn)證了冷卻溫度、天然氣壓力對(duì)液化工藝的影響,并進(jìn)行了液化單元快速開車及停車方案試驗(yàn)。
2 試驗(yàn)及結(jié)果分析
2.1 快速開車試驗(yàn)
從作業(yè)安全考慮,F(xiàn)LNG液化裝置在惡劣海況條件下必須停產(chǎn),待環(huán)境條件好轉(zhuǎn)后重新開車運(yùn)行,因此,液化裝置需要具有快速開車的能力,這樣才能保證其年產(chǎn)量。一般陸上液化裝置開車順序?yàn)橄乳_啟高溫段制冷循環(huán),待降溫至設(shè)計(jì)值后再開啟低溫段循環(huán),因此該新型FLNG液化工藝中試裝置試驗(yàn)工況選取先開啟丙烷制冷系統(tǒng)(丙烷壓縮機(jī)啟動(dòng)后,預(yù)冷換熱器的溫度在30 min內(nèi)降到設(shè)計(jì)溫度-37 ℃,過冷段氮?dú)鈮嚎s機(jī)制冷循環(huán)和液化段氮?dú)鈮嚎s機(jī)制冷循環(huán)可略有間隔開啟),開車過程中嚴(yán)格控制膨脹壓縮機(jī)轉(zhuǎn)速,保證裝置開車?yán)鋮s過程滿足設(shè)備降溫速度的要求。圖2為FLNG液化工藝中試裝置快速開車過程中換熱器降溫曲線,可以看出,開車3 h內(nèi)冷箱內(nèi)溫度可降低到接近設(shè)計(jì)溫度;通入原料氣后再經(jīng)過2 h升負(fù)荷操作,裝置液化能力可以達(dá)到設(shè)計(jì)值,冷箱系統(tǒng)溫度達(dá)到穩(wěn)定,裝個(gè)裝置達(dá)到穩(wěn)定運(yùn)行狀態(tài)。
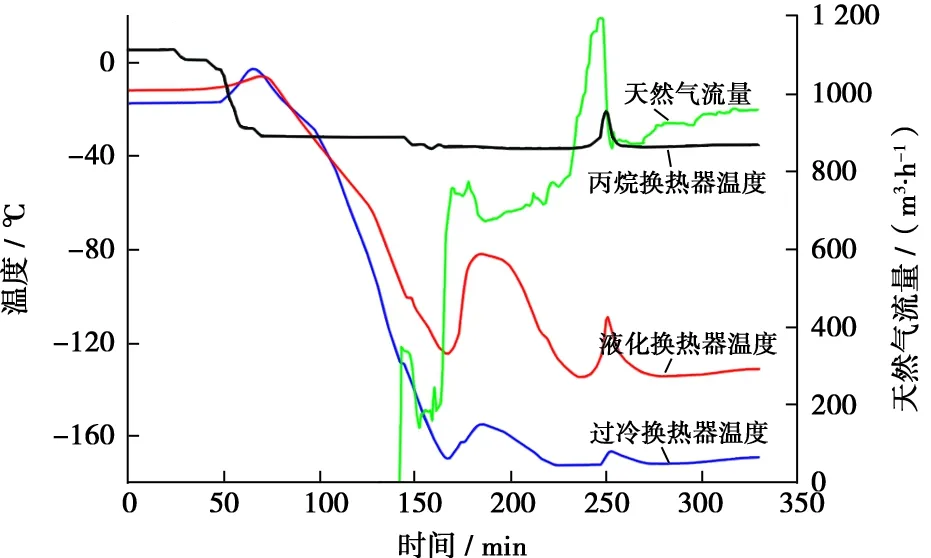
圖2 FLNG液化中試裝置快速開車的換熱器降溫曲線
由于中試裝置工藝流程設(shè)計(jì)中丙烷系統(tǒng)并不與過冷段氮?dú)鈸Q熱,所以丙烷系統(tǒng)降溫過程相對(duì)獨(dú)立,可以選擇在氮?dú)庋h(huán)降溫過程中開啟,不影響開車速度。通過對(duì)不同開車方案進(jìn)行試驗(yàn),確定液化段和過冷段的開車順序是先開過冷段膨脹制冷系統(tǒng),再開液化段氮?dú)馀蛎浿评湎到y(tǒng),主要原因如下:
1) 在未通入天然氣前,冷箱降溫過程中液化段氮?dú)馀蛎泬嚎s機(jī)和過冷段氮?dú)馀蛎泬嚎s機(jī)的制冷能力均較強(qiáng),冷箱的降溫時(shí)間主要取決于換熱器的降溫速度。
2) 過冷換熱器溫度最低,開車時(shí)首先進(jìn)行降溫,這樣能有效縮短開車時(shí)間,因此優(yōu)先啟動(dòng)過冷段氮?dú)庵评溲h(huán)。
值得注意的是,在先開啟丙烷制冷循環(huán)時(shí),預(yù)冷冷箱的降溫過快,降溫速度較難控制,分析認(rèn)為主要是由于丙烷冷劑為相變制冷,丙烷純介質(zhì)飽和溫度與壓力相對(duì)應(yīng),即控制節(jié)流壓力后冷劑進(jìn)入冷箱的溫度也已固定,所以建議丙烷預(yù)冷以低壓小流量工況開啟或利用氮?dú)庵评溲h(huán)先預(yù)冷,以防止局部驟冷造成冷箱的損壞。
另外,中試裝置在進(jìn)行快速開車時(shí),丙烷可以液態(tài)補(bǔ)充的方式添加至分離罐中,氮?dú)庀到y(tǒng)在開車過程中需要連續(xù)補(bǔ)充,且補(bǔ)充量較大(圖3),分析認(rèn)為主要是由于中試裝置內(nèi)的冷劑氮?dú)庥稍囼?yàn)現(xiàn)場(chǎng)的空壓制氮系統(tǒng)供給,系統(tǒng)操作壓力為600 kPa,故氮?dú)庀到y(tǒng)開車前充壓并維持600 kPa的壓力,但在氮?dú)庵评湎到y(tǒng)啟動(dòng)后,隨著氮?dú)庀到y(tǒng)的壓力建立和溫度降低,氮?dú)庋a(bǔ)充量逐漸增大。由于國產(chǎn)氮?dú)馀蛎泬嚎s機(jī)密封泄漏較大,對(duì)氮?dú)獾难a(bǔ)充量要求較高,中試裝置穩(wěn)定運(yùn)行時(shí)液化段氮?dú)庀到y(tǒng)的氮?dú)庋a(bǔ)充量約100 m3/h,過冷段氮?dú)庀到y(tǒng)的氮?dú)庋a(bǔ)充量約50 m3/h。快速開車初期短時(shí)間內(nèi)液化系統(tǒng)氮?dú)庋a(bǔ)充量達(dá)到200 m3/h,過冷系統(tǒng)氮?dú)庋a(bǔ)充量達(dá)到70 m3/h,因此,快速開車過程中對(duì)氮?dú)庋a(bǔ)充量需求巨大,最大需求量接近正常補(bǔ)充需求的2倍。所以,大型FLNG液化系統(tǒng)對(duì)氮?dú)庋a(bǔ)充量峰值要求將更大,要實(shí)現(xiàn)裝置的快速開車,需要在氮?dú)庀到y(tǒng)能力設(shè)計(jì)時(shí)予以充分考慮。
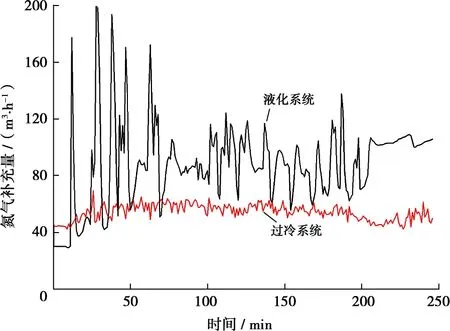
圖3 LNG液化中試裝置開車過程中氮?dú)庋a(bǔ)充量變化情況
2.2 快速停車試驗(yàn)
FLNG液化裝置在發(fā)生泄漏或其他故障時(shí)需要進(jìn)行快速停車,因此在中試裝置穩(wěn)定運(yùn)行過程中需要測(cè)試裝置快速停車性能。試驗(yàn)過程中關(guān)斷天然氣的管道閥門,在天然氣供應(yīng)中斷情況下逐漸關(guān)閉過冷段氮?dú)鈮嚎s機(jī)、液化段氮?dú)鈮嚎s機(jī)和丙烷壓縮機(jī)。其中,氮?dú)鈮嚎s機(jī)停車時(shí),先開啟壓縮機(jī)入口回流閥對(duì)出口壓力進(jìn)行泄壓,低壓壓力升高后再開啟壓力調(diào)節(jié)閥進(jìn)行氮?dú)夥趴眨趬嚎s機(jī)的高低壓壓差減小后關(guān)閉壓縮機(jī)的入口切斷閥對(duì)透平膨脹機(jī)進(jìn)行停車操作,氮?dú)鈮嚎s機(jī)的防喘振閥全開后關(guān)閉壓縮機(jī)電機(jī);天然氣系統(tǒng)停車時(shí),先關(guān)小節(jié)流閥開度,避免制冷系統(tǒng)停車后冷箱快速復(fù)溫,在節(jié)流閥小開度下對(duì)天然氣系統(tǒng)進(jìn)行泄壓,壓力達(dá)到常壓后關(guān)閉節(jié)流閥和LNG管道上的切斷閥。經(jīng)測(cè)試,停車過程中試裝置的停車時(shí)間約5 min,氮?dú)庀到y(tǒng)高低壓壓力降低到500 kPa的時(shí)間約為50 min,停車后冷箱進(jìn)入復(fù)溫階段。
另外,在海上實(shí)際工況中,停車問題解決后可能會(huì)盡快再次開車,因此對(duì)中試裝置進(jìn)行了停車后的復(fù)溫速度測(cè)試,用以制定不同停車時(shí)間后的重新開車操作程序,試驗(yàn)結(jié)果見圖4。從圖4可以看出,系統(tǒng)停車后初始時(shí)溫度升高速度較快,隨著溫度的升高,溫升速率減緩。停車時(shí),預(yù)冷換熱器溫度為-36 ℃,液化換熱器溫度-120 ℃,過冷換熱器溫度-160 ℃;停車1 d后,預(yù)冷換熱器溫度升高到1 ℃,液化換熱器溫度升高到-44 ℃,過冷換熱器溫度升高到-82 ℃,冷箱液化段和過冷段仍處于相對(duì)溫度較低的狀態(tài),裝置可以采用冷啟動(dòng)程序,停車5 d后,冷箱溫度基本復(fù)溫到常溫。
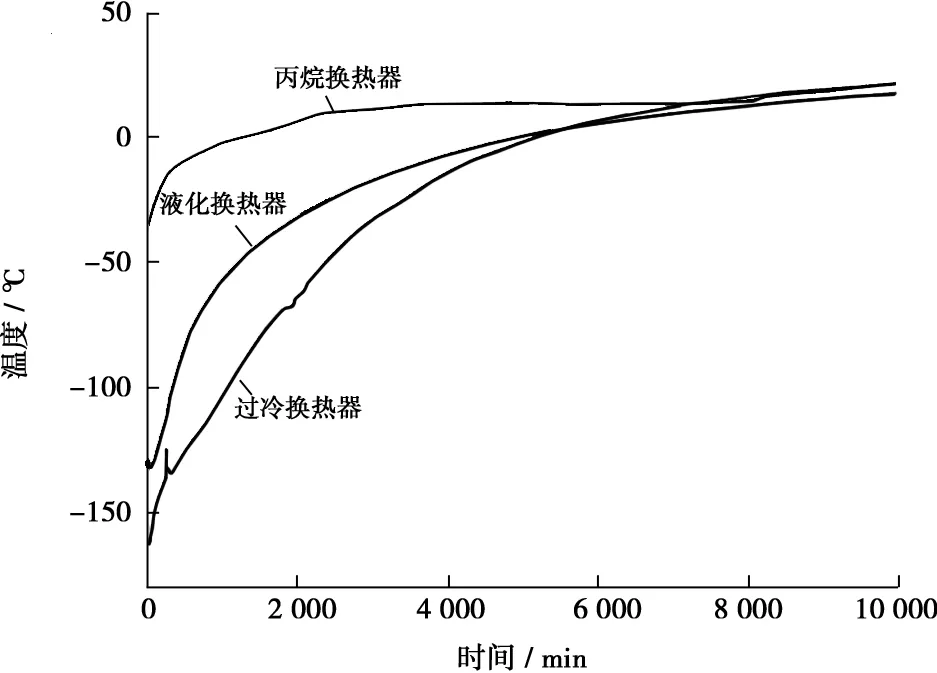
圖4 FLNG液化中試裝置停車后冷箱復(fù)溫曲線
2.3 冷卻溫度影響試驗(yàn)
對(duì)于FLNG液化裝置,外界溫度直接影響冷卻介質(zhì)的溫度,進(jìn)而影響系統(tǒng)的冷卻溫度和裝置的運(yùn)行參數(shù)。大型FLNG液化裝置通常采用海水作為冷卻介質(zhì),若取水深度足夠大,環(huán)境溫度對(duì)海水溫度影響很小。本FLNG中試裝置采用空氣冷卻,全天最高冷卻溫度約30 ℃,最低冷卻溫度約18 ℃,氣溫變化12 ℃左右,試驗(yàn)期間利用冷卻空氣溫度的變化模擬海水溫度季節(jié)變化產(chǎn)生的影響。
圖5為FLNG液化中試裝置丙烷冷卻溫度與壓縮機(jī)出口壓力關(guān)系圖,可以看出,丙烷壓縮機(jī)出口壓力受冷卻溫度影響明顯,冷卻溫度越高,丙烷冷凝的壓力越高。隨著丙烷壓縮機(jī)的出口壓力提高,丙烷壓縮機(jī)的功率也會(huì)相應(yīng)增加。經(jīng)試驗(yàn)測(cè)試,在保證LNG出冷箱溫度不變的情況下,隨著冷卻介質(zhì)溫度的降低,丙烷壓縮機(jī)的功耗減少,天然氣液化所需要的冷量減少,天然氣處理能力增加。圖6為FLNG液化中試裝置液化能力及單位能耗隨冷卻溫度變化曲線,冷卻溫度降低12 ℃條件下,天然氣處理能力增加4.26%,裝置的單位能耗減少約5%。
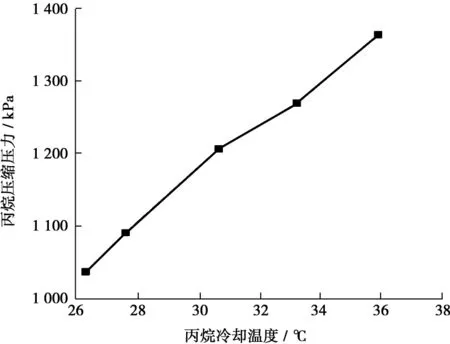
圖5 FLNG液化中試裝置丙烷冷卻溫度與壓縮機(jī)出口壓力的關(guān)系
另外,根據(jù)理論模擬優(yōu)化計(jì)算,液化段氮?dú)獠糠至鹘?jīng)丙烷預(yù)冷換熱器進(jìn)行預(yù)冷后會(huì)降低天然氣單位液化能耗,增加天然氣處理量。為進(jìn)行此項(xiàng)驗(yàn)證,在FLNG液化中試裝置的預(yù)冷系統(tǒng)預(yù)留了一段液化段氮?dú)饨涌冢囼?yàn)過程中通過調(diào)節(jié)預(yù)冷氮?dú)獾牧髁浚治鰧?duì)裝置運(yùn)行的影響。FLNG液化中試裝置天然氣處理量與氮?dú)忸A(yù)冷流量關(guān)系的試驗(yàn)結(jié)果以及與理論模擬計(jì)算結(jié)果對(duì)比如圖7所示,可以看出,隨著預(yù)冷氮?dú)饬康脑黾樱烊粴馓幚砹坑兴黾樱陬A(yù)冷氮?dú)饬吭黾拥侥骋恢岛螅烊粴馓幚砹块_始下降(試驗(yàn)中由于氮?dú)忸A(yù)冷管路的調(diào)節(jié)閥最大流量只能達(dá)到743 m3/h)。試驗(yàn)測(cè)得的天然氣處理量比理論計(jì)算值高,這主要是受設(shè)備選型較大以及壓縮機(jī)能力比設(shè)計(jì)值高的影響,但二者的變化趨勢(shì)一致,驗(yàn)證了理論模擬優(yōu)化的準(zhǔn)確性。
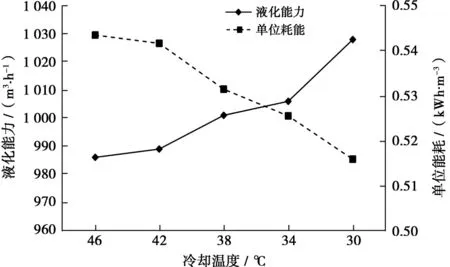
圖6 FLNG液化中試裝置液化能力及比功耗隨冷卻溫度變化曲線
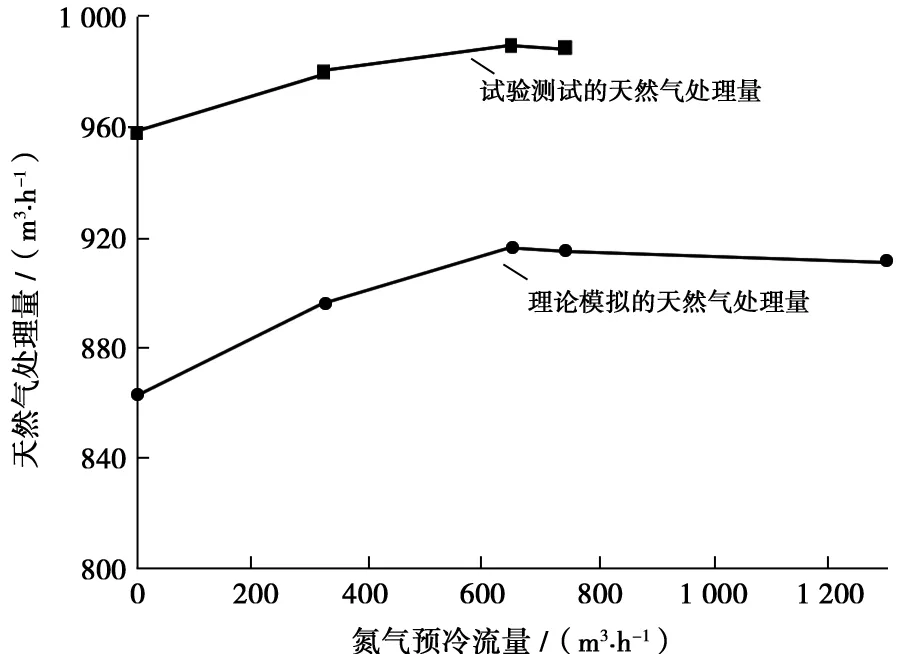
圖7 FLNG液化中試裝置天然氣處理量與氮?dú)忸A(yù)冷流量的關(guān)系
2.4 天然氣壓力適應(yīng)性試驗(yàn)
天然氣壓力決定了其液化溫度和液化所需要的冷量,壓力越高,氣體液化溫度越高,且液化所需要的冷量越低。FLNG液化中試裝置在生產(chǎn)初期可充分利用原料氣的壓力,隨著氣田的開采,天然氣壓力逐漸降低,在生產(chǎn)后期需要評(píng)估是進(jìn)行低壓液化還是增加原料氣壓縮機(jī)。試驗(yàn)中通過調(diào)節(jié)進(jìn)入液化裝置的天然氣壓力,檢驗(yàn)裝置在不同壓力下的運(yùn)行情況。不同天然氣壓力FLNG液化中試裝置的運(yùn)行參數(shù)如表1所示,降低天然氣壓力時(shí),維持制冷系統(tǒng)參數(shù)基本不變,通過調(diào)節(jié)天然氣的流量保證天然氣液化裝置的LNG出口溫度基本不變。
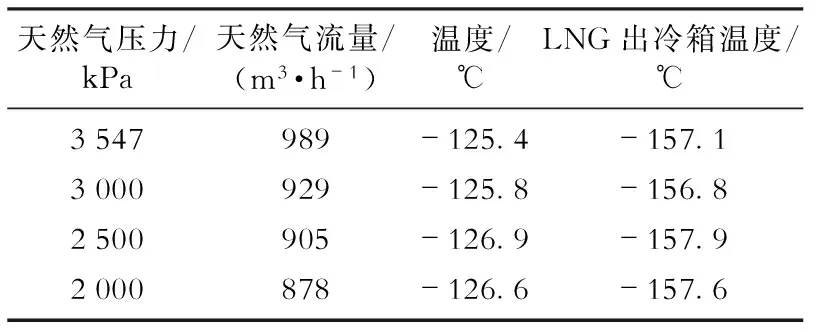
表1 不同天然氣壓力下FLNG液化中試裝置的運(yùn)行參數(shù)
圖8為壓縮機(jī)功率和天然氣處理量與天然氣壓力的關(guān)系,可以看出,在保證制冷系統(tǒng)參數(shù)基本不變的情況下,天然氣處理量隨著天然氣壓力的降低而降低,天然氣壓力由3 547 kPa降低到2 000 kPa時(shí),天然氣處理能力降低11.2%。
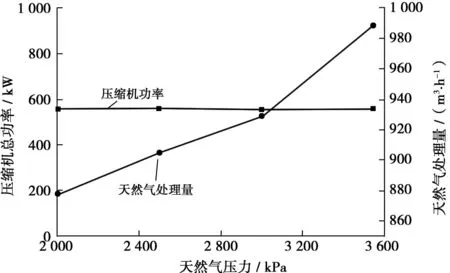
圖8 FLNG液化中試裝置壓縮機(jī)功率和天然氣處理量與天然氣壓力的關(guān)系
另外,根據(jù)理論模擬和試驗(yàn)測(cè)得的壓縮機(jī)功率及天然氣處理量分別計(jì)算出不同天然氣壓力下的單位液化能耗(圖9),對(duì)比可以看出,單位液化能耗隨著天然氣壓力下降而升高,而且理論模擬和試驗(yàn)結(jié)果一致,變化幅度也一致。
3 結(jié)論
1) FLNG液化中試裝置快速開車時(shí)間受板翅式換熱器的降溫速度要求限制,先開啟過冷氮?dú)庋h(huán)、再開啟液化段氮?dú)庋h(huán)是達(dá)產(chǎn)最快的開車程序,開車5 h可以達(dá)到設(shè)計(jì)生產(chǎn)負(fù)荷,開車過程中對(duì)氮?dú)庋a(bǔ)充量需求較大,峰值可達(dá)正常補(bǔ)充量的2倍。
2) FLNG液化中試裝置具有快速停車性能,可以在5 min內(nèi)關(guān)停,冷箱恢復(fù)常溫需要5 d時(shí)間。
3) 隨著混合冷劑級(jí)間冷卻溫度降低,F(xiàn)LNG液化中試裝置液化能耗降低,試驗(yàn)過程中冷卻溫度降低12 ℃條件下天然氣處理能力增加4.26%,液化單位能耗減少約5%。
4) 隨著天然氣壓力降低,F(xiàn)LNG液化中試裝置液化能力下降,試驗(yàn)過程中天然氣壓力從3 547 kPa降低到2 000 kPa時(shí)天然氣的處理能力降低11.2%。
[1] 薄玉寶.浮式液化天然氣(FLNG)技術(shù)在中國海上開發(fā)應(yīng)用探討[J].中國海洋平臺(tái),2013,28(3):1-5,9.
Bo Yubao.Floating liquefied natural gas (FLNG) technology in China offshore development application to discussion[J].China Offshore Platform,2013,28(3):1-5,9.
[2] GIMOUR N,DEVENREY D.Floating LNG shell’s recent history and current approach[C].Algeria:The LNG 16 Conference,2010.
[3] 浦暉,陳杰.LNG-FPSO液化工藝方案比選研究[J].制冷技術(shù),2011,21(4):31-34.
Pu Hui,Chen Jie.Study on comparative selection of LNG-FPSO liquefaction process schemes[J].Refrigeration Technology,2011,21(4):31-34.
[4] 顧妍,巨永林.浮式天然氣液化工藝與設(shè)備的適用性分析[C].上海:上海市制冷學(xué)會(huì)二〇〇七年學(xué)術(shù)年會(huì)論文集,2007.
[5] 朱建魯,李玉星,王武昌,等.海上天然氣液化工藝流程優(yōu)選[J].天然氣工業(yè),2012,32(3):98-104.
Zhu Jianlu,Li Yuxing,Wang Wuchang,et al.Optimization selection of natural gas liquefaction process for FLNG[J].Natural Gas Industry,2012,32(3):98-104.
[6] 朱建魯,李玉星,王武昌,等.CO2預(yù)冷雙氮膨脹天然氣液化工藝的海上適應(yīng)性分析[J].天然氣工業(yè),2012,32(4):89-95.Zhu Jianlu,Li Yuxing,Wang Wuchang,et al.Analysis on the adaptability of CO2pre-cooling dual nitrogen expanded liquefaction process for FLNG[J].Natural Gas Industry,2012,32(4):89-95.
(編輯:葉秋敏)
Experimental analysis of propane pre-cooling dual nitrogen expansion liquefaction process on pilot FLNG plant
Li Endao Yin Quansen Liu Miaoer Chen Jie Zhang Shuxun
(CNOOCGas&PowerGroup,Beijing100028,China)
A 20,000 m3/d pilot plant was built to verify the feasibility of the new propane pre-cooling liquefaction process for FLNG by dual nitrogen expansion which had been proposed by CNOOC. The influences of cooling temperature and natural gas pressure on the liquefaction process were verified by experiments. And the quick start-up and shut-down scheme for the liquefaction unit were also tested in the experiments. The experimental results show that the power consumption will decrease with temperature dropping. Natural gas processing capacity was increased by 4.26%, and the power consumption of the unit was reduced by 5% upon decreasing the cooling temperature of refrigerant by 12 ℃. The minimum quick start-up time for FLNG is mainly limited by the requirements on the cooling speed of the plate-fin heat exchanger. So the quickest procedure is to start the deep cooling nitrogen refrigeration cycle to let the low temperature parts to cool down first, and then start the liquefaction nitrogen circle to increase the liquefaction capacity. The full capacity of the pilot FLNG plant can be realized within 5 hours from initial start. The whole pilot plant can be stopped safely in 5 minutes, and the warm up for the cold box of the plant will last for 5 days. The liquefaction capacity will decrease with the natural gas pressure dropping. Liquefaction capacity decreased by 11.2% in the experiment when the gas pressure was reduced from 3 547 kPa to 2 000 kPa. The analysis results of this paper provide effective technical support for the engineering of large-scale FLNG liquefaction plants.
FLNG; propane pre-cooling dual nitrogen expansion; liquefaction process;pilot plant; experiment analysis
*“十二五”國家科技重大專項(xiàng)課題“大型FLNG/FLPG、FDPSO關(guān)鍵技術(shù)(編號(hào):2015ZX05026-006)”下屬子課題“FLNG液化中試裝置研制和現(xiàn)場(chǎng)試驗(yàn)研究(編號(hào):2011ZX05026-006-01)”部分研究成果。
李恩道,男,工程師,現(xiàn)主要從事天然氣液化設(shè)備及浮式天然氣液化技術(shù)研發(fā)設(shè)計(jì)工作。地址:北京市朝陽區(qū)太陽宮南街6號(hào)院海油大廈(郵編:100028)。電話:010-84526514。E-mail:lied@cnooc.com.cn。
1673-1506(2016)04-0149-06
10.11935/j.issn.1673-1506.2016.04.024
TE646
A
2015-10-29 改回日期:2015-12-26
李恩道,尹全森,劉淼兒,等.FLNG丙烷預(yù)冷雙氮膨脹液化工藝中試裝置試驗(yàn)分析[J].中國海上油氣,2016,28(4):149-154.
Li Endao,Yin Quansen,Liu Miaoer,et al.Experimental analysis of propane pre-cooling dual nitrogen expansion liquefaction process on pilot FLNG plant[J].China Offshore Oil and Gas,2016,28(4):149-154.

