分辨矩陣在邏輯優化中的應用

閆心怡，溫 馨，陳澤華+

1.太原理工大學 電氣與動力工程學院，太原 030024

2.太原理工大學 大數據學院，太原 030024

組合邏輯電路[1]由門電路組成，門之間的相互連接形成了邏輯網絡。邏輯網絡可由布爾函數或真值表來描述。通過化簡布爾函數或真值表，可以減少邏輯網絡的復雜性，從而提高電路的可靠性并降低系統功耗。K-map（Karnaugh map）[1]是典型的圖形表示的布爾函數化簡方法，當輸入變量超過5 時其圖形難以理解。Q-M（Quine-McCluskey algorithms）[1]方法更便于計算機計算，但是Q-M 算法的運行時間隨變量數量呈指數增長。隨著電路規模不斷擴大，數據挖掘理論的迅速發展，從知識工程角度重新考慮邏輯電路優化，是一種新的思路。

經典粗糙集理論由Pawlak 提出，除了通過定義上、下近似完成知識的近似表達，還可以基于等價關系處理信息系統，在保證信息不減的前提下實現知識約簡或規則提取。

Skowron 教授提出的不可分辨矩陣[2-3]是信息系統屬性約簡和規則提取的經典方法，在此基礎上衍生出很多相關改進算法[4-11]，有學者將其與覆蓋[6]、模糊粗糙集[7]啟發式算子聯系起來構建新的辨識矩陣，使之能夠對一致、不一致系統進行更為有效的屬性約簡和規則提取。近年來，學者將分辨矩陣和形式概念分析[12-14]結合起來，基于分辨矩陣的方法也在形式概念分析中發展起來。

在邏輯電路的分析與設計中，真值表用來表征數字邏輯電路輸入與輸出之間的邏輯關系，真值表約簡是邏輯優化的理論基礎。本文將真值表看作邏輯信息系統（logic information system，LIS）[15]，在傳統分辨矩陣基礎上構造了粒分辨矩陣，與多粒度形式概念分析的類屬性塊方法[16]中一樣，試圖尋找決策蘊含與不同屬性組合之間的關系，但是不同的是本文通過定義信息粒來分析屬性與決策間的關系，將邏輯電路化簡轉化為基于粒分辨矩陣的LIS 最簡規則發現問題。該方法避免了傳統分辨矩陣中大量的矩陣元素計算問題，同時證明了該方法與傳統卡諾圖約簡的等價性。

1 預備知識

數字電路可以用布爾函數以及真值表進行表示。它們處理的是“0”“1”信號。

定義1（真值表）真值表是表征邏輯事件輸入和輸出之間全部可能狀態的表格，它對所有可能的邏輯輸入定義了對應的邏輯輸出，用邏輯關系的表格形式表示。真值表的輸入包括了全部n個變量的乘積項（每個變量只以原變量或反變量的形式出現一次），稱為最小項。n個輸入變量的真值表包含2n個最小項，用表示。

定義2（最小項表達式）真值表中對應所有邏輯函數值為1 的最小項之和，稱為最小項表達式。

定義3（最簡邏輯函數表達）化簡后的真值表中所有邏輯函數值為1 的條件屬性乘積項的組合稱為最簡邏輯函數表達式。

定義4[15]（邏輯信息系統）定義LIS=(U,R,V,f)為一個邏輯信息系統，其中U為論域，|U|表示論域元素個數，R=A?Y為屬性集，A={A1,A2,…,Am}表示邏輯信息系統的輸入變量（條件屬性），|A|表示條件屬性的個數，Y={Y1,Y2,…,Yn}表示邏輯信息系統的輸出變量（決策屬性），|Y|表示決策屬性的個數。V={0,1} 是屬性值的值域，f:U×R→V是一個信息函數，它指定U中每一個對象的屬性值。

真值表是一個邏輯信息系統，它的每一行代表一條邏輯規則。

特殊地，當n=1 時，這是一個多輸入單輸出邏輯信息系統。

從邏輯信息系統的角度研究真值表，可以將數字邏輯電路中的邏輯優化問題轉化為信息系統最簡單規則發現問題。

定義5（信息粒）邏輯信息系統中的任意邏輯輸入變量Ai∈A可以導出論域U的一個劃分：

式中，fAi(u)=0 表示在屬性Ai論域下具有屬性值0 的論域元素u。同樣的表示在屬性Ai下論域中具有屬性值1 的論域元素u。可以得到由輸入變量Ai推導出的等價類劃分，本文將該等價類劃分定義為信息粒。由邏輯輸入屬性Ai∈A推導出的所有信息粒構成了一個信息粒集（information granular set，IGS）。

定義6（決策類劃分）對于任何邏輯輸出屬性Yi，其屬性值也將在整個論域中劃分。定義U0=，表示輸出屬性Yi中所有屬性值為“0”的論域元素。相應地，，表示輸出屬性Yi中所有屬性值為“1”的論域元素。

顯然地，U0?U1=U，U0?U1=?。

定義7（粒分辨矩陣）本文利用等價類定義信息粒，進而構成粒分辨矩陣。對于多輸入單輸出信息系統，定義粒分辨矩陣：

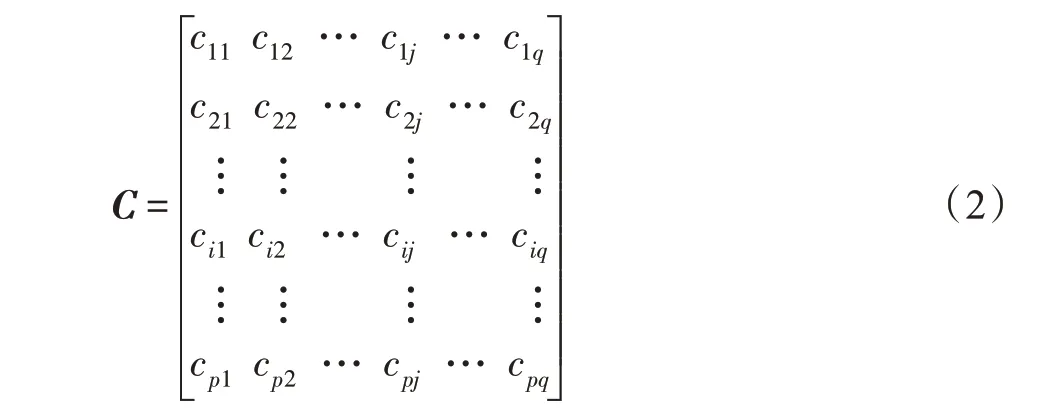
式中元素：

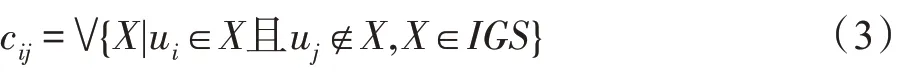
式中，cij表示信息粒集合中能夠區分元素ui∈U1與元素uj∈U0的信息粒，X表示信息粒集合中的任一元素。同時p=|U1|表示輸出屬性Yi中所有屬性值為“1”的論域元素個數。q=|U0|表示輸出屬性Yi中所有屬性值為“0”的論域元素個數。

定義8（決策規則）組織粒分辨矩陣中的元素cij，定義決策規則：

式中，ri包含所有能區分ui∈U1與uj∈U0中的所有元素，DR即為能區分等價類U0和U1的最簡規則集，dr作為其中的一條規則。

定義9（啟發式信息）在最簡規則基礎上提出啟發式信息：

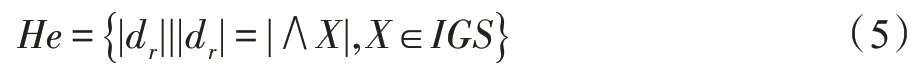
式中，|dr|表示規則的信息粒組合的個數。

2 粒分辨矩陣的邏輯表達式優化算法

根據第1 章的相關內容，本文針對真值表提出了一種基于粒分辨矩陣的約簡算法。

2.1 算法描述

算法1基于粒分辨矩陣的真值表約簡算法

輸入：真值表。

輸出：最小布爾邏輯表達式。

步驟1計算U0和U1，初始化MBE=?，計算信息粒。

步驟2計算邏輯輸出的粒分辨矩陣C。

步驟3根據粒分辨矩陣元素cij組織決策規則，計算每條規則的啟發式信息He。

步驟4對He由大到小排序，判斷每條規則是否存在新識別的論域元素。

步驟5若存在，將該條規則記錄到MBE中；同時判斷是否覆蓋U1集合中的所有元素，若覆蓋跳到步驟7，否則返回步驟4，繼續計算下一條規則。

步驟6否則，不記錄。

步驟7輸出最小布爾邏輯表達式MBE，結束。

可以證明本文所提算法與K-map方法的等價性：

對一個n行真值表，設有r個最小項F輸出變量值1 且Fi為其中一個最小項（0 ≤i≤r），則有n-r個最小項G輸出變量值0 且Gj為其中一個最小項（0 ≤j≤n-r）。

設Fi與Gj不同的輸入變量為X1,X2,…,Xs，則在卡諾圖中可以形成s組互補的包圍圈，其中任一組包圍圈中的均包含最小項Fi在卡諾圖中的“1”，而不包含Gj，因此這s組包圍圈互相為“或”關系。同理，若使得Fi與n-r個輸出變量值為0 的最小項G都區分出來，則需Fi與n-r個最小項形成的包圍圈互相為“與”關系。

粒分辨矩陣中，行為真值表中輸出為1 的最小項Fi，列為輸出為0的最小項Gj。矩陣元素cij為Fi與Gj不同的邏輯輸入變量，cij中任一變量均可區分Fi與Gj，故cij中，各變量為“或”關系，cij=X1∨X2∨…∨Xs，cij和Fi所在s組包圍圈對應。同理，若欲得到Fi與所有輸出變量值為0 的最小項G都不同的邏輯輸入變量，需n-r個cij為相“與”關系，即ci1∧ci2∧…∧cir。由上述分析可知，粒分辨矩陣方法與卡諾圖方法原理相同，故粒分辨矩陣方法等價于卡諾圖方法。

2.2 實例說明

邏輯電路與邏輯表達式是可以轉化為真值表來表示的，本文將通過例2 來說明算法1 的實施過程。

例2對于圖2 邏輯電路圖，其函數式為Y=。可以將圖1 轉化為如表1 所示真值表，對于有3 個邏輯輸入的邏輯電路，其對應的真值表有8 行數據。

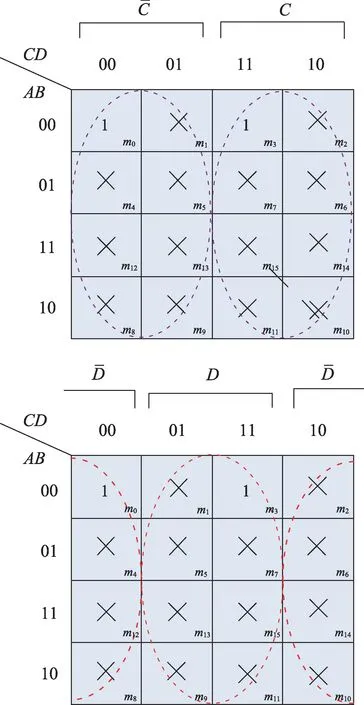
Fig.1 Complementary encirclement diagram圖1 包圍圈示意圖

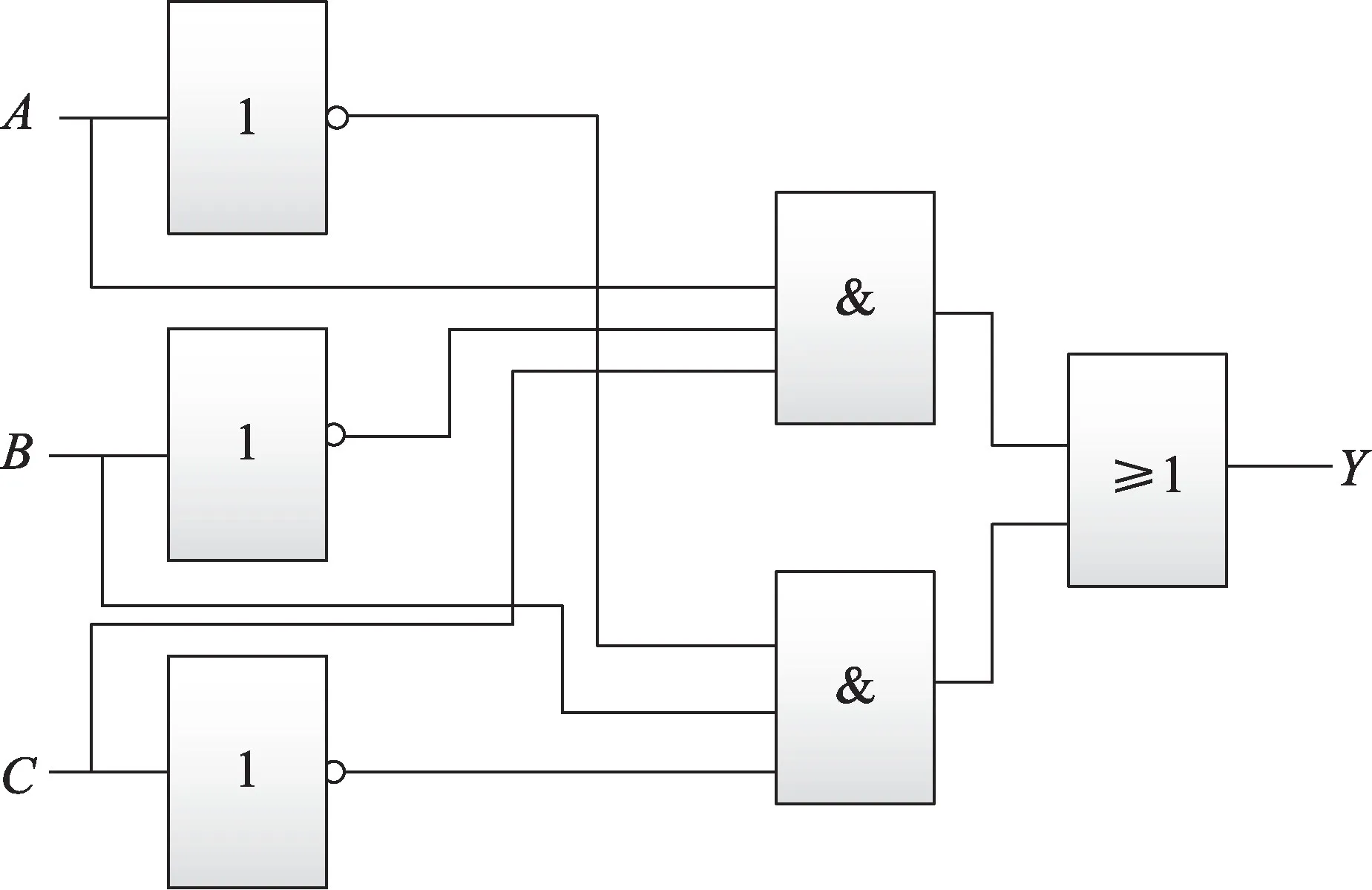
Fig.2 Logic circuit diagram圖2 邏輯電路圖

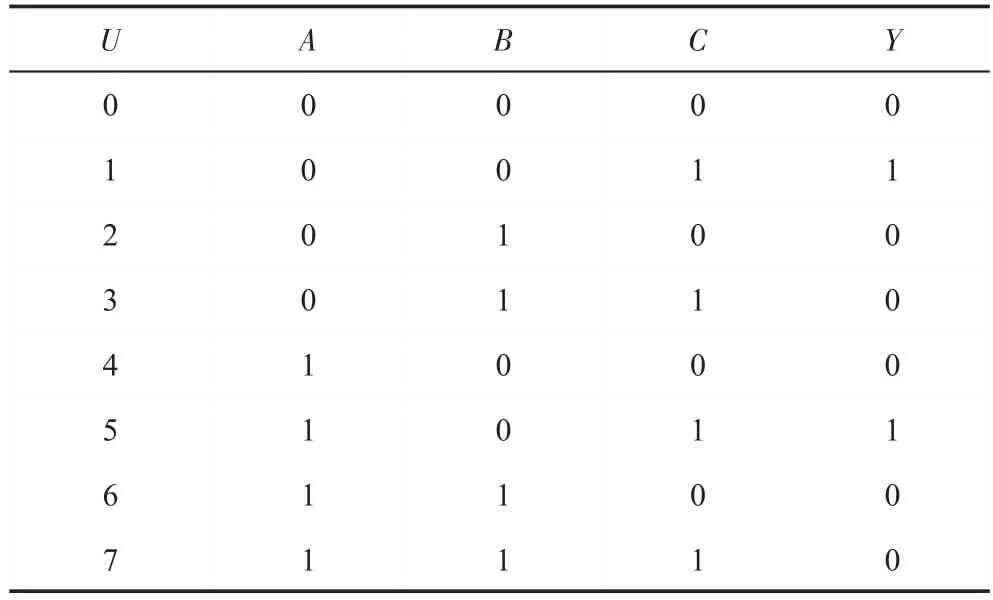
Table 1 Truth table表1 真值表

本例以邏輯輸出Y為例說明本文算法的運算過程，如表1 所示，可知：

論域U={0,1,2,3,4,5,6,7}，邏輯輸入屬性為A={A,B,C}，邏輯輸出屬性為Y，根據定義4 可以得到：

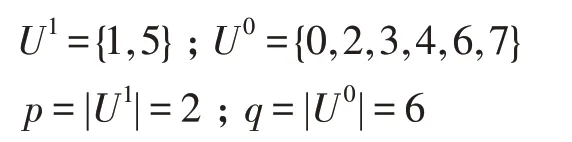
同理可得：

構造粒分辨矩陣：

同理可得矩陣中的其他元素，得到如上矩陣計算結果。

根據定義8 計算決策規則可得：

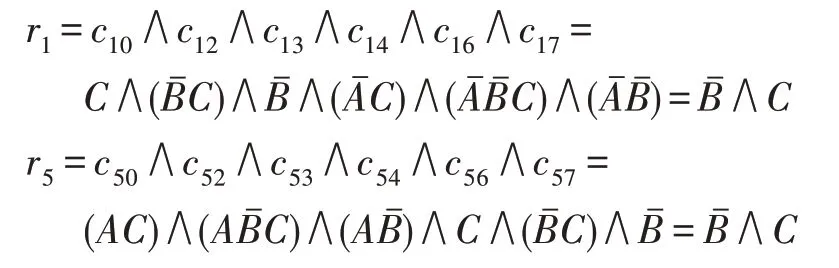
最后根據式（4）可以得到：

Table 2 Heuristic information表2 啟發式信息

根據文獻[1]中的卡諾圖化簡方法首先得到圖3，由圖可知卡諾圖化簡結果為。對比兩種方法的結果可知，本文算法所得結果與卡諾圖化簡結果一致。

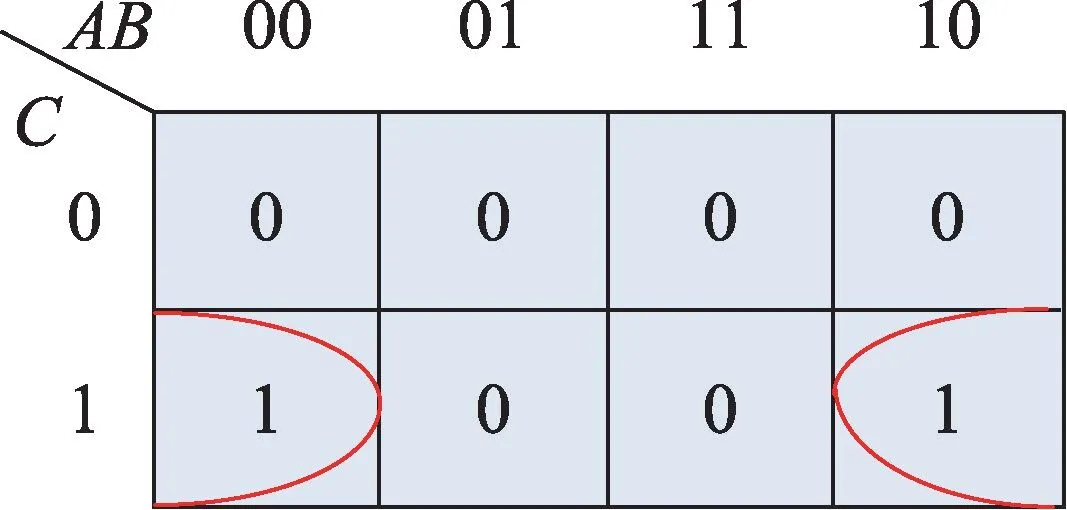
Fig.3 Karnaugh map reduction diagram圖3 卡諾圖化簡示意圖

3 算法分析

K-map 方法使用簡單直觀，但是圖形表示難以描述5 個以上的輸入變量；Q-M 算法使得K-map 方法易于在計算機上實現。對于含有m個輸入的真值表，|A|=m,|U|=2m，Q-M 算法的時間復雜度為O(|U|×3|A|)，即O(2m×3m)。在粒矩陣法（granular matrix reduction algorithm，GMRA）[15]中，用粒度計算和矩陣來區分真值表中的所有“1”，將邏輯化簡問題轉化為布爾矩陣運算的問題，算法的時間復雜度為O(|U|2×|A|×2|A|)，即O(m×23m)。文獻[17]提出的變粒度真值表約簡算法（variable granularity reduction algorithm，VGRA），隨著真值表的輸入邏輯變量的粒度變化，通過引入標記矩陣和啟發式算子，對大規模真值表進行知識約簡，其算法復雜度為O(|U|×|A|×2|A|)，即O(m×22m)。文獻[18]將MIMO（multiple input multiple output）真值表轉化為決策形式背景，將真值表的約簡問題轉化為決策形式背景的最簡規則提取過程，提出一種基于FCA（formal concept analysis）的MIMO 真值表并行約簡算法，其算法的復雜度為O(|U|×|A|)+O(|U|2×|A|2lb(|U|×|A|))，即O(m×2m)+O(22m×m3×lbm)。

本文算法中，粒分辨矩陣C=[cij]的規模為p×q，其中p+q=2m，而經典分辨矩陣的規模為2m×2m。從矩陣的規模可以看到，矩陣復雜度大大下降。生成本文提出的粒分辨矩陣C的計算復雜度O(p×q)，決策規則的計算復雜度為O(q)，規則提取過程的計算復雜度為O(p)，故整個算法復雜度為O(p2×q2)，在最壞情況下也遠小于O(22m-1)。各算法復雜度對比如表3 所示。

GMRA 算法復雜度以指數8 為底，Q-M 算法復雜度則以指數6 為底，VGRA 算法復雜度以指數4 為底。本文提出的GMD 算法，在傳統分辨矩陣的基礎上，簡化了矩陣的規模，避免了大量矩陣元素的計算，同時利用啟發因子的優勢，加快算法收斂速度。較Q-M 算法以及其他算法在計算復雜度上具有明顯的優勢。

Table 3 Complexity comparison表3 復雜度對比

4 結束語

本文將分辨矩陣應用到邏輯優化中，提出了一種獲取最小布爾表達式的方法。構造粒分辨矩陣區分真值表中的所有“1”，本文從理論證明和實例分析的角度，說明了算法的正確性和有效性。

本文的創新之處在于：（1）粒分辨矩陣與傳統的分辨矩陣不同，它既不是方陣也不對稱，大大減少了矩陣規模。（2）矩陣的元素由信息粒度（等價類代替屬性）表示，而非將屬性作為基本元素。（3）證明了本文算法與卡諾圖法的等價性。（4）以覆蓋真值表中所有的輸出“1”為終止條件，簡便運算同時避免了規則的冗余。

在下一步的研究工作中，可以繼續將該方法擴展到多輸出邏輯信息系統中。雖然從算法復雜度的角度來看，本文算法比以往算法的復雜度有所下降，但是依舊以指數形式增長。在以后的工作中可以探索并行計算方式，并能夠將相關成果和概念研究融合起來。另外本文方法還暫未推廣至普通的信息系統中，方法仍需要繼續改進擴展，這也是未來努力需要解決的問題。