標注Petri網的最小代價計劃序列估計
周廣瑞,徐淑琳,郭乙運,魯法明,岳 昊+
1.青島大學 復雜性科學研究所,山東 青島 266071
2.山東省工業控制技術重點實驗室,山東 青島 266071
3.青島港國際股份有限公司,山東 青島 266011
4.山東科技大學 計算機科學與工程學院,山東 青島 266590
離散事件系統是由事件序列驅動的一種動態系統,可以通過一組狀態和一些驅動狀態改變的事件來描述[1]。典型的離散事件系統有柔性制造系統、交通系統以及通信網絡系統等。Petri 網[2-3]是系統建模和分析的工具,能夠簡便地描述系統的演化過程。Petri 網作為一種形式化工具被用于解決許多有價值的問題,例如,柔性裝配系統的監督控制[4-5]、死鎖控制[6-9]、業務流程管理[10-11]等。
文獻[12-13]研究了基于變遷觀測的Petri 網的標識估計問題,將觀測信息來源于變遷發生的Petri 網稱為標注Petri 網。在標注Petri 網中估計最小初始標識,可用于解決制造系統中已知制造流程求解最小資源消耗的最優化問題。在制造系統中,規劃出以最小成本完成任務的制造流程,轉化為標注Petri 網中的最小代價計劃序列的估計問題[14-16]。文獻[14]提出了一種用于計算最小代價變遷序列的動態規劃算法,并證明了標識數目是關于標注序列長度k的多項式函數,最小代價變遷序列即為所求的最小代價計劃序列。文獻[16]提出在標注Petri 網中可通過構建一種特殊可達圖的方法來尋找最小代價變遷發生序列。
在現有的文獻中,回溯法作為一種系統化的搜索方法常用于最優解的求取問題,通過目標函數和約束條件來避免無效搜索,剔除冗余節點,減少搜索的節點數目[17]。文獻[18]應用回溯法求解帶時間窗和同時送取貨的車輛最優路徑問題。文獻[19]解決無線傳感器網絡的確定性調度問題,基于回溯法能夠獲得近似最優調度解,有效降低計算復雜度。文獻[20]應用回溯法解決云計算中多任務執行不協調的問題,節約了計算時間。文獻[21]應用回溯法解決安全業務可行性的時間和空間失衡問題,付出的空間代價較小,且具有良好的時間性能。
在制造系統標注Petri 網模型中估計最小代價計劃序列,有助于達到以最小成本完成生產任務的目的。本文應用回溯法對標注Petri 網的最小代價計劃序列進行估計,達到減少計算量、提高工作效率的目標。應用本文方法,當觀測到一個標注時,優先發生代價小的變遷,根據深度優先搜索的策略能夠獲得一個當前最小代價變遷序列。以其作為約束條件,在搜索其他路徑時,能夠避免一些不滿足約束條件的變遷發生,并剔除搜索路徑中的剩余標識,最終通過遍歷解空間樹獲得系統的最小代價變遷序列。基于回溯法求解標注Petri 網的最小代價計劃序列估計問題,能夠剔除冗余標識,進而刪除多余搜索標識路徑。現有文獻中的動態規劃法僅能夠合并相同標識,不能剔除標識,因此回溯法的計算量更小。針對同一實例分別采用回溯法與動態規劃法進行運算,由實驗運行結果可知,本文方法具有更高的工作效率。
1 基本概念
N=(P,T;A,W) 為一個Petri 網,其中P={p1,p2,…,pn} 是有限庫所集,T={t1,t2,…,tm} 是有限變遷集,A?(P×T)?(T×P)是流關系集合,W:A→{1,2,…}是弧上的權重函數。在Petri 網模型示意圖中,空心圓圈代表庫所,庫所中的托肯用實心圓點表示,黑色實線代表變遷,有向箭頭代表流關系。


以圖1 所示的標注Petri 網模型為例,庫所集P={p1,p2,…,p9};變遷集T={t1,t2,…,t7};標注集Σ={a,b,c,d,e};標注函數為L(t1)=a,L(t2)=L(t3)=b,L(t4)=L(t5)=c,L(t6)=d,L(t7)=e;變遷代價為C(t1)=C(t2)=C(t5)=C(t6)=C(t7)=1,C(t3)=2,C(t4)=3。p1與p9中的托肯分別表示待加工原材料和成品,p2~p8中的托肯表示半成品,變遷t1與t7分別表示拆卸和組裝。變遷t2~t8表示半成品的加工,其中一個加工過程表示為p2t2p4t4p6t6p8。
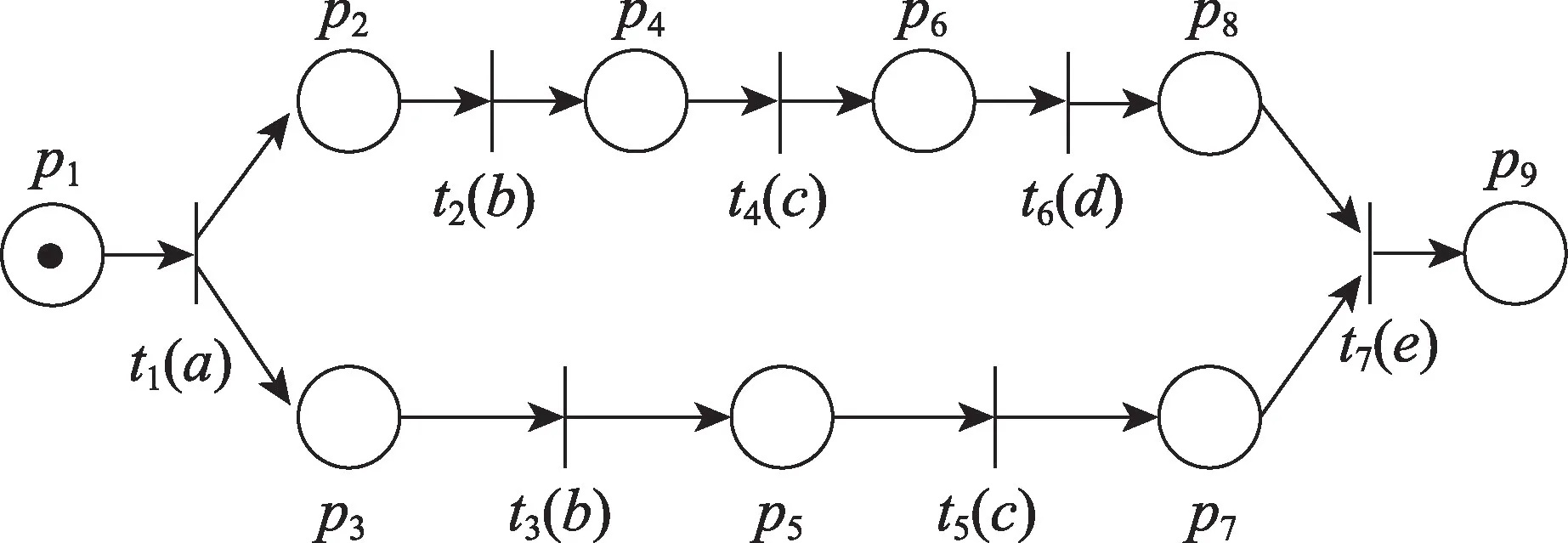
Fig.1 A labeled Petri net model圖1 一個標注Petri網模型
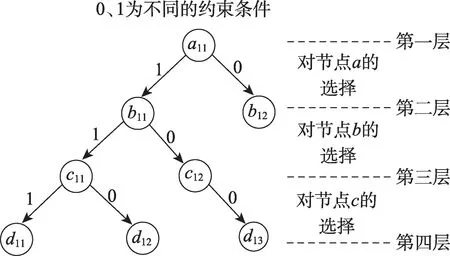
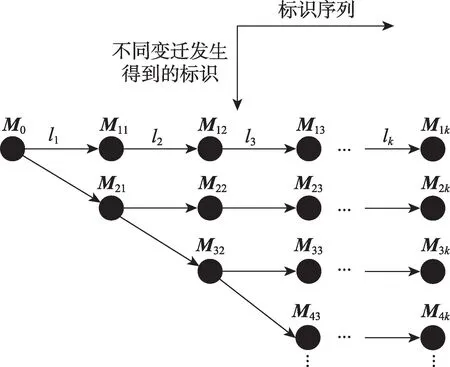
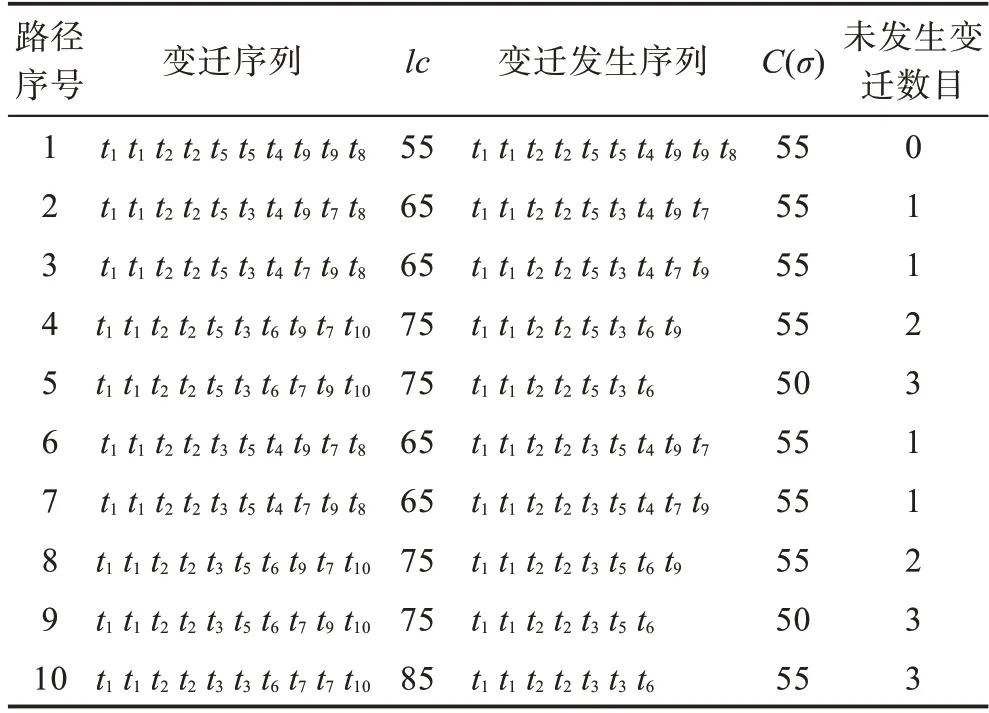
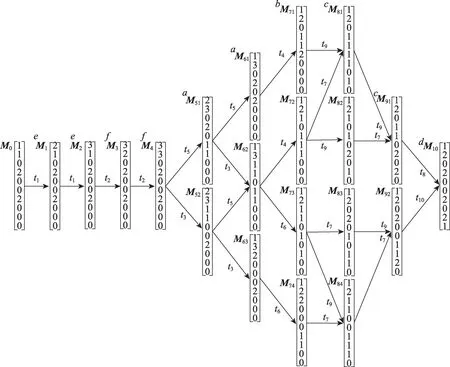
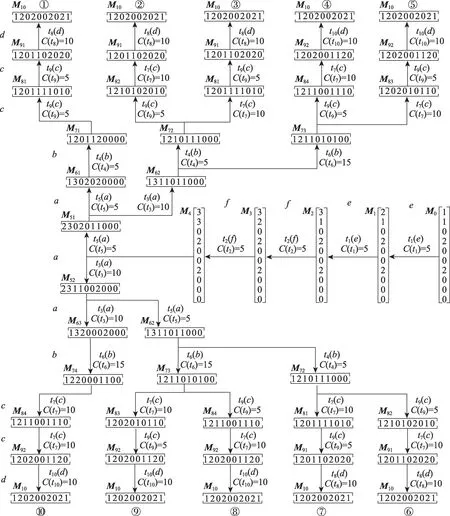
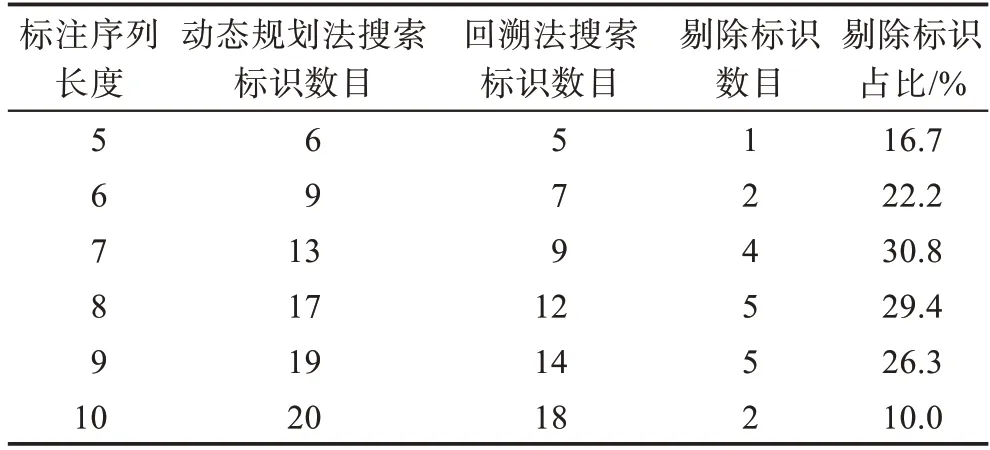
給定一個長度為2 的標注序列ω=a b,根據ω可獲得變遷發生序列σ1=t1t2和σ2=t1t3,代價分別為C(σ1)=2 和C(σ2)=3。由C(σ1) 由圖1 中的Petri 網實例可知,標注序列ω=a b對應的最小代價變遷發生序列為σ1=t1t2,標注序列ω=a b c對應的最小代價變遷發生序列為σ2=t1t3t5,即標注序列ω=a b c前兩個標注對應的最小代價變遷發生序列將被替代。當標注序列發生改變時,其對應的最小代價變遷發生序列也可能發生改變,因此需要計算每條搜索路徑中變遷發生序列的總代價。 復雜問題通常有較多的可行解,它們構成了問題的解空間。若沒有確定正確的解空間就開始搜索,可能會產生較多滿足約束條件的重復可行解或者錯誤解。解空間用如圖2 所示的解空間樹來表示。根節點作為初始狀態位于解空間樹的第一層,根據不同的約束條件對根節點做出選擇后得到的葉子節點位于第二層。以此類推,解空間樹的一個可行解為從樹的根節點到葉子節點的路徑[17]。 Fig.2 Model of solution-space tree圖2 解空間樹模型 基于回溯法估計標注Petri 網的最小代價計劃序列,剔除其他路徑中不滿足約束條件的標識,而非直接剪掉一條路徑。設lc是當前最小總代價,當搜索到一個標識M后,滿足,存在以下兩種情況: (1)若C(σ)≤lc,則該標識是構成搜索路徑的部分解,且繼續搜索下一個標識。 (2)若C(σ)>lc,則該標識不是構成搜索路徑的部分解,結束該路徑的搜索。 在圖3 所示的標識路徑搜索空間示意圖中,給定標注序列ω=l1l2…lk,假設成立,且C(t1) Fig.3 Schematic diagram of evolution of marking paths圖3 標識路徑演化示意圖 給定一個長度為k的標注序列ω=l1l2…lk(lj∈Σ,j=1,2,…,k),觀測到標注lj,j∈{1,2,…,k},集合Vj包含所有與標注lj相關的節點v。四元組節點v=(level,marking,sequence,cost),其中level為節點層次的序號;marking為節點相關標識;sequence為對應的變遷發生序列;cost為變遷序列的代價。若后繼需考慮節點v,則flag(v)=0;反之flag(v)=1。 算法1計算最小代價變遷序列 輸入:一個標注Petri 網Nl=(N,M0,Σ,L),一個長度為k的標注序列ω=l1l2…lk(lj∈Σ,j=1,2,…,k)。 輸出:包含所有最小代價變遷序列的集合S和最小代價lc。 觀測到標注lj,j∈{1,2,…,k},若標注lj對應多個變遷,則選擇代價較小的變遷優先發生。創建一個節點v之后,當v.cost≤lc時,若集合Vj中不存在節點v1,使得v1.marking=v.marking,則flag(v)=0,節點v進棧S,更新集合Vj=Vj∪{v};若集合Vj中存在節點v1,使得v1.marking=v.marking,則需考慮以下三種情況: (1)若v.cost (2)若v.cost>v1.cost,則flag(v)=1,節點v不進棧S; (3)若v.cost>v1.cost,則flag(v)=0,節點v進棧S,更新集合Vj=Vj∪{v}。 當j=k時,若v.cost 算法1 首先通過棧S獲得節點?,根據棧的性質,可以直接得到代價較小的變遷,避免發生代價較大的變遷。其次,通過比較發生節點變遷代價的大小,能夠確保該節點通過最小代價變遷發生獲得。最后,能夠避免在搜索路徑中出現大于當前最小總代價的變遷序列,從而使得算法1 能夠避免無效搜索,減少搜索的節點數目。 以圖4 所示文獻[14]中的一個包含兩臺并聯機器的制造系統標注Petri 網模型為例,標注集Σ={a,b,c,d,e,f,g,h} ;庫所集P={p1,p2,…,p10} ;變遷集T={t1,t2,…,t12} ;初始標識為M0=[1 1 0 2 0 0 2 0 0 0]T;標注函數為L(t3)=L(t5)=a,L(t4)=L(t6)=b,L(t7)=L(t9)=c,L(t8)=L(t10)=d,L(t1)=e,L(t2)=f,L(t11)=g,L(t12)=h;變遷代價為C(t1)=C(t2)=C(t4)=C(t5)=C(t9)=5,C(t3)=C(t7)=C(t8)=C(t10)=10,C(t6)=C(t11)=C(t12)=15。 Fig.4 Labeled Petri net model for manufacturing system圖4 一個制造系統的標注Petri網模型 給定長度為10 的標注序列ω=e e f f a a b c c d,根據這個序列,可得圖5 所示的Petri網模型的標識解空間示意圖。應用算法1,基于回溯法求取最小代價計劃序列的標識路徑搜索空間如圖6 所示。表1 總結了每條標識路徑中變遷發生的信息,每條路徑的標識序列和標識剔除情況如表2 所示。在圖6 所示的標識路徑搜索空間中,路徑①的標識集合Z(ω)={M1,M2,M3,M4,M51,M61,M71,M81,M91,M10},最小代價為lc=55。圖5 所示的標識解空間中存在多條路徑,回溯至祖先標識M51并搜索路徑②。路徑②的標識集合為Z(ω)={M1,M2,M3,M4,M51,M62,M72,M82,M91,M10},當變遷發生序列為σ2=t1t1t2t2t5t3t4t9t7時,C(σ2)=55,若繼續發生變遷t8,則C(σ2)=65,由于C(σ2)>lc,標注d對應的變遷t8不應發生,此時剔除標識M10。以同樣的方式搜索剩余路徑,獲得最小代價變遷序列集合S={t1t1t2t2t5t5t4t9t9t8},最小代價為lc=55。 Table 1 Information about firing of transitions in marking paths表1 標識路徑上的變遷發生信息 Fig.5 Marking solution space established according to labeled sequence ω=eeffa a b ccd圖5 根據標注序列ω=eeffa a b ccd 構建的標識解空間 Table 2 Marking sequences and the number of eliminated markings表2 標識序列與標識剔除數目 在上述包含兩臺并聯機器的制造系統標注Petri網模型中,基于回溯法與動態規劃法構建的標識解空間規模相同,因此僅給出基于回溯法構建的標識解空間。在標識路徑搜索空間中不合并相同的標識,由表2 可知,應用回溯法搜索的標識數目比應用動態規劃法搜索的標識數目減少約17%。對于給定的標注序列ω=e e f f a a b c c d,當觀測到的標注序列長度小于等于4 時,標注e和f僅對應一個變遷,即只存在一條搜索路徑,因此應用回溯法與動態規劃法搜索的標識數目相同;當標注序列長度大于4時,可以剔除路徑中不滿足約束條件的標識,合并相同的標識后,回溯法比動態規劃法減少搜索的標識數目由表3 給出。根據兩種方法處理該實例的結果可知,基于回溯法估計標注Petri 網的最小代價計劃序列可以減少計算量。 本文提出一種方法,基于回溯法估計標注Petri網的最小代價計劃序列。雖然沒有從理論上降低蠻力窮舉方法與文獻[14]所提方法的計算復雜度,但是本文方法在搜索標識的過程中,通過深度優先策略可以避免不滿足約束條件的變遷發生,從而減少了搜索的標識數目,提高了工作效率。 Fig.6 Searching-space of marking paths圖6 標識路徑搜索空間 Table 3 Comparative analysis of number of markings表3 標識數目對比分析 本文研究制造系統標注Petri 網模型的最小代價計劃序列估計問題,提出了一種基于回溯法求取最小代價變遷序列的算法。根據深度優先搜索策略可以獲得標注Petri 網的一個當前最小代價變遷序列,以該序列的代價作為其他路徑搜索部分解的約束條件,滿足約束條件的一條完整路徑即對應問題的一個解。實例結果表明,本文算法能夠剔除冗余標識,縮小搜索空間規模,提高工作效率。后續工作將結合本文方法,在含有不可觀測變遷的標注Petri 網中估計最小代價計劃序列。2 基于回溯法求取最小代價變遷序列
2.1 解空間樹的構建
2.2 最小代價變遷序列的獲取
2.3 算法
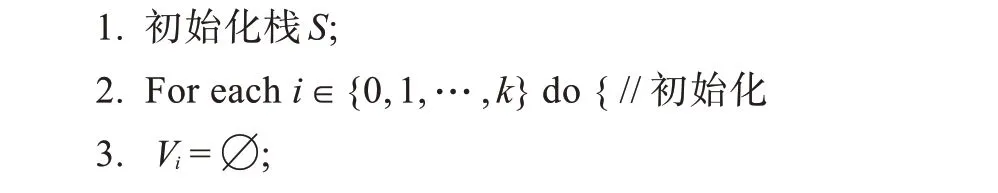


3 應用實例與結果分析
3.1 應用實例


3.2 結果分析
4 結束語

