渤海灣M2 分潮的季節變化：增強調和分析的應用

余鷹，王道勝,2*

( 1. 中國地質大學（武漢） 海洋學院 海洋地質資源湖北省重點實驗室，湖北 武漢 430074；2. 中國地質大學 深圳研究院，廣東 深圳 518057)

1 引言

由于海洋物理性質和海岸形態的變化，潮汐存在多個時間尺度的變化[1]，尤其是沿海和極地地區的M2分潮[2]。前人研究表明，英國海岸[3]、西北歐大陸架[4]、黃海和東海[5]、哈得孫河口[6]和東南亞海岸[1]等沿海地區，M2分潮都存在著季節變化。此外，相關研究表明極地地區M2分潮也存在季節變化[2,7-8]。

為了分析M2分潮的季節變化，傳統上將觀測的水位數據分段，并對每一段進行經典調和分析（Classical Harmonic Analysis, CHA），該方法可以通過MATLAB 中的T_TIDE 工具包來實現[9]。上述過程稱為分段調和分析（Segmented Harmonic Analysis, SHA），該方法在前人研究中得到廣泛使用[2,5,10-13]。當直接使用SHA 時，得到的振幅和遲角是離散的，需要對其進行插值以得到連續的結果。如果采用時間窗滑動的方式，一些峰值和快速變化的信號會被平滑，若某些分段中存在較多缺測，則可能導致計算結果不準確。除此之外，在使用SHA 進行月度分析時，一些無法分辨的潮汐成分也需謹慎處理。Jin 等[10]提出了增強調和分析（Enhanced Harmonic Analysis, EHA）方法，可以直接得到內潮不同潮汐成分時變的振幅和遲角。Pan等[14]基于EHA 方法開發了S_TIDE 工具包，并利用S_TIDE 研究了哥倫比亞河口的潮汐-河流相互作用。根據Pan 等[14]所述，在S_TIDE 中如何針對分析的潮汐成分選擇合適的獨立點數是一項相對復雜的工作，應通過一系列敏感性試驗來測試，以避免產生虛假的結果。

在SHA 和EHA 中，所有潮汐成分的調和常數均被認為是隨時間變化的。然而，潮汐季節變化的原因錯綜復雜[15]，在大多數情況下，只有主要分潮（如M2分潮）的時間變化是顯著并需要關注的，而其他分潮的時間變化比較微弱且可以忽略不計。EHA 認為所有分潮的振幅和遲角都是隨時間變化的，一方面增加了計算的復雜度和需要的計算機內存，另一方面顯著減少了能夠分辨的分潮數量。Wang 等[16]對EHA 進行了改進，使其不僅能得到主要分潮時變的振幅和遲角，同時也能得到其他分潮不變的振幅和遲角。為便于對EHA 改進前后的效果進行對比分析，改進前的EHA，即：假定所有潮汐成分的調和常數均隨時間變化的EHA，被記為OEHA（Original EHA），而改進后的EHA 則簡記為EHA。本文使用渤海灣的水位觀測數據，通過設計理想實驗，構建人造“水位數據”驗證EHA 的可行性和有效性，并利用EHA 得到了渤海灣M2分潮振幅的季節變化，同時討論了渤海灣M2分潮振幅季節變化的原因。

2 方法與數據

2.1 EHA

海平面高度由多個因素決定，可表達為[16-18]

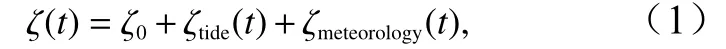
式中， ζ(t)代表海平面高度(即：水位)，右邊3 項分別是平均海平面高度(Mean Sea Level, MSL)、潮汐引起的海表面高度、氣象因素導致的海表面高度。在不考慮節點調制的情況下，潮汐的計算通常是k個分潮之和，即

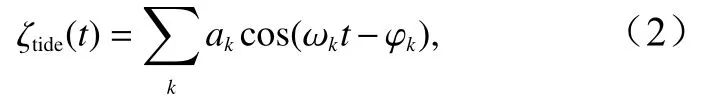
式中， ω，a和φ分別代表每個分潮的角速度（單位：rad/s），振幅（單位：m）和遲角（單位：rad）。在OEHA 中， ζ0，a和φ均被認為是隨時間變化的[10,14]，即

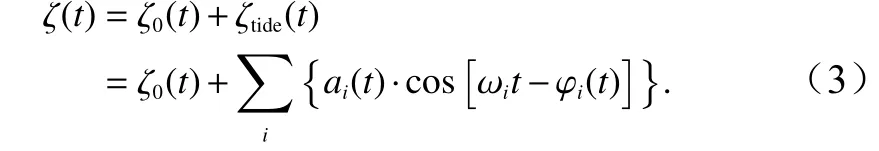
在OEHA 的基礎上，Wang 等[16]進行了改進。在改進后的EHA 中，只有幾個主要分潮的振幅和遲角是時變的，而其他分潮的振幅和遲角仍然是常數[16]。因此，海平面高度的表達式為

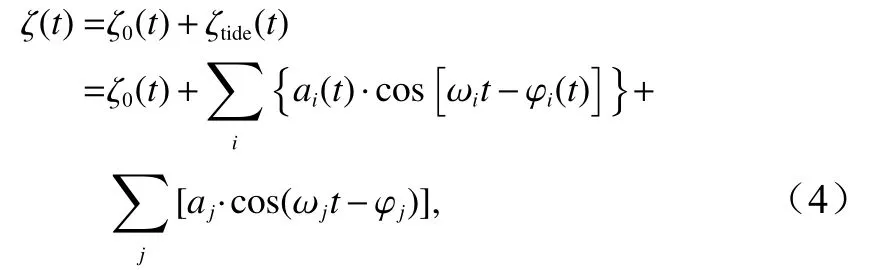
式中，具有時變振幅和遲角的分潮數量為i, 而振幅和遲角是常數的分潮數量為j，ζ0(t)包含氣象因素導致的海表面高度[16]。類似于Jin 等[10]和Pan 等[14]，改進后的EHA 在求解時變的平均海平面高度、振幅和遲角時，引入了獨立點方案和三次樣條插值法，而上述的時變量和等號右邊第三項中的常數振幅和遲角可以用最小二乘法同時求解。此外，誤差評估算法與Jin 等[10]和Pan 等[14]相同。改進后的EHA 已更新到S_TIDE 中， 可以從以下網站獲取： https://www.researchgate.net/project/A-non-stationary-tidal-analysistoolbox-S-TIDE。

2.2 數據來源

本文采用的數據是中國渤海灣的兩個站點E1 和E2 的逐時水位數據(已減去平均水位)，觀測數據的時間跨度為2013 年11 月1 日(世界時，下同)到2014 年11 月1 日，圖1 標注了E1 和E2 站點的位置。如圖2所示，E1 站點有大約1/4 的數據缺測，而E2 站點的數據是連續的，E1 和E2 的海平面振幅大多小于2 m。

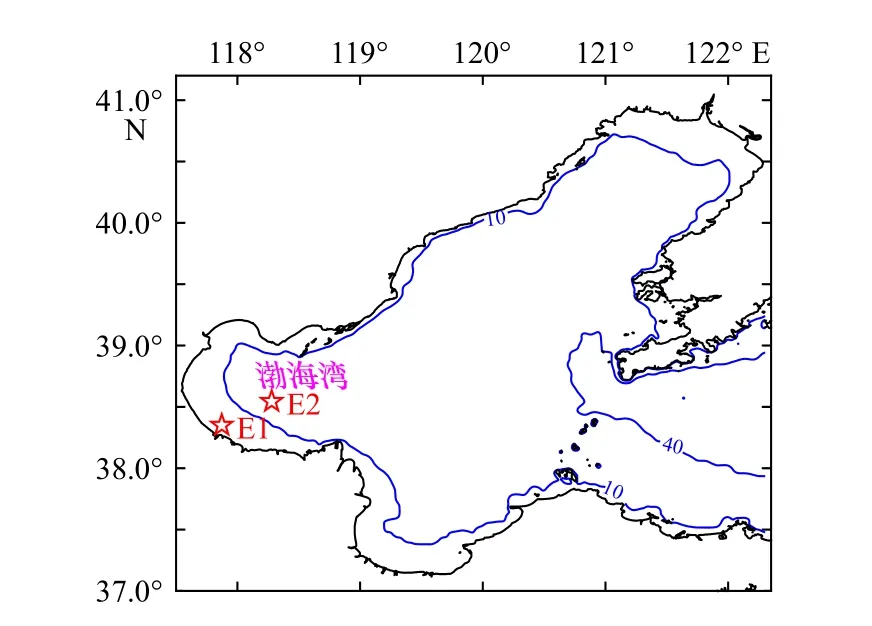
圖1 渤海灣觀測站E1 和E2 的位置（紅星），以及10 m 和40 m 水深線Fig. 1 The locations of the observation stations (E1 and E2,red stars) in the Bohai Bay, and the isobathymetric lines at 10 m and 40 m

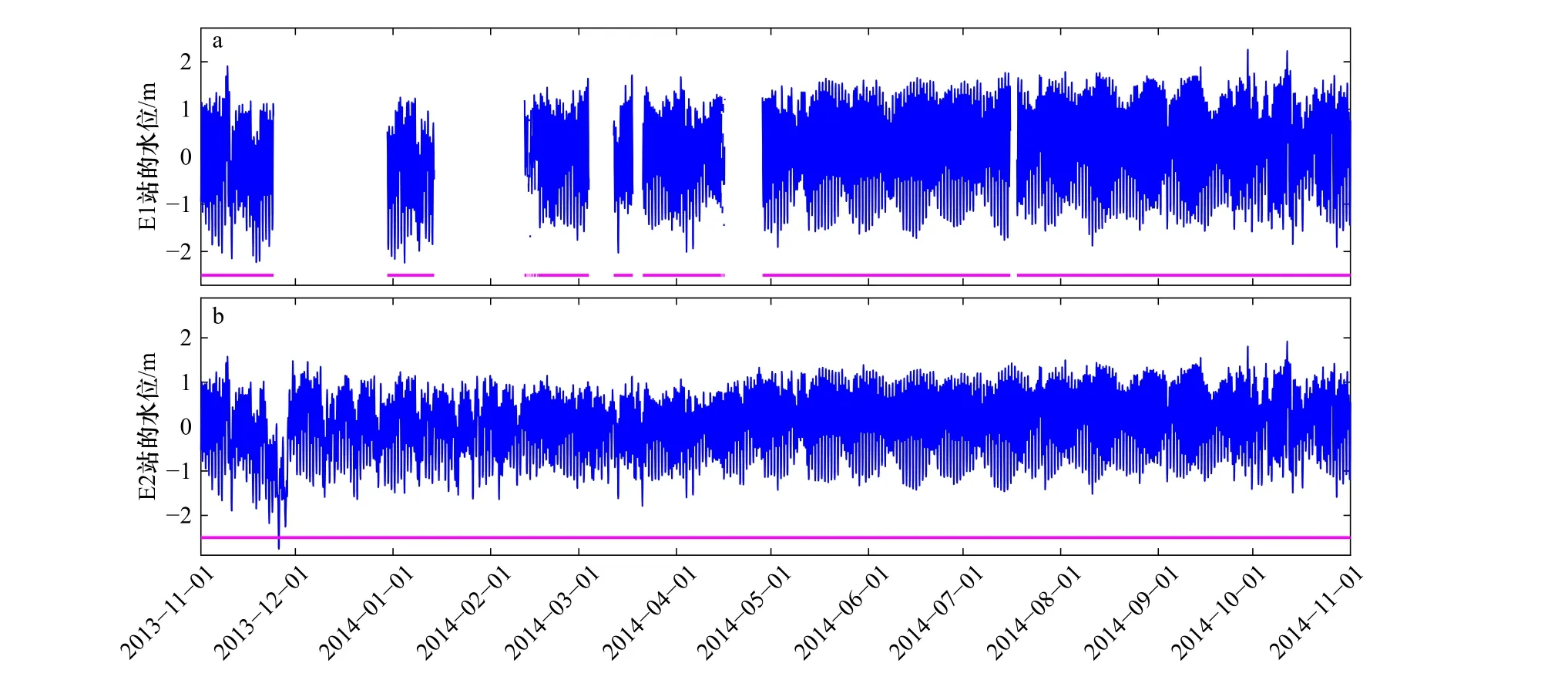
圖2 E1（a）和E2（b）站的水位觀測數據Fig. 2 The observed sea level at E1(a) and E2(b) stations

2.3 EHA 的驗證

在分析實際水位數據時，分潮振幅和遲角的真實值并不清楚，無法驗證方法的準確性。因此，本文首先通過理想實驗來驗證EHA 方法的可行性和有效性。

2.3.1 人造“水位數據”

根據E2 站的水位數據來構造理想實驗中的人造“水位數據”。圖3 呈現了E2 站點水位數據的功率譜密度，很明顯，水位的波動主要受半日潮(如M2和S2)影響；同時，M2分潮的能量最強，全日潮(如K1和O1)也很顯著。由于半日潮和全日潮的非線性相互作用和平流作用[19]，MK3和M4分潮的頻率同樣出現譜峰。低頻部分也出現了一些譜峰，不失一般性，選擇0.235 cpd和0.392 cpd 兩個頻段的水位信號作為低頻代表，分別標記為LF1 和LF2。

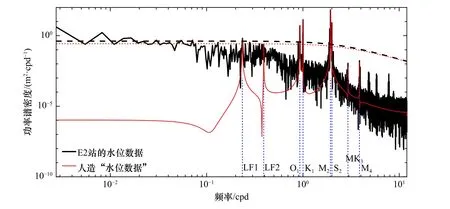
圖3 E2 站水位數據和人造“水位數據”的功率譜密度Fig. 3 The power spectral densities of the observed sea level at E2 Station and the artificial sea level

假定MSL 為0，故人造“水位數據”將由潮頻信號(包括M2、S2、K1、O1、MK3和M4)和低頻信號(包括LF1 和LF2)組成，如下式所示：

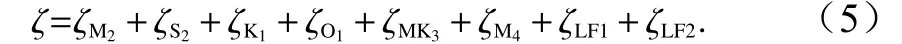
在人造“水位數據”中，假設M2分潮的振幅和遲角是隨時間變化的，而其他信號的振幅和遲角均是常數。另外，MK3、M4、LF1 和LF2 被視為噪聲，不估計其振幅和遲角。為了獲得M2分潮振幅和遲角較為真實的時間變化，在不考慮節點調制的情況下，通過SHA分析了E2 的真實水位數據，如圖4 所示。結果表明，M2分潮的振幅和遲角存在明顯的時間變化。為了獲得更加平滑的時間變化特征，利用正弦函數對SHA方法所得M2分潮振幅和遲角進行了擬合。圖4 中的紅線展示了擬合結果，擬合公式如下：

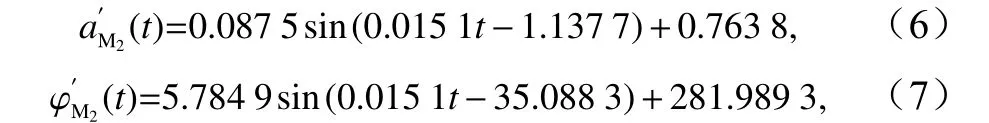
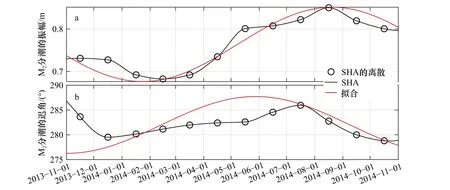
圖4 使用SHA 分析E2 站水位觀測數據所獲得M2 分潮時變的振幅(a)和遲角(b)及其擬合值Fig. 4 The temporally varying amplitude (a) and phase lag (b) of the M2 constituent obtained by analyzing the observed sea level at E2 Station using SHA and their fitting values

式中，t表示從世界時0 年1 月0 日起經過的時間（即MATLAB 中的“datenum”值），單位：d；此外，t的范圍為2013 年11 月1 日至2014 年11 月1 日，與E2 站實際水位觀測數據的時間范圍相同；a′M2是M2分潮的時變振幅，單位：m； φ′M2為M2分潮的時變遲角，單位：（°）。參考CHA[9]，由M2分潮引起的水位變化的表達式為下

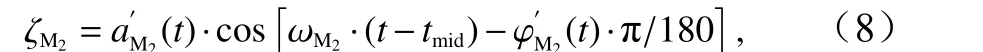
式中，tmid是t的中值。

為了獲得其他潮汐信號較為真實的振幅和遲角，在不考慮節點調制的情況下，使用CHA 分析了E2 處的海平面數據，得到的常數形式的振幅和遲角如表1所示。LF1 和LF2 的遲角設置為4 個主要分潮的平均遲角，并根據功率譜密度的結果，通過反復試驗得到了振幅值，見表1。由上述信號引起的水位變化與M2分潮引起的水位變化具有類似的形式(即式(8))，此處不再贅述。

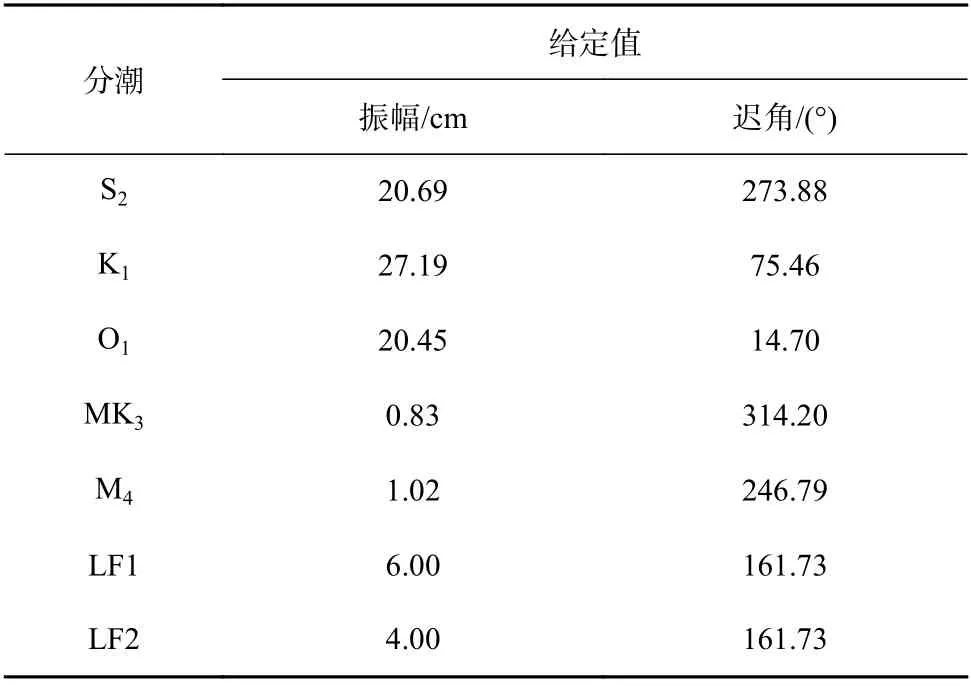
表1 理想實驗中的潮汐成分及其常數形式的振幅和遲角Table 1 The prescribed constant amplitudes and phase lags of the constituents in ideal twin experiments

從人造“水位數據”的功率譜密度（圖3）可以看出，人造“水位數據”成功地再現了E2 站M2、S2、K1、O1、MK3、M4、LF1、LF2 等信號，且不包含其他頻段的信號，表明由已知的振幅和遲角構造的“水位數據”可以作為E2 站真實水位觀測數據的替代品。

2.3.2 實驗和結果

在理想實驗中，不考慮節點調制，采用CHA、SHA、OEHA 和EHA 分析人造“水位數據”，以獲得M2、S2、K1和O14 個主要分潮的振幅和遲角，除此之外，人造“水位數據”中的其他信號，被視作噪聲[20]。在使用SHA 時，每個月的數據作為一段進行分析，根據瑞利準則，區分上述4 個主要分潮的最小周期為14.8 d[21]，因此，只有當該段數據長度大于15 d 時，SHA 才對該段數據進行分析。此外，采用3 次樣條插值法對每段所得離散的振幅和遲角進行插值以獲得連續的結果。Pan 等[14]指出，在不同獨立點數下，EHA 得到的時變振幅和遲角代表了不同時間尺度上的變化。根據Jin 等[10]的研究結果，在下面的理想實驗中，OEHA和EHA 的獨立點數被設為5，比季節數（春、夏、秋、冬）多1。

如圖5 所示，SHA、OEHA 和EHA 得到的M2分潮時變的振幅和遲角幾乎等于給定值；CHA 得到的結果是恒定的，不能捕捉到M2分潮的時間變化，而SHA、OEHA 和EHA 可以得到M2分潮的時間變化特征。

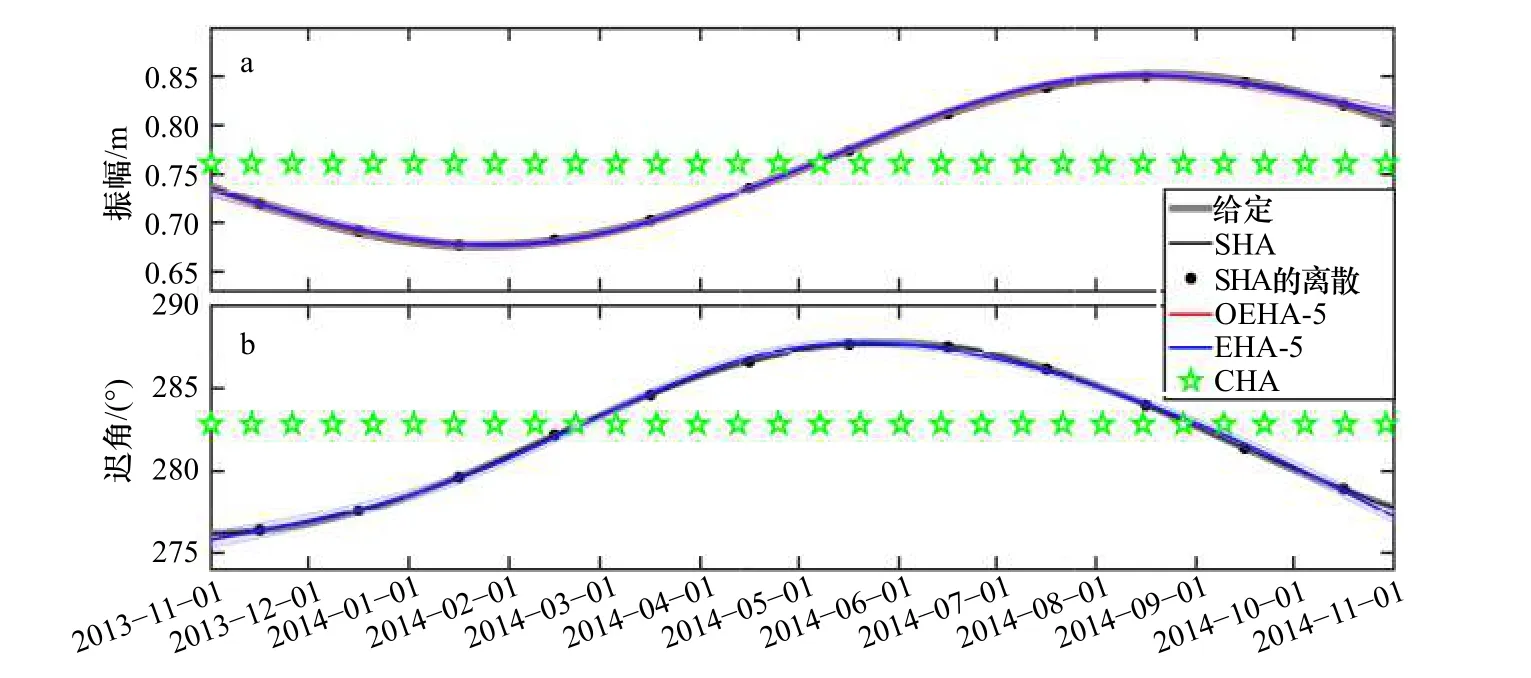
圖5 理想實驗中給定的M2 分潮振幅（a）和遲角（b），以及使用SHA、采用5 個獨立點的OEHA、采用5 個獨立點的EHA 和CHA 得到的結果Fig. 5 The amplitude (a) and phase lag (b) of the M2 constituent prescribed in ideal experiments and the estimated values using SHA,OEHA with 5 independent points, EHA with 5 independent points, and CHA

對于S2分潮而言，EHA 分析所得振幅和遲角比CHA 所得結果更接近給定值（圖6a 和圖6b），而SHA的結果與給定值相差甚遠，尤其是遲角（圖6b），這主要是因為M2分潮和S2分潮的頻率很接近，當同時被假定為隨時間變化時，分析結果可能會互相影響。使用OEHA 時，除2014 年10 月和11 月外，S2分潮的遲角幾乎都等于給定值；此外，得到的S2分潮的振幅是時變的，與給定值有一定的偏差。對于K1分潮（圖6c和圖6d）和O1分潮（圖6e 和圖6f），CHA 和EHA 所得結果幾乎等于給定值，而OEHA 得到的振幅和遲角整體上接近給定值，但在端點處差距較大，SHA 分析所得振幅和遲角具有明顯的時間變化特征，與給定值相差較大。總的來說，雖然SHA、OEHA 和EHA 均能成功估計M2分潮的時間變化特征，但EHA 所得其他3 個主要分潮的振幅和遲角與給定值吻合最好。

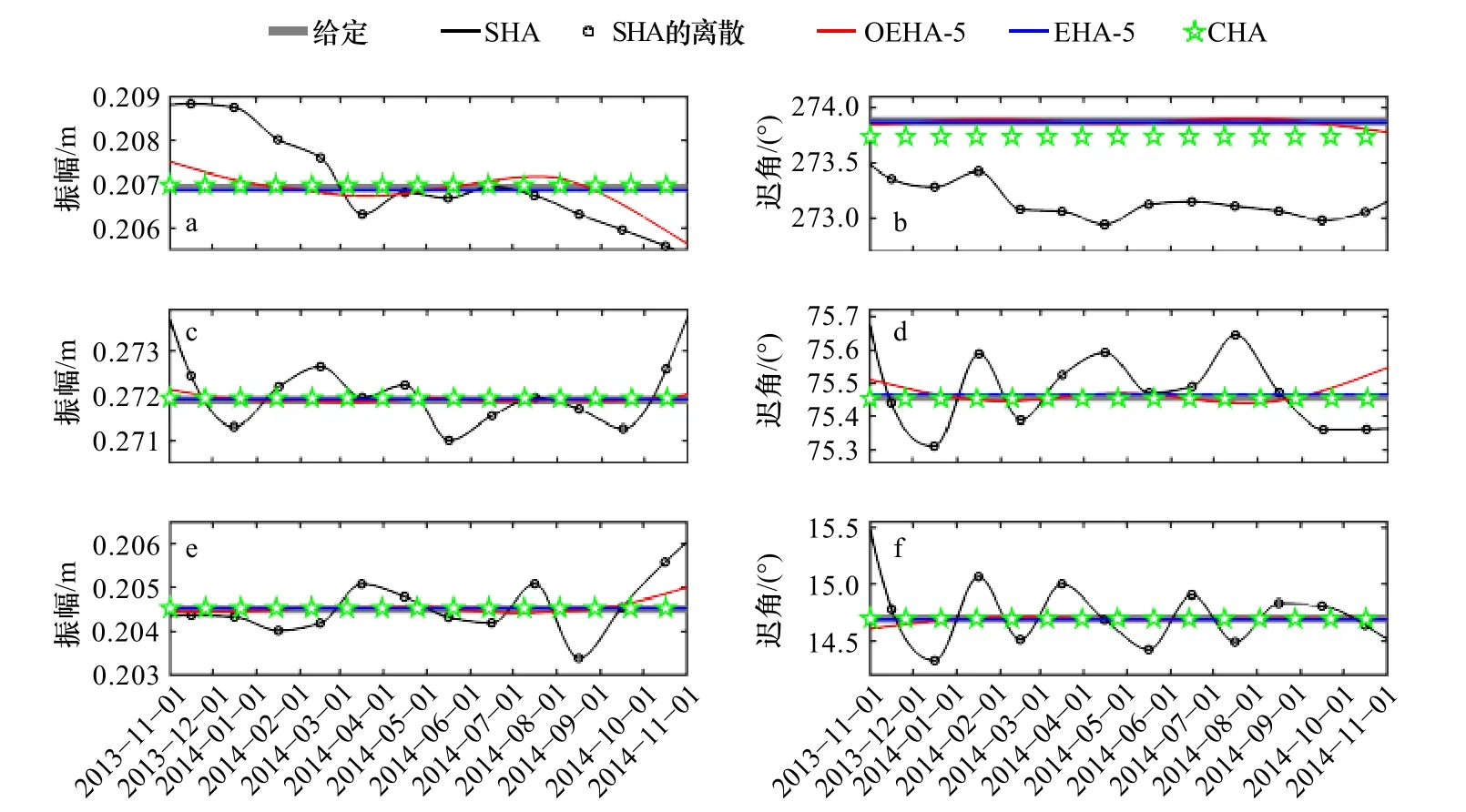
圖6 理想實驗中給定的S2 分潮（a，b）、K1 分潮（c，d）和O1 分潮（e，f）的振幅和遲角，以及使用SHA、采用5 個獨立點的OEHA、采用5 個獨立點的EHA 和CHA 得到的結果Fig. 6 The amplitude and phase lag of the S2 (a, b), K1 (c, d) and O1 (e, f) constituent prescribed in ideal experiments and the estimated values using SHA, OEHA with 5 independent points, EHA with 5 independent points, and CHA

需要注意的是，E1 站的實際水位觀測數據存在部分缺測，這可能會對分析結果造成影響。在理想敏感實驗中，根據E1 站的缺測時段，剔除了人造“水位數據”中相應的數據，進而利用CHA、SHA、OEHA、EHA 對其進行了分析。雖然大約1/4 的時段沒有“水位數據”，但是OEHA 和EHA 所得結果很好地捕獲了M2分潮給定振幅和遲角的時間變化特征（圖7a和圖7b）。相反，SHA 所得M2分潮的振幅和遲角與給定值略有偏差，特別是在2013 年11 月至2014 年2 月期間，這主要是因為2013 年12 月和2014 年1 月的缺測較多，導致這兩個月的“水位數據”沒有被分析而無法獲得M2分潮振幅和遲角值。EHA 分析得到的M2分潮所引起的水位變化與給定的M2分潮所導致的水位變化之間的絕均差為0.19 cm；而SHA 所得絕均差為0.28 cm，約為沒有缺測時的4.5 倍。對于S2、K1和O1分潮，CHA 分析所得振幅和遲角值與給定值之間的差距比理想實驗中的差距更大，如圖8所示；此外，“水位數據”的缺測對SHA 和OEHA 的結果也有很大的影響，OEHA 分析所得3 個分潮的振幅和遲角與給定值之間的誤差變得更大。相反，EHA得到的S2和K1分潮的振幅和遲角仍然接近給定值。雖然EHA 對O1分潮的分析結果與給定值略有偏差，但差異明顯小于CHA、SHA 和OEHA 的結果。由此可見，EHA 總體上優于CHA、SHA 和OEHA。

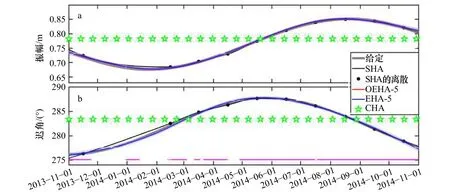
圖7 理想敏感實驗中給定的M2 分潮振幅（a）和遲角（b），以及使用SHA、采用5 個獨立點的OEHA、采用5 個獨立點的EHA 和CHA 得到的結果Fig. 7 The amplitude (a) and phase lag (b) of the M2 constituent prescribed in ideal sensitivity experiments and the estimated values using SHA, OEHA with 5 independent points, EHA with 5 independent points, and CHA

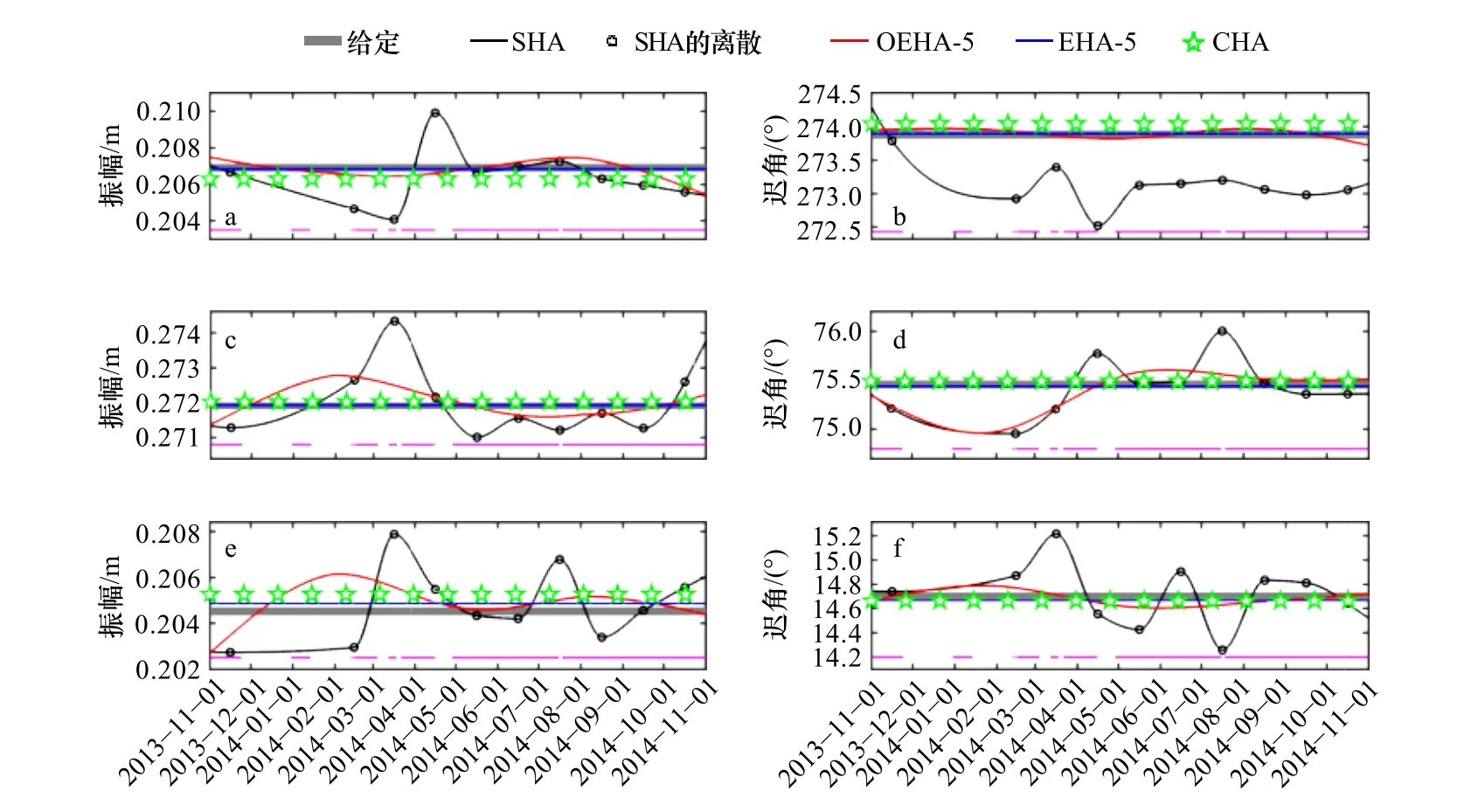
圖8 理想敏感實驗中給定的S2 分潮（a, b）、K1 分潮（c, d）和O1 分潮（e, f）的振幅和遲角，以及使用SHA、采用5 個獨立點的OEHA、采用5 個獨立點的EHA 和CHA 得到的結果Fig. 8 The amplitude and phase lag of the S2 (a, b), K1 (c, d) and O1 (e, f) constituent prescribed in ideal sensitivity experiments and the estimated values using SHA, OEHA with 5 independent points, EHA with 5 independent points, and CHA

總體而言，無論“水位數據”中是否存在缺測，在利用EHA 進行分析時，M2分潮時變振幅和遲角以及其他分潮調和常數的給定值都能被準確反演，說明EHA 能有效分離具有不同變化特征的潮汐信號，可用于實際實驗中M2分潮的季節變化研究。

3 EHA 在渤海灣M2 分潮季節變化研究中的應用

3.1 基準實驗

為了確定基準實驗中所需分析的潮汐成分，利用CHA 對E1 和E2 站的水位觀測數據進行了調和分析，根據信噪比的大小[9,22]選擇了M2、K1、S2和O14 個最重要的成分作為進行分析的分潮。利用EHA進行數據分析時，獨立點數設置為5，僅將M2分潮的振幅和遲角假定為隨時間變化。

CHA 和EHA 所得E2 站M2分潮振幅的分析結果如圖9b 所示。從圖中可以看出，EHA 分析所得M2分潮振幅具有明顯的季節變化特征，其平均值與CHA分析所得常數形式的M2分潮振幅幾乎相等，說明了EHA 所得分析結果的合理性。

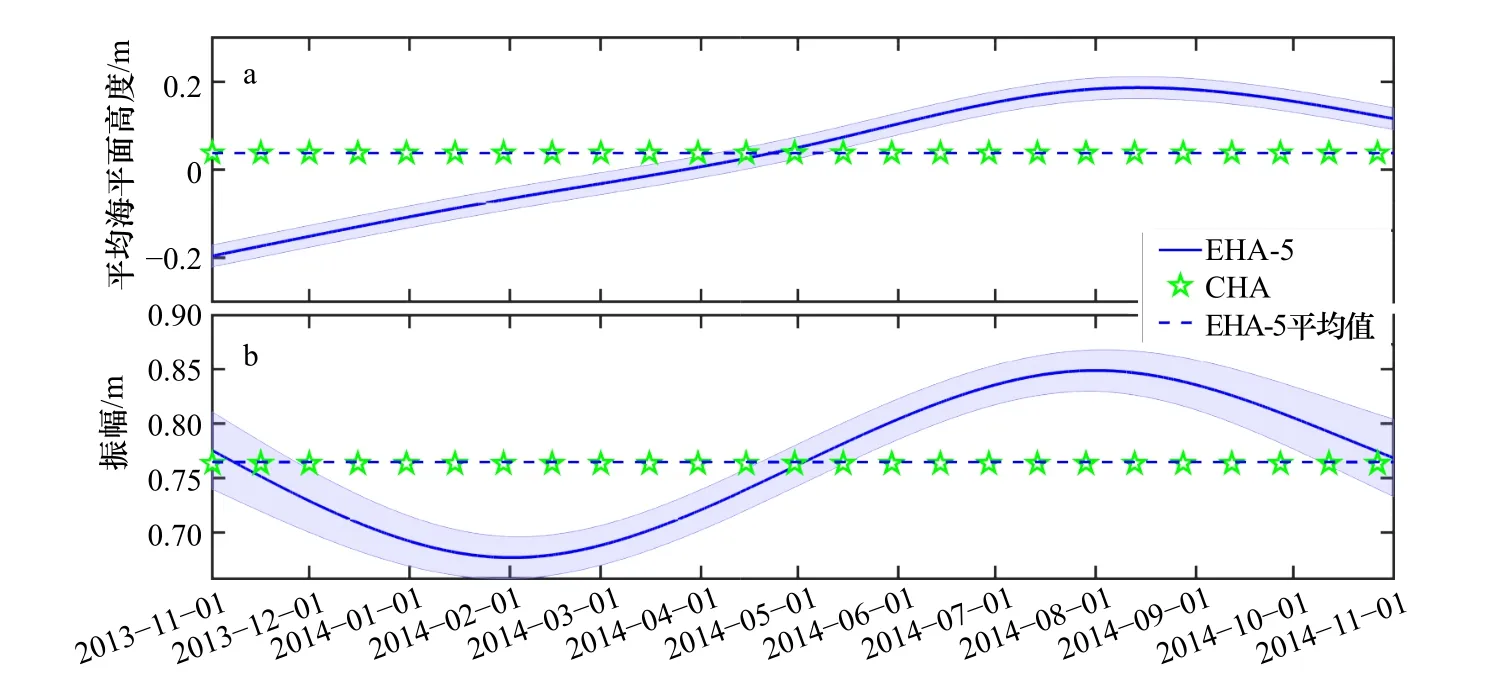
圖9 E2 站基準實驗的實驗結果Fig. 9 The results of benchmark experiment at E2 Station

EHA 所得隨時間變化的M2振幅在夏季（大約7-8 月）達到最大值，在冬季（大約1-2 月）達到最小值，夏季M2分潮振幅比年平均值大8.42 cm（約11.01%），而冬季值比年平均值小8.76 cm（約11.46%），其季節變化幅度遠大于在觀測期內由18.6 a 的節點調制引起的振幅變化（不超過1%）。表2 列出了CHA 和EHA在E2 站分析所得其他分潮的振幅值，可以看出，EHA和CHA 分析所得其他3 個主要分潮的常數形式的振幅值之間的絕均差最大僅為0.07 cm，進一步表明EHA 不僅可以準確提取M2分潮振幅的季節變化特征，也能準確得到其他分潮的常數形式的振幅。

CHA 和EHA 分析所得E2 站MSL 如圖9a 所示。可以看出，EHA 分析所得隨時間變化的MSL 的平均值幾乎等于CHA 分析所得常數形式的MSL，進一步表明EHA 的結果是合理的。但是需要注意的是，EHA分析所得E2 站處MSL 在1 年內的變化約為0.4 m，遠大于傳統上MSL 的全球平均變化（約為0.001 m/a）[23-24]，這主要是因為EHA 中隨時間變化的MSL 包含氣象因素導致的水位變化（式（3））。如Lü等[18]所述，風速和氣壓等氣象因素均會影響到低頻水位的變化，因此包含了氣象因素影響的MSL 在2013 年11 月和2014 年11 月存在一定的差異，該現象在E1 站同樣存在。EHA分析所得時變MSL 的最大值出現在夏季，而最小值出現在冬季。與M2分潮振幅的時間變化特征相似，EHA 分析所得MSL 的時間變化比較平穩，且不存在季節變化之外的信號。

CHA 和EHA 分析所得E1 站MSL 和M2分潮振幅的結果如圖10 所示。可以看出，EHA 分析所得隨時間變化的M2分潮振幅比較平滑，且與E2 站具有相同的變化趨勢。在夏季，M2分潮振幅增加了約6.05%，而在冬季則減少了3.85%，這比在觀測期內由18.6 a節點調制引起的不超過1%的振幅變化大得多。從表2 中可以看出，EHA 分析所得其他3 個分潮的常數形式的振幅與CHA 分析所得結果非常接近。此外，EHA 分析所得隨時間變化的MSL 在夏季達到最大值，在冬季達到最小值，與E1 站M2分潮的季節變化特征相同。需要注意的是，E1 站和E2 站相距較近，但對比圖9a 和圖10a 發現，E1 站和E2 站的平均海平面的年變化并不完全一致，E2 站MSL 的最小值出現在11 月，而E1 站MSL 的最小值出現在1 月，這是由于E1 站2014年1 月和2 月的數據存在缺測，會給該時間段的平均海平面的計算帶來偏差，從而影響最小MSL 出現的月份，但并沒有顯著影響兩站的M2分潮振幅和MSL 的變化趨勢，表明EHA 在即使存在缺測的E1 站，也可以得到相對合理的結果。

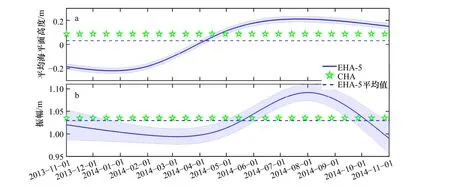
圖10 E1 站基準實驗的實驗結果Fig. 10 The results of benchmark experiment at E1 Station

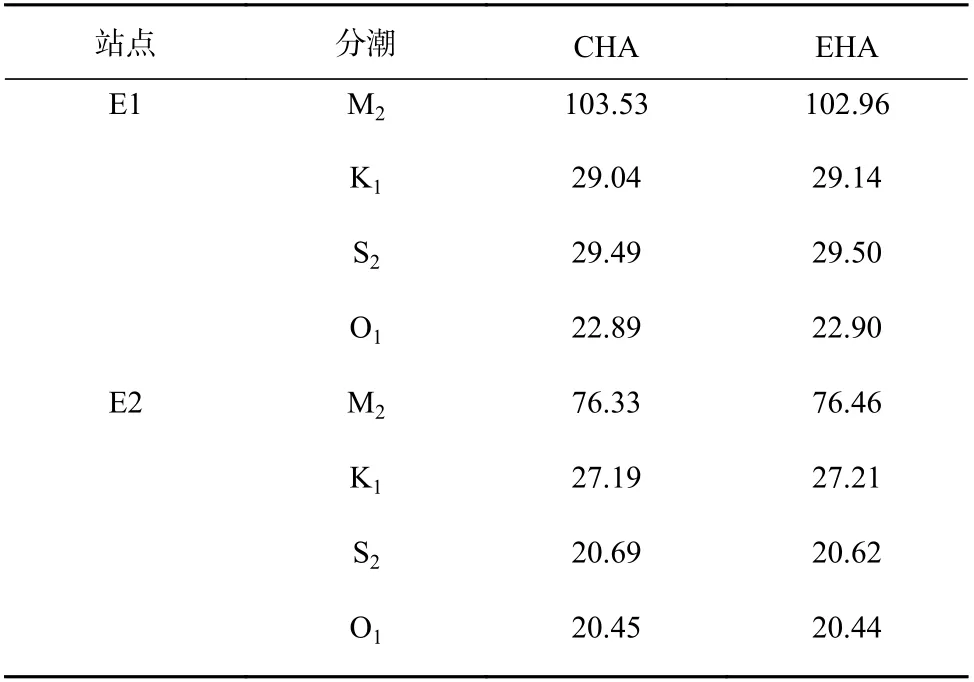
表2 基準實驗中CHA 和EHA 分析所得4 個主要分潮的振幅（單位：cm）Table 2 The amplitudes of four main tidal constituents obtained by CHA and EHA in the benchmark experiment (unit:cm)

綜上所述，EHA 在E1 站和E2 站分析所得M2分潮振幅具有相同的季節變化特征：夏季大，冬季小。E2站M2分潮振幅的相對變化約為11%，在E1 站約為5%，這與Foreman 等[11]、Huess 和Andersen[4]的結果（6%），以及Müller 等[2]根據模型和觀測數據所分析的結果（5%～10%）相近。此外，EHA 在E1 站和E2 站分析所得時變MSL 具有與M2分潮振幅相同的季節性變化，這表明MSL 可能是導致M2分潮振幅季節變化的因素之一，因為潮波的傳播受到水深的影響[13]。

3.2 對分潮選擇的敏感性實驗

在基準實驗中，選擇了4 個主要分潮進行評估，并且假定只有M2分潮的振幅和遲角隨時間變化。當其他分潮也被分析或其他分潮振幅和遲角也被假定為隨時間變化時，M2分潮的分析結果可能會受到影響。因此，對E2 站的數據進行了一些新的實驗來測試EHA 分析所得的M2分潮振幅季節變化特征對分潮選擇的敏感性。如表3 所示，在敏感性實驗SE11-SE13中，對M2，K1，S2和O14 個分潮進行分析，這與基準實驗相同，但具有時變振幅和遲角的分潮不同；在敏感性實驗SE21-SE24 中，與基準實驗不同的是，將對M2、K1、S2、O1、N2、K2、P1和Q18 個分潮進行分析，且振幅和遲角隨時間變化的分潮也發生了變化。

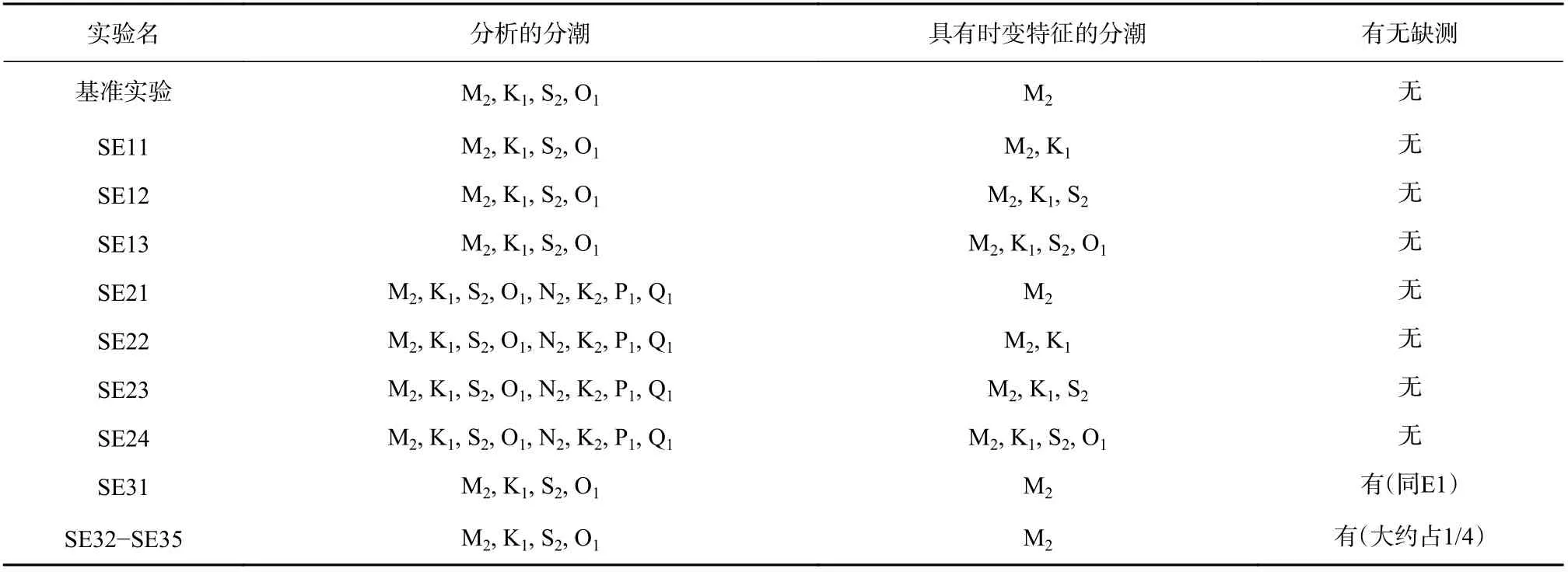
表3 實際實驗中的詳細實驗設置Table 3 The detailed experimental settings of the practical experiments

上述敏感性實驗中，EHA 分析所得隨時間變化的MSL 和M2分潮振幅如圖11 所示。可以看出，當具有時變特征的分潮發生改變時（SE11-SE13），EHA分析所得隨時間變化的M2分潮振幅和MSL 幾乎與基準實驗的結果完全一致。當分析的分潮數目發生變化時（SE21-SE24），EHA 分析所得隨時間變化的MSL與基準實驗的結果幾乎完全一致（圖11c）；此外，雖然隨時間變化的M2分潮振幅與基準實驗結果不完全相同，但整體變化趨勢是一致的（圖11d）。值得注意的是，SE21-SE24 中隨時間變化的M2分潮振幅幾乎彼此相等，這與SE11-SE13 所得結論一致。上述結果表明，EHA 中被分析的分潮和具有時變特征的分潮的選取并不會影響分析所得M2分潮振幅和MSL 的時間變化趨勢和季節變化特征。

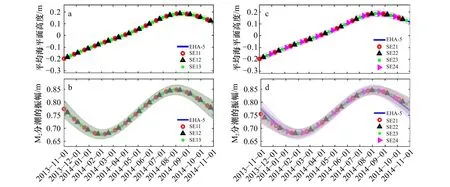
圖11 分潮選擇的敏感性實驗結果Fig. 11 The results on the sensitivity of tidal constituent selection

3.3 對數據缺失的敏感性實驗

時變M2分潮振幅和MSL 的分析結果也可能會受到數據缺測的影響。因此，利用E2 站的數據進行了一系列實驗以測試EHA 分析結果對數據缺測的敏感性。如表3 所示，在敏感性實驗SE31 中，根據E1 點缺測情況，相應地剔除了E2 站水位觀測數據。E1 站水位數據中存在大約1/4 的缺測，因此，為了進一步檢驗數據缺失的影響，將E2 站水位觀測數據平均分為4 份，并將這4 份水位觀測數據分別作為SE32-SE35中的缺測數據。其他實驗設置與基準實驗完全相同。

敏感性實驗SE31-SE35 的結果如圖12 所示。可以看出，由于SE31-SE35 的水位觀測數據存在約1/4 的數據缺失，因此EHA 分析所得M2分潮振幅和MSL 均與基準實驗中的值不完全相同。對比實驗SE31 和基準實驗中分析所得E2 站MSL 的結果，可以看到當E2 站數據在2014 年1 月和2014 年2 月出現缺測時，雖然MSL 的最小值出現的月份在2013 年11 月，但是這種現象并沒有數據無缺測時那么顯著，并且2013 年11 月至2014 年2 月的分析結果與無缺測時的分析結果存在明顯的差異，說明了數據缺失是導致E1 站和E2 站MSL 最小值出現月份不同的原因。但是，SE31-SE35 中所得M2分潮振幅和MSL 的變化趨勢與基準實驗中的相同：夏季大，冬季小。實驗結果表明，數據在某一月份的集中缺測會給該月的計算結果帶來影響，但不會顯著影響EHA 分析所得M2分潮振幅和MSL 的季節變化特征，并進一步論證了EHA所得E1 站的M2分潮振幅季節變化是合理、可信的。

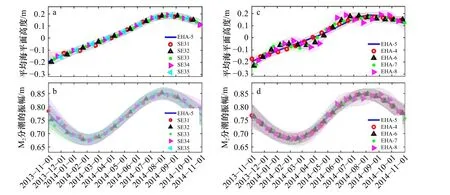
圖12 數據缺失和獨立點數的敏感性實驗結果Fig. 12 The results on the sensitivity of missing data and independent points

3.4 對獨立點數的敏感性實驗

Jin 等[10]指出，如何選擇EHA 中的獨立點是一個需要進一步研究的問題。而Pan 等[14]則指出，EHA在不同獨立點數時所得到的分析結果代表了不同時間尺度上的振蕩。同樣地，選擇合適的獨立點數對EHA 的表現也非常重要，尤其是對于E1 站非連續的水位數據。因此在新的敏感性實驗中嘗試了4 個、6 個、7 個和8 個等不同的獨立點數。

如圖12d 所示，當獨立點數取為季節數的兩倍（即：8）時，EHA 分析所得E2 站的M2 分潮振幅的時間變化趨勢與基準實驗結果一致，但存在除季節變化之外的震蕩，結果表明：EHA 中，獨立點越多并不一定會得到更真實的結果。

當獨立點數大于3 且小于8 時，EHA 分析所得M2振幅和MSL 的結果并不完全與5 個獨立點時的結果等同，但其季節性變化趨勢相同。如Pan 等[14]所述，不同獨立點數得到的結果不同，可能是因為采用不同獨立點數的EHA 得到的結果包含了不同的信號。以上所有敏感性實驗的結果表明：EHA 分析所得E2 站M2分潮振幅的季節變化特征是魯棒的，不受實驗設置的影響。

4 討論

平均海平面、層化和渦動黏性系數的季節變化是造成沿海地區M2分潮振幅呈現季節性變化的主要原因[4,13,15]。渤海灣的風場不僅對平均海平面有重大影響[18]，因受東亞季風影響而具有明顯的季節變化特征[25]。此外，季風還可以影響層化渦動黏性系數[26-29]。參照Devlin等[1]，采用北太平洋季風指數(WNPMI)來表征東亞季風[30]。WNPMI 下載網址為：http://apdrc.soest.hawaii.edu/projects/monsoon/daily-data.html#mon。如圖13 所示，WNPMI 與E1 站和E2 站M2分潮振幅具有顯著的正相關，相關系數分別為0.86 和0.87，表明：東亞季風可能是造成渤海灣M2分潮振幅季節性變化的內在原因。

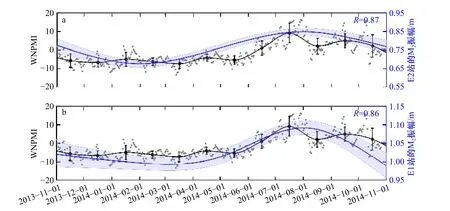
圖13 北太平洋季風指數（WNPMI）與E1 站和E2 站M2 分潮振幅的相關性Fig. 13 The correlation between WNPMI and M2 constituent amplitude of E1 and E2 stations

根據前人研究結果，我們大膽猜測，東亞季風可能通過以下3 個途徑來影響渤海灣M2分潮振幅的季節變化：

（1）影響平均海平面的季節變化。亞洲季風導致了徑流的季節性變化[31]，使得超過60%的黃河水在夏季入海[32]，也使得海河夏季的入海量是冬季的兩倍左右[33]；與此同時，夏季東亞季風導致的渤海上空的東南風使一部分黃河水向北輸送到渤海灣[28]，加上直接匯入渤海灣的海河入海量也增大，使得夏季渤海灣的淡水匯入增多[34]。另一方面，受東亞季風影響，夏季通過渤海海峽從渤海進入黃海的通量比冬季更小[27]。綜上，受東亞季風影響，夏季從黃河和海河匯入渤海灣的淡水增加，與此同時，從渤海流出到黃海的海水更少，共同導致夏季渤海灣平均海平面更高。而潮波的傳播受到水位的影響[13]，因此，受東亞季風季節變化影響的渤海灣平均海平面的季節變化導致了M2分潮振幅的季節變化。

（2）影響層化的季節變化。根據Yanagi 等[35]和Jeon 等[26]的研究，對于渤海灣而言，冬季從陸地到海洋的強西北風會導致海水降溫，破壞之前形成的層化并導致垂向均一的層化狀態。春末夏初，隨著海水表層升溫速率的增加以及黃河和海河入海量的增加，海面風應力和底部摩擦力引起的混合不足以消耗輸入的勢能，使得渤海灣層化逐漸加強[36-37]，并在夏季達到最大值[37]。因此，東亞季風能夠導致層化的季節變化，進而引起M2分潮的季節變化[2]。

（3）影響渦動黏性系數。Pohlmann[38]發現北海的垂向渦黏性具有顯著的年周期并與海面風應力的年變化有關；此外，垂直渦動黏性系數依賴于層化。Maas 和Van Haren[39]證實了層化情況下渦動黏性系數降低的可能性。Howarth[40]認為溫躍層的存在可以

在理想實驗中，根據E2 站的水位觀測數據構建了人造“水位數據”，其中，M2分潮具有時變的振幅和遲角，而S2、K1、O1、MK3、M4分潮及LF1 和LF2 的振幅或遲角是常數。實驗結果表明：無論人造“水位數據”是否存在缺測，EHA 分析所得隨時間變化的M2振幅和遲角以及不隨時間變化的S2、K1和O1分潮的振幅和遲角整體比CHA、SHA、OEHA 等方法的分析結果更接近給定值，表明EHA 是一種行之有效的方法。

利用EHA 分析實際水位觀測數據時，分析結果發現，E1 站和E2 站時變M2分潮振幅具有相同的變化趨勢：夏季大、冬季小。此外，M2分潮振幅的相對變化在E2 站約為11%，在E1 站約為5%。E1 站和E2 站隨時間變化的平均海平面與M2分潮振幅隨時間變化的趨勢相同。EHA 分析所得其他潮汐成分（包括S2，K1和O1）的常數形式的振幅值與CHA 所得結果吻合較好。更重要的是，敏感實驗的結果表明，M2分潮振幅和平均海平面的變化趨勢是魯棒的，不受實驗設置的影響。根據前人研究[2-3,11,13,41]猜測，東亞季風的季節變化引起了平均海平面、層化和渦動黏性系數的季節變化，進而誘導了渤海灣M2分潮振幅的季節變化。降低渦動黏性系數，除此之外，Müller 等[2]指出，層化可以使得水體更加穩定，進而導致夏季的渦動黏性系數比混合均勻的夏季小幾個數量級。因此，受東亞季風影響的層結的季節變化會導致渦動黏性系數的季節變化，進而誘發M2分潮的季節變化。

除了東亞季風可能影響渤海灣M2振幅的季節變化之外，水深、近岸與否等原因也有可能會對M2分潮振幅的季節變化造成影響。對比圖9 和圖10 可知，E1 站和E2 站的MSL 和M2分潮振幅的年變化并不完全一致，這種現象一方面是由數據缺測造成的，另一方面也可能與E1 和E2 兩站的水深、近岸與否的差異有關。Müller 等[2]認為，相比遠離海岸的地區，近岸地區的M2分潮的季節變化更顯著。而在渤海地區，不同的水深和底摩擦系數也會對M2分潮的振幅帶來影響[42]。

5 結論

本文利用EHA 分析了渤海灣E1 站和E2 站一年時間段的水位觀測數據，同時估計了時變的和不隨時間變化的分潮振幅和遲角，來探究渤海灣M2分潮振幅的季節變化。