風生近慣性能通量和地形粗糙度對海洋內部混合的影響*

陳 娟 喬夢甜 曹安州 宋金寶

風生近慣性能通量和地形粗糙度對海洋內部混合的影響*

陳 娟 喬夢甜 曹安州 宋金寶①

（浙江大學海洋學院 舟山 316021）

使用細尺度參數化方法和2015—2019年全球的Argo溫鹽剖面資料, 分析了風生近慣性能通量和地形粗糙度對全球海洋300—600 m深度的渦流擴散系數的影響。結果表明, 在30°—45°N區域, 月均渦流擴散系數與月平均風生近慣性能通量隨時間的變化趨勢較為一致, 相關系數可達0.43, 前者滯后1個月, 與后者的相關系數可達0.65, 但在其他區域二者的變化趨勢相差較大; 相較于中緯度和北半球, 低緯度和南半球的地形粗糙度與擴散系數的相關關系更好。基于這些分析結果, 擬合并建立了30°—45°N區域300—600 m深度的渦流擴散系數與風生近慣性能通量和地形粗糙度的關系式。而且, 用此關系式和細尺度參數化方法計算出來的擴散系數平均量級差異為0.47, 且91%的值偏差小于一個量級。據此, 我們給出了1—12月30°—45°N太平洋區域的渦流擴散系數的網格化結果。

海洋混合; 參數化; 風生近慣性能通量; 地形粗糙度

跨等密度面湍流混合對海洋中的水體交換、背景層結的維持以及區域和全球的翻轉流都有重要影響, 研究湍流混合及其參數化意義重大。在遠離混合層和底邊界層的海洋內部混合, 其主要機制是通過與波-波相互作用相關的小尺度能量級聯引起內波破碎。研究表明, 內波場的能量來源主要是潮汐和風(Munk, 1998; Wunsch, 2004)。風驅動的混合提供了約1 TW(1 TW=1012W)的能量(Munk, 1998; Wunsch, 1998), 風產生的近慣性內波提供了0.3—1.5 TW的能量(Alford, 2001, 2003; Watanabe, 2002; Rimac, 2013), 二者對全球能量平衡均有著重要影響。海洋內部湍流混合主要與渦動能和渦度、潮汐的強度、海底地形的粗糙度以及風對近慣性運動的作用等因素有關(Kunze, 2006; Whalen, 2012; Jing, 2013)。

Munk(1966)基于一維垂向對流擴散方程指出, 為了維持深海的層結, 全球海洋的平均湍流渦流擴散系數至少要達到10–4m2/s。近幾十年來的研究表明, 在遠離邊界的海洋內部擴散率相對較小, 僅10–5m2/s(Polzin, 1997; Kunze, 2006), 但在海山(Kunze, 1997)、峽谷(Carter, 2002)等粗糙地形附近, 湍流混合明顯增強。Wu等(2011)研究南大洋湍流混合的時空變化特征發現渦流擴散系數與地形粗糙度顯著相關, 相關系數可達0.51。研究表明, 海洋渦旋也對湍流混合產生了一定影響, Jing等(2013)發現在300—600 m水深上, 反氣旋渦影響下的混合明顯增強; Yang等(2017)研究南海北部的3個反氣旋渦發現渦旋邊緣的渦流擴散系數明顯高于渦旋中心; 陳娟等(2020)基于Argo剖面數據研究北太平洋渦旋對混合的影響發現, 反氣旋渦增強了300—900 m水深的混合, 氣旋渦影響下, 600—900 m水深的混合增強了18%。風對近慣性運動的作用是上層海洋內波場的主要能量來源之一(Wunsch, 2004)。研究表明, 大多數風生近慣性能通量被輸送到海洋內部, 并在1 000 m深度內耗散(Watanabe, 2008)。Wu等(2011)利用Argo浮標測量的高分辨率水文剖面, 發現南大洋平滑地形上1 500 m深度的跨等密度面混合的季節變化在很大程度上歸因于風生近慣性能通量的季節變化特征。該結果與Jing等(2010)在西北太平洋137°E斷面的研究結果相似。Whalen等(2018)利用Argo浮標資料計算30°—45°N的渦流擴散系數, 發現該區域湍流混合的季節性周期變化和對風生近慣性能通量的響應都至少達到2 000 m深度。然而, 在夏威夷海脊附近的ALOHA站, 發現風生近慣性運動強迫的湍流混合被限制在上層600 m內(Jing, 2011, 2013)。雖然上層海洋的湍流混合受到海表面風應力, 特別是風生近慣性能通量的影響, 但風生近慣性能通量可以向下傳播多深仍不清楚。

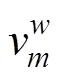
1 數據與方法

1.1 數據資料介紹

本文使用的溫鹽數據是經過中國Argo實時資料中心(http://www.argo.org.cn/)質量再控制的《全球海洋Argo散點資料集》。選取2015—2019年全球范圍內的數據, 并篩選平均垂直分辨率不大于10 m, 測量水深不小于600 m的Argo溫鹽剖面數據。2019年12月全球可用的Argo溫鹽剖面數據共7 049組, 位置分布如圖1所示。

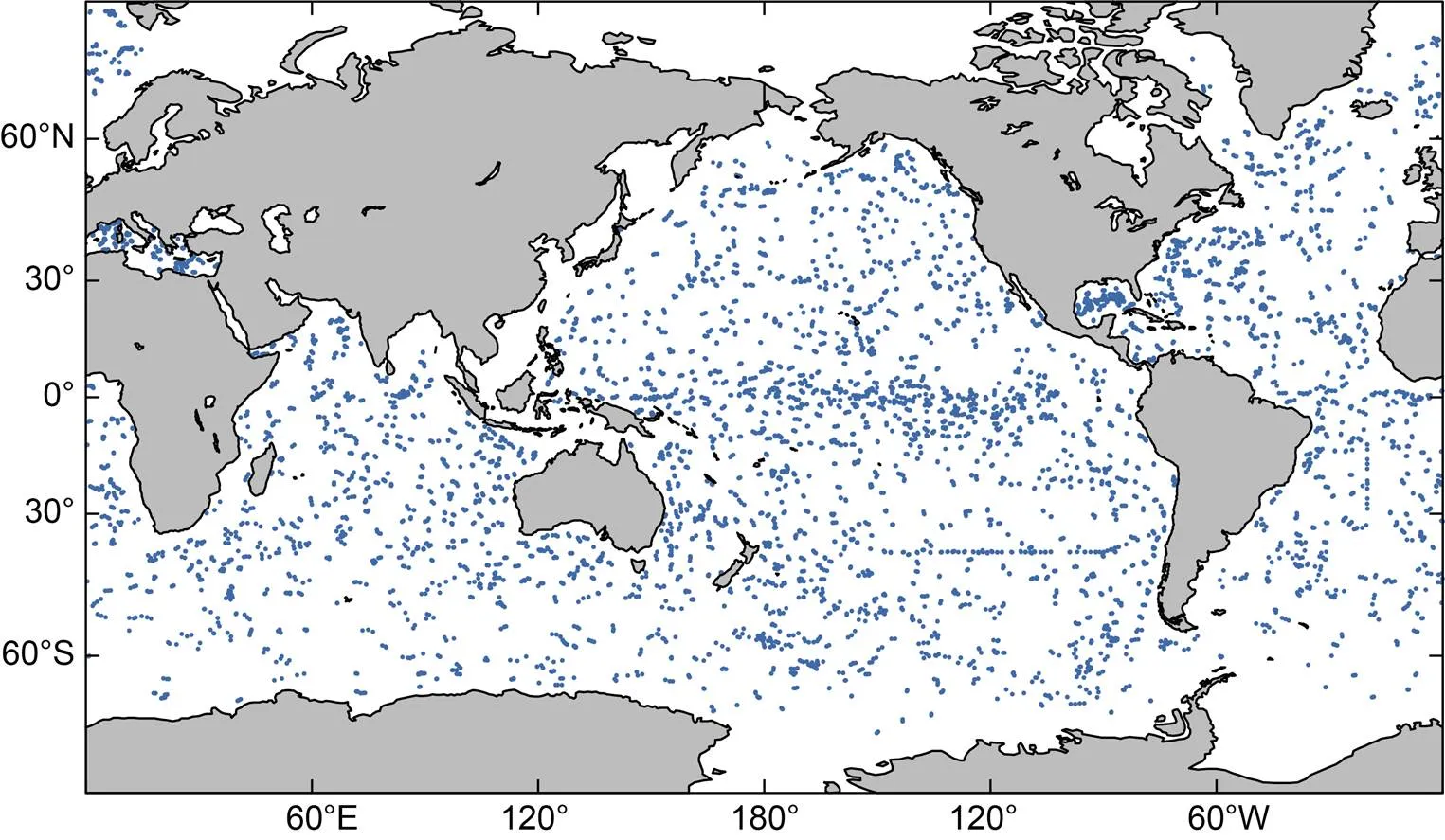
圖1 2019年12月全球Argo剖面分布

注: 圖中藍色點為Argo站位

文中選用的風場資料為美國國家環境預報中心(National Centers for Environmental Prediction, NCEP)發布的高分辨率氣候預報系統再分析(climate forecast system reanalysis, CFSR)風場資料(https://rda.ucar. edu/)。選用2015—2019年的全球風場數據, 時間分辨率為6 h, 空間分辨率約為0.2°×0.2°。

本文選用的地形數據是來自美國海洋大氣管理局(National Oceanic and Atmospheric Administration, NOAA)的ETOPO1基巖模型網格數據(https://www. ngdc.noaa.gov/mgg/global/global.html)。現有的ETOPO1模型是美國地球物理數據中心(National Geophysical Data Center, NGDC)在2008年8月開發的。ETOPO1中使用的測深、地形和海岸線數據來自NGDC, 美國國家航空航天局(National Aeronautics and Space Administration, NASA)等機構。ETOPO1的分辨率是1′×1′, 是現在海洋地球科學研究中使用最為頻繁的數據之一(Amante, 2009)。本文定義的地形粗糙度為1/3°×1/3°網格區域內地形高度的方差(Kunze, 2006; Jing, 2011)。

1.2 基于應變的細尺度參數化方法

假設考慮的波數帶中的剪切或應變變化主要是由內波過程導致的, 內波破碎是由非線性波-波相互作用控制的小尺度能量級聯引起的(Kunze, 2006)。基于以上假設, 渦流擴散系數可以根據細尺度參數化方法進行計算(Polzin, 1997; Kunze, 2006; Wu, 2011), 它將厘米尺度的湍流混合過程與更容易測量到的海洋內波的強度建立起聯系。

Gregg(1989)最早結合海洋流速觀測數據, 根據波-波相互作用和大洋內波譜(Garrett-Munk, GM, Garrett, 1979), 提出了基于流速剪切的細尺度參數化方案:

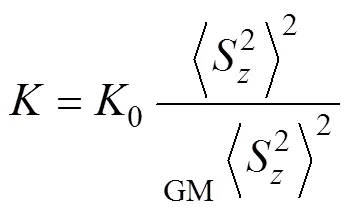
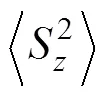
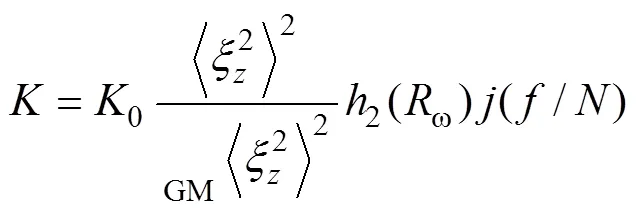
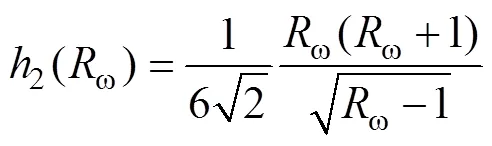
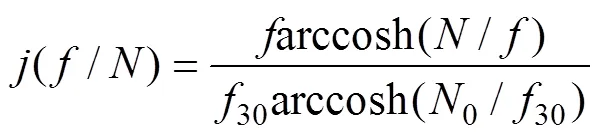
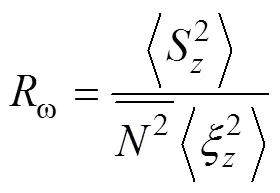
由于缺少流速剖面數據, 且溫鹽剖面數據較為豐富, 本文采用基于應變的細尺度參數化方案計算海洋內部渦流擴散系數。本文選取ω=7(Jing,2011; Zhu,2018)。具體計算和處理過程如下:

本文從300 m深度處開始計算渦流擴散系數, 由于Argo浮標的測量深度大部分小于2 000 m, 為了盡可能多的計算垂向渦流擴散系數, 本文選取測量深度不小于600 m, 垂向精度不大于10 m的溫鹽剖面數據進行計算, 最多計算至1 800 m。將300—1 800 m深度上的溫鹽剖面分割為300 m長度的子剖面, 每段子剖面上的垂向應變的計算公式為:

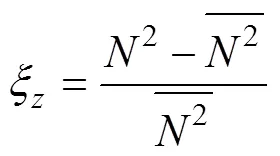
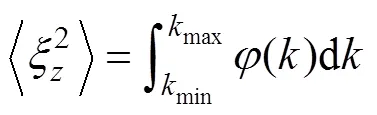
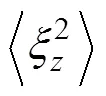
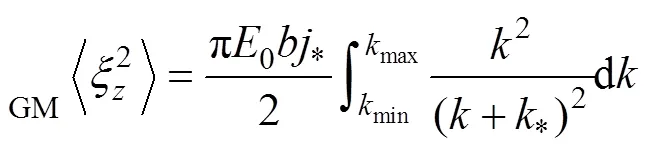
其中,0= 6.3×10-5, 溫躍層垂直尺度=1 300 m, 參考模數*=3, 參考波數*=π*/0(Gregg, 1991)。

本文采用的細尺度參數化方法適用于開闊大洋(Kunze, 2006; Liang, 2018), 本文選取的區域雖然包含部分近岸區域, 但由于經過數據篩選后, 近岸區域符合條件的Argo剖面數據很少, 可以認為細尺度參數化方法基本適用于本文的研究區域。

1.3 風生近慣性能通量的計算

本文利用平板模型(Pollard, 1970; Pollard, 1980; D’Asaro, 1985; Alford, 2001, 2003; Guan, 2014; Cao, 2018)計算風生近慣性流速。該模型假設風應力均勻作用于整個海洋上混合層, 上混合層的運動滿足:

其中,和分別是海洋上混合層內東西和南北方向上的近慣性流速分量,是時間,是科氏參數,τ和τ分別是東西和南北方向上的風應力,是海水密度,m是混合層厚度,是衰減系數。風應力的計算公式為

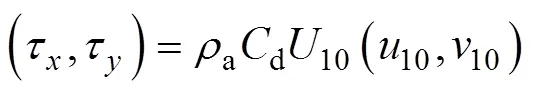
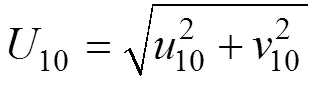
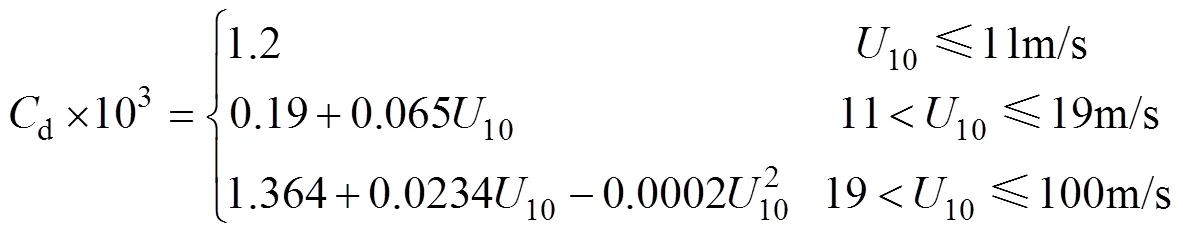
本文采用Alford(2003)提出的譜方法對平板模型進行求解, 得到混合層內東西和南北方向上的近慣性流速分量和。在譜方法中, 衰減系數是隨頻率變化的函數:

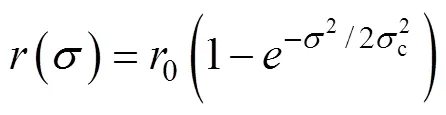
其中,0為常數,c是臨界頻率, 低于此臨界頻率的響應均是Ekman流的影響。隨緯度變化, 所以取為科氏參數的倍數符合近慣性運動衰減規律(Alford, 2001, 2003)。因此本文取0=0.15,c=/2。

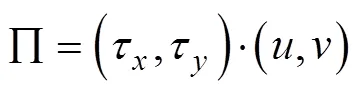
其中,τ和τ分別是東西和南北方向上的風應力,和分別是海洋上混合層內東西和南北方向上的近慣性流速分量。

2 結果與分析

2.1 風生近慣性能通量對海洋內部混合的影響

圖2展示了2015—2019年15°—30°N (S)、30°—45°N (S)、45°—60°N (S) 6個緯度帶范圍內的月平均風生近慣性能通量(wind-induced near-inertial energy flux, WNEF)與海洋內部渦流擴散系數的關系。我們發現, 除了15°—30°N和15°—30°S, 其他4個緯度帶范圍內, 300—600 m深度的月平均渦流擴散系數基本與WNEF的變化趨勢較為一致, 特別是30°—45°N范圍內, 300—600 m深度的渦流擴散系數和WNEF隨時間的變化趨勢高度一致, 與Whalen等(2018)的研究結果一致。如圖3c所示, 在30°—45°N, 即使在600—900 m深度的渦流擴散系數和WNEF仍具有比較一致的時間變化趨勢, 但該現象在其他緯度帶未曾出現。另外, 從圖2c可以明顯看出, 300—600 m深度的渦流擴散系數的峰值滯后于風生近慣性能通量的峰值, 因此, 本文計算了300—600 m深度上月平均垂向渦流擴散系數與WNEF的遲滯相關系數, 計算結果如圖4所示, 圖中橫坐標“1”表示渦流擴散系數相對于WNEF滯后一個月, 以此類推。結果顯示, 滯后的渦流擴散系數與WNEF基本呈現正相關, 且在95%置信區間內顯著。300—600 m深度上, 月平均擴散系數與WNEF的相關系數約為0.43, 相關系數的最大值出現在滯后1個月處, 相關系數約為0.65, 在95%置信區間內顯著。總體來說, 30°—45°N區域300—600 m深度上的渦流擴散系數的時間變化與風生近慣性能通量的時間變化吻合得更好。

2.2 地形粗糙度對海洋內部混合的影響

為了分析地形粗糙度(topographic roughness)T對海洋內部渦流擴散系數的影響, 本文計算了15°—30°N (S)、30°—45°N (S)、45°—60°N (S)緯度帶范圍內的平均垂向渦流擴散系數(log10)與地形粗糙度(log10T)的擬合關系及相關系數, 結果如圖5所示。在15°—30°N (S)區域, 渦流擴散系數的擬合結果基本在計算結果的中間, 擴散率明顯隨地形粗糙度的增加而增大, 相關系數約為0.4; 在渦流擴散系數的季節特征更為明顯的30°—45°N區域, 擬合結果的斜率更小且相關系數僅約為0.15, 30°—45°S的擬合結果斜率和相關系數均略大于30°—45°N的結果; 在更高緯度, 擬合結果的斜率和相關系數均更小。總體來說, 南半球的垂向平均渦流擴散系數與地形粗糙度的正相關關系比北半球更加明顯, 且在低緯度, 擴散率隨地形粗糙度的增加而增大的趨勢更明顯, 并且低緯度和南半球的擴散率計算結果在擬合結果的兩側分布更為集中。

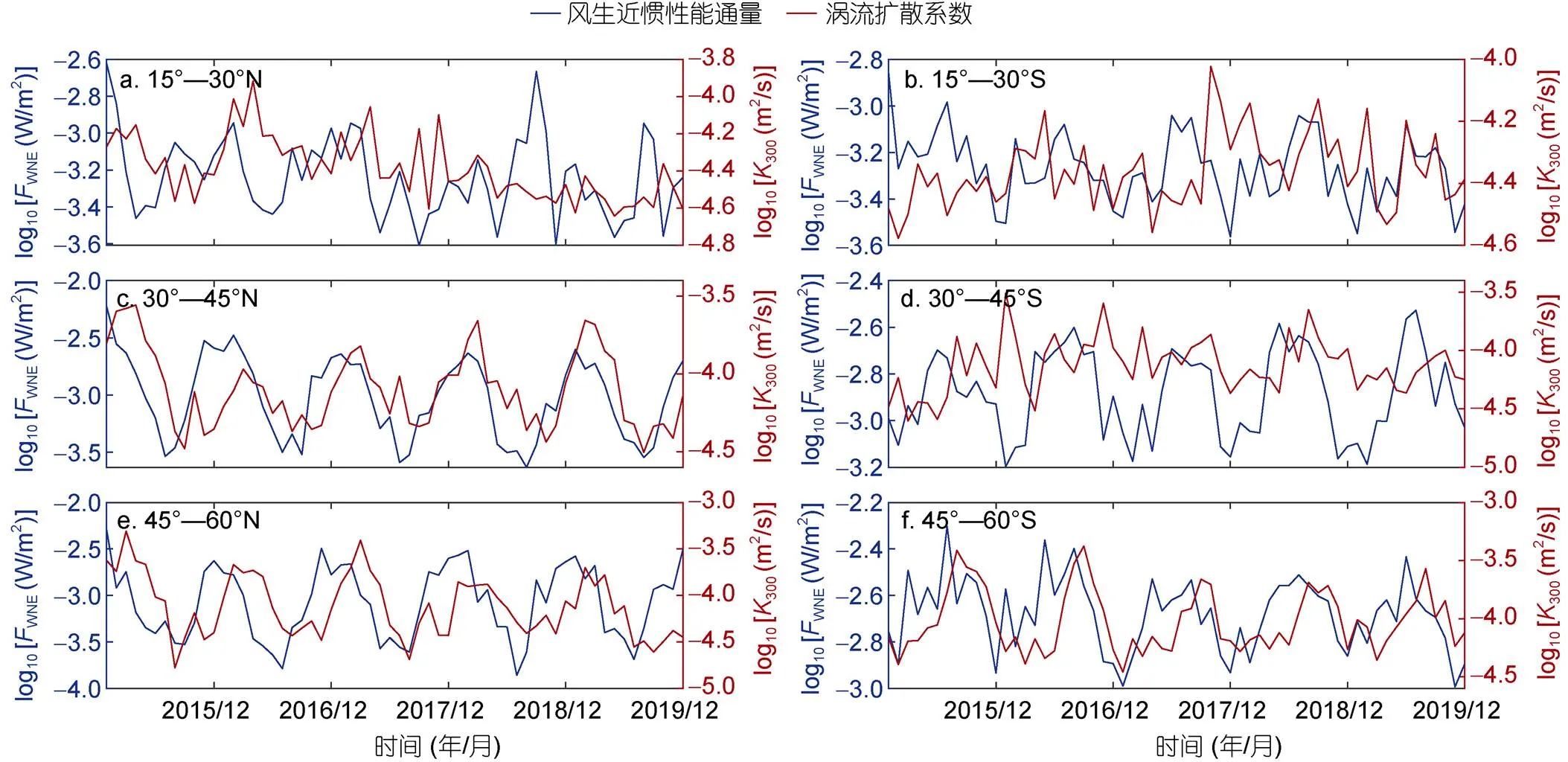
圖2 在15°—30°N(S)、30°—45°N(S)和45°—60°N(S)緯度帶范圍內的月平均風生近慣性能通量與月均300—600 m深度的渦流擴散系數的關系

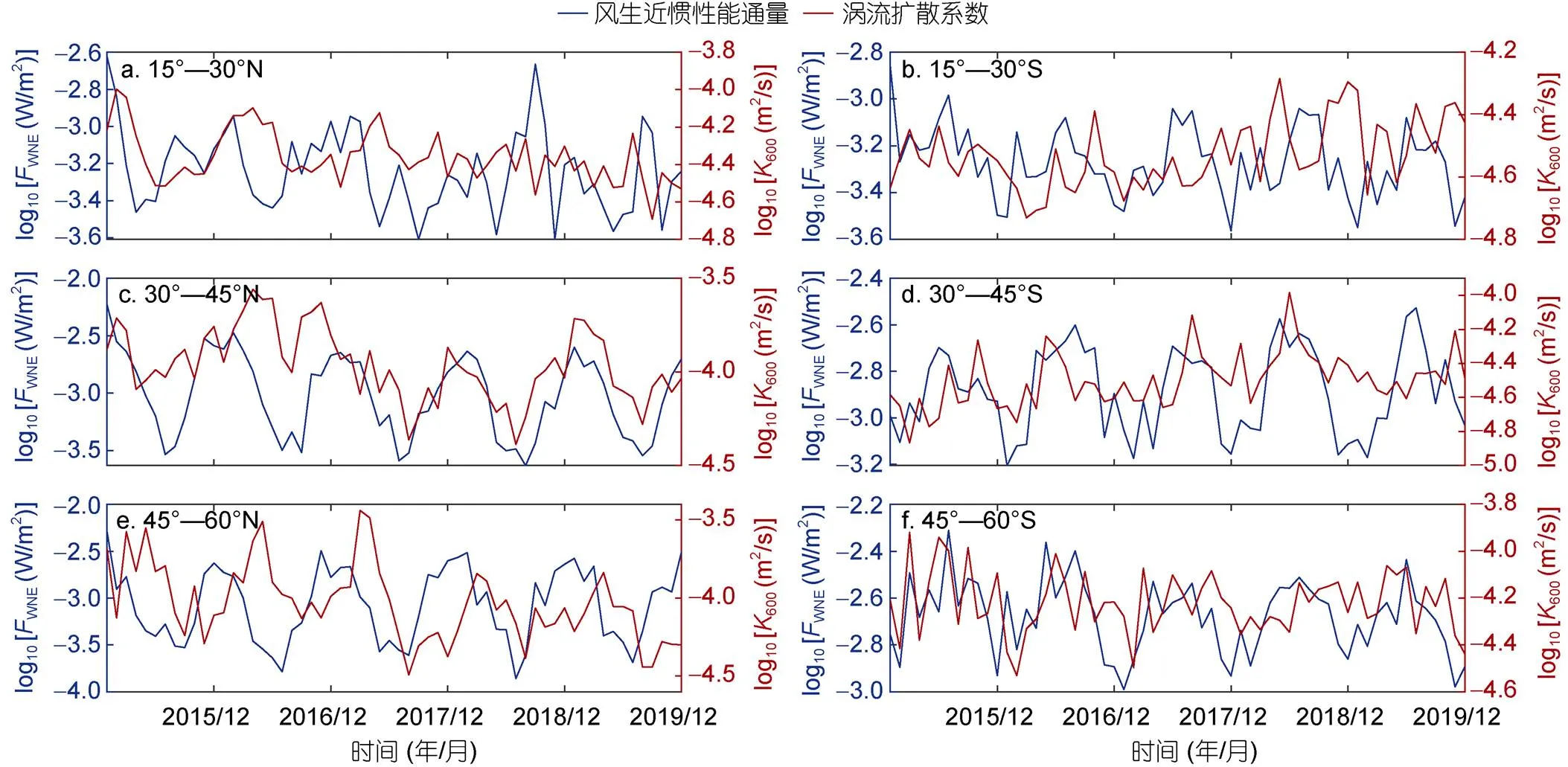
圖3 在15°—30°N(S)、30°—45°N(S)和45°—60°N(S)緯度帶范圍內的月平均風生近慣性能通量與月均600—900 m深度的渦流擴散系數的關系

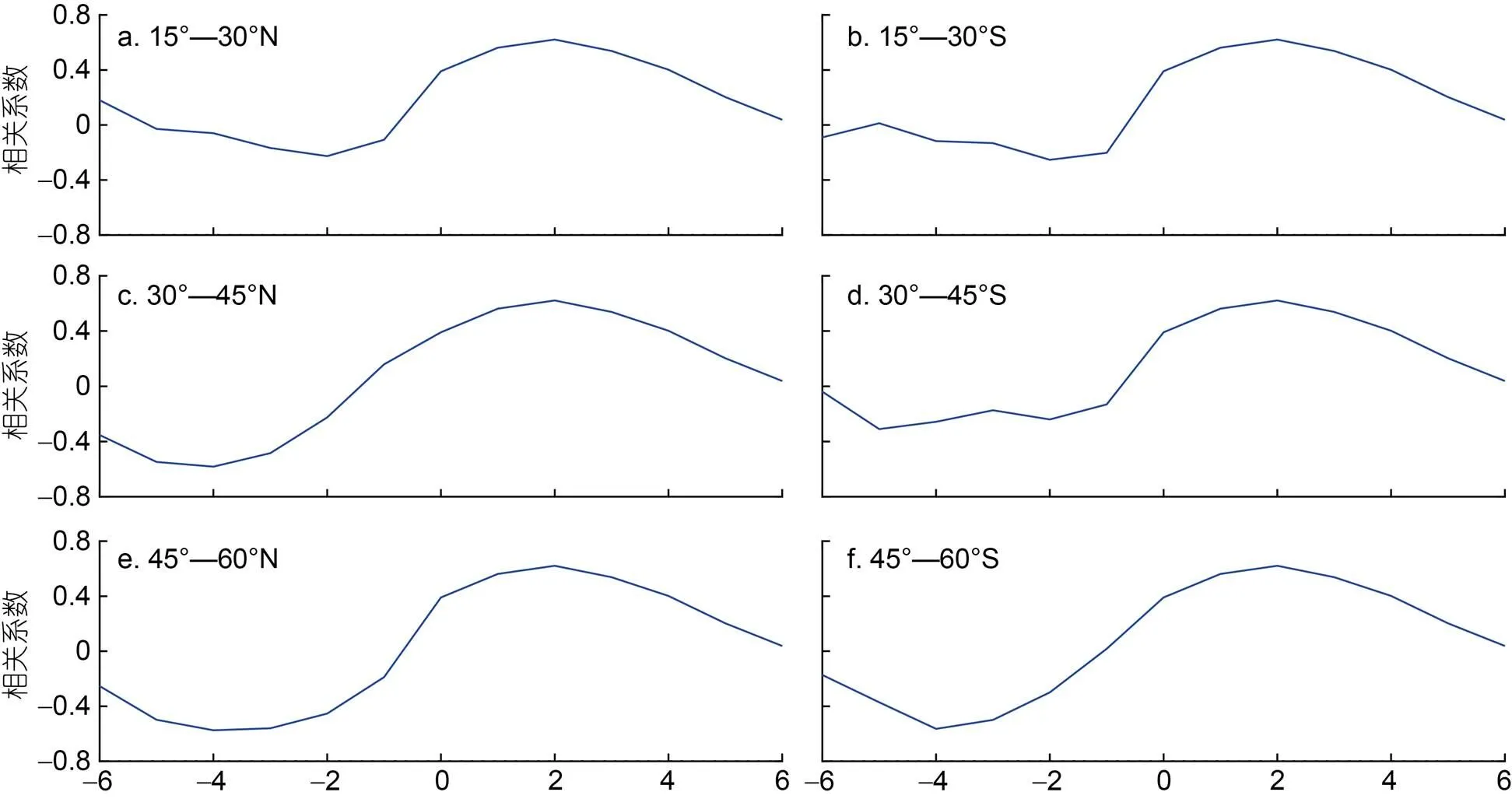
圖4 在15°—30°N(S)、30°—45°N(S)和45°—60°N(S)緯度帶范圍內300—600 m深度上月平均垂向渦流擴散系數與風輸入近慣性能通量的遲滯相關系數

因為前面的研究表明, 海洋內部的渦流擴散系數與風生近慣性能通量在300—600 m深度上的相關關系更好, 為了與之對應, 如圖6所示, 我們計算了300—600 m深度的渦流擴散系數(log10300)與地形粗糙度(log10T)的擬合關系及相關系數。與圖5的結果相似, 該片段的渦流擴散系數在低緯度和南半球與地形粗糙度的相關關系更好, 且擴散率分布更為集中, 但6個緯度帶的擬合結果斜率和相關系數均低于圖5中的結果。在30°—45°N區域, 300—600 m深度的渦流擴散系數與地形粗糙度的擬合斜率為0.1, 相關系數約為0.13, 在95%置信區間內顯著。

本文還另外使用ETOPO2地形數據計算了地形粗糙度, 結果顯示, ETOPO2與ETOPO1地形數據的計算結果在數值上存在差異, 但相差不大, 表明在一定分辨率以內, 地形粗糙度的計算結果對分辨率不太敏感, 數據分辨率高低對地形粗糙度與渦流擴散系數的擬合結果影響較小。

2.3 擬合結果

根據上述研究結果, 本文采用最小二乘法對30°—45°N區域的風生近慣性能通量、地形粗糙度以及300—600 m深度的渦流擴散系數進行擬合, 結果如圖7所示。擬合關系式為

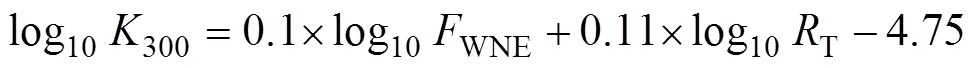
其中,300表示300—600 m深度的渦流擴散系數的值,WNE表示風生近慣性能通量的值,T表示地形粗糙度的值。根據計算得出, 300—600 m深度的渦流擴散系數的計算值在3倍擬合結果和10倍擬合結果(即一個量級)以內的占比分別為60%和91%, 因此, 我們認為此擬合關系式是可以接受的。

為了詳細分析根據細尺度參數化方法計算的渦流擴散系數與根據擬合公式計算的渦流擴散系數之間的差異, 如圖8所示, 本文計算了渦流擴散系數的擬合結果與計算結果的量級差異分布。結果顯示, 隨著量級差異的增大, 分布的數量越來越少, 90%的量級差異小于1個量級, 平均量級差為0.47個量級, 量級差的中位數約為0.38。

為了根據擬合關系式給出1—12月30°—45°N區域的渦流擴散系數網格化結果, 本文將月平均風生近慣性能通量和地形粗糙度數據統一劃分為0.25°×0.25°的網格進行計算, 并展示該緯度范圍內太平洋區域的結果。30°—45°N的太平洋區域的地形粗糙度如圖9所示, 在日本群島以東的日本海溝和中太平洋(30°—45°N, 170°E—170°W)區域地形較為復雜, 粗糙度可達106m2。該區域月平均風生近慣性能通量如圖10所示, 該區域WNEF的值主要分布在-4—-2量級內, 且該區域西北太平洋整體的WNEF高于東北太平洋, 冬季(12—2月)明顯高于其他季節, 夏季(6—8月)的WNEF最低, 符合風場的季節變化規律。

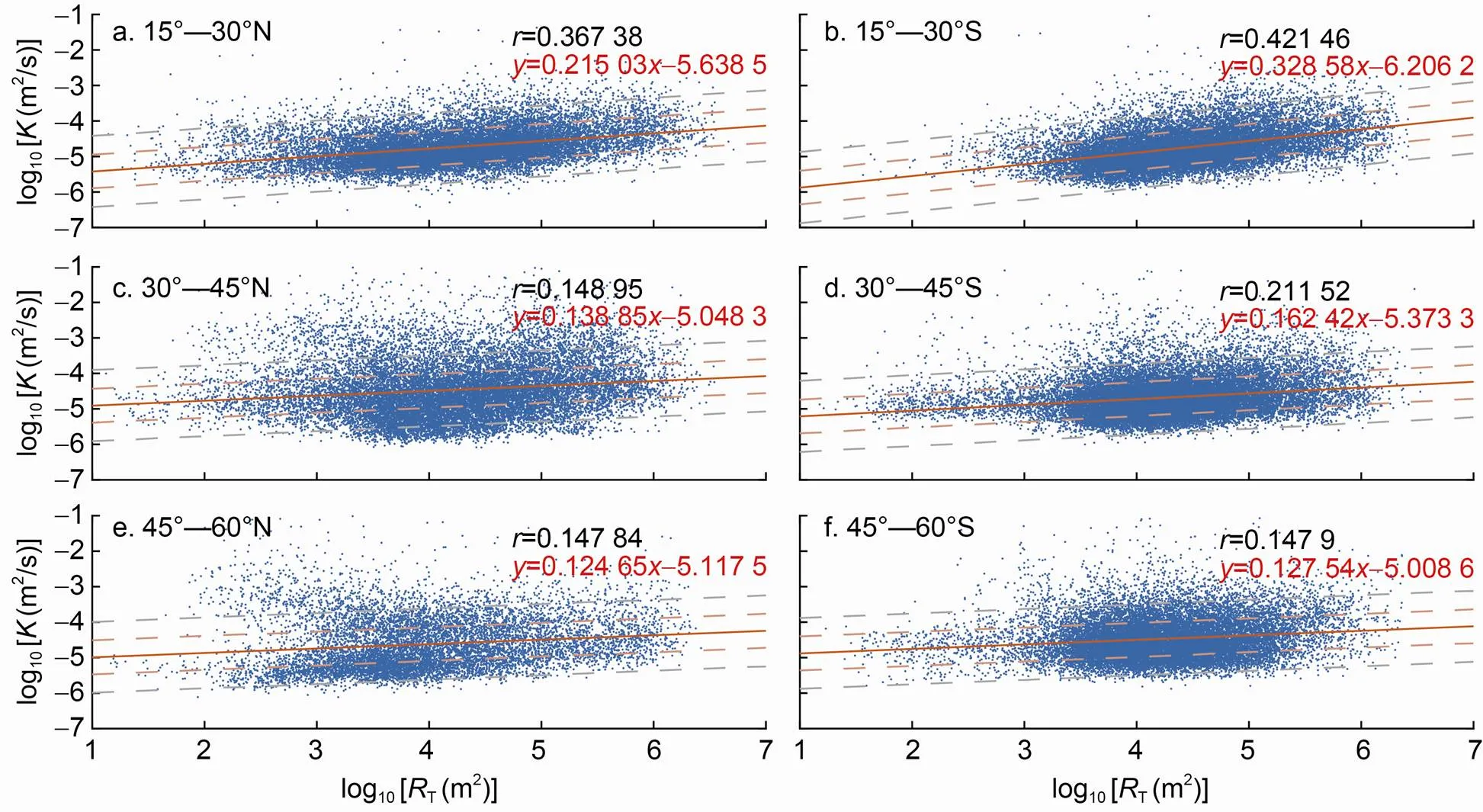
圖5 在15°—30°N(S)、30°—45°N(S)和45°—60°N(S)緯度帶范圍內的垂向平均渦流擴散系數(log10K)與地形粗糙度(log10RT)的擬合關系及相關系數

注: 紅色實線表示擬合結果, 紅色和灰色虛線分別表示3倍擬合結果和10倍擬合結果(即一個量級), 藍色散點表示垂向平均渦流擴散系數的計算結果

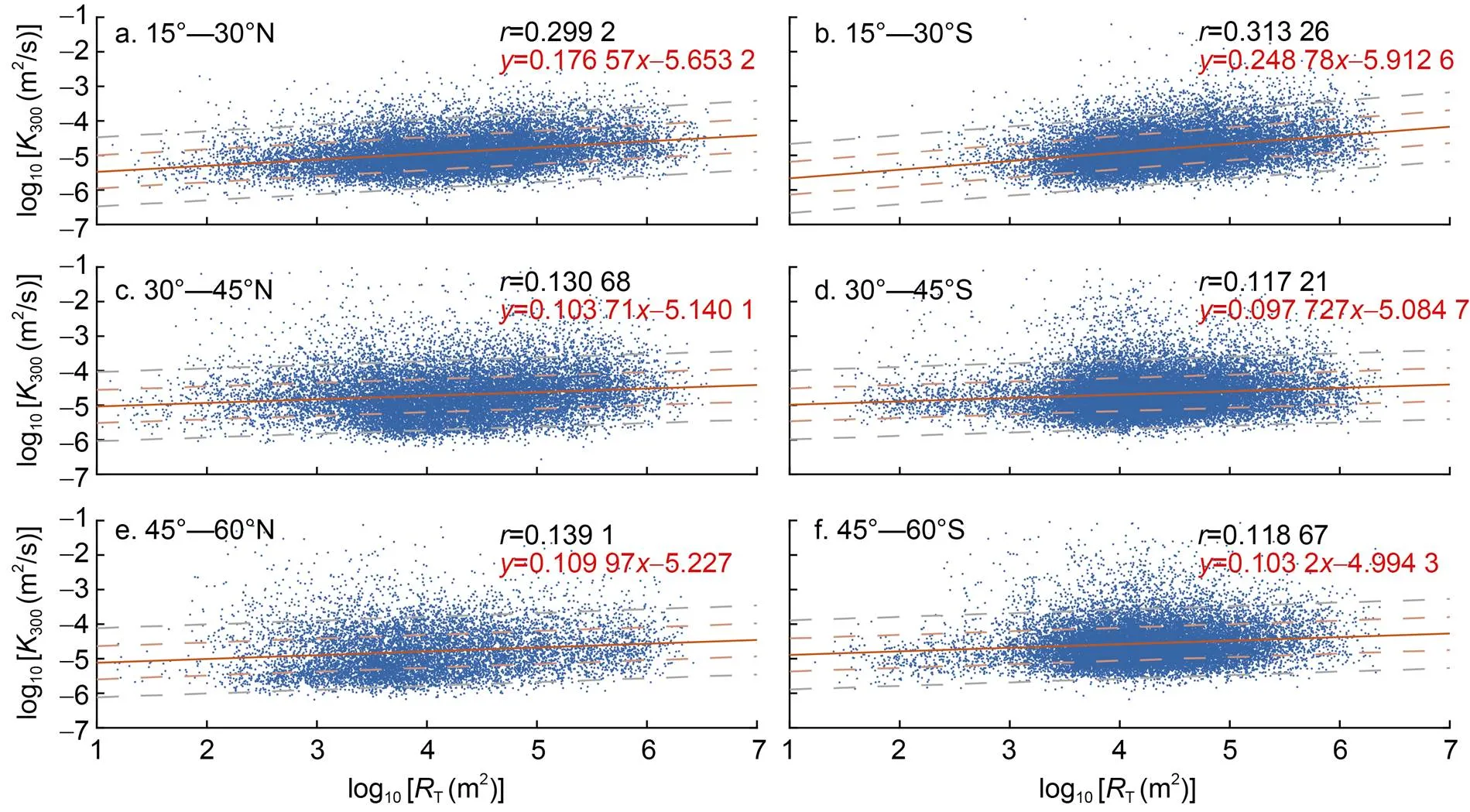
圖6 在15°—30°N(S)、30°—45°N(S)和45°—60°N(S)緯度帶范圍內300—600m深度的渦流擴散系數(log10K300 )與地形粗糙度(log10RT)的擬合關系及相關系數

注: 紅色實線表示擬合結果, 紅色和灰色虛線分別表示3倍擬合結果和10倍擬合結果(即一個量級), 藍色散點表示300—600 m深度的渦流擴散系數的計算結果

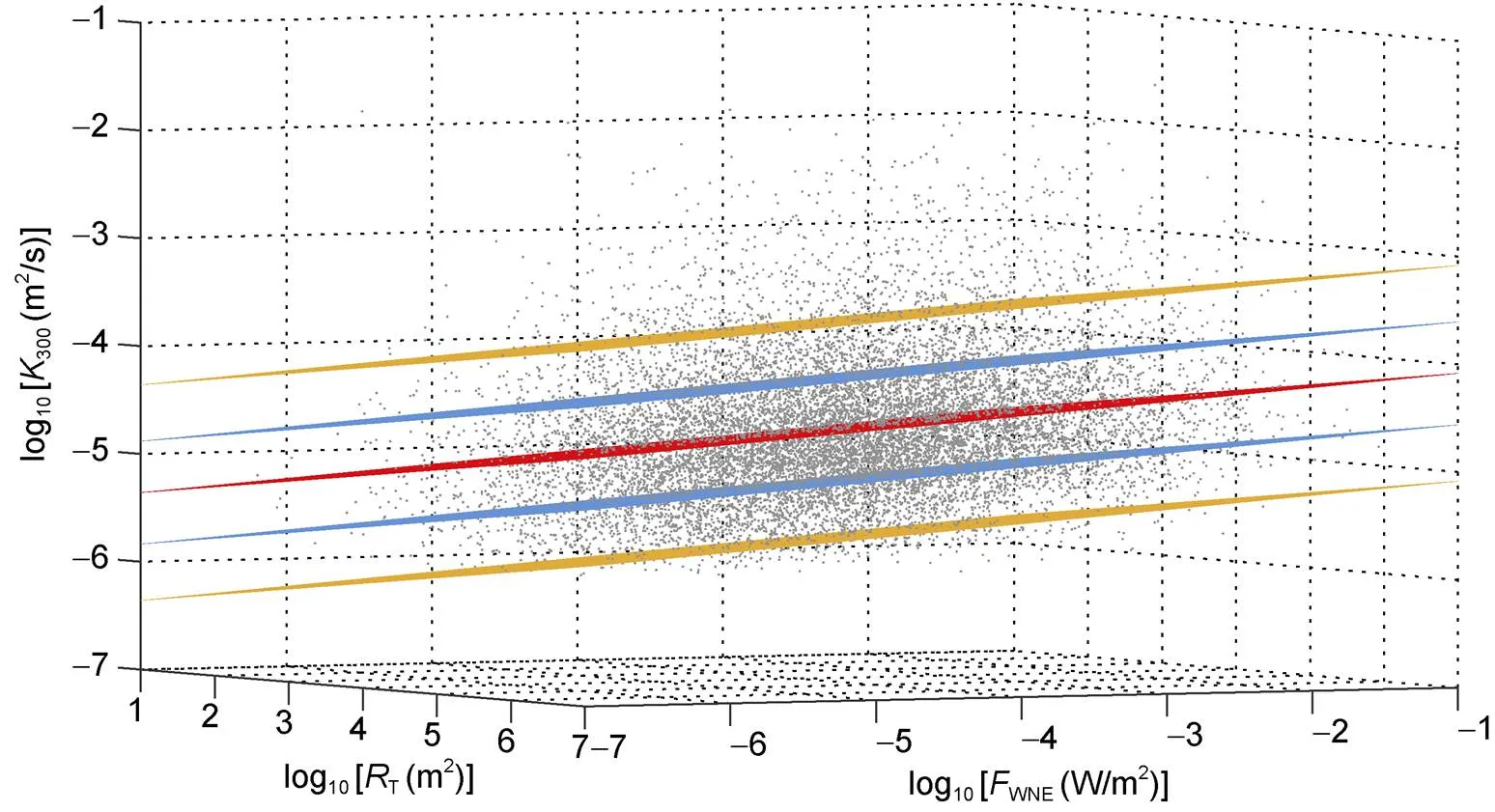
圖7 300—600 m深度的渦流擴散系數與風生近慣性能通量、地形粗糙度的擬合結果

注: 中間紅色平面表示擬合結果平面, 兩側藍色和黃色平面分別表示3倍擬合結果和10倍擬合結果(即一個量級)的平面, 灰色散點表示渦流擴散系數的計算結果

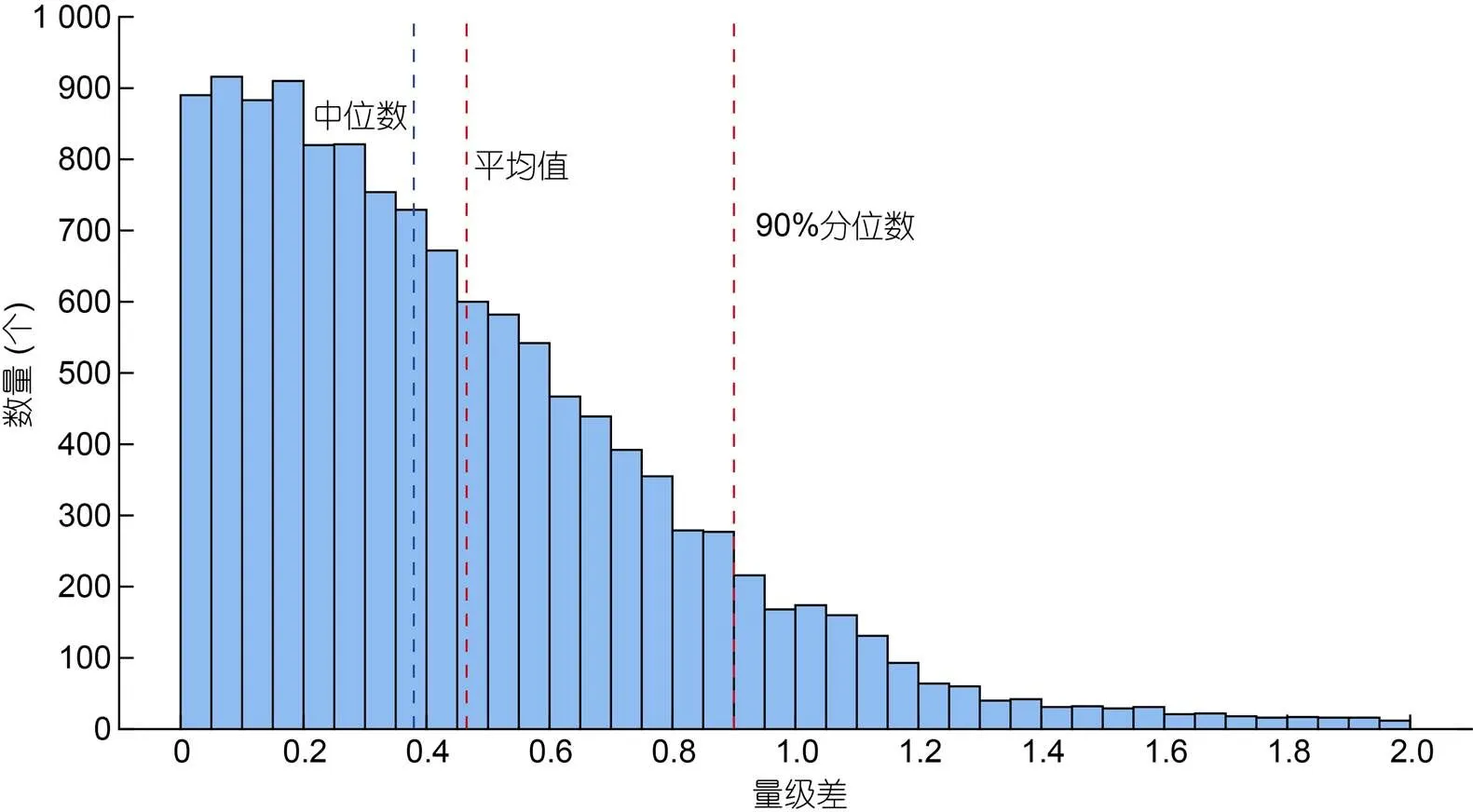
圖8 渦流擴散系數的擬合結果與計算結果的量級差異分布直方圖

利用公式(13), 本文根據風生近慣性能通量和地形粗糙度數據計算的1—12月30°—45°N太平洋區域300—600 m深度上渦流擴散系數的擬合結果如圖11所示。圖中顯示, 渦流擴散系數的擬合結果主要在-5—-4量級內, 并且此區域的西北太平洋的渦流擴散系數明顯高于東北太平洋, 11—4月的渦流擴散系數明顯高于其他月份, 與風生近慣性能通量(圖10)的變化較為一致; 在日本海溝和中太平洋地形粗糙的區域, 渦流擴散系數明顯增大。以此擬合結果(圖11)代替KPP方案中內波破碎導致的渦流擴散系數(僅適用于30°—45°N), 使KPP方案中這一部分的擴散率從常數變為隨時間、區域而變化, 進而改進海洋模式的模擬結果。

圖9 30°—45°N太平洋地形粗糙度

注: 地形粗糙度的取值是log10取對數后的結果

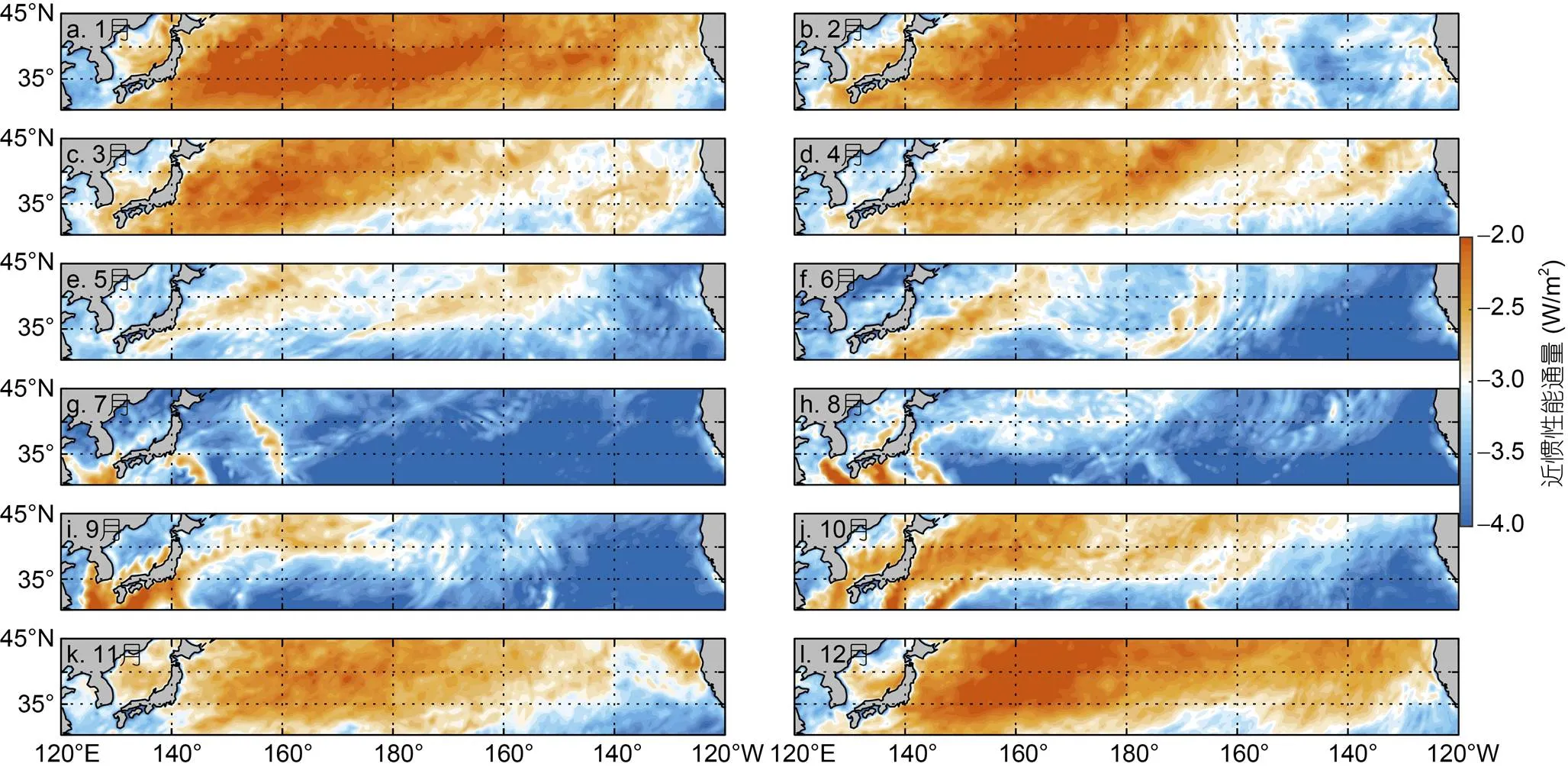
圖10 30°—45°N太平洋1—12月月均風生近慣性能通量

注: 風生近慣性能通量的取值是log10取對數后的結果

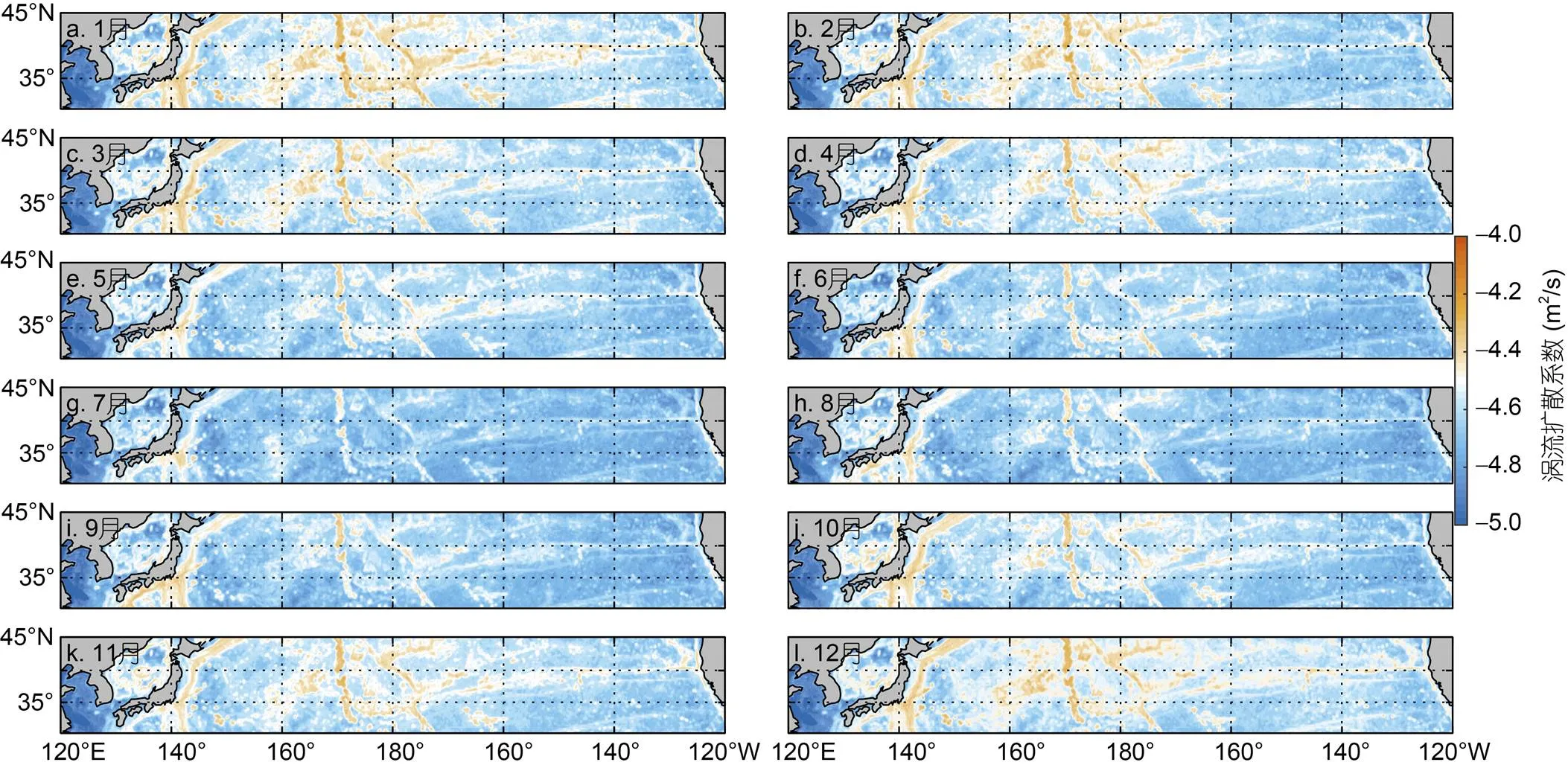
圖11 1—12月太平洋30°—45°N區域300—600 m深度的渦流擴散系數的擬合結果

注: 渦流擴散系數的取值是log10取對數后的結果

3 結論

通過研究全球2015—2019年15°—30°N(S)、30°—45°N(S)、45°—60°N(S) 6個緯度帶范圍內的風生近慣性能通量和地形粗糙度對海洋內部渦流擴散系數的影響, 我們發現:

(1) 在30°—45°N區域, 300—600 m深度的渦流擴散系數和月平均風生近慣性能通量隨時間(月份)的變化趨勢高度一致, 相關系數約為0.43; 滯后一個月的300—600 m深度的渦流擴散系數與月平均風生近慣性能通量的相關性更好, 相關系數可達0.65;

(2) 相對于中緯度和北半球, 低緯度和南半球的垂向平均擴散率與地形粗糙度的相關關系更好; 在30°—45°N區域, 300—600 m深度的渦流擴散系數隨地形粗糙度的增加而增大, 但相關性一般, 相關系數僅為0.13;

(3) 30°—45°N, 300—600 m深度的渦流擴散系數與風生近慣性能通量、地形粗糙度之間的擬合關系式為log10300=0.1×log10WNE+0.11×log10T-4.75; 該區域300—600 m深度的渦流擴散系數的計算值在3倍擬合結果和10倍擬合結果(即一個量級)以內的占比分別為60%和91%; 該深度范圍的渦流擴散系數的擬合結果與計算結果的平均量級差異為0.47個量級; 1—12月渦流擴散系數的擬合結果的空間分布明顯受到風生近慣性能通量和地形粗糙度的影響, 空間和時間變化基本符合地形分布特征和風場變化特征。

Kunze(1985)指出在地轉流背景下, 地轉渦度將內波波段下限從科氏頻率移動至有效科氏頻率eff(eff=+), 反氣旋渦附近的近慣性波的固有頻率可能小于周圍海域的有效科氏頻率, 加劇了近慣性能量向下傳播。因此海洋中尺度渦旋對近慣性內波能量傳遞產生重要影響, 可能進而影響了海洋內部混合。本文僅考慮了風生近慣性能通量和地形粗糙度對海洋內部混合的影響, 未考慮反氣旋渦對風生近慣性能量的影響, 可能對擬合結果存在一定的影響。本文在30°—45°N區域渦流擴散系數的擬合結果呈現出明顯的西強東弱, 特別是黑潮延伸體區域, 除了風生近慣性能通量對海洋內部混合的直接影響, 可能也間接受到了中尺度渦旋的影響。

陳 娟, 李少峰, 曹安州等, 2020. 北太平洋渦旋對基于細尺度參數化的海洋內部混合的影響. 海洋與湖沼, 51(2): 248—257

Alford M H, 2001. Internal swell generation: the spatial distribution of energy flux from the wind to mixed layer near-inertial motions. Journal of Physical Oceanography, 31(8): 2359—2368

Alford M H, 2003. Improved global maps and 54-year history of wind-work on ocean inertial motions. Geophysical Research Letters, 30(8): 122—137, 1424, doi:10.1029/2002GL016614

Amante C, Eakins B W, 2009. ETOPO1 1 Arc-Minute Global Relief Model: procedures, data sources and analysis. NOAA Technical Memorandum NESDIS NGDC-24, 1(1): 1—25, doi: 10.7289/V5C8276M

Cao A Z, Guo Z, Song B, 2018. Near-inertial waves and their underlying mechanisms based on the South China Sea Internal Wave Experiment (2010-2011). Journal of Geophysical Research: Oceans, 123(7): 5026—5040

Carter G S, Gregg M C, 2002. Intense, variable mixing near the head of Monterey submarine canyon. Journal of Physical Oceanography, 32(11): 3145—3165

D’Asaro E A, 1985. The energy flux from the wind to near-inertial motions in the surface mixed layer. Journal of Physical Oceanography, 15(8): 1043—1059

Garabato A C N, Polzin K L, King B A, 2004. Widespread intense turbulent mixing in the Southern Ocean. Science, 303(5655): 210—213

Garrett C, Munk W, 1979. Internal waves in the ocean. Annual Review of Fluid Mechanics, 11(1): 339—369, https://www. annualreviews.org/doi/abs/10.1146/annurev.fl.11.010179.002011

Gregg M C, 1989. Scaling turbulent dissipation in the thermocline. Journal of Geophysical Research: Oceans, 94(C7): 9686—9698

Gregg M C, Kunze E, 1991. Shear and strain in Santa Monica Basin. Journal of Geophysical Research: Oceans, 96(C9): 16709—16719

Gregg M C, Sanford T B, Winkel D P, 2003. Reduced mixing from the breaking of internal waves in equatorial waters. Nature, 422(6931): 513—515

Guan S D, Zhao W, Huthnance J, 2014. Observed upper ocean response to typhoon Megi (2010) in the Northern South China Sea. Journal of Geophysical Research: Oceans, 119(5): 3134—3157

Henyey F S, 1991. Acoustic scattering from ocean microbubble plumes in the 100 Hz to 2 kHz region. The Journal of the Acoustical Society of America, 90(1): 399—405, doi: 10.1121/1.401264

Jing Z, Wu L X, 2010. Seasonal variation of turbulent diapycnal mixing in the northwestern Pacific stirred by wind stress. Geophysical Research Letters, 37(23): L23604

Jing Z, Wu L X, 2013. Low-frequency modulation of turbulent diapycnal mixing by anticyclonic eddies inferred from the hot time series. Journal of Physical Oceanography, 43(4): 824—835

Jing Z, Wu L X, Li L, 2011. Turbulent diapycnal mixing in the subtropical northwestern Pacific: spatial-seasonal variations and role of eddies. Journal of Geophysical Research: Oceans, 116(C10): C10028, doi: 10.1029/2011jc007142

Kunze E, 1985. Near-inertial wave propagation in geostrophic shear. Journal of Physical Oceanography, 15(5): 544—565

Kunze E, Firing E, Hummon J M, 2006. Global abyssal mixing inferred from lowered ADCP shear and CTD strain profiles. Journal of Physical Oceanography, 36(8): 1553—1576

Kunze E, Toole J M, 1997. Tidally driven vorticity, diurnal shear, and turbulence atop fieberling seamount. Journal of Physical Oceanography, 27(12): 2663—2693

Large W G, McWilliams J C, Doney S C, 1994. Oceanic vertical mixing: a review and a model with a nonlocal boundary layer parameterization. Reviews of Geophysics, 32(4): 363—403

Li Y, Xu Y S, 2014. Penetration depth of diapycnal mixing generated by wind stress and flow over topography in the northwestern Pacific. Journal of Geophysical Research: Oceans, 119(8): 5501—5514

Liang C R, Shang X D, Qi Y F, 2018. Assessment of fine-scale parameterizations at low latitudes of the North Pacific. Scientific Reports, 8(1): 10281

Munk W H, 1966. Abyssal recipes. Deep Sea Research and Oceanographic Abstracts, 13(4): 707—730

Munk W H, 1981. Internal Waves and Small-Scale Processes Evolution of Physical Oceanography. Cambridge: The MIT Press, 264—291

Munk W, Wunsch C, 1998. Abyssal recipes II: Energetics of tidal and wind mixing. Deep Sea Research Part I: Oceanographic Research Papers, 45(12): 1977—2010

Oey L Y, Ezer T, Wang D P, 2006. Loop current warming by hurricane Wilma. Geophysical Research Letters, 33(8): L08613, doi: 10.1029/2006GL025873

Pollard R T, 1980. Properties of near-surface inertial oscillations. Journal of Physical Oceanography, 10(3): 385—398

Pollard R T, Millard Jr R C, 1970. Comparison between observed and simulated wind-generated inertial oscillations. Deep Sea Research and Oceanographic Abstracts, 17(4): 813—816, IN5, 817—821

Polzin K L, Toole J M, Ledwell J R, 1997. Spatial variability of turbulent mixing in the abyssal ocean. Science, 276(5309): 93—96

Polzin K L, Toole J M, Schmitt R W, 1995. Finescale parameterizations of turbulent dissipation. Journal of Physical Oceanography, 25(3): 306—328

Rimac A, von Storch J S, Eden C, 2013. The influence of high-resolution wind stress field on the power input to near-inertial motions in the ocean. Geophysical Research Letters, 40(18): 4882—4886

Watanabe M, Hibiya T, 2002. Global estimates of the wind-induced energy flux to inertial motions in the surface mixed layer. Geophysical Research Letters, 29(8): 64-1—64-3

Watanabe M, Hibiya T, 2008. Energetics of wind-induced turbulent mixing in the ocean. Journal of Oceanography, 64(1): 131—140

Whalen C B, Mackinnon J A, Talley L D, 2018. Large-scale impacts of the mesoscale environment on mixing from wind-driven internal waves. Nature Geoscience, 11(11): 842—847, doi:10.1038/s41561-018-0213-6

Whalen C B, Talley L D, MacKinnon J A, 2012. Spatial and temporal variability of global ocean mixing inferred from Argo profiles. Geophysical Research Letters, 39(18): L18612, doi: 10.1029/2012GL053196

Wijesekera H, Padman L, Dillon T, 1993. The Application of Internal-Wave Dissipation Models to a Region of Strong Mixing. Journal of Physical Oceanography, 23(2): 269—286

Wu L X, Jing Z, Riser S, 2011. Seasonal and spatial variations of Southern Ocean diapycnal mixing from Argo profiling floats. Nature Geoscience, 4(6): 363—366

Wunsch C, 1998. The work done by the wind on the oceanic general circulation. Journal of Physical Oceanography, 28(11): 2332—2340

Wunsch C, Ferrari R, 2004. Vertical mixing, energy, and the general circulation of the oceans. Annual Review of Fluid Mechanics, 36: 281—314

Yang Q X, Zhao W, Liang X F, 2017. Elevated mixing in the periphery of mesoscale eddies in the South China Sea. Journal of Physical Oceanography, 47(4): 895—907

Zhu Y C, Zhang R H, 2018. An Argo-derived background diffusivity parameterization for improved ocean simulations in the tropical pacific. Geophysical Research Letters, 45(3): 1509—1517

INFLUENCE OF WIND-INDUCED NEAR-INERTIAL ENERGY FLUX AND TOPOGRAPHIC ROUGHNESS ON OCEAN INTERNAL MIXING

CHEN Juan, QIAO Meng-Tian, CAO An-Zhou, SONG Jin-Bao

(Ocean College, Zhejiang University, Zhoushan 316021, China)

Using the fine-scale parameterization method and the global Argo data in 2015—2019, the influence of wind-induced near-inertial energy flux and topographic roughness on ocean internal eddy diffusion in 300—600 m depth were analyzed. Results show that, in the Pacific region of 30°—45°N, the trend of the monthly average eddy diffusion coefficient was consistent with the monthly average wind-induced near-inertial energy flux, and the correlation coefficient was ～0.43. The correlation coefficient between the former with a lag of one month and the latter was up to 0.65. However, the trend of the two was quite different in other regions. The correlation between the topographic roughness and eddy diffusion coefficient in the low latitude and southern hemisphere was greater than that of the mid-latitude and northern hemisphere. The analysis shows, in the region of 30°—45°N, the equation describing the relationship between the eddy diffusion coefficient in 300—600 m depth and the wind-induced near-inertial energy flux and topographic roughness was established. The difference between the average magnitude of eddy diffusion coefficientcalculated by this formula and by the fine-scale parameterization method was 0.47, and 91% of the value deviation was within one order of magnitude. At last, the gridded results of eddy diffusion coefficients in the Pacific region of 30°—45°N from January to December were given.

ocean mixing; parameterization; wind-induced near-inertial energy flux; topographic roughness

P731

10.11693/hyhz20210100017

* 國家重點研發計劃項目，2016YFC1401404號，2017YFA0604102號。陳 娟，碩士研究生，E-mail: 21834017@zju.edu.cn

宋金寶，教授，E-mail: songjb@zju.edu.cn

2021-01-18，

2021-03-25