復合歐拉函數方程φ(n-φ(φ(n)))=6,8,10,12,16的正整數解
趙祈芬,雷興輝,張永華
(安康職業技術學院,陜西 安康 725000)
對于正整數n,φ(n)是著名的Euler函數,φ(n)定義為在序列1,2,…,n-1中與n互素的整數的個數[1]。張天平[2]討論了復合歐拉函數方程φ(φ(n))=2Ω(n)的奇數解的問題;田呈亮[3]討論了復合歐拉函數方程φ(φ(n))=2Ω(n)的正整數解的問題;多布杰[4]討論了復合歐拉函數方程φ(φ(n))=2t的可解性問題;王洋、張四保[5]討論了復合歐拉函數方程φ(φ(n-φ(φ(n))))=2的可解性問題;袁合才[6]討論了復合歐拉函數方程φ(φ(n-φ(φ(n))))=4,6的可解性問題;張明麗[7]討論了復合歐拉函數方程φ(φ(n-φ(φ(n))))=8,10的可解性問題。本文研究了復合歐拉函數方程φ(n-φ(φ(n)))=6,8,10,12,16的可解性問題。
1 若干引理

引理2[8]當n≥2時,有φ(n) 定理1 復合歐拉函數方程φ(n-φ(φ(n)))=6 (1)的正整數解:n=9,11,13,17,22。 證明:因為φ(n-φ(φ(n)))=6,所以n-φ(φ(n))=7,9,14,18,下面分4種情況加以討論: 情形一:若n-φ(φ(n))=7,則由引理4,知8≤n≤13,將其逐一代入驗證,經檢驗n=9,11滿足n-φ(φ(n))=7,即n=9,11為(1)式的解。 情形二:若n-φ(φ(n))=9,則由引理4,知10≤n≤17,將其逐一代入驗證,經檢驗n=13,17滿足n-φ(φ(n))=9,即n=13,17為(1)式的解。 情形三:若n-φ(φ(n))=14,則由引理4,知15≤n≤27,將其逐一代入驗證,經檢驗n-φ(φ(n))=14不成立,此時(1)式無解。 情形四:若n-φ(φ(n))=18,則由引理4,知19≤n≤35,將其逐一代入驗證,經檢驗n=22滿足n-φ(φ(n))=18,即n=22為(1)式的解。 定理2 復合歐拉函數方程φ(n-φ(φ(n)))=8 (2)的正整數解:n=18,20,24,28,32。 證明:因為φ(n-φ(φ(n)))=8,所以n-φ(φ(n))=15,16,20,24,30,下面分5種情況加以討論: 情形一:若n-φ(φ(n))=15,則由引理4,知16≤n≤29,將其逐一代入驗證,經檢驗n-φ(φ(n))=15不成立,即此時(2)式無解。 情形二:若n-φ(φ(n))=16,則由引理4,知17≤n≤31,將其逐一代入驗證,經檢驗n=18,20滿足n-φ(φ(n))=16,即n=18,20為(2)式的解。 情形三:若n-φ(φ(n))=20,則由引理4,知21≤n≤39,將其逐一代入驗證,經檢驗n=24滿足n-φ(φ(n))=20,即n=24為(2)式的解。 情形四:若n-φ(φ(n))=24,則由引理4,知25≤n≤47,將其逐一代入驗證,經檢驗n=28,32滿足n-φ(φ(n))=24,即n=28,32為(2)式的解。 情形五:若n-φ(φ(n))=30,則由引理4,知31≤n≤59,將其逐一代入驗證,經檢驗n-φ(φ(n))=30不成立,此時(2)式無解。 定理3 復合歐拉函數方程φ(n-φ(φ(n)))=10 (3)的正整數解:n=15,26。 證明:因為φ(n-φ(φ(n)))=10,所以n-φ(φ(n))=11,22,下面分2種情況加以討論: 情形一:若n-φ(φ(n))=11,則由引理4,知12≤n≤21,將其逐一代入驗證,經檢驗n=15滿足n-φ(φ(n))=11,即n=15為(3)式的解。 情形二:若n-φ(φ(n))=22,則由引理4,知23≤n≤43,將其逐一代入驗證,經檢驗n=26滿足n-φ(φ(n))=22,即n=26為(3)式的解。 定理4 復合歐拉函數方程φ(n-φ(φ(n)))=12 (4)的正整數解:n=19,23,27,30,34,44,46,50。 證明:因為φ(n-φ(φ(n)))=12,所以n-φ(φ(n))=13,21,26,28,36,42,下面分6種情況加以討論: 情形一:若n-φ(φ(n))=13,則由引理4,知14≤n≤25,將其逐一代入驗證,經檢驗n=19,23滿足n-φ(φ(n))=13,即n=19,23為(4)式的解。 情形二:若n-φ(φ(n))=21,則由引理4,知22≤n≤41,將其逐一代入驗證,經檢驗n=27滿足n-φ(φ(n))=21,即n=27為(4)式的解。 情形三:若n-φ(φ(n))=26,則由引理4,知27≤n≤51,將其逐一代入驗證,經檢驗n=30,34滿足n-φ(φ(n))=26,即n=30,34為(4)式的解。 情形四:若n-φ(φ(n))=28,則由引理4,知29≤n≤55,將其逐一代入驗證,經檢驗n-φ(φ(n))=28不成立,即此時(4)式無解。 情形五:若n-φ(φ(n))=36,則由引理4,知37≤n≤71,將其逐一代入驗證,經檢驗n=44,46滿足n-φ(φ(n))=36,即n=44,46為(4)式的解。 情形六:若n-φ(φ(n))=42,則由引理4,知43≤n≤83,將其逐一代入驗證,經檢驗n=50滿足n-φ(φ(n))=42,即n=50為(4)式的解。 定理5 復合歐拉函數方程φ(n-φ(φ(n)))=16 (5)的正整數解:n=21,25,29,36,38,40,48,54,56,64。 證明:因為φ(n-φ(φ(n)))=16,所以n-φ(φ(n))=17,32,34,40,48,60,下面分6種情況加以討論: 情形一:若n-φ(φ(n))=17,則由引理4,知18≤n≤33,將其逐一代入驗證,經檢驗n=21,25,29滿足n-φ(φ(n))=17,即n=21,25,29為(5)式的解。 情形二:若n-φ(φ(n))=32,則由引理4,知33≤n≤63,將其逐一代入驗證,經檢驗n=36,38,40滿足n-φ(φ(n))=32,即n=36,38,40為(5)式的解。 情形三:若n-φ(φ(n))=34,則由引理4,知35≤n≤67,將其逐一代入驗證,經檢驗n-φ(φ(n))=34不成立,即此時(5)式無解。 情形四:若n-φ(φ(n))=40,則由引理4,知41≤n≤79,將其逐一代入驗證,經檢驗n=48滿足n-φ(φ(n))=40,即n=48為(5)式的解。 情形五:若n-φ(φ(n))=48,則由引理4,知49≤n≤95,將其逐一代入驗證,經檢驗n=54,56,64滿足n-φ(φ(n))=48,即n=54,56,64為(5)式的解。 情形六:若n-φ(φ(n))=60,則由引理4,知61≤n≤119,將其逐一代入驗證,經檢驗n-φ(φ(n))=60不成立,即此時(5)式無解。
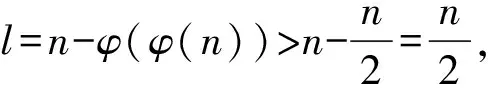
2 主要結論及其證明

