我國脫貧攻堅指標數據質量檢驗
——基于Benford法則和面板數據模型

吳繼英， 薛艷杰

數據是國家的基礎性戰略資源，對生產、流通和分配等方面產生越來越重要的影響。學術研究離不開數據，高質量的統計數據是國家制定宏觀政策的基礎，也是考核官員政績的重要依據。2021年2月習近平總書記在全國脫貧攻堅總結表彰大會上宣告我國脫貧攻堅戰取得了全面勝利，現行標準下9 899萬農村貧困人口全部脫貧。脫貧統計數據質量直接影響脫貧攻堅成果評價，從而引發社會各界關注。2020年初新冠疫情暴發，在脫貧工作完成的過程中，黨中央國務院不止一次地提出拒絕數字脫貧、虛假脫貧。然而，有部分地區為了彰顯政績、謀取國家扶貧項目和套取國家扶貧資金，在脫貧數據方面造假，虛報農戶收入水平、超報貧困人口數量、脫貧成效考核時更改貧困標準，導致數字脫貧與虛假脫貧現象時有發生(1)李曉園, 鐘偉. 大數據驅動中國農村精準脫貧的現實困境與路徑選擇[J].求實,2019(5):78-87.。在此背景下把好脫貧統計數據質量關，進行脫貧統計數據質量檢驗，能夠有效檢驗脫貧成果，為國家各級部門科學決策提供高質量的數據保障，使脫貧攻堅成果經得起歷史和人民的考驗，對我國進一步提升國際形象具有十分重要的意義。

一、 文獻綜述

統計數據質量檢驗一直是學術界關注的重點，檢驗的方法主要有邏輯關系檢驗法、調查誤差評估法、計量分析檢驗法、統計分布檢驗法、多維評估法等。Benford法則屬于統計分布檢驗法的一種，經過不斷發展完善逐漸成為檢驗數據質量的常用方法之一(2)韓兆洲, 程學偉. GDP統計數據質量實證研究: 基于Benford法則和空間面板模型[J]. 數理統計與管理, 2019,38(3):394-404.，最早應用于會計領域用來檢查會計相關行業統計數據的徇私舞弊行為(3)NIGRINI M J, MITTERMAIER L I. The use of Benford’s law as an aid in analytical procedures[J]. Auditing： a journal of practice & theory,1997,16(2):52-67.，后又逐漸應用于宏觀和微觀統計數據方面(4)許滌龍, 金瑛. 基于Benford法則的M2統計數據準確性研究[J]. 統計與信息論壇, 2010,25(8):20-24.，如檢驗調查數據質量(5)GEORGE J, LAURA S. Detecting problems in survey data using Benford’s law[J]. Journal of human resourus,2009,44(1):1-24.，檢驗GDP數據(6)曾五一, 薛梅林. GDP國家數據與地區數據的可銜接性研究[J]. 廈門大學學報(哲學社會科學版),2014(2):110-119.、保險行業相關數據(7)劉云霞, 曾五一. 關于綜合利用Benford法則與其他方法評估統計數據質量的進一步研究[J]. 統計研究, 2013,30(8):3-9.和宏觀經濟統計數據(8)米子川, 楊小慶. Benford法則: 中國宏觀經濟統計數據質量評價的一種新范式[J]. 數學的實踐與認識, 2014,44(24):10-18.的準確性等。亦有研究運用計量模型通過考察待評估指標與其他關聯性指標的匹配度進行數據質量檢驗(9)劉思明, 臧夢玲. 中國地區GDP增長數據準確度評估——納入太空燈光數據下修正“克強指數”的實證研究[J]. 云南財經大學學報, 2018,34(6):27-37.。Benford法則檢驗法多與計量模型結合使用，如劉云霞運用Benford法則和面板模型結合的方法對我國稅收收入進行質量檢驗(10)劉云霞, 吳曦明, 曾五一. 關于綜合運用Benford法則和面板模型檢測統計數據質量的研究[J]. 統計研究, 2012,29(11):74-78.、闕里和鐘笑寒對我國地區 GDP 增長的統計數據進行了真實性檢驗(11)闕里, 鐘笑寒. 中國地區GDP增長統計的真實性檢驗[J]. 數量經濟技術經濟研究, 2005(4):3-12.。

綜上所述，相關學者運用Benford法則和計量模型相結合對我國經濟統計數據質量進行檢測，為本文研究提供了良好的方法基礎，但現有研究構建計量模型時，未對解釋變量數據進行質量檢驗，容易造成檢驗結果的偏差性。因此，本文在構建面板數據模型之前，運用Benford法則對變量數據進行質量檢驗，同時為增加結果的可信度、避免單一方法檢驗所造成的誤差，引入邏輯匹配檢驗和殘差檢驗。現有檢驗數據質量的研究大多集中在對GDP等經濟統計指標的檢驗，關于脫貧攻堅方面的研究也更多傾向于扶貧成效的測度方面(12)周玉龍, 孫久文. 瞄準國貧縣的扶貧開發政策成效評估——基于1990—2010年縣域數據的經驗研究[J]. 南開經濟研究,2019(5):21-40.(13)聶君, 束錫紅. 青海藏區精準扶貧績效評價及影響因素實證研究[J]. 北方民族大學學報(哲學社會科學版), 2019,145(1):33-41.，對脫貧攻堅指標數據進行質量檢驗的研究成果幾乎未見。鑒于此，本文以2013—2018年我國農村地區(14)全國農村，涉及31個省份。和貧困地區(15)貧困地區：貧困地區包括集中連片特困地區和片區外的國家扶貧開發工作重點縣，主要涉及22個省。為便于比較，本文以省為單位進行研究。范圍內4個重要脫貧指標統計數據為研究對象，運用Benford法則對脫貧統計數據前兩位數字的真實性進行檢驗，并構建主成分面板回歸模型進行指標之間的邏輯匹配性檢驗，由回歸分析得到的殘差進一步檢測脫貧指標問題數據出現的時間和區域。

二、 方法介紹

(一) Benford法則

Benford法則認為數據集的各位數字存在著某種分布規律，通過比較理論頻率與實際頻率來檢驗數據質量。Benford法則經過現象發現——給出數學表達式——證明、推導，不斷發展和改善，已經成為檢測數據是否存在修飾、篡改和舞弊等質量問題的重要方法之一(16)龐新生, 廖子宜. 分市縣住戶調查收支匯總數據的準確性評估[J]. 統計與決策,2019,35(22):11-15.。依據Benford定律，首位數字(非零非負)出現的頻率為

(1)

第二位數字出現的頻率為

(2)

…

其中，d1是數據的首位數字，為1～9，該數字應非零非負，p(d1)是該首位數字d1出現的頻率；d2是數據的第二位數字，為0～9，該數字應非負，p(d2)是該第二位數字d2出現的頻率。

Benford法則首位數字和第二位數字分布的理論頻率如表1所示。

表1 Benford法則下首位數字和第二位數字分布的理論頻率

依據理論頻率分布可以發現：隨著首位和第二位數字的不斷增大，理論分布頻率不斷降低，且降低的幅度越來越小。高質量數據的數字分布應該符合Benford法則，如果數據存在人為調整、修改、修飾等行為，就會破壞這種規則(17)韓兆洲, 程學偉. GDP統計數據質量實證研究: 基于Benford法則和空間面板模型[J]. 數理統計與管理,2019,38(3):394-404.。Benford法則常用的檢驗方法主要有χ2擬合優度檢驗、修正的K-S擬合優度檢驗、距離檢驗和Pearson相關系數檢驗。

(二) 面板數據模型

Benford法則雖然可以從一定程度上檢驗問題數據出現的位數，但卻無法準確地識別出問題數據出現的具體時間與地區，此外也容易受到樣本數量的影響，單靠Benford法則無法確定統計數據是否真的存在質量問題，將其與面板數據模型結合，既可以很好地規避這一缺點，又可以很好地避免由于模型設定和變量選取的不同所導致的檢驗結果差異性。面板數據模型主要分為固定效應模型、隨機效應模型和混合回歸模型。其中，固定效應模型即假定每個個體回歸方程具有相同的斜率，每個個體的截距項不同。具體形式如下：

yit=ui+b*xit+eit，i=1,…，n;t=1,…，T

(3)

其中，i表示每個研究個體，t表示研究時期。yit是被解釋變量，xit是隨個體與時間而改變的解釋變量；ui是不隨時間而變的個體特征，eit是隨個體與時間而改變的擾動項。

三、 基于Benford法則的脫貧指標統計數據實證研究

(一) 指標選取與數據預處理

為保證脫貧統計數據質量的全面性與針對性，采用Benford法則分別對全國農村和貧困地區的脫貧統計數據前兩位數字進行質量檢驗，既能檢驗全國脫貧數據的質量狀況，又能有針對性地檢測貧困地區的脫貧數據質量。數據來源于《中國農村貧困監測報告》中2013—2018年31個省(市、自治區)總的貧困數據以及貧困地區的數據。

在政府工作報告以及相關會議政策中，論述脫貧攻堅成效時都明確提到了貧困人口數、貧困發生率、人均可支配收入和人均消費支出等指標，這四項指標是考察脫貧攻堅成效的常用指標。貧困人口數、貧困發生率直接反映開展脫貧工作后的直接成果，人均可支配收入反映居民的基本生活保障度，人均消費支出反映了農村居民及貧困地區的消費能力。對這四項指標進行統計數據質量檢驗分析，對于衡量脫貧工作的真實成效具有重要的意義。鑒于此，本文最終選取貧困人口數(萬人)、貧困發生率(%)、農村居民人均可支配收入(元)和人均消費支出(元)四項指標作為數據質量檢驗的基礎性指標。

運用Benford法則需要滿足四個基本條件：一是數據受主觀因素影響較小且數據量較大，樣本量一般大于等于100；二是數據從不同來源隨機抽樣，無人為限制；三是數據是自然形成的，不可人為賦值；四是首位數字非零非負，同時無最大值與最小值的限制，不能按一定規律排序。結合所選樣本指標數據的特征(如《中國農村貧困監測報告》給出的貧困發生率數據大多為兩位數字)，對樣本數據的前兩位數字進行Benford法則驗證，同時對不符合上述條件的數據進行處理，使其保留原始數據信息的基礎上適合運用Benford法則(18)劉明宇. 基于Benford法則的城鎮居民人均可支配收入質量評估[J]. 統計與咨詢,2014(6):30-31.。

由于貧困人口數指標單位為萬人，導致個別省份貧困人口數只有一位數字，對這樣的數據一般至少乘以10。貧困發生率(%)指標個別省份數據小于百分之1或只有一位數字，將該指標樣本數據值乘以100。為計算方便，將全國農村和貧困地區的這兩項指標(貧困發生率和貧困人口數)的數據統一乘以100，得到符合要求的數據，該處理不影響Benford法則運算結果。另外，由于當部分省份某個指標某一年的數據較小而被忽略不計導致該指標數據缺失時，比如，在計算全國農村脫貧指標數據的理論頻率時，北京(2013—2018)、天津(2013—2018)、上海(2013)、江蘇(2015—2018)、浙江(2015—2018)、福建(2017—2018)、山東(2018)、廣東(2016—2018)的貧困人口數和貧困發生率數據較小而缺失，在計算該類指標首位數字和第二位數據出現次數時，不考慮該指標上述省份上述年份的數據，在計算總數時也予以刪除。經上述處理，得到符合要求的樣本數據。

(二) 指標數據前兩位數字頻率分布

對處理后符合要求的樣本數據，首先提取全國農村及貧困地區4個指標的首位和第二位數字；其次計算首位數字1～9和第二位數字0～9出現的次數，然后分別利用次數除以總次數，計算出首位數字1～9和第二位數字0～9出現的實際頻率；最后將實際頻率與Benford理論頻率進行對比計算差異值，并對可能存在的差異是否顯著進行χ2檢驗以判定脫貧指標的數據質量。

全國農村和貧困地區“貧困發生率”“農村貧困人口”“農村居民人均可支配收入”和“農村居民人均消費支出”四項指標數據，首位數字出現0～9和第二位數字出現1～9的實際頻率、Benford法則下的理論頻率以及二者之間的差異分別如表2所示(限于篇幅，其他3個指標的結果略)。

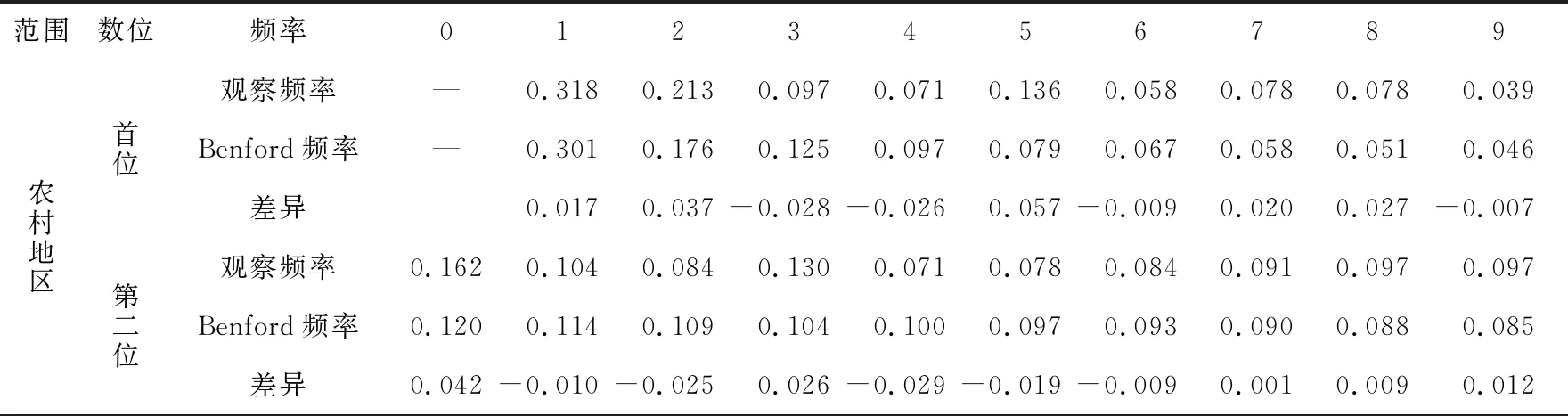
表 2 “貧困發生率”數據的實際頻率、理論頻率及差異

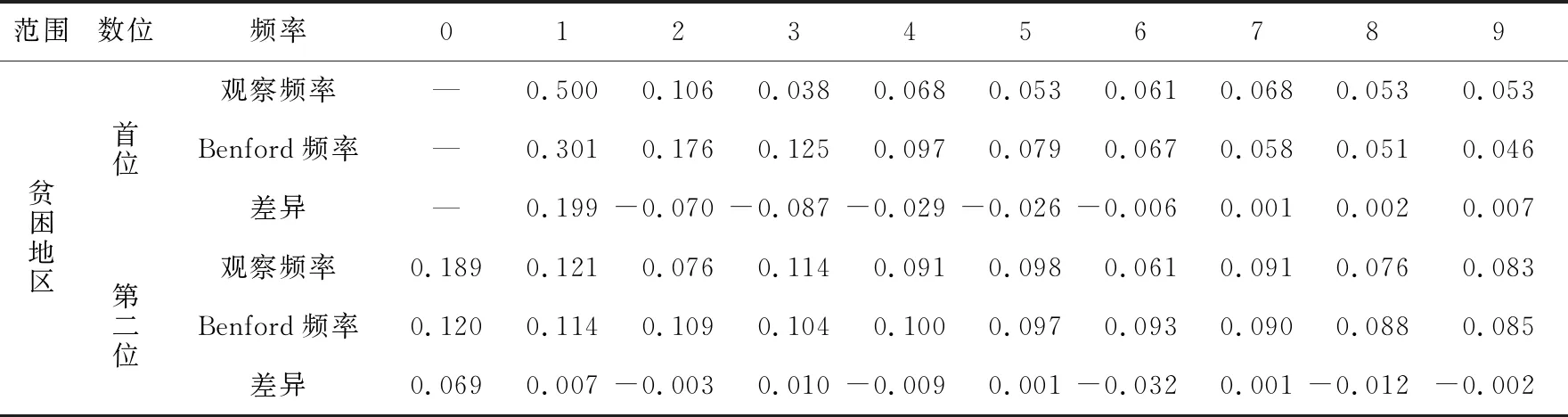
續表

由表2可知，貧困發生率指標的全國農村和貧困地區數據首位數字出現的實際頻率除個別數值外，整體呈遞減趨勢；而全國和貧困地區數據第二位數字出現的實際頻率分布趨勢卻未呈現依次遞減趨勢，分布趨勢呈上下波動。進一步觀察二者首位與第二位數字出現的實際頻率與Benford法則下理論頻率差異的絕對值，除個別值(貧困地區的貧困發生率首位數字為1、3、2，貧困地區第二位數字為0)較大以外，整體較小。

貧困人口數指標的全國農村數據首位數字除6以外，貧困地區數據首位數字除6和7的實際頻率外，整體呈遞減趨勢；而第二位數字兩者都時增時減，未呈現明顯遞減趨勢的規律。二者首位數字與第二位數字出現的實際頻率與Benford法則下理論頻率差異的絕對值較小。

農村居民人均可支配收入指標的全國農村數據的首位數字之間呈現先減(1～4)后增(5～9)趨勢，貧困地區除數字2、3、6以外，數字分布頻率隨著數字的增大逐漸呈遞減趨勢；第二位數字全國地區和貧困地區數字0～5出現頻率隨著數字的增大遞減，之后遞減趨勢消失。全國地區首位數字出現的實際頻率與Benford法則下理論頻率差異的絕對值個別數值較大，貧困地區首位數字出現的實際頻率與Benford法則下理論頻率差異的絕對值相對較大，第二位數字差異相對較小。

農村居民人均消費支出指標的全國農村和貧困地區數據的首位數字出現1～9的頻率先遞減后遞增再減；全國農村第二位數字除4、5、8、9以外呈現遞減趨勢，貧困地區數據中數字0～9出現的頻率沒有明顯呈現隨數字增大而遞減。全國農村和貧困地區首位數字出現的實際頻率與Benford法則下理論頻率差異的絕對值均比較大，而第二位數字實際頻率與理論頻率差異較小。

綜合來看，四項指標數據的首位數字與第二位數字實際頻率分布趨勢，與Benford法則下隨著數字增大而減小的理論頻率分布趨勢不一致，且有部分指標出現上升趨勢。除農村居民人均可支配收入和人均消費支出首位數字外，其他指標數據首位與第二位數字實際頻率與理論頻率差異相對較小。判斷數據是否符合Benford法則，還需進行χ2擬合優度檢驗。

(三) Benford法則檢驗

對貧困發生率等4個指標的計算結果進行χ2擬合優度檢驗，如果χ2統計量小于臨界值，則接受原假設(實際頻率與理論頻率之間無差異)，拒絕備擇假設，認為該統計數據符合Benford法則，數據準確性較高，人為篡改的可能性較小；如果χ2統計量大于臨界值，則拒絕原假設，接受備擇假設，即認為該樣本數據不符合Benford法則，數據存在造假的可能。

χ2統計量計算公式為

(4)

其中，ei為首位(第二位數字)出現的實際頻率，bi為Benford法則下首位(第二位)數字出現的理論頻率，N為樣本總量。在5%的顯著性水平下，首位數字和第二位數字的χ2統計量的臨界值分別為15.51、16.92(19)劉云霞, 吳曦明, 曾五一. 關于綜合運用Benford法則和面板模型檢測統計數據質量的研究[J]. 統計研究,2012,29(11):74-78.。

依據公式(4)，得到如表3所示的檢驗結果。

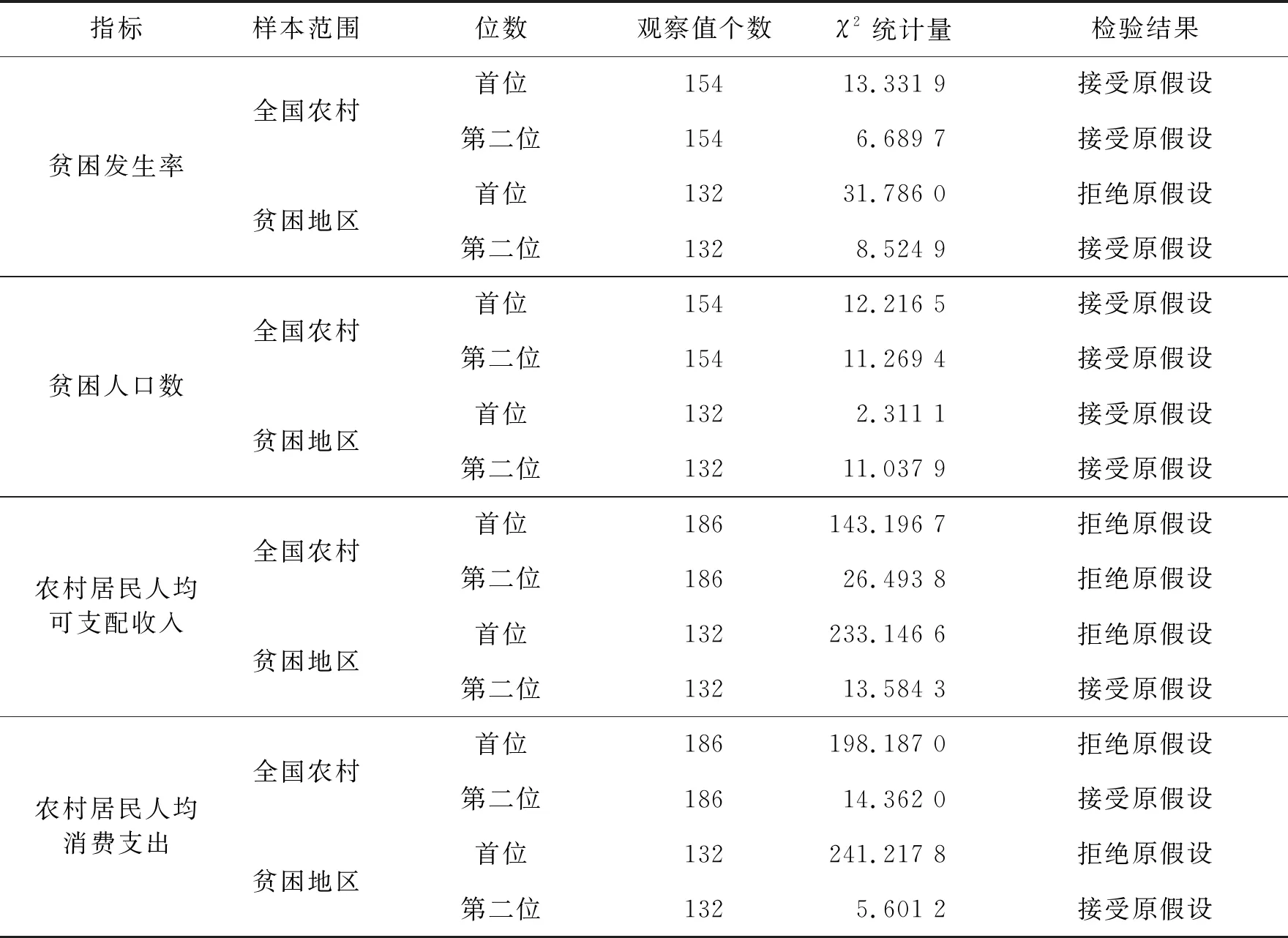
表3 四項脫貧指標數據前兩位數字分布的檢驗結果

由表3可知，2013—2018年全國農村脫貧指標中的貧困發生率、貧困人口數符合Benford法則，首位和第二位數字真實可信；貧困地區貧困人口數符合Benford法則，首位和第二位數字真實可信。此外，全國農村居民人均消費支出的第二位數字和貧困地區貧困發生率、農村居民人均可支配收入、農村居民人均消費支出的第二位數字的χ2檢驗結果也是接受原假設，表明上述指標第二位數字是真實可信的。2013—2018年全國農村居民人均可支配收入的首位和第二位數字、農村居民人均消費支出首位數字以及貧困地區的貧困發生率、農村人均可支配收入、農村居民人均消費支出的首位數字χ2檢驗結果均拒絕原假設，可認為上述指標相應位數的數字不符合Benford法則，可能存在數據質量問題。原因可能是不同省份指標之間的統計口徑或核算角度存在差異，也可能是由于所選擇的樣本時期較短、樣本量相對較少造成的。隨著我國經濟增長，人均可支配收入和人均消費支出也逐漸增長，指標數值變大造成這兩項指標數據中首位數字中某些數字(通常是較小的數字)缺失。同時由于政府對脫貧的有效治理也會導致貧困地區的貧困發生率的首位數字集中于某個數字，從而出現不符合Benford規律的現象。以貧困地區的貧困發生率指標為例，結合表2中的計算結果可知實際頻率比Benford理論頻率大的首位數字為1、7、8、9，表明該指標出現質量問題的數據大概率會出現在首位數字為1、7、8、9的數據中，也即貧困發生率過低或過高均應引起注意，在檢查數據質量時應該密切關注這些數據。

四、 基于面板數據模型的脫貧攻堅統計數據質量檢驗

由上述分析可知，無論是全國農村還是貧困地區，考察脫貧工作的直接指標“貧困發生率”的第一位數字均未通過統計檢驗，故需借助面板數據模型展開指標之間的邏輯匹配性檢驗，以進一步檢驗指標數據質量。由表3可知，全國農村范圍內的農村居民人均可支配收入指標首位和第二位均未通過檢驗，可能存在質量問題，因此不適合作為解釋變量構建面板數據模型。而貧困地區4個指標數據的第二位數字均通過了統計檢驗，整體數據質量相對較好，可以作為面板數據模型檢驗的樣本。同時考慮到貧困地區作為脫貧攻堅戰的主戰場，相關指標數據質量直接影響國家脫貧政策的制定。因此，針對貧困地區的各項指標構建面板數據模型進行邏輯匹配性檢驗和殘差檢驗。

(一) 變量的確定與數據處理

“貧困發生率”能夠較好地反映不同時期不同地區的貧困狀況，是衡量脫貧成效最重要的指標之一，故將其作為被解釋變量。“貧困人口數”是貧困發生率的直接關聯指標，考慮到貧困發生率與貧困人口數存在著一定的比例關系，選擇貧困人口數x1對貧困發生率進行邏輯匹配性檢驗是合理的，可以驗證二者的邏輯關系是否正確，故將其作為解釋變量；同時選取“人均可支配收入x2”“人均消費支出x3”作為解釋變量，通過構建面板模型進行邏輯匹配性檢驗。

為避免多重共線性需要對3個解釋變量提取主成分，傳統的主成分分析法對面板數據不適用，需采取全局主成分法；同時為了不減少數據信息量，提取與解釋變量數量相同的主成分，與被解釋變量進行回歸。由于提取主成分時對原始解釋變量進行了標準化處理，為保證一致性，對被解釋變量“貧困發生率”也進行標準化處理。運用SPSS 23.0進行全局主成分提取，具體過程略。

(二) 面板模型估計

首先需要選擇適當的模型進行回歸。采用stata軟件分別進行混合模型回歸、固定效應回歸和隨機效應回歸，然后利用F檢驗、LM檢驗和Hausman檢驗進行模型選擇，最終拒絕混合效應回歸模型和隨機效應回歸模型，選取固定效應回歸模型。經檢驗，隨機擾動項存在組間異方差、組內自相關和同期截面相關，因此采用FGLS對模型進行估計，得到回歸系數估計結果如表4所示。

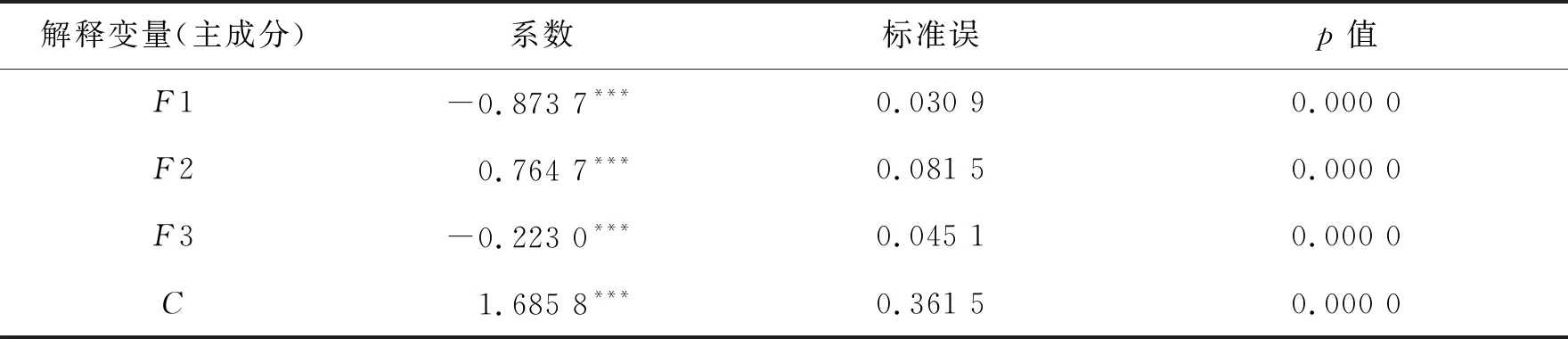
表4 個體固定效應回歸系數估計結果

由表4可知，模型中解釋變量F1、F2、F3的回歸系數均通過了1%顯著性水平檢驗，表明固定效應模型估計效果良好，所選取的自變量與因變量適合模型估計，接下來利用回歸結果進行邏輯匹配性檢驗。

(三) 基于面板模型的邏輯匹配性檢驗

主成分變量雖然可以消除共線性，但是卻無法很好地對被解釋變量進行解釋。因此需要把主成分與被解釋變量之間的回歸系數還原成原始變量與因變量之間的回歸系數。依據主成分的生成原理與表4，還原出因變量貧困發生率與原始自變量貧困人口數、農村居民人均可支配收入之間的回歸系數，如表5所示。

表5 還原后的回歸系數

表5中貧困人口數與貧困發生率之間呈正向關系，表明貧困人口數越多，貧困發生率越高；農村居民人均可支配收入、人均消費支出與貧困發生率呈負向關系，表明農村居民人均可支配收入和人均消費支出越高，貧困發生率相應越低。從貧困發生率與貧困人口數計算關系來看，模型中得出的二者之間存在正向相關關系合理，隨著國家扶貧政策投入的不斷深入，貧困地區得到救助的人數越來越多，貧困人口不斷減少，使得貧困發生率也逐漸降低。從社會發展規律和經濟發展過程來看，農村人均可支配收入、人均消費支出與貧困發生率存在負向關系合理，因為這兩項指標反映了農村居民的收入能力和消費能力，隨著精準扶貧政策和措施的不斷完善，國家扶貧產業不斷發展，貧困地區的勞動力資源得到開發利用，農民有了收入來源和消費基礎，生活水平逐漸提高，貧困發生率自然逐漸降低。因此，貧困發生率指標2013—2018年數據通過了邏輯匹配性檢驗，符合計算法則和社會發展規律。

(四)基于面板數據模型的殘差檢驗

經過Benford法則檢驗和邏輯匹配性檢驗可知，所選取的脫貧攻堅指標2013—2018年數據整體質量較好，但個別省份個別年份的數據還存在質量問題，可利用殘差的標準化值來揭示貧困發生率數據的異常值點。

殘差標準化計算公式如下：

(5)

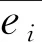
依據公式(5)計算2013—2018年貧困地區22個省貧困發生率的標準化殘差值見表6。

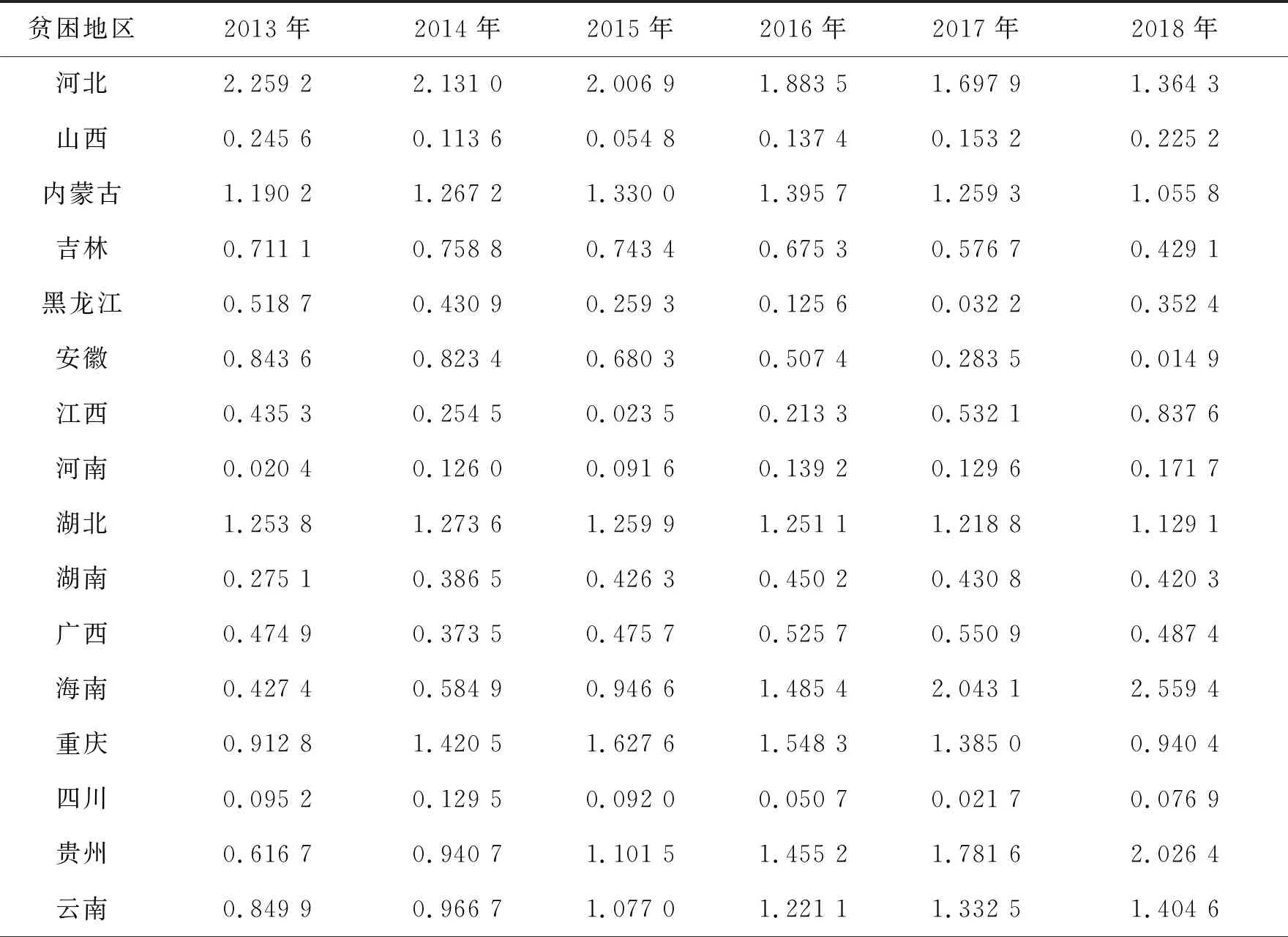
表6 貧困地區貧困發生率的標準化殘差值

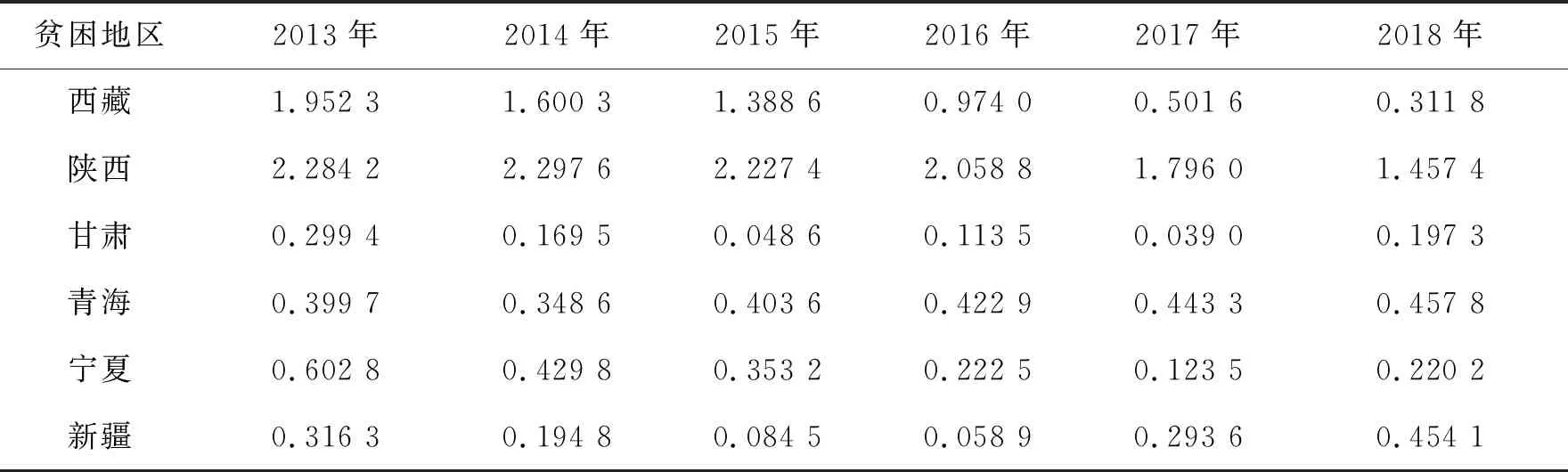
續表

由表6可知，河北省2013—2015年、海南省2017—2018年、貴州省2018年和陜西省2013—2016年的標準化殘差值大于2，為“異常數據”，其余地區均控制在2以內，說明上述省份的貧困縣在上述年份的貧困發生率數據可能存在質量問題。進一步觀察發現，河北省2016—2017年、重慶市2015—2016年、貴州省2017年、西藏2013—2014年、陜西2017年的標準化殘差值雖然小于2，但均大于1.5，有些數值已達到1.9，非常接近于2，可將這類數據歸為“瀕臨異常數據”處理，認為這些數據可能存在質量問題，應引起重視。值得注意的是，海南省和貴州省下屬貧困縣貧困發生率的標準化殘差值呈逐年遞增趨勢，應引起預警。

為避免由于模型設定和變量選取導致殘差檢驗結果出現不一致性，將Benford法則中理論頻率與實際頻率的差異值與殘差檢驗結果相結合來進一步確定上述問題數據。Benford法則檢驗結果顯示貧困發生率數據首位數字不服從Benford分布，表2顯示首位數字理論頻率與實際頻率的差異最大的首位數字為1，其次為3和2。殘差檢驗結果揭示問題數據(包括異常數據和瀕臨異常數據)共計18個，這18個問題數據中有7個數據(河北2014—2016年、陜西2013—2016年)的首位數字為1，1個數據(海南2018年)首位數字為3，2個數據(河北2013、西藏2013年)的首位數字為2，與Benford法則檢驗結果相符合。由此可見，這10個數據既是殘差檢驗下的問題數據，又是Benford檢驗下的問題數據，可認定這10個數據存在質量問題。其他8個問題數據雖然與Benford法則中理論頻率與實際頻率最大差異值所在的首位數字結果不一致，但仍可以確定貧困發生率指標個別省份與年份的統計數據可能存在質量問題。整體而言，貧困地區22個省2013—2018年共132個數據，結合殘差檢驗與Benford檢驗結果得到貧困發生率指標數據異常率為7.6%，可認為我國貧困地區的貧困發生率指標數據質量總體較好。

五、 結論

本文選取我國農村及貧困地區范圍內貧困人口數、貧困發生率、農村居民人均可支配收入和人均消費支出四個最常用的脫貧攻堅指標，首先利用Benford法則對指標統計數據的前兩位數字的分布規律進行檢驗；其次運用面板數據模型，以貧困發生率為因變量，由全局主成分法生成3個主成分為自變量構造個體固定效應模型，對四個脫貧攻堅指標的數據進行邏輯匹配性驗證，最后由回歸模型得到的殘差進行殘差檢驗。區別于單一方法檢驗，將Benford法則、邏輯檢驗和殘差檢驗三種方法相結合對我國2013—2018年的脫貧指標數據質量進行檢驗，減小了檢驗結果偏差，使檢驗結果更具可信性。研究成果豐富了脫貧統計相關理論與方法，能夠針對虛假脫貧與數字脫貧現象提供預警，為國家相關部門政策的制定提供高質量的數據保障。研究得到以下結論：

1. Benford法則的χ2擬合優度檢驗結果顯示，全國農村和貧困地區范圍內的脫貧統計數據質量相差不大。全國農村的貧困發生率和貧困人口數首位數字和第二位數字、農村居民消費支出的第二位數字、貧困地區貧困發生率、貧困人口數首位數字和第二位數字、農村居民人均可支配收入以及人均消費支出的第二位數字均通過了統計檢驗，說明從統計檢驗角度來看，數據質量良好，數據真實可信，不存在人為竄改的可能；全國范圍內農村居民人均可支配收入的首位和第二位數字、貧困地區范圍內的貧困發生率、人均可支配收入和人均消費支出的第一位數字未通過統計性檢驗，認為該數據存在質量問題。出現這種結果可能是所選擇的樣本時期過短、樣本總量過少，使樣本數據的首位過于集中于某位數字造成的，也可能是因為統計口徑或核算角度的差異造成的，真實原因有待進一步探索和檢驗。

2. 基于固定效應面板模型的邏輯匹配性檢驗結果顯示，貧困地區范圍內，貧困人口數與貧困發生率之間呈正向相關關系，農村居民人均可支配收入和人均消費支出與貧困發生率呈負向相關關系，通過邏輯性匹配檢驗。

3. 對固定效應面板模型的殘差檢驗結果表明，2013—2018年貧困地區大部分省份下屬貧困縣的貧困發生率數據通過了殘差檢驗，共計18個統計數據可能存在質量問題，結合Benford檢驗結果發現這18個問題數據中有10個數據既是殘差檢驗的問題數據，又是Benford法則檢驗的問題數據。殘差檢驗與Benford檢驗結合所顯示貧困發生率數據的異常率為7.6%。

綜合來看，無論是Benford檢驗、邏輯檢驗還是殘差檢驗，以全國農村或是貧困地區為統計范疇，所選取的脫貧攻堅四個常用統計指標2013—2018年期間整體數據質量良好。但仍有個別指標和個別地區的數據存在問題，為提高我國脫貧攻堅方面統計數據質量，本研究提出以下建議：

第一，對全國農村居民人均可支配收入2013—2018年的數據予以關注，探究其未通過統計分布檢驗的真實原因。同時對河北2014—2016年、陜西2013—2016年、海南2018、河北2013、西藏2013年下屬貧困縣的貧困發生率數據進行核查，看是否存在數據造假行為。2021年我國脫貧工作取得了舉世矚目的成就，實現全面脫貧，在國際國內高度關注下更應加大脫貧統計數據的核查力度，保證統計數據的真實性不被破壞，從而使我國脫貧攻堅成果經得起歷史和人民的考驗。

第二，統一相關指標數據核算口徑，明確核算范圍。例如統一農村居民可支配收入口徑和核算范圍，從而使得不同地區收入數據具有可比性，減少因口徑不統一導致的數據失真現象發生。

第三，完善脫貧攻堅數據庫系統。利用大數據技術，實時跟蹤貧困地區貧困情況，建立和完善脫貧統計大數據倉庫，實行動態管理模式，有效防范“虛假脫貧”“數字脫貧”現象發生。同時加大扶貧統計數據監管制度，完善相關法律法規，對數據造假行為予以法律約束和懲戒，維護黨和政府的良好形象，為考察脫貧成效提供高質量的統計數據，為國家制定合理有效的脫貧政策提供科學依據。