對(duì)數(shù)預(yù)不變凸模糊映射及其應(yīng)用

白玉娟

（隴東學(xué)院 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，甘肅 慶陽(yáng) 745000）

眾所周知，凸性理論在對(duì)策論、工程、管理科學(xué)和最優(yōu)化理論中起著非常重要的作用。然而，許多實(shí)際問(wèn)題形成的數(shù)學(xué)模型，常常不能滿(mǎn)足凸規(guī)劃的基本要求，于是出現(xiàn)了對(duì)各種各樣的廣義凸性以及與數(shù)學(xué)規(guī)劃問(wèn)題相關(guān)聯(lián)的一些基本性質(zhì)的研究。1981 年，Hanson 提出了不變凸函數(shù)的定義并將其推廣為擬不變凸和偽不變凸[1]。1988 年，Weir T 和Mond B 提出預(yù)不變凸函數(shù)的定義，并研究了此類(lèi)函數(shù)在最優(yōu)化中的應(yīng)用[2]。2001 年，楊新民給出了預(yù)不變凸函數(shù)的其他性質(zhì)[3]，隨后顏麗佳提出了強(qiáng)預(yù)不變凸函數(shù)[4]。具體的優(yōu)化問(wèn)題數(shù)學(xué)建模過(guò)程中，往往還需要模糊數(shù)描述不確定參數(shù)，因此，關(guān)于模糊凸分析理論與其相對(duì)應(yīng)的模糊優(yōu)化問(wèn)題的研究，引起了廣大學(xué)者的興趣。1994 年，NOOR M A 給出了預(yù)不變凸模糊映射和模糊不變凸集的概念[5]。1999 年，SYAU Y R 定義了η為向量值函數(shù)的預(yù)不變凸性，得到預(yù)不變凸模糊映射的兩個(gè)刻劃定理，并討論了其在優(yōu)化理論中的應(yīng)用[6]。1992 年，Nanda S 提出了對(duì)數(shù)凸模糊映射[7]。2006 年，張成利用模糊數(shù)的表示定理，證明了對(duì)數(shù)凸模糊映射一些基本性質(zhì)[8-9]。本文提出對(duì)數(shù)預(yù)不變凸模糊函數(shù)的概念，討論對(duì)數(shù)預(yù)不變凸模糊函數(shù)的若干性質(zhì)及此類(lèi)函數(shù)在模糊數(shù)學(xué)優(yōu)化問(wèn)題中的應(yīng)用。

1 預(yù)備知識(shí)

定義1[10]56記E=且滿(mǎn)足：

（1）u是上半連續(xù)的；

（2）u是正規(guī)的，即存在x0∈R，使得u(x0)=1；

（3）u是凸模糊集，即對(duì) ?x,y∈R，α∈[0,1]，有u(αx+(1-α)y) ≥min{u(x),u(y)}；

（4）[u]0=cl{x∈R:u(x)＞ 0}是緊集。

任意的u∈E，u被稱(chēng)為模糊數(shù)且E稱(chēng)為模糊數(shù)空間。顯然，任意的u∈E，α∈[0,1]，

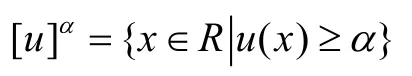
是非空有界閉集。

定理1[10]58設(shè)u∈E，則u-(α)與u+(α)是[0,1]上的函數(shù)且滿(mǎn)足：

（1）u-(α)單調(diào)非降左連續(xù)；

（2）u+(α)單調(diào)非增左連續(xù)；

（3）u-(α)，u+(α)在處是右連續(xù)的；

（4）u-(α)≤u+(α)。

反之，對(duì)任何滿(mǎn)足上述條件(1)-(4)的函數(shù)u-(α)，u+(α)，存在唯一的u∈E，使得

定義2設(shè)u,v∈E，對(duì)于任意的α∈[0,1]，如果

即u-(α)≥v-(α)且u+(α)≤v+(α)，則稱(chēng)。稱(chēng)u=v當(dāng)且僅當(dāng)且

對(duì)u∈E，當(dāng)且僅當(dāng)

稱(chēng)u為零模糊數(shù)，記作

定義3設(shè)集合I(?R)，如果存在一個(gè)向量函數(shù)η:R n×Rn→Rn，使得對(duì) ?t,t'∈I,?λ∈[0,1]滿(mǎn)足t'+λη(t,t')∈I，則集合稱(chēng)I(?R)是不變凸集。

定義4設(shè)I(?R) 為一個(gè)不變凸集，一個(gè)模糊映射f:I→E稱(chēng)為預(yù)不變凸模糊映射當(dāng)且僅當(dāng)：對(duì)?t,t'∈I,?λ∈[0,1]，有

2 對(duì)數(shù)預(yù)不變凸模糊映射及其應(yīng)用

定理2[11]設(shè){a(α),b(α)}(0≤α≤ 1)是R上的一族非空有界閉區(qū)間且滿(mǎn)足：

（1）[a(α2),b(α2)] ?[a(α1),b(α1)]，對(duì)所有的0＜α1≤α2；

（2）對(duì)任何非減列{αk} ?[0,1],α k↑α，有

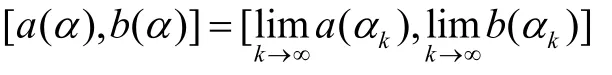
則[a(α),b(α)]為某一模糊數(shù)A的截集；反之，若[a(α),b(α)]為某一模糊數(shù)A的截集，則必須滿(mǎn)足條件（1）和（2）。

由0＜A-(α)≤A+(α)，得

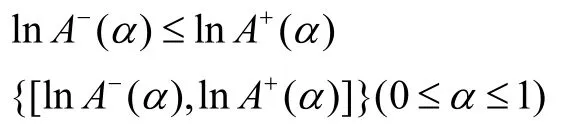
為R上的一族非空有界閉區(qū)間。

因?yàn)楫?dāng)(0≤α1≤α2)時(shí)，

所以

如果對(duì)于任何非負(fù)遞減

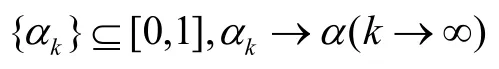
有

根據(jù)對(duì)數(shù)函數(shù)的連續(xù)性，得

于是由定理2 可知，

表示一個(gè)對(duì)數(shù)模糊數(shù)。

定理3設(shè)A,B∈E+，若A≥B，則有

（1）lnA≥lnB；

（2）Aα≥Bα(α＞ 0)。

定義5 設(shè)I?R為不變凸集，f:I→E+為定義在I上的模糊映射。

（1）若對(duì) ?t,t'∈I,?λ∈[0,1]，有

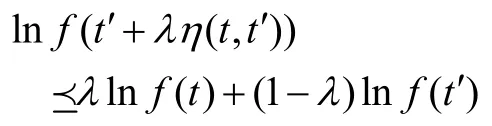
則稱(chēng)f是對(duì)數(shù)預(yù)不變凸的。

（2）若對(duì) ?t,t'∈I,t≠t',?λ∈[0,1]，有

則稱(chēng)f是嚴(yán)格對(duì)數(shù)預(yù)不變凸的。

定理4設(shè)I?R為不變凸集，f:I→E為模糊映射，則f為I上的預(yù)不變凸函數(shù)的充要條件為：對(duì)任給的α∈[0,1]，f-(x,α),f+(x,α)均為I上的預(yù)不變凸函數(shù)。

定理 5設(shè)I?R為不變凸集，若模糊映射f:I→E+為對(duì)數(shù)預(yù)不變凸的，則模糊映射f為預(yù)不變凸的。

證明因?yàn)?/p>

所以 -lnx為凸函數(shù)，從而對(duì)a＞0,b＞ 0，(a,b∈R)，λ∈[0,1]，有

即

設(shè)

為I上的對(duì)數(shù)預(yù)不變凸模糊映射，則對(duì)任意的x,y∈I及任意的λ∈[0,1]，有

根據(jù)模糊數(shù)對(duì)數(shù)定義，對(duì)任意α∈[0,1]，有

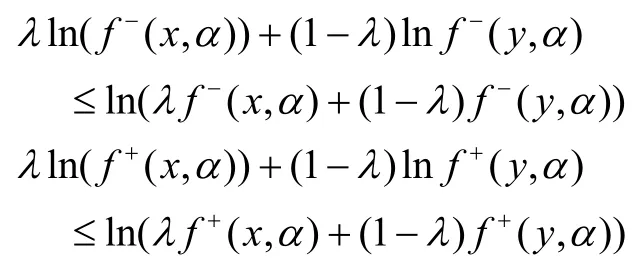
從而，有

這說(shuō)明，對(duì)任意的α∈[0,1]，f-(x,α),f+(x,α)均為預(yù)不變凸函數(shù)，f為預(yù)不變凸模糊映射。

3 對(duì)數(shù)預(yù)不變凸模糊數(shù)值函數(shù)與優(yōu)化問(wèn)題

對(duì)于求模糊數(shù)值函數(shù)f:I→E+的非約束模糊優(yōu)化問(wèn)題記為：

Minimizef(t)，Subject to t∈I。

定義6設(shè)I?R關(guān)于η:R×R→R是不變凸集，f:I→E+為I上的模糊數(shù)值函數(shù)，t0∈I，

（1）若存在t0的某個(gè)鄰域N(t0)，當(dāng)t∈I∩N(t0)有則稱(chēng)t0為f的局部最優(yōu)解。

（2）若對(duì)?t∈I有則稱(chēng)t0為f的全局最優(yōu)解。

定理 6設(shè)I?R為不變凸集，若模糊映射f:I→E+為對(duì)數(shù)預(yù)不變凸的，則f的局部最優(yōu)解必為全局最優(yōu)解。

證明設(shè)x0為f在I上的局部最小值點(diǎn)。若x0不是全局最小值點(diǎn)，則存在y0使得f(y0)＜f(x0)，由于模糊映射f為對(duì)數(shù)預(yù)不變凸的，即對(duì)任意的λ∈[0,1]，有

定理7設(shè)I?R為非空不變凸集，若模糊映射f為對(duì)數(shù)預(yù)不變凸的，Ω 為f的全局最優(yōu)解的集合，則Ω 也是關(guān)于η的不變凸集。

證明?x,y∈Ω，由于Ω 為f的全局最優(yōu)解的集合，于是

又模糊映射f為對(duì)數(shù)預(yù)不變凸的，即對(duì)任意的λ∈[0,1]有，

又因?yàn)閤是全局最優(yōu)解，所以

故Ω 是關(guān)于η的不變凸集。

定理8設(shè)I?R為非空不變凸集，若模糊映射f為嚴(yán)格對(duì)數(shù)預(yù)不變凸的，則f在I上的全局最小值點(diǎn)是唯一的。

證明設(shè)x0為全局最小值點(diǎn)，y0也為最小值點(diǎn)且x0≠y0，則

因?yàn)槟：成鋐為嚴(yán)格對(duì)數(shù)預(yù)不變凸的，即對(duì)任意的λ∈[0,1]，有

這與x0是f在I上的全局最小值點(diǎn)矛盾，故f在I上的全局最小值點(diǎn)是唯一的。

定理9設(shè)I?R為非空不變凸集，若模糊映射f為對(duì)數(shù)預(yù)不變凸的，則水平集合

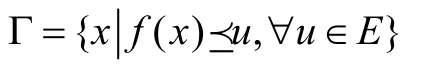
為不變凸集。

證明?x,y∈Γ，都有，即

因?yàn)槟：成鋐為對(duì)數(shù)預(yù)不變凸的，即對(duì)任意的λ∈[0,1]有，

故Γ為不變凸集。