基于數學文化課程的思政元素案例分析

劉建波，陳子越，張艷艷

（東北大學秦皇島分校 數學與統計學院，河北 秦皇島 066004）

1 數學文化與思政教育的“交”與“融”

1.1 什么是數學文化？

談及數學，很多人認為它是數字、公式，邏輯推理的堆砌，更多地是把數學當成一種工具。但在文化的歷史長河中抹不去數學的存在，唐代詩人李白的“孤帆遠影碧空盡，唯見長江天際流”從文學角度表達了對友人的留戀之情；從數學的角度看，“帆影”“碧空盡”體現了隨著距離的越遠而看不見船帆，反映出了無窮小量的重要概念。魏晉時期數學家劉輝的割圓術，“割之彌細，所失彌少，割之又割，以至于不可割，則與圓合體而無所失矣”，這詮釋了分割的思想，為數列極限的定義以及定積分的引入奠定了基礎[1]。數學文化不僅是歷史的產物，還是無數數學家、科學家的勞動和智慧的結晶。廣義上講，數學文化還包括數學家、數學史、數學美、數學教育以及教學發展中的人文成分，是指數學的思想、精神、方法、觀點以及它們的形成和發展[2]1-3。

1.2 課程思政不是思政課程

課程思政是教書育人的基本表達途徑，回答了“怎樣培養人”這一實踐性問題，這個問題是教育的關鍵問題。而思政課程是用政治講政治，體現了教育的首要問題是“培養什么樣的人”。學校是國家培養人才的重要基地，所有課程都有育人功能，要以“德育”為抓手，堅持把立德樹人作為中心環節，把思想政治工作貫穿教育教學全過程，推動“思政課程”與“課程思政”同向同行，形成協同效應[3]。課程思政的過程是價值理論和工具理論的統一，將思想政治教育和專業知識、活動經驗融合，課程是思政的載體，思政是課程的內涵。課程思政的價值是合目的性、合規律性與合必然性的統一，合目的是“培養什么樣的人”，需要圍繞著專業培養目標和課程培養目標展開；合規律需要教育教學實踐合于客觀規律；最重要的是要遵循學生成長規律，合必然性體現在“課程思政”和“思政課程”的協同育人[4]。

1.3 數學文化蘊含豐富的思政教育資源

數學課程的思政教育，不是用思政來講思政，而是在當下的專業課知識中向思政上牽引和挖掘，達到潛移默化的效果，“潤思政”細無聲，而不是生搬硬套，強行和思政教育掛鉤。數學文化是人類文化的重要組成部分，它是世界的也是民族的。先輩的數學家們對發展民族數學文化有著重大奉獻，民族數學文化的奮斗史和進步史都可以成為“課程思政”的資源。數學來源于生活，應用于生活，所以數學文化中所蘊含的哲理與人性品質有很多互通之處。如二次函數

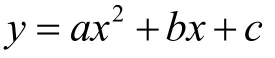
當a＜ 0時，它的曲線是先上升后下降，有最高點，有起有落，很像人生的順境逆境巔峰。如一次函數y=kx+b,(x＞ 0)，b相當于人生的起點，有些人從出生起點就很高（b＞ 0），但是如果后天不努力（k＜ 0），也會越來越差趨近于負無窮；反觀有些人雖然出生起點比較低（b＜ 0），但自己后天加倍努力，積極追求自己的人生理想（k＞ 0），最后必將沖出逆境（x軸），結果越來越好，實現自己的人生價值。數學文化中的黃金分割[5]是一種非常美麗的比例，它常常表現于藝術、建筑以及人體結構。體會這些數學的內涵美，可以讓學生形成一定的審美觀，提高學生的思想品德修養，培養科學的世界觀。

2 教學案例分析——以韓信點兵與中國剩余定理為例

課程內容：數學文化第三章第三節——韓信點兵與中國剩余定理。

2.1 教授內容及挖掘思政元素

2.1.1 以“韓信點兵”的故事引入

向學生講解韓信點兵的故事。韓信是漢高祖劉邦的大將，屢建戰功。有一日韓信數兵，先讓一隊士兵五個人一行，他記下最后一行士兵的人數一人；六個人一行排隊，他記下最后一行人數五個人；七個人一行排隊從閱兵臺前走過，他記下最后一行人數四個人；十一個人一行排隊走過去，最后一行是十個。然后韓信就憑這些數據可以求得這隊士兵的總人數，這里面有什么秘密呢？好像都是做除法時的余數，由此就可以求出士兵的總數嗎[1]？

思政元素：一個中國古代數學的“韓信點兵”的故事作為課程的引入，首先可以帶動學生對這個余數來計算總人數的問題的思考，其次可以讓學生感受到古代中國人民的智慧，從而產生民族自豪感、自信感，激發學生的愛國之情和濃厚的數學興趣。

2.1.2 從另外一個問題（物不知其數問題）著手教學

我們從另一問題介紹這類問題的方法，今有物不知其數，二二數之剩一，三三數之剩二，四四數之剩三，五五數之剩四，六六數之剩五，七七數之剩六，八八數之剩七，九九數之剩八。問物幾何？對于問題的條件，表面上看起來比上一個題還復雜。其實這道題比上題簡單，可以用篩法和公倍數法這兩種方法來解決這一問題。通過舉例，篩法是一般性方法，可以用來解決所有這類問題，但是過程比較繁瑣；公倍數法，將篩法化繁為簡，并通過尋找規律，可以解決具有相同特征的用余數求總數問題[2]151-158。

思政元素：從另一問題入手，化繁為簡，尋找規律的解決問題，可以培養學生辯證地看待問題的思想；篩法和公倍數法的客觀、嚴謹的過程體現了唯物論和辯證法的哲學思想，有助于學生逐步形成辯證唯物主義世界觀。

2.1.3 對“中國剩余定理”進行講授

公元1247 年，南宋數學家秦九韶得到稱為“大衍總數術”的方法，并記錄在《數書九章》中。在歐洲，直到18 世紀，歐拉和拉格朗日等曾對一次同余方程組問題進行研究。高斯在1800 年出版的《算術研究》中，才明確寫出了一次同余方程組的求解定理，并對兩兩互素模的情形給出了嚴格的證明。1852 年，英國傳教士偉烈亞力將《孫子算經》中孫子問題的解法傳到歐洲。1876 年，德國人馬提生指出《孫子算經》中孫子問題的解法以及秦九韶的“大衍總數術”算法與高斯算法是一致的，因此在西方數學史上，一次同余式方程的求解定理常常被稱為“中國剩余定理”（Chinese Remainder Theorem）。此定理用現在的語言表述如下：設d1,d2,…,dn是兩兩互素，x分別被d1,d2,… ,dn除得余數為r1,r2,…,rn，則

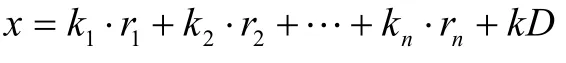
其中D是d1，d2……dn的最小公倍數，ki是d1，d2……,di-1,di+1,……,dn的公倍數且被di除所得余數為1，k為任意整數[2]159-160。

思政元素：中國剩余定理是中國數學家秦九韶最早給出的，這一事實不僅擴大了學生的數學知識面，提升了學生對數學的興趣，也能提高學生的民族自信心和民族自豪感。借助這一名人軼事，向學生講述數學家們對數學真理的發現精神，同時激勵學生以此為榜樣，從而產生對科學知識的善于發現、不斷探索、勇于鉆研的學習精神。

2.1.4 有趣的應用

某單位有100 把鎖，分別編號為1，2，3，……，100。現在要對鑰匙編號，使外單位的人看不懂，而本單位的人一看見鎖的號碼就知道用哪把鑰匙。利用中國剩余定理，把鎖的號碼分別被3、5、7 去除，得到三個余數當做鑰匙的號碼；也可以在得到的每個余數后面加一個常數，為了更加保密，可以每個月更換一次常數[1]160。

思政元素：數學來源于生活，也回歸于生活。善于數學里所學到的定理應用到實際生活中才成就了數學應有的價值。教師讓學生真正理解數學，體會數學的樂趣，感受數學的意義，從而培養他們學會將理論與實踐相結合的科學方法。

2.2 課堂實施策略

學生是課堂的主體，教師應善于將問題“拋出去”，引導學生主動思考、主動融入。在課堂內容的講解過程中，第一種方式可以是“邊知識邊思政”：教師在將專業知識教授給學生的同時，提出相關人生真理，這樣，學生狀態在線、思路在線，效果顯著。第二種方式是“先知識后思政”：可以先將本堂課的專業知識講完，在課堂的最后進行總結升華，引導學生深入思考。

首先，在講授數學史、數學思想、數學方法、傳授數學知識的同時，注重啟發學生對“思政元素”能動地認知和認同，貼近實際生活向學生進行滲透，引導學生主動、自覺學習。

其次，精選相關人物傳記、影像視頻、時事熱點等資料，將國家形勢、國家的大政方針、愛國情懷、工匠精神等巧妙融入到教學過程中，引導學生認識世界與中國發展的大勢，明確歷史使命與時代責任。

再次，從數學思想、數學方法、數學知識與社會實踐結合中去詮釋思政元素，從實際和實踐出發來解釋理論的形成，因事而化、與時俱進。

最后，在教學實施過程中，通過擺事實、講道理直接對學生進行道德教育，同時還要通過潤物細無聲的方式寓道德教育于課程之中。

2.3 課堂總結

課堂包括課上和課下。為提高課程思政的效果，課上教師應善于利用多媒體技術，將政治微視頻植入教學；課下布置思考作業，給學生足夠的查閱相關數學資料的時間，或者留一個相關的政治小作業，讓學生總結這一課的思想收獲和人生感想。