隨機森林算法中數據切分方法研究

路佳佳

（山西工商學院 計算機信息工程學院，山西 太原 030006）

隨機森林是一種可以處理分類問題和回歸問題的算法，該算法一般采用bootstrap sampling 方法進行抽樣，但是在抽樣中存在“包外估計”。為了減少包外估計的誤差，本文考慮對樣本進行合理的數據切分[1]來有效提高模型的性能，減少誤差。本文應用簡單隨機抽樣的方法將大小為n的數據集分成不相交的兩份，并且進行相同的抽樣P次，得到2P份大小為的數據集。然后從中選擇一份建立隨機森林，其中的個樣本作為訓練集，另外的個樣本作為驗證集，通過誤差來分析[2-4]驗證切分方法的有效性。

1 改進的隨機森林算法及其計算步驟

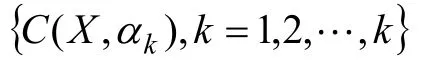
隨機森林是含有多個決策樹的集成分類器[5]，其中｛αk｝是獨立同分布的隨機向量，k表示隨機森林中決策樹的個數。改進的隨機森林算法主要是從數據切分的角度來改進隨機森林。本文研究的改進的隨機森林方法應用于回歸任務和分類任務中。

隨機森林回歸的方法一般針對連續型隨機變量，也就是研究輸出變量y和輸入變量X之間的關系建立數學模型。隨機森林中的參數一般有兩個，一個是樹的棵目數Ntree，另一個是隨機特征數Mtry。即

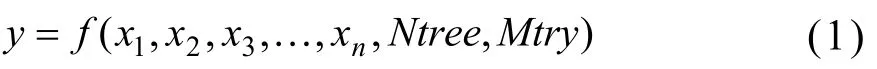
隨機森林分類的方法一般針對離散型隨機變量[3]，假設輸入變量X，通過樹的分類結果進行投票，將多數的投票結果作為最終的預測結果，即

其中L(x)為聯合分類的結果，Pi(x)為第i個分類樹的結果。

改進的隨機森林算法預測步驟包括以下三步。

（1）產生數據集。

（2）應用簡單隨機抽樣的方法對數據集進行切分，抽取的一半數據記為D1，剩余的另一半數據記為D2，D1與D2互不相交。進行相同的抽取P次，將數據集切分成2P份。

（3）切分之后選取的數據中一半作為訓練集，另一半作為驗證集建立隨機森林模型。將數據集中的輸入變量X輸入到使用訓練集得到的模型中，在回歸任務中采用簡單平均法計算出的平均值作為預測值。在分類任務中采用投票法將分類結果中出現次數最多的結果作為最終分類結果。

在具體實驗過程中借助R 統計軟件中的包random forest 庫函數實現上述步驟。

2 實驗分析

模擬出n=1 000,p=150（數據個數為1 000，維數為150）的多元正態數據集，x為150 維，y為標準正態分布下的隨機數，然后對模擬的數據集進行3 次切分，其中250 個樣本作為訓練集，另外的250 個樣本作為驗證集，設置隨機森林中樹的棵目數ntree的值，從2 到500 變化。通過UCI數據集下載的iris 數據集作為真實數據。該數據集包含150 個樣本，每個數據包含四個特征和對應的樣本類別信息。

2.1 模擬數據處理結果

均方根誤差從一定程度上可以描述偏差，設obi(i=1,2,…,n)表示觀測值，用ti表示預測值，則均方根誤差的計算公式為

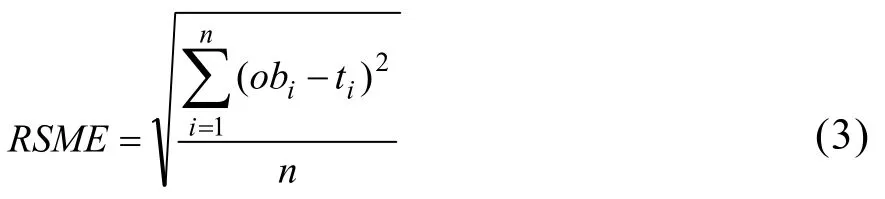
隨機切分情況下模擬實驗的結果如圖1 所示。

從圖1 可以看出隨著樹的棵目數的增加，均方根誤差rsme逐漸減少，當樹的棵數在100 左右時，隨機森林的rsme幾乎穩定在0.96。圖2 是切分情況下計算的偏差和樹的棵數的散點圖，可以看出當樹的棵數在100 時，偏差穩定在10 左右。

圖3 是不進行隨機切分的情況下，模擬實驗結果。從圖中可以看出，隨著樹的棵數的增加，均方根誤差rsme逐漸減少，當增加到一定程度時rsme穩定在1.00。表明對數據進行隨機切分對隨機森林的偏差有一定程度的影響，可以減少偏差，并且當樹的棵數在100 左右和500 時可以達到幾乎相同的偏差。

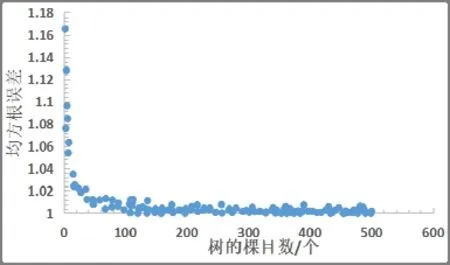
圖3 不切分時ntree 與rsme 關系圖

對于分類問題，模擬數據集x為150 維，y為0 或1 的二分類任務，不進行隨機切分的情況下，樹的棵目數（ntree）與分類準確率（accuracy）的關系圖如圖4 所示，進行隨機切分的數據處理結果如圖5 所示。從圖4 可以看出，不進行切分的隨機森林的準確率隨著樹的棵目數的增大穩定在0.85。從圖5 可以看到，隨著樹的棵目數的增加，分類的準確率在逐漸增大，當樹的棵目數增大到100 時，分類的準確率逐漸穩定在0.9。

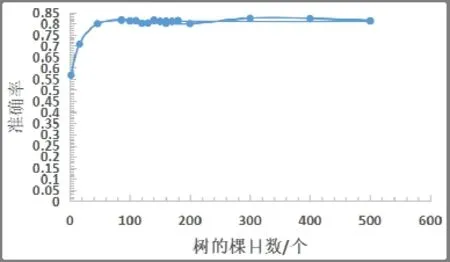
圖4 不進行切分ntree 與accuracy 關系圖

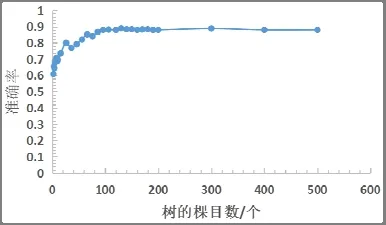
圖5 進行切分ntree 與accuracy 關系圖

用隨機切分的隨機森林做100 次實驗，平均誤差率，典型結果見圖7。從圖中可見，平均誤差率為4.974 2%；用沒有隨機切分的隨機森林做100次實驗，典型結果見圖8。從圖中可知，平均誤差率為6.595 2%。

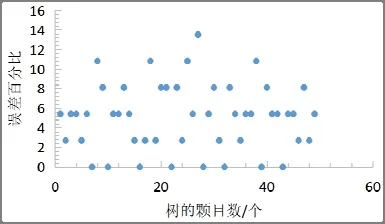
圖7 切分處理情況下的誤差率

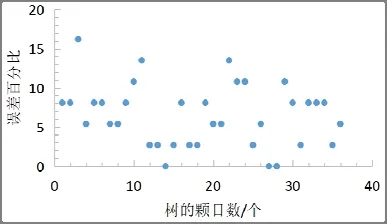
圖8 不進行切分情況下的誤差率

2.2 iris 數據集數據處理結果

繪制不經切分處理的隨機森林和經切分處理的隨機森林情況下的均方差圖，見圖9 和圖10。從兩個圖中可以看出，經過切分的均方差圖誤差較為穩定，誤差值也較小。

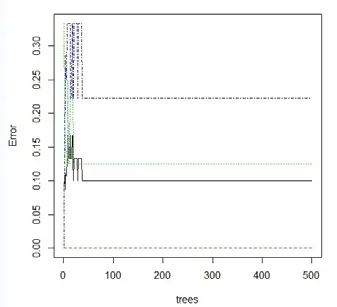
圖9 不進行切分情況下的均方差

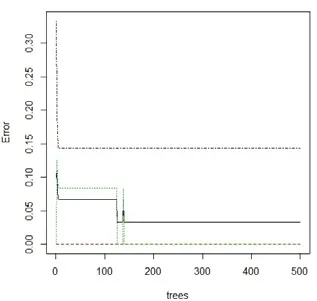
圖10 進行切分情況下的均方差

3 結論

應用隨機切分數據集的方法對分類任務的準確率的提高和回歸任務的偏差都有一定的提高。方法應用與iris 數據集表現出較高的穩定性。