例談如何在數(shù)學(xué)化的過(guò)程中滲透數(shù)學(xué)建模
——以“三角函數(shù)的概念”教學(xué)為例

李 平

（韶關(guān)市第一中學(xué)，廣東 韶關(guān) 512005）

學(xué)習(xí)了章建躍、張艷嬌和金克勤3位老師撰寫(xiě)的《數(shù)學(xué)建模活動(dòng)的課程理解、教材設(shè)計(jì)與教學(xué)實(shí)施》一文，對(duì)新教材中關(guān)于數(shù)學(xué)建模活動(dòng)的編寫(xiě)思路，數(shù)學(xué)建模活動(dòng)的教材結(jié)構(gòu)有了新的認(rèn)識(shí).文章中提出“要在數(shù)學(xué)化的過(guò)程中滲透數(shù)學(xué)建模”［1］，本文在結(jié)合新課程標(biāo)準(zhǔn)和研究?jī)?nèi)容解析的基礎(chǔ)上給出了“三角函數(shù)的概念”一節(jié)的教學(xué)設(shè)計(jì)，并對(duì)教學(xué)設(shè)計(jì)的實(shí)施進(jìn)行了反思.

1 內(nèi)容解析

1.1 課標(biāo)要求

《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)》（2017年版）中“內(nèi)容要求”對(duì)三角函數(shù)概念的教學(xué)要求是：借助單位圓理解三角函數(shù)（正弦、余弦、正切）的定義［2］.并給出了教學(xué)應(yīng)達(dá)到的目標(biāo)及建議采取的教學(xué)手段，即從學(xué)生已知的、基于變量關(guān)系的函數(shù)定義入手，引導(dǎo)學(xué)生通過(guò)生活或數(shù)學(xué)中的問(wèn)題，構(gòu)建函數(shù)的一般概念，體會(huì)用對(duì)應(yīng)關(guān)系定義函數(shù)的必要性.

1.2 教材分析

本文探討的是人教A版高中數(shù)學(xué)必修第一冊(cè)（2019）第五章第二節(jié)的內(nèi)容［3］，主要內(nèi)容是三角函數(shù)的概念.三角函數(shù)是描述周期運(yùn)動(dòng)現(xiàn)象的重要的數(shù)學(xué)模型，有非常廣泛的應(yīng)用.三角函數(shù)的定義是本章最基本的概念，對(duì)三角內(nèi)容的整體學(xué)習(xí)至關(guān)重要，是其他所有知識(shí)的出發(fā)點(diǎn).緊緊扣住三角函數(shù)定義這個(gè)寶貴的源泉，可以自然地導(dǎo)出本章的具體內(nèi)容：定義域、符號(hào)判斷、值域、同角三角函數(shù)關(guān)系、多組誘導(dǎo)公式、多組變換公式、圖像和性質(zhì).三角函數(shù)的定義在教材中起著承前啟后的作用，一方面，通過(guò)這部分內(nèi)容的學(xué)習(xí)，可以幫助學(xué)生更加深入理解函數(shù)這一基本概念，另一方面它又為平面向量、解析幾何等內(nèi)容的學(xué)習(xí)作必要的準(zhǔn)備.三角函數(shù)知識(shí)還是物理學(xué)、高等數(shù)學(xué)、測(cè)量學(xué)、天文學(xué)的重要基礎(chǔ).

三角函數(shù)定義的學(xué)習(xí)是學(xué)好全章內(nèi)容的關(guān)鍵，如果學(xué)生掌握不好，將直接影響到后續(xù)內(nèi)容的學(xué)習(xí)，由三角函數(shù)定義的基礎(chǔ)性和應(yīng)用的廣泛性決定了其重要性.

1.3 核心素養(yǎng)及蘊(yùn)含的數(shù)學(xué)思想方法

數(shù)學(xué)抽象.三角函數(shù)主要結(jié)合單位圓圖形是從單位圓中心角弧度數(shù)與中心角的終邊和單位圓交點(diǎn)的橫坐標(biāo)、縱坐標(biāo)及縱坐標(biāo)與橫坐標(biāo)的比值的對(duì)應(yīng)關(guān)系中抽象出三角函數(shù)的概念，體現(xiàn)了數(shù)學(xué)抽象和數(shù)形結(jié)合的思想和方法.

邏輯推理.三角函數(shù)從研究特殊角與單位圓交點(diǎn)的坐標(biāo)出發(fā)，通過(guò)歸納、類比發(fā)現(xiàn)相應(yīng)的對(duì)應(yīng)關(guān)系.體現(xiàn)了特殊到一般的思想方法.

數(shù)學(xué)建模.三角函數(shù)一課在書(shū)本一開(kāi)始就明確了任務(wù)：?jiǎn)挝粓A圓O上的點(diǎn)P以A為起點(diǎn)做逆時(shí)針?lè)较蛐D(zhuǎn)，建立一個(gè)數(shù)學(xué)模型，刻畫(huà)點(diǎn)P的位置變化情況.并提供了研究的路徑：明確研究對(duì)象→對(duì)應(yīng)關(guān)系的特點(diǎn)分析→定義.

直觀想象.借助單位圓及直角坐標(biāo)系觀察點(diǎn)P的位置變化特點(diǎn)及運(yùn)動(dòng)規(guī)律，建立了形與數(shù)的聯(lián)系，構(gòu)建課堂要研究問(wèn)題的直觀模型，體現(xiàn)了數(shù)形結(jié)合的思想方法.

1.4 教學(xué)目標(biāo)

（1）初步理解借助單位圓上點(diǎn)的坐標(biāo)定義三角函數(shù)，理解任意角的三角函數(shù)的概念；

（2）在三角函數(shù)定義的過(guò)程中進(jìn)一步認(rèn)知函數(shù)的本質(zhì)，體會(huì)數(shù)形結(jié)合思想方法的作用；

（3）經(jīng)歷三角函數(shù)概念的抽象過(guò)程，提升學(xué)生思維的嚴(yán)謹(jǐn)性，發(fā)展數(shù)學(xué)抽象素養(yǎng).

1.5 教學(xué)重點(diǎn)與難點(diǎn)

教學(xué)重點(diǎn)是任意角的三角函數(shù)概念，其難點(diǎn)在于用單位圓上點(diǎn)的坐標(biāo)定義三角函數(shù).

2 教學(xué)設(shè)計(jì)

2.1 創(chuàng)設(shè)情景，導(dǎo)入新課

問(wèn)題引入：在客觀世界中存在大量循環(huán)往復(fù)、周而復(fù)始的周期現(xiàn)象，比如日出日落、鐘擺運(yùn)動(dòng)等，勻速圓周運(yùn)動(dòng)是這類現(xiàn)象的代表，函數(shù)是描述客觀世界變化規(guī)律的重要數(shù)學(xué)模型，那么勻速圓周運(yùn)動(dòng)的運(yùn)動(dòng)規(guī)律該用什么函數(shù)模型刻畫(huà)呢？

如圖1所示，圓O上的點(diǎn)P以A為起點(diǎn)做逆時(shí)針旋轉(zhuǎn)，在把角的范圍推廣到任意角后，可以借助角α的大小變化刻畫(huà)點(diǎn)P的位置變化.根據(jù)弧度制的定義，角α的大小與圓O的半徑無(wú)關(guān)，能否建立一個(gè)函數(shù)模型，刻畫(huà)點(diǎn)P的位置變化情況?

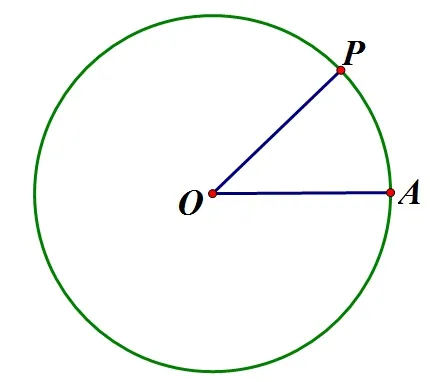
圖1 點(diǎn)P的位置變化圖

設(shè)計(jì)意圖：開(kāi)門見(jiàn)山引出研究?jī)?nèi)容、過(guò)程與研究方法，指明點(diǎn)P隨著角度的變化而變化，明確構(gòu)建函數(shù)模型的目標(biāo)，讓學(xué)生初步了解本節(jié)課學(xué)習(xí)的方向，為具體研究指明方向.

2.2 引導(dǎo)探究，形成新知

分析要解決這個(gè)問(wèn)題需要什么工具？

首先，要建立函數(shù)模型，要利用直角坐標(biāo)系.

其次，根據(jù)任意角的定義，需要借助單位圓.

如圖2所示，以單位圓的圓心O為坐標(biāo)原點(diǎn)，以射線OA為x軸的非負(fù)半軸，建立直角坐標(biāo)系，點(diǎn)A的坐標(biāo)是（1，0），點(diǎn)P的坐標(biāo)是（x，y）.把該問(wèn)題抽象為一個(gè)點(diǎn)P從點(diǎn)A（1，0）開(kāi)始在單位圓上的運(yùn)動(dòng).

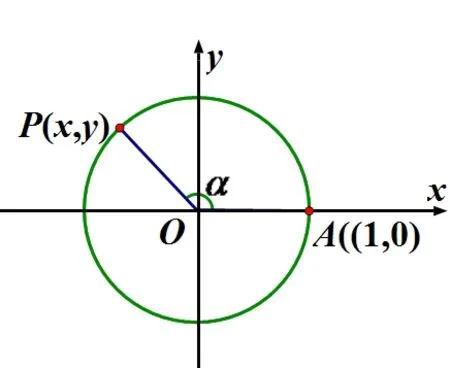
圖2 點(diǎn)P在單位圓上的 運(yùn)動(dòng)

問(wèn)題1：這個(gè)運(yùn)動(dòng)過(guò)程中的有哪些變量，判斷它們之間是否具有函數(shù)關(guān)系.如果有，能否寫(xiě)出函數(shù)解析式？

（1）點(diǎn)P在單位圓上運(yùn)動(dòng)過(guò)程中涉及的變量有：點(diǎn)P的橫坐標(biāo)x、縱坐標(biāo)y，弧長(zhǎng)l，旋轉(zhuǎn)角度α；

（2）判斷變量：x，y，l，α間的哪兩個(gè)變量能否構(gòu)成函數(shù)關(guān)系？

過(guò)點(diǎn)P作PM⊥x軸于M，根據(jù)勾股定理可知OM2+PM2=1，即x2+y2=1，顯然變量x、y間的對(duì)應(yīng)關(guān)系不符合函數(shù)定義.在弧度制學(xué)習(xí)中已經(jīng)知道變量l，α之間的關(guān)系，并且變量x，y與α的關(guān)系和x，y與l的關(guān)系等價(jià)，所以只需研究變量x，y與α的關(guān)系.

問(wèn)題2：若角α終邊與單位圓交于點(diǎn)P，如何求點(diǎn)P的坐標(biāo)？

追問(wèn)1：當(dāng)遇到一般性問(wèn)題應(yīng)該如何研究？

追問(wèn)3：任意給定一個(gè)角α，點(diǎn)P的坐標(biāo)唯一確定嗎？

因?yàn)閱挝粓A的半徑不變，點(diǎn)P的坐標(biāo)只與角α的大小有關(guān)，當(dāng)角α確定時(shí)，點(diǎn)P的坐標(biāo)是（x，y）也唯一確定.

追問(wèn)4：在展示的運(yùn)動(dòng)變化的過(guò)程中，觀察角α的終邊與單位圓的交點(diǎn)P的坐標(biāo)，有什么發(fā)現(xiàn)？能否運(yùn)用函數(shù)的語(yǔ)言刻畫(huà)這種對(duì)應(yīng)關(guān)系呢？

對(duì)任意一個(gè)實(shí)數(shù)α，它的終邊OP與單位圓的交點(diǎn)P的橫、縱坐標(biāo)x、y都是唯一確定的，有如下對(duì)應(yīng)關(guān)系：任意角α（弧度）→唯一實(shí)數(shù)x；任意角α（弧度）→唯一實(shí)數(shù)y．

一般地，任意給定一個(gè)角α∈R，它的終邊OP與單位圓交點(diǎn)P的坐標(biāo)，無(wú)論是橫坐標(biāo)x，還是縱坐標(biāo)y，都是唯一確定的.所以，點(diǎn)P的橫坐標(biāo)x、縱坐標(biāo)y都是角α的函數(shù).

設(shè)計(jì)意圖：以函數(shù)的對(duì)應(yīng)關(guān)系為指向，使學(xué)生確認(rèn)相應(yīng)的對(duì)應(yīng)關(guān)系滿足函數(shù)的定義，角的終邊與單位圓的交點(diǎn)的橫、縱坐標(biāo)都是圓心角α（弧度）的函數(shù)，為引出三角函數(shù)的定義做好鋪墊.

接著給出這些函數(shù)的定義：如圖3所示，設(shè)α是一個(gè)任意角，α∈R，它的終邊OP與單位圓相交于點(diǎn)P（x，y），那么把點(diǎn)P的縱坐標(biāo)y叫做α的正弦函數(shù)，記做sinα，即y=sinα； 把點(diǎn)P的橫坐標(biāo)x叫做α的余弦函數(shù)，記做cosα，即x=cosα； 把點(diǎn)P的縱坐標(biāo)與橫坐標(biāo)的比值叫做α的正切函數(shù)，記做tanα，即=tanα（x≠0）.

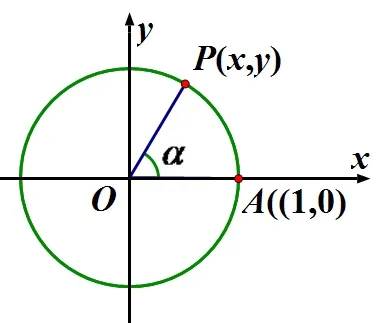
圖3 三角函數(shù)定義輔助圖

問(wèn)題3：正弦函數(shù)、余弦函數(shù)、正切函數(shù)的對(duì)應(yīng)關(guān)系各是什么？

實(shí)數(shù)α（弧度）對(duì)應(yīng)于點(diǎn)P的縱坐標(biāo)y→正弦函數(shù)；

實(shí)數(shù)α（弧度）對(duì)應(yīng)于點(diǎn)P的橫坐標(biāo)x→余弦函數(shù)；

當(dāng)點(diǎn)P的橫坐標(biāo)為0時(shí)，角α的終邊在y軸上，此時(shí)，所以=tanα無(wú)意義.

因此，對(duì)于確定的角α，的值也是唯一確定的，所以=tanα（x≠0）也是以角為自變量，以單位圓上點(diǎn)的縱坐標(biāo)與橫坐標(biāo)的比值為函數(shù)，稱為正切函數(shù).實(shí)數(shù)α（弧度）對(duì)應(yīng)于點(diǎn)P的縱坐標(biāo)y與橫坐標(biāo)x（x≠0）之比→正切函數(shù).

追問(wèn)1：任意角三角函數(shù)的定義是否符合高中函數(shù)的定義呢？

正弦、余弦、正切都是以角為自變量，以單位圓上點(diǎn)的坐標(biāo)或者坐標(biāo)的比值為函數(shù)值的函數(shù).由于角的集合與實(shí)數(shù)集之間可以建立一一對(duì)應(yīng)關(guān)系， 所以三角函數(shù)可以看成是自變量為實(shí)數(shù)的函數(shù).

按照函數(shù)的定義與常用的符號(hào)，通常將它們記為：正弦函數(shù)y=sinx；余弦函數(shù)y=cosx；正切函數(shù)y=tanx.將正弦函數(shù)、余弦函數(shù)和正切函數(shù)統(tǒng)稱為三角函數(shù).

追問(wèn)2：任意角三角函數(shù)的定義域分別是什么呢?

很明顯，正弦函數(shù)和余弦函數(shù)的定義域都是實(shí)數(shù)集，即x∈R，對(duì)于正切函數(shù)而言，要求點(diǎn)P的橫坐標(biāo)x≠0，即角α的終邊OP不能位于y軸上，那么正切函數(shù)的定義域?yàn)?/p>

追問(wèn)3：這個(gè)定義相對(duì)于銳角三角函數(shù)的定義有什么不同呢?

任意角的三角函數(shù)是通過(guò)角與單位圓交點(diǎn)的坐標(biāo)定義的，銳角三角函數(shù)是通過(guò)直角三角形邊長(zhǎng)的比值定義的，在單位圓中直角三角形斜邊為1，所以銳角三角函數(shù)也可用角的終邊與單位圓交點(diǎn)的坐標(biāo)定義，此時(shí)終邊上的點(diǎn)都在第一象限，因此銳角三角函數(shù)值都是正數(shù)，而任意角的三角函數(shù)值可以是負(fù)數(shù).

追問(wèn)4：“任意角的三角函數(shù)”與“銳角三角函數(shù)”這兩個(gè)概念有什么異同?

設(shè)計(jì)意圖：引導(dǎo)學(xué)生將任意角三角函數(shù)納入到函數(shù)中，豐富學(xué)生對(duì)三角函數(shù)的認(rèn)知，另外，注意任意角為軸線角的特殊情況，讓學(xué)生更全面地認(rèn)識(shí)任意角的三角函數(shù)，體現(xiàn)數(shù)學(xué)的嚴(yán)謹(jǐn)性.

2.3 理解概念，運(yùn)用新知

例1求的正弦、余弦和正切值.

解如圖4所示，在直角坐標(biāo)系中，作，此時(shí)∠AOB的終邊與單位圓的交點(diǎn)B的坐標(biāo)為，所以

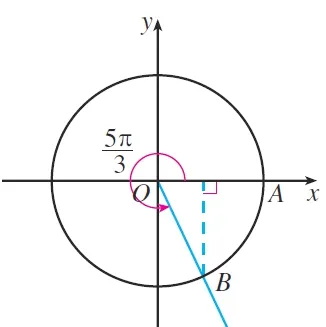
圖4 例1輔助圖

設(shè)計(jì)意圖：通過(guò)概念的簡(jiǎn)單應(yīng)用，明確用定義求三角函數(shù)值的基本步驟，進(jìn)一步理解定義的內(nèi)涵.

例2如圖5所示，設(shè)α是一個(gè)任意角，它的終邊上任意一點(diǎn)P（不與原點(diǎn)O重合）的坐標(biāo)為（x，y），點(diǎn)P與原點(diǎn)的距離為r.

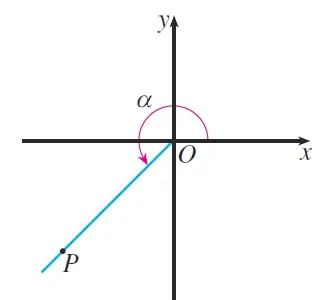
圖5 例2輔助圖

引導(dǎo)學(xué)生分析問(wèn)題：

你能根據(jù)三角函數(shù)的定義作圖表示sinα和cosα嗎？

解設(shè)角α的終邊與單位圓交于點(diǎn)P0（x0，y0），分別過(guò)點(diǎn)P，P0作x軸的垂線PM，P0M0，垂足分別為M，M0，如圖6所示，則|PM|=|y|，|P0M0|=|y0|，|OM|=|x|，|OM0|=|x0|，△OMP≌△OM1P1.

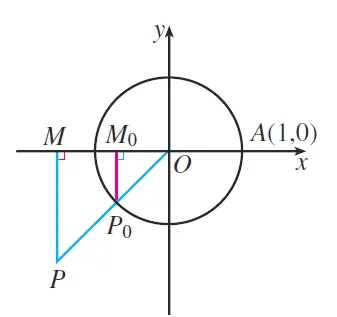
圖6 例2解題輔助圖

設(shè)計(jì)意圖：通過(guò)問(wèn)題引導(dǎo)，使學(xué)生找到△OMP、OM1P1，并利用它們的相似關(guān)系，根據(jù)三角函數(shù)的定義得到證明.

追問(wèn)：例2實(shí)際上給出了任意角的三角函數(shù)的另外一種定義，而且這種定義與已有的定義是等價(jià)的，能否用嚴(yán)格的數(shù)學(xué)語(yǔ)言敘述這個(gè)定義嗎？

一般地，對(duì)于任意角α，角α終邊上的任意一點(diǎn)P的坐標(biāo)為（x，y），它到原點(diǎn)O的距離為那么

顯然任意角α的三角函數(shù)值不會(huì)隨點(diǎn)的位置的變化而變化.

2.4 應(yīng)用新知，總結(jié)提升

任意角三角函數(shù)的概念是三角函數(shù)知識(shí)的基礎(chǔ)，以后要學(xué)習(xí)的有關(guān)三角函數(shù)其他知識(shí)都建立在對(duì)三角函數(shù)的概念的理解與認(rèn)識(shí)上，所以同學(xué)們一定要認(rèn)真學(xué)習(xí)和體會(huì)所學(xué)的知識(shí).

三角函數(shù)是如何定義的？除了學(xué)習(xí)單位圓定義，還有什么定義方法？

（1）單位圓定義法：建立直角坐標(biāo)系，使角α的頂點(diǎn)與坐標(biāo)原點(diǎn)重合，終邊與單位圓的交點(diǎn)為P，即可由點(diǎn)P坐標(biāo)（x，y）得到三角函數(shù)定義.

正弦函數(shù)：y=sinx（x∈R）；余弦函數(shù)：y=cosx（x∈R）；正切函數(shù)：

（2）終邊定義法：建立直角坐標(biāo)系，對(duì)于任意角α，角α終邊上的任意一點(diǎn)P的坐標(biāo)為（x，y），它到原點(diǎn)O的距離為，那么

在研究三角函數(shù)概念的過(guò)程中，你體會(huì)到了什么數(shù)學(xué)思想方法？

在任意角的三角函數(shù)的概念建構(gòu)的過(guò)程中，運(yùn)用了轉(zhuǎn)化與化歸、數(shù)形結(jié)合、函數(shù)思想，這些思想方法在今后的學(xué)習(xí)中非常重要，一定要認(rèn)真體會(huì).

3 總結(jié)反思

對(duì)傳統(tǒng)的概念授課教師比較注重知識(shí)性教學(xué)，經(jīng)常將理論教學(xué)與實(shí)踐教學(xué)分離，而利用數(shù)學(xué)建模的教學(xué)過(guò)程啟發(fā)、引導(dǎo)學(xué)生經(jīng)歷建模的全過(guò)程，并讓學(xué)生有實(shí)質(zhì)性的思考，可以更加深刻地理解三角函數(shù)的定義形成的過(guò)程.正如章建躍老師所說(shuō)：“加強(qiáng)數(shù)學(xué)與現(xiàn)實(shí)的聯(lián)系是課改的一個(gè)基本理念，也是數(shù)學(xué)教材改革的一個(gè)基本方向”［1］.作為一線教師更應(yīng)該注重轉(zhuǎn)變教學(xué)方式、更新教學(xué)觀念更好更快的適應(yīng)課改要求，將學(xué)生核心素養(yǎng)的培養(yǎng)在課堂教學(xué)中落到實(shí)處.