足尺鋼框架結構中樓板火災行為數值分析

王 勇，郭文軒，李凌志,2，簡曉紅，馬 帥，張耕源，趙行行

(1. 中國礦業大學/中國礦業大學(北京) 深部巖土力學與地下工程國家重點實驗室，江蘇，徐州 221008；2. 同濟大學土木工程學院，上海 200092；3. 浙江瑞邦科特檢測有限公司，浙江，杭州 310000；4. 中國建筑科學研究院有限公司，北京 100013)

目前，國內外學者對混凝土雙向板火災行為進行了大量試驗和數值分析，取得了較多的研究成果[1?7]。值得指出的是，上述研究多針對簡支板或連續板火災行為方面[8?10]，對結構中混凝土雙向板火災行為數值方面相對較少。事實上，由于受火構件和相鄰未升溫結構單元的相互作用，結構中樓板火災行為與單一板構件火災行為不同，為了準確理解和掌握樓板及構件在結構中火災行為，有必要對其力學機理進行深入分析。

近年來，國內外學者進行了一系列整體結構火災試驗。例如，1995年?1996年，英國Cardington的BRE火災研究實驗室對一足尺多層組合結構進行6次大型火災試驗[11]，研究表明，由于梁柱約束作用，火災下樓板大變形階段出現受拉薄膜效應，其有助于提高結構抗火性能。然而，上述研究主要側重于火災下壓型鋼板組合樓板力學行為，其相關研究結果無法完全用于指導鋼筋混凝土樓板抗火設計。因此，2013年?2015年，董毓利課題組[12?14]對一足尺3層鋼框架結構中樓板進行4次大型火災試驗，具體為頂層中區格和角區格兩次火災試驗(鋼梁未受火)、第二層四區格火災試驗(內部鋼梁受火)和一層六區格火災試驗(內部鋼梁受火)，研究表明受火跨位置、數量及鋼梁是否受火對結構中樓板變形、裂縫和破壞模式等有重要影響。然而，安全起見，上述試驗鋼柱均未直接受火。Nguyen和Tan[15?17]開展了結構中組合板(縮尺)抗火性能試驗，重點研究了(無)防火保護次梁和邊界轉動約束對火災下組合樓板變形和破壞模式等影響規律。研究表明：次梁能夠降低組合樓板跨中變形和提高其承載力(受拉薄膜效應)，轉動約束易導致板角壓碎和邊梁出現較寬裂縫；當樓板跨中位移達到板厚時，開始出現受拉薄膜效應。然而，上述試驗板均為縮尺板，致使組合板截面溫度分布與實際結構不符。總之，上述結構或構件火災試驗復雜、周期長和費用高，進而在試驗基礎上，有必要對火災下樓板溫度、變形、薄膜機理和各構件內力發展規律開展深入數值分析。

目前，國內外學者對火災下簡支雙向(組合)板溫度、變形和薄膜機理等進行數值分析，指出火災下簡支雙向(組合)板受拉薄膜效應有利于提高其耐火性能[18]。然而，上述研究主要針對簡支雙向(組合)板，未考慮不同邊界條件對其薄膜機理影響，即忽略結構連續性和結構中其他構件約束作用。因此，王勇等[19]對火災下單(雙)向面內約束雙向板力學性能開展數值分析，研究表明約束力水平、約束方向、配筋率和長寬比等對雙向板裂縫間距、裂縫樣式和板底爆裂等破壞模式有重要影響。此外，文獻[10]研究了受火跨數量、位置、受火跨順序、蔓延間隔時間、板厚和配筋率等對火災下三跨連續雙向板溫度、變形、裂縫和破壞樣式等影響規律。上述數值研究主要側重于板構件，未考慮梁柱約束作用。實際上，Huang等[20]發展Vulcan軟件，對火災下足尺組合結構中樓板變形和薄膜機理等結構行為進行數值分析，重點研究了幾何(非)線性對火災下組合樓板變形行為和薄膜機理的影響規律，并指出單(雙)向曲率變形對薄膜拉力產生及樓板抗火性能的影響規律。Ellobody和Bailey[21]采用ABAQUS軟件，研究了不同火災蔓延工況(不同火災區域和火災蔓延時間間隔)對結構中后張拉混凝土樓板變形行為的影響規律，研究表明樓板最大變形可能發生在火災蔓延工況或多房間同時受火工況，結構設計時應考慮火災蔓延工況。然而，不同火災工況下樓板薄膜機理和梁柱構件內力發展規律并未給出。Nguyen和Tan等[15?16]采用ABAQUS軟件，結合熱彈塑性損傷本構和S4R殼單元，對結構中組合樓板溫度、變形和梁板主應力分布等進行數值分析，數值表明次梁對組合樓板內鋼筋應力分布和幅值及最終破壞模式(鋼筋斷裂位置)有重要影響，即跨中鋼筋斷裂(無次梁時)和邊梁附近鋼筋斷裂(有次梁時)。Gernay和Khorasani[22]采用SAFIR軟件，結合結構性能化抗火設計目標，對不同火災工況下(單個房間受火、火災蔓延和鋼柱倒塌后受火)鋼框架結構中組合樓板變形、薄膜機理、鋼梁軸力和彎矩等進行分析；研究表明在性能化抗火設計時，應充分發揮受拉薄膜效應對提高結構抗火性能的有利作用，特別是鋼柱破壞后的結構整體穩定性方面。然而，上述研究主要側重于火災下組合(預應力)樓板力學行為，所得結論能否用于指導鋼筋混凝土樓板抗火設計還有待于深入研究。同時，有必要研究受火板格位置和數量以及鋼梁是否受火對結構中各(未)受火板格薄膜效應發展及分布規律。

基于上述研究，本文采用Vulcan程序，對董毓利課題組[12?13]頂層和第二層樓板火災試驗進行數值分析；研究混凝土膨脹應變對火災下結構中構件變形的影響規律；分析受火跨數量和位置對結構中樓板裂縫、薄膜機理和彎矩分布等影響規律；研究結構中鋼梁和鋼柱的內力發展趨勢。本研究有助于理解火災下結構構件間相互作用、傳力路徑及內力重分布行為，為結構性能化抗火設計提供數值參考。

1 試驗板簡述

1.1 試件板

文獻[12 ? 13]對一足尺3層鋼框架結構中的頂層(中區格和角區格)和第2層樓板(2×2區格)進行火災試驗研究，試驗樓為典型鋼框架結構，由樓板、鋼梁、鋼柱以及填充墻組成，如圖1(a)所示。如圖1(b)所示，每層均為3×3跨，每跨為4500 mm×4500 mm，圖中給出每個板格(A～I)、鋼梁名稱(L1～L12)和鋼柱名稱(如A1～A4)。

對于頂層，分別開展兩次試驗，即角區格(A)和中區格(E)，所有鋼梁均未受火[12]；對于第二層樓板，受火區格為A、B、D和E四個區格，內部四個鋼梁受火[13]。為便于表述，分別定義為試驗I、II和III。所有試驗柱和節點均未直接受火。

1.2 試驗方案

對于試驗I、II和III，均為自行設計火災試驗爐，試驗爐外圍鋼梁、所有鋼柱及梁柱節點均不受火；對于試驗III，爐內4個鋼梁均受火。試驗前，樓板放置砂袋模擬2.0 kPa活荷載。

對于每試驗，沿爐墻均勻布置若干K型熱電偶測量爐溫，數值分析時采用爐溫平均值；沿板厚布置K型熱電偶，用于測量混凝土及鋼筋溫度。采用差動式位移傳感器測量變形。所有數據采用安捷倫數據儀進行采集，采集時間間隔15 s。

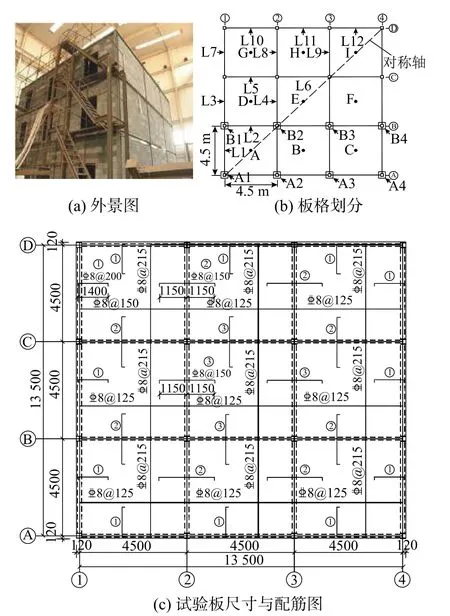
圖 1 鋼框架結構Fig.1 Steel-framed building

1.3 試驗結果

1)平均爐溫-時間曲線

三試驗平均爐溫-時間曲線如圖2所示。可知，三爐溫曲線均低于ISO834標準升溫曲線，試驗I、II和III停火時間分別為270 min、300 min和290 min，且平均最大爐溫分別為881 ℃、890 ℃和787 ℃。

2)構件溫度-時間曲線

圖3為距板底(0 mm)不同位置處混凝土試驗溫度-時間曲線。可知，對于試驗I、II和III，停火時，板底(板頂)最大溫度分別為732.9 ℃(192.6 ℃)、733.7 ℃(231.1 ℃)和670.2 ℃(214.5 ℃)。明顯地，由于較高爐溫，試驗I和II板溫度梯度大于試驗III。

圖4(a)～圖4(c)為試驗I、II和III板底(頂)鋼筋平均溫度-時間試驗關系曲線和計算曲線對比，圖4(d)為試驗III內受火鋼梁L2上翼緣、腹板和下翼緣溫度-時間試驗曲線和計算曲線對比。可知，停火時，試驗I、II和III中板底(頂)鋼筋最大平均溫度分別為632.1 ℃(231.8 ℃)、645.7 ℃(281.8 ℃)和585.3 ℃(179.1 ℃)。此外，停火時，試驗III中鋼梁L2截面平均溫度為698.6 ℃。

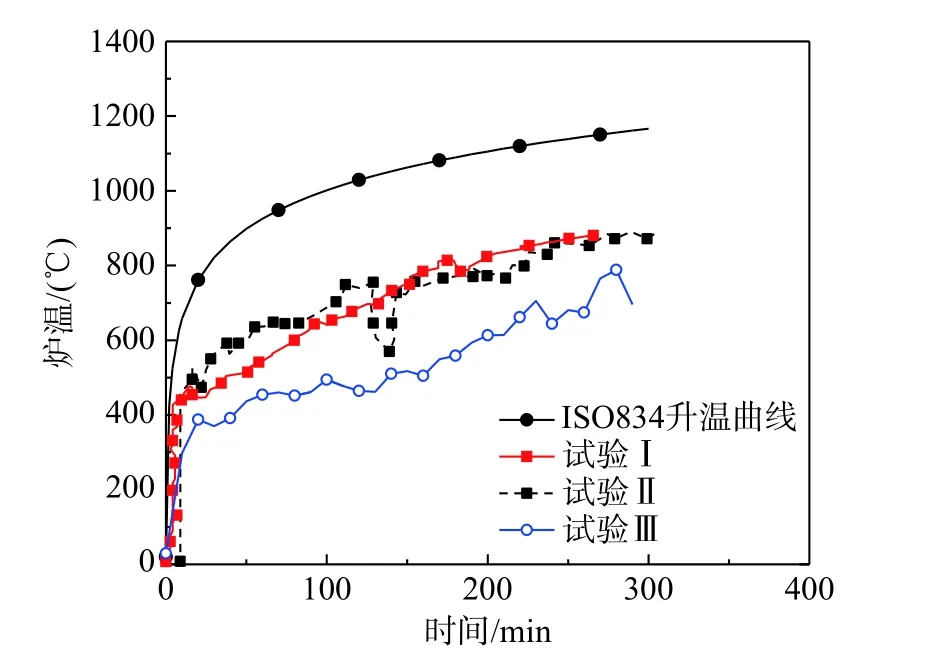
圖 2 三試驗平均爐溫-時間曲線Fig.2 Average furnace temperature-time curves of three tests

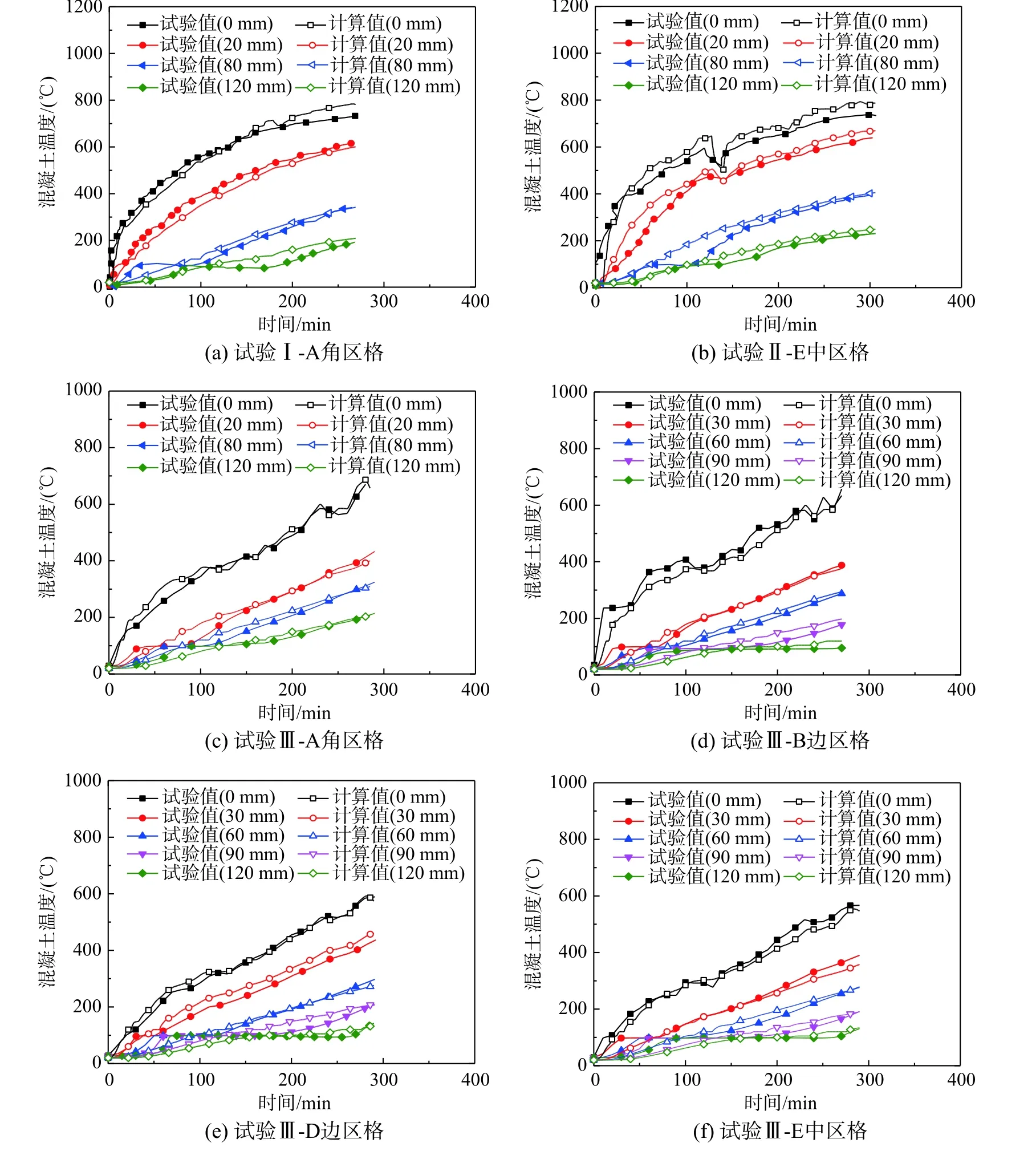
圖 3 試驗板混凝土溫度場計算結果與試驗結果對比Fig.3 Comparison of predicted and tested temperatures of concrete tested slabs

3)跨中撓度-時間曲線

圖5為三試驗中各受火板格跨中撓度(平面外位移)-時間試驗曲線和計算曲線對比。

一方面，對比可知受火位置和數量對樓板變形趨勢有重要影響，如試驗III中，四區格跨中變形出現不同時長的變形平臺，如A區格(50 min～80 min)、B區格(100 min～160 min)、D區格(66 min～155 min)和E區格(35 min～130 min)。而試驗I和II中兩板格跨中變形未出現變形平臺。另一方面，停火時，試驗I和II跨中變形為?137.8 mm和?113.4 mm，而試驗III中A、B、D和E四區格跨中變形分別為?177.7 mm、?110.8 mm、?137.8 mm和?126.9 mm，均未達到變形破壞準則(l/20)。

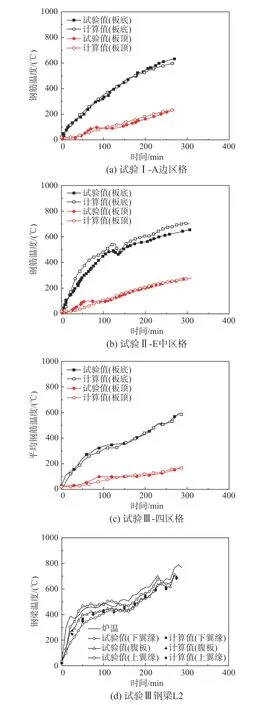
圖 4 試驗板溫度場鋼筋(梁)計算結果與試驗結果對比Fig.4 Comparison of predicted and tested temperatures of concrete tested slabs

此外，圖5(b)計算結果和試驗結果有一定差別，原因可能在于分開進行角區格和中區格火災試驗，角區格試驗后，中區格出現少許裂縫[12]，上述裂縫可能對板溫及變形有一定影響。由于模型限制，分析時未考慮上述行為影響，這一點有待研究。

2 數值模型

采用Vulcan程序，對框架結構中樓板進行溫度場模擬、變形和力學機理分析。溫度場分析時，沿板厚劃分24個矩形單元，如圖6(a)所示；其中，混凝土表面輻射系數取值為0.8，火焰輻射系數取值為0.75，表面吸收系數為1.0。混凝土熱工性能采用EC2模型[23]。

如圖6(b)～圖6(f)所示，結構分析時采用9節點厚板單元(幾何非線性)，每單元9個高斯點G1～G9，樓板劃分225單元(如編號17～21)，沿板厚劃分16層；鋼梁采用桿單元，且每個鋼梁沿跨度方向劃分為5個單元(如單元編號1～5)，沿其截面方向劃分為26單元；每鋼柱沿高度方向劃分為4單元。除特殊說明外，高溫混凝土和鋼筋(鋼材)力學性能均采用EC2模型，兩者粘結性能良好[23]。此外，不考慮樓板和鋼梁兩者粘結滑移。計算時，采用經典彌散裂縫模型模擬混凝土開裂，即采用混凝土最大拉應變破壞準則，即當任一高斯點上主應變超過最大拉應變則發生開裂。當一個方向開裂后，認為混凝土是正交各向異性材料。在單向開裂混凝土繼續加載，如果在垂直于裂縫方向上的拉應變超過最大拉應變，則發生雙向裂縫形式[20]。

對于試驗III，數值分析時，中柱所受初始集中荷載為125 kN，邊柱初始集中荷載為62.5 kN，角柱初始集中荷載為31.25 kN。此外，如圖6(g)所示，采用兩混凝土熱膨脹應變[23?24]，重點研究其對結構中樓板變形行為的影響規律。

3 計算結果

3.1 溫度分析

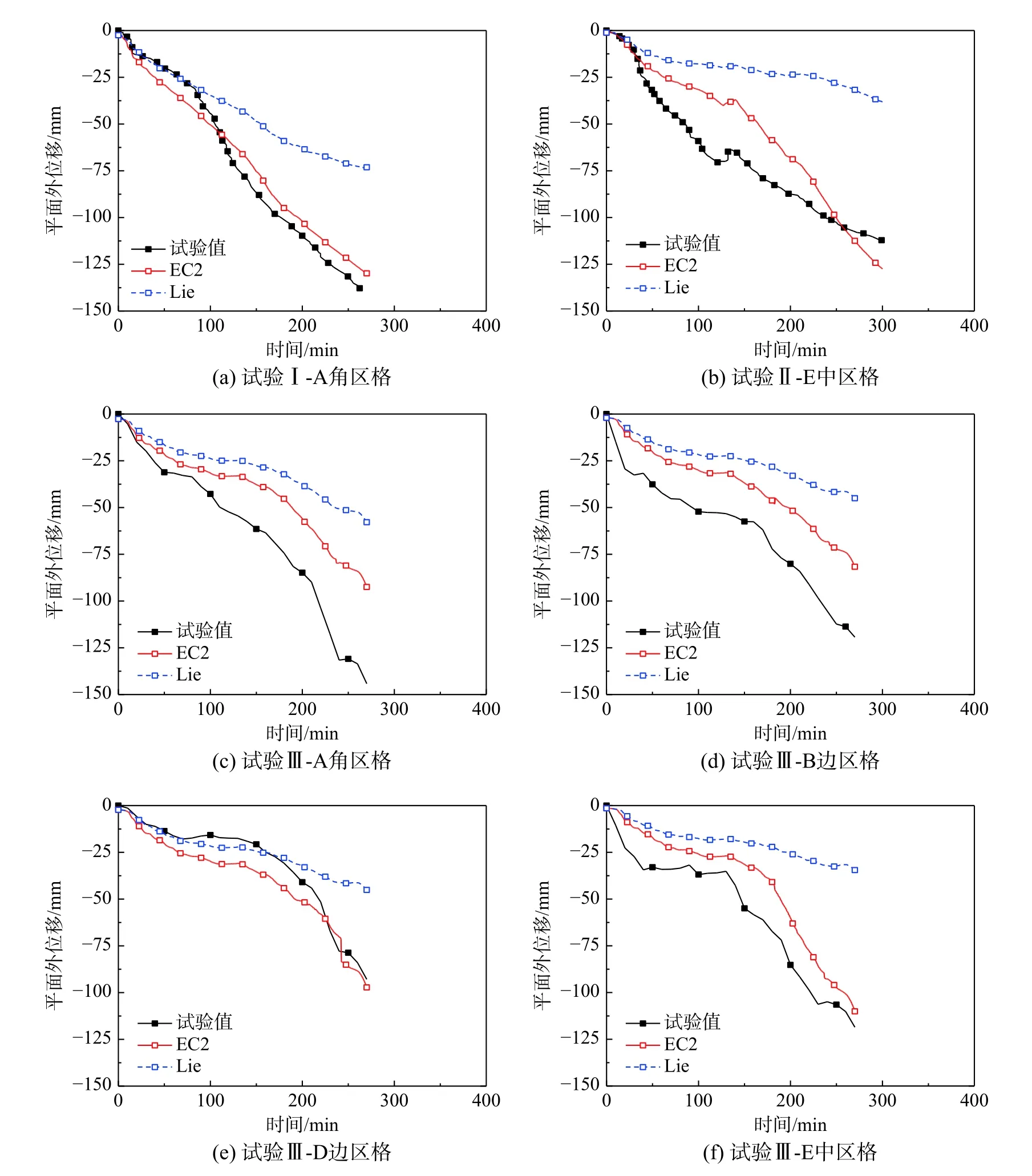
圖 5 試驗板變形計算結果與試驗變形對比Fig.5 Comparison of predicted and tested deflections of concrete tested slabs

圖3和圖4為混凝土、鋼筋和鋼梁溫度場計算結果和試驗結果對比情況。可知，有限元模擬結果與試驗結果吻合較好，變化趨勢較為一致，溫度分析較為合理。

3.2 裂縫分析

圖7(a)～圖7(c)為試驗I、II和III板頂試驗裂縫與數值分析所得彌散裂縫對比情況。可知，對于每個試驗工況，彌散裂縫與試驗板裂縫形式較為一致。

對于試驗I，A角區格整體表現為對角U型裂縫，即靠近兩內邊梁位置裂縫較多(負彎矩作用)，臨近角柱位置多為短小斜裂縫，板中區域裂縫較少。對于其他未受火板格，文獻[12]未給出；計算表明兩相鄰邊區格(D和B)和中區格(E)會產生較多裂縫，原因在于受拉薄膜效應和熱膨脹作用，具體見下述。同時，對于其他較遠板格，基本沒有裂縫。數值分析表明，受火板格A板邊區域(高斯點)出現雙向彌散裂縫，板中區域未開裂，且非受火D和B板格多為單向彌散裂縫，可見模擬結果能夠反映試驗板整體裂縫分布。此外，可見在災后修復時，除了對受火跨進行加固，也要對相鄰非受火區格裂縫采取措施，特別是耐久性方面。

圖 6 試驗板溫度和結構分析單元模型 /mmFig.6 Element models used in the temperature and structural analysis of tested slabs

圖 7 三試驗裂縫與彌散裂縫對比Fig.7 Comparison between the experimental cracks and predicted smeared cracks of three tests

對于試驗板II，彌散裂縫樣式和試驗結果基本吻合(見圖7(b))。具體地，中區格板頂為環形裂縫(負彎矩)，且跨中區域裂縫較少(正彎矩)；此外，非受火角區格(A、C、G和I)出現45°對角線裂縫，且邊區格(B、D、F和H)出現若干條平行裂縫。數值表明，受火板格E周邊出現較多雙向彌散裂縫，跨中區域無彌散裂縫，其余非受火板格為單向彌散裂縫，最終形成沿板跨方向或45°方向通長裂縫。主要原因在于中區格溫度較高，向外膨脹；其他板格溫度較低，對中區格產生較強約束作用，進而非受火板格產生拉應力而開裂，后續薄膜機理分析也證明了這一點。

對于試驗III，彌散裂縫樣式基本較為合理(見圖7(c))，受火跨基本上表現為三種裂縫樣式，即對角裂縫(角區格)、對邊U型裂縫(邊區格)和環形裂縫(中區格)，且裂縫集中在內支座位置(負彎矩)，數值結果表現為雙向彌散裂縫。一方面，跨中區域裂縫相對較少，原因在于受拉薄膜效應相對較小(見下述)。另一方面，對于非受火區格，裂縫集中在鋼梁上部樓板區域和板格內部，數值分析表現為少許雙向彌散裂縫(鋼梁頂部樓板)和較多單向彌散裂縫(板格內部)。

總之，在結構抗火設計中，應考慮受火跨數量和位置對各板格裂縫分布影響，且災后對各板格采用相應加固方法。

3.3 變形分析

各受火板格變形計算結果與試驗結果對比如圖5(a)～圖5(f)所示。可知，計算變形和試驗結果總體吻合較好。對于試驗III，與試驗變形相比，計算變形總體偏小，原因可能在于膨脹應變取值。對比可知，混凝土熱膨脹應變對受火板格變形有決定性影響，即較大膨脹應變引起較大跨中變形，特別是約束作用較強中區格。例如，對于試驗II(III)的中區格，停火時，EC2和Lie兩模型所得計算變形值分別為?127.5 mm(?38.2 mm)和?110.1 mm(?34.5 mm)。可見，降低混凝土熱膨脹性能或采用熱膨脹性能較小混凝土，有助于降低構件變形和提高其抗火性能。

圖8(a)～圖8(d)為試驗III三鋼梁平面外水平和豎向變形計算值和試驗值對比情況。對于未受火邊梁L1，計算值和試驗值吻合較好。由圖8(c)和圖8(d)可知，兩鋼梁位移-時間計算曲線與試驗曲線差異較大，主要原因在于鋼梁采用桿件單元模型，無法準確模擬鋼梁局部屈曲行為、節點上下翼緣斷裂行為和節點處螺栓滑移等，模型有待于改進和細化(如殼單元)。值得指出的是，鋼梁變形準確模擬(塑性鉸)對樓板薄膜機理及破壞模式產生有重要影響，且涉及鋼梁和樓板破壞順序。具體地，鋼梁過早破壞，樓板失去有效支撐，其不會產生薄膜效應，否則其會產生薄膜效應[25]。

此外，對比可知，混凝土膨脹應變(EC2和Lie)對鋼梁變形有一定影響，但相對較小。

3.4 樓板薄膜機理

在變形分析基礎上，對三試驗中(非)受火區格薄膜機理進行對比分析，如圖9(a)～圖11(d)所示。值得指出的是，對于每板格中薄膜效應(單位：N/mm)，紅(藍)色代表受拉(壓)薄膜效應，線長度表示薄膜大小。清晰可見，圖中0 min薄膜效應圖數據縮小10倍，其余圖中數據縮小100倍。

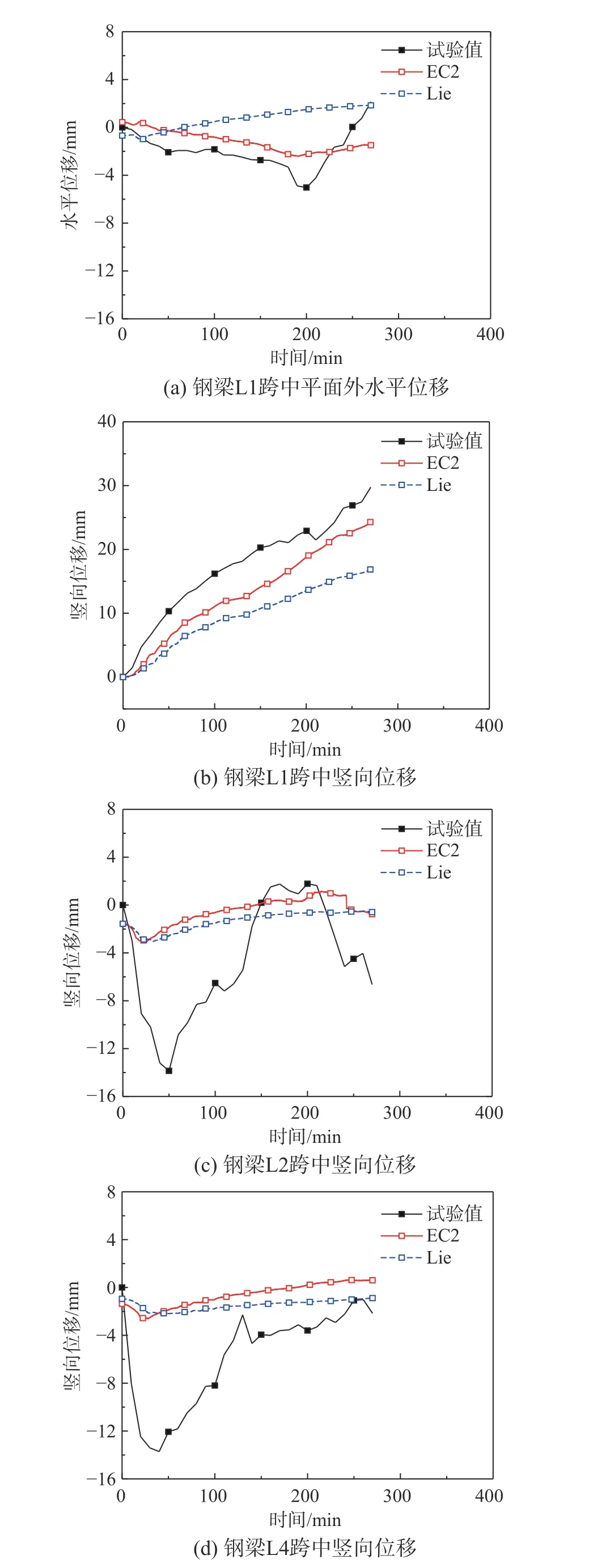
圖 8 鋼梁位移-時間計算曲線與試驗曲線對比Fig.8 Comparisons of the predicted and experimental deflections of the steel beams

圖 9 試驗I樓板不同時刻薄膜效應分布Fig.9 Membrane action distributions of Test I at different time

3.4.1 試驗I

圖9(a)～圖9(d)為不同時刻試驗I樓板薄膜效應圖。可知，邊界條件對受火板格薄膜效應分布有決定性影響，具體見下述。

0 min時，根據各板格薄膜力平均值來看，角區格薄膜壓力最大，其次是邊區格，中區格薄膜力最小。例如，對于角區格，兩方向均以受壓薄膜效應為主，且受壓薄膜力平均值為?11.5。對于中區格，薄膜效應相對較小，平均值為?0.66；對于邊區格，受壓薄膜效應主要平行與鋼梁方向，而另一方向薄膜效應相對較小。此外，與板格內受壓薄膜效應不同，各柱頂附近區域板格以受拉薄膜效應為主，且中柱附近薄膜力相對較大，平均值為65.5，其次是外邊柱板格區域，平均薄膜力為61.5，而角柱附近板區域，薄膜力最小，平均值為31.8。

一方面，隨著溫度升高，受火角區格受壓薄膜效應快速增大，特別是角柱和內部鋼梁附近位置；同時，該板格中心區域薄膜壓力逐漸降低，原因在于較大變形，受拉薄膜效應逐漸增加。例如，90 min(180 min和270 min)時，角區格A中心區域薄膜平均值為?311.5(?120.2和?29.6)。最終，受火角區格形成對角U型薄膜機制。另一方面，對于其他非受火板格，受拉薄膜效應區域有所擴大，如270 min，中區格平均受拉薄膜力為114.3；邊區格和角區格以受壓薄膜力為主，平均薄膜壓力分別為?78.1和?48.2。總之，隨著溫度升高，薄膜效應發展主要集中于受火角板格，而其余非受火板格拉壓薄膜效應機制基本變化較小。

3.4.2 試驗II

圖10(a)～圖10(c)為EC2模型所得中區格受火時樓板不同時刻(90 min、180 min和270 min)薄膜效應分布圖。值得指出的是，其0 min薄膜效應圖與圖9(a)一致，不再給出。

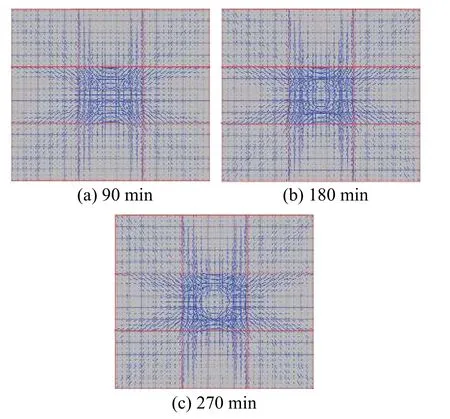
圖 10 試驗II樓板不同時刻薄膜效應分布Fig.10 Membrane action distributions of Test II at different time

由圖10(a)可知，樓板薄膜機理與圖9(b)薄膜分布明顯不同，進一步表明受火跨位置及其自身邊界條件對各板格薄膜效應分布有決定性影響。

一方面，薄膜效應圖基本對稱，即相同邊界條件板格薄膜機理基本相同，且存在三種薄膜分布樣式。另一方面，隨著溫度升高，薄膜樣式基本不變，但溫度(變形)對薄膜效應值大小和拉壓薄膜分布有重要影響。例如，對于中區格，90 min時以受壓薄膜效應為主，該板格受壓薄膜力變化范圍為?31.2～?1634.4，平均值為?430.6；對于四個邊區格，靠近受火板格位置，受壓薄膜力相對較大(?369.6)，而邊緣位置為受拉薄膜力(193.6)，因此該位置出現裂縫(平行內梁方向)；對于四個角區格，45°方向拉壓薄膜力較大，其他位置薄膜力較小，進而出現45°方向裂縫(見圖7(b))。

與試驗I類似(見圖9(a)～圖9(d))，隨著溫度升高，薄膜效應分布樣式基本維持不變，僅僅相應拉壓薄膜效應區域和大小發生變化，特別是受火中區格。如圖10(c)所示，由于變形增大，中區格跨中區域受壓薄膜力平均值為?349.1，而其邊緣薄膜壓力值為?858.6。

3.4.3 試驗III

圖11(a)～圖11(d)為EC2模型所得第二層樓板不同時刻薄膜效應分布圖。值得指出的是，該四區格內部鋼梁受火，而內部柱未受火。可見薄膜效應分布基本沿45°對角線對稱分布(見圖11(d))。

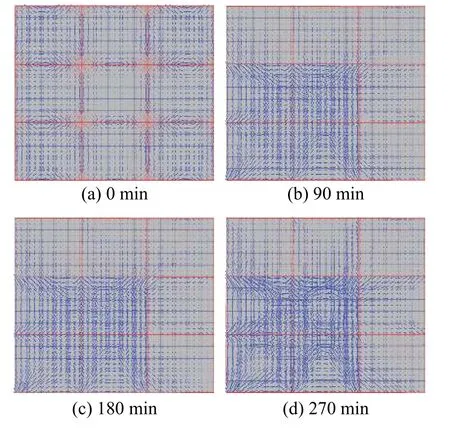
圖 11 試驗III樓板不同時刻薄膜效應分布Fig.11 Membrane action distributions of Test III at different time

圖11(a)薄膜效應分布樣式和數值基本與圖9(a)相同，可見柱軸力對樓板薄膜效應影響可忽略。一方面，由圖11(b)～圖11(d)可知，對于受火跨，存在三種薄膜效應分布樣式(見圖11(c))，即對角U型(角區格)、對邊U型(邊區格)和環形(中區格)。值得指出的是，90 min(180 min和270 min)時，中區格、邊區格和角區格跨中區域平均薄膜壓力為?354.1(?233.1和?190.5)、?448.2(?270.6和?222.7)和?210.7(?172.2和?110.9)。可見，板中受拉薄膜效應尚不明顯。

另一方面，對于非受火板格，兩個邊區格薄膜分布基本類似，而三個角區格薄膜分布存在較大差別。此外，值得指出的是，非受火板格鋼梁板頂附近區域存在受拉薄膜效應，進而該位置出現沿梁跨方向裂縫(見圖7(c))。

3.4.4 對比分析

由上可知，受火板格位置和數量對整體結構中樓板各板格薄膜效應分布有顯著影響。一方面，對于受火板格，其薄膜機理主要取決于自身邊界條件，進而包括三種薄膜機理，即環型薄膜效應(中區格)、對角U型薄膜效應(角區格)和對邊U型薄膜效應(邊區格)。

對于受火角板格(見圖9)，其兩外邊(垂直邊梁方向)無法提供較強的面內和轉動約束作用，該板格拉壓薄膜效應需要自相平衡，進而受壓薄膜效應(垂直邊梁方向)較弱，而平行邊梁方向受壓薄膜效應較強；對于該角板格兩內邊區域，周圍未升溫結構提供較強約束作用，該位置受壓薄膜力(雙向)相對較大，且受拉薄膜效應相對較大，進而主裂縫出現在該區域[12]。

對于受火中區格(見圖10)，周圍未升溫結構提供較強面內和轉動約束，且各方向不能自由膨脹，進而該板格邊緣出現較強雙向薄膜壓力；隨著變形增加，該板格中心區域逐漸出現受拉薄膜效應。對于受火邊區格(見圖11)，其僅一邊受面內約束作用較弱，進而該區域出現平行外邊緣受壓薄膜力；而其余三邊約束作用較強，表現為雙向受壓薄膜效應。

總之，一方面，在火災下樓板承載力或耐火極限分析時，應考慮邊界條件影響，而不能僅僅采用簡支板(環型)薄膜效應機制[25]。另一方面，對于非受火板格，其具體分布樣式明顯取決于受火跨位置和數量，薄膜效應值總體較小，但會引起混凝土開裂，且表現為不同裂縫分布。值得指出的是，若此時結構發生火災蔓延，上述裂縫會對結構抗火性能有重要影響，特別是隔熱性和完整性方面[9?10]，這一點有待深入研究。

3.5 鋼梁內力

3.5.1 跨中軸力

圖12(a)～圖12(c)為試驗I、II和III中鋼梁軸力-時間關系計算曲線。可知，鋼梁軸力隨時間逐漸增大，后期曲線較為平緩(平臺)。主要原因在于樓板受熱膨脹，鋼梁產生軸向變形，但其受到柱約束作用，致使梁軸力逐漸增大；隨著溫度增加，混凝土材料劣化和板跨中出現較大豎向變形，進而膨脹作用減弱，鋼梁軸力發展緩慢而出現平臺。相比受火跨區域鋼梁，非受火區域遠端位置鋼梁軸力相對較小，基本可以忽略。

例如，試驗I中非受火鋼梁L1和L2峰值軸力分別為1172.3 kN和917.9 kN，而其余鋼梁軸力很小，且火災過程中軸力基本不變。試驗II梁L4峰值軸力最大，其為925.9 kN，而L3、L5和L11峰值軸力相對較小，其分別為98.7 kN、115.1 kN和60.9 kN(平均值為91.6 kN)。

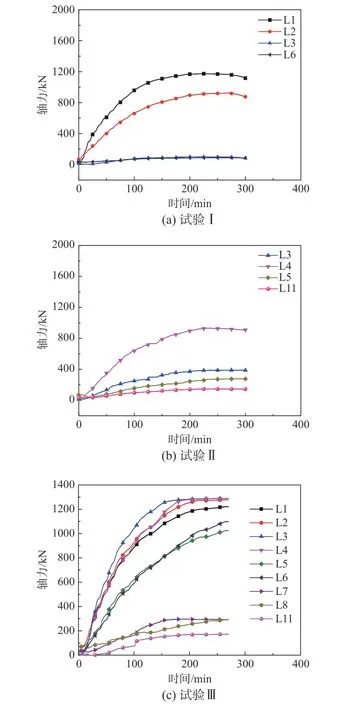
圖 12 試驗I～試驗III鋼梁軸力-時間關系曲線Fig.12 Beam axial force-time curve of Tests I, II, and III

對于試驗III，與上述兩試驗類似，試驗III中受火板格內部和周邊鋼梁峰值軸力早期逐漸增大后期逐漸平緩，平緩階段出現時間為161 min～270 min；停火時，L1、L2、L3、L4、L5和L6峰值軸力分別為1219.9 kN、1276.6 kN、1287.1 kN、1289.7 kN、1023.1 kN和1096.6 kN。四板格同時受火，鋼梁峰值軸力明顯高于前兩個試驗受火板格鋼梁軸力，相比試驗I梁L4，軸力峰值增幅達363.8 kN。對于非受火跨鋼梁軸力明顯較小，梁L8峰值軸力為293.4 kN。

總之，由于鋼梁膨脹作用受到周圍構件約束，進而鋼梁產生較大軸力，即出現反拱行為，其有助于降低鋼梁變形(見圖8(a)～圖8(d))和提高其抗火性能(見圖4(d))。不容置疑，上述力學行為可能導致火災下鋼梁出現過早屈曲破壞，特別是節點位置。因此，近年來，文獻[26]提出新的梁柱節點樣式，可大大降低升溫階段峰值軸力(即拱效應)，然而，這一點有必要開展深入研究，是否能夠在各火災階段(升溫、降溫及災后階段等)提高鋼梁在結構中抗火性能。另外，在結構中特別關鍵位置，對節點連接方式進行抗火性能優化設計，進而發揮不同節點在結構整體抗火性能方面(穩定性和結構倒塌)有利作用。

對于試驗I和II，邊梁L1和中梁L4達到峰值軸力時刻分別約為200 min和210 min，兩者峰值出現時刻基本相近；對于試驗III，邊梁和中梁軸力一直增加，直至試驗結束；可見火災工況對結構中鋼梁峰值軸力發展有重要影響。值得指出的是，這一行為與文獻[27]對火災下混凝土框架梁軸力分析結果較為一致。

由上可知，對于結構中鋼梁，需要進行大量火災工況分析(包括火災蔓延工況)，才可確定其最不利火災工況。值得指出的是，對于傳統結構設計方法，通過忽略約束作用進行構件承載力設計；然而，對于火災工況下，忽略熱膨脹行為和約束作用，基于傳統方法或單個構件火災試驗結果，可能過高或過低估計其在結構中抗火性能，有必要采用性能化設計方法[22]。

3.5.2 梁端彎矩

圖13(a)～圖13(c)為受火鋼梁梁端彎矩隨時間變化情況。其中，L1-D和L1-U代表L1鋼梁的下端和上端；L2-L和L2-R代表L2鋼梁的左端和右端。由圖可知，梁端彎矩均先增大至峰值，隨后逐漸趨于平緩。

對于試驗I，停火時，鋼梁L1上(下)端和L2鋼梁左(右)端彎矩達到峰值176.2 kN·m(?113.6 kN·m)和56.4 kN·m(?125.3 kN·m)，其他鋼梁梁端彎矩相對較小。對于試驗II，停火時，周邊鋼梁L4上(下)段和L6左(右)端彎矩分別為?118.8 kN·m(118.8 kN·m)和?116.3 kN·m(116.3 kN·m)，其余鋼梁梁端彎矩較小。

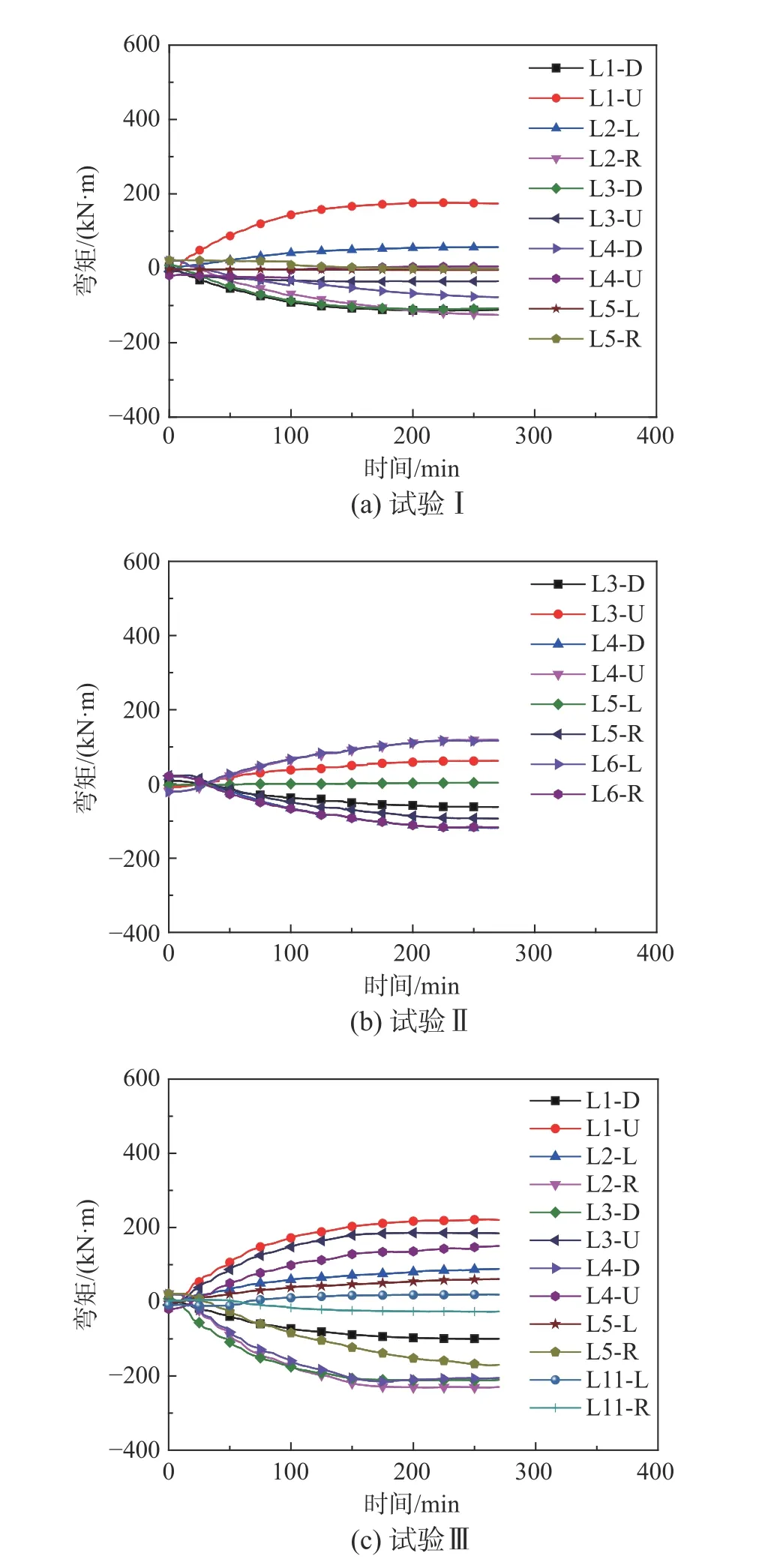
圖 13 試驗I～試驗III鋼梁梁端彎矩-時間關系曲線Fig.13 Beam-end moment-time curve of Tests I, II, and III

對于試驗III，停火時，受火鋼梁L2左(右)端和L4上(下)端彎矩分別為88.5 kN·m(?229.8 kN·m)和150.5 kN·m(?205.4 kN·m)。此外，鋼梁L1和L3上(下)端 分 別 為?99.8 kN·m(220.3 kN·m)和184.4 kN·m(?210.7 kN·m)；鋼梁L5左(右)端分別為61.1 kN·m(?170.1 kN·m)。其他遠端鋼梁彎矩相對較小。明顯地，受火鋼梁兩梁端彎矩存在較大差別。

3.5.3 跨中彎矩

圖14(a)～圖14(c)為試驗I、II和III鋼梁跨中彎矩-時間計算曲線，即為鋼梁跨中單元節點彎矩值。由圖可知，一方面，受火跨板格鋼梁彎矩相對較大，非受火板格鋼梁彎矩相對較小。另一方面，對稱位置鋼梁跨中彎矩基本呈現對稱分布，且隨著溫度升高，跨中彎矩值逐漸增大，但后期增速明顯變緩，接近水平。明顯地，這一點與文獻[28]所得結論(彎矩先增大后減小)略有不同。

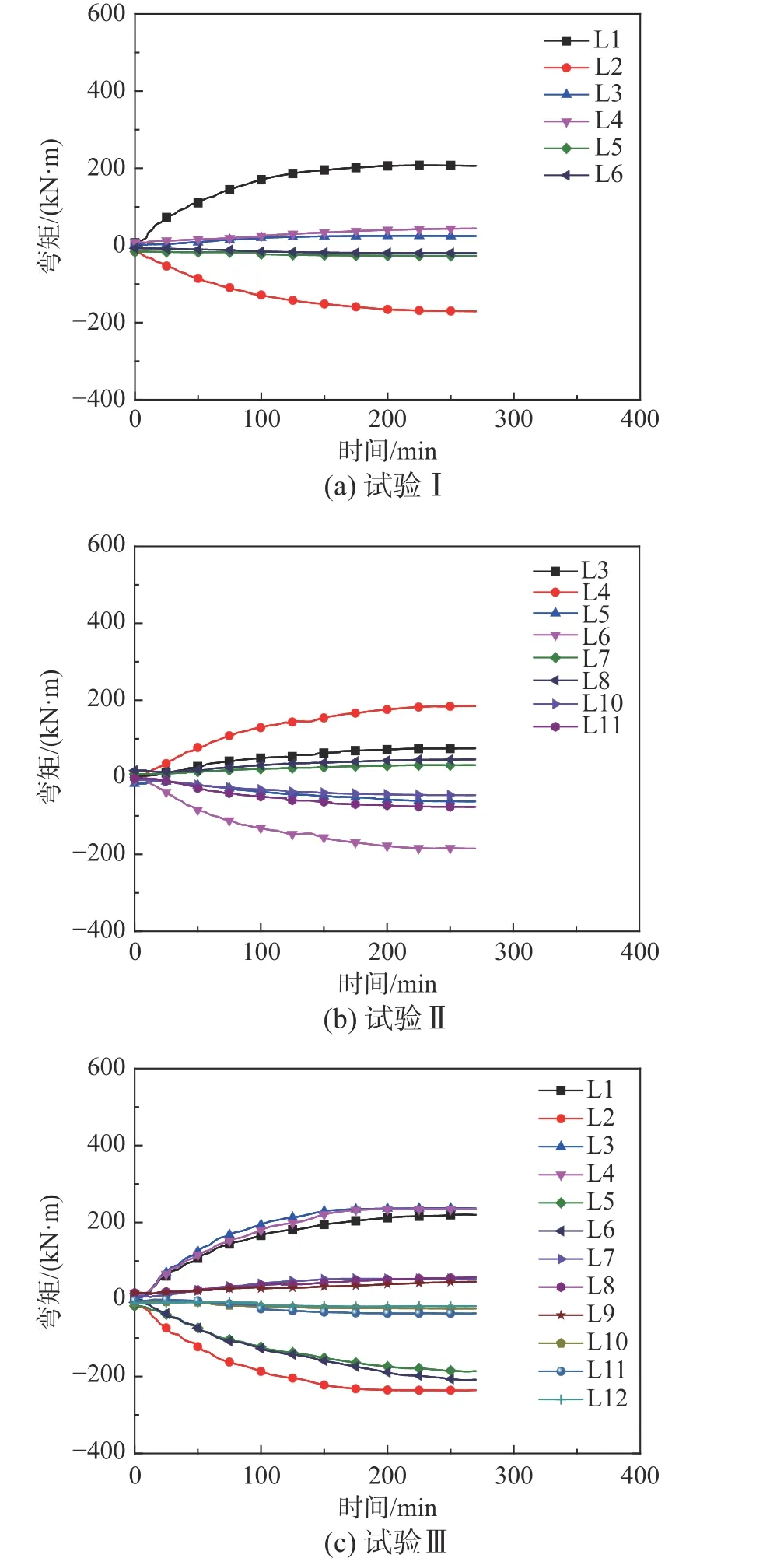
圖 14 試驗I～試驗III鋼梁跨中彎矩-時間關系曲線Fig.14 Beam moment-time curve of Tests I, II, and III

上述發展趨勢原因在于早期階段鋼梁升溫膨脹，但其受到周圍未升溫結構約束而產生較大軸力，且截面存在溫度梯度，產生附加彎矩，即彎矩逐漸增加；后期階段截面溫度一致，且強度和剛度損傷比膨脹作用影響更為顯著，跨中彎矩不再增加。值得指出的是，由于桿單元模型局限性，不能有效模擬鋼梁局部屈曲或反映節點性能等[29?30]，這一點有待深入研究。

對于試驗I，停火時，板格A兩未受火梁L1和L2，跨中最大彎矩分別為207.6 kN·m和?169.6 kN·m，明顯大于其他梁跨中彎矩，例如鋼梁L3(24.6 kN·m)和L5(27.1 kN·m)。同樣，試驗II和試驗III也存在類似規律，即受火板格鋼梁彎矩相對較大，例如受火梁L4相應峰值彎矩分別為185.2 kN·m和237.3 kN·m；相比受火跨板格鋼梁，非受火跨板格附近鋼梁彎矩相對較小，試驗III梁L8最大值約為58.2 kN·m。對比常溫狀態，可見鋼梁彎矩增加幅度約為14.3倍。

4 結論

本文對一3層足尺鋼框架結構頂層中區格、角區格和第二層樓板中四區格火災行為進行數值分析，研究了受火跨數量和位置對火災下樓板變形、裂縫分布、薄膜機理、鋼梁軸力和彎矩等影響規律，具體得出以下結論：

(1)混凝土熱膨脹應變對結構中樓板變形有重要影響；相比EC2混凝土熱膨脹應變，采用Lie膨脹應變所得受火板格跨中變形計算值相對較小。

(2)對于受火板格，其裂縫樣式取決于其自身邊界條件，且裂縫集中在負彎矩區域；對于非受火板格，其裂縫取決于受火板格位置和數量，即受火工況對其裂縫發展有決定性影響，而自身邊界條件影響較小。

(3)受火板格薄膜機理主要取決于自身邊界條件，分為三種薄膜機理，即環型、對角U型和對邊U型薄膜分布；對于受火板格，其板邊以受壓薄膜為主，而板中區域是否出現受拉薄膜效應，取決于自身變形情況；非受火板格可能出現拉壓薄膜效應，其數值相對較小，但對裂縫樣式有重要影響。

(4)受火板格周邊鋼梁以受壓為主，且火災早中期軸力和跨中彎矩增加較快，后期軸力和彎矩增長較為平緩；隨著受火板格增多，鋼梁軸力和彎矩峰值趨于增大。相比常溫工況，受火板格鋼梁內力增幅很大，而距離受火板格較遠鋼梁內力變化幅度相對較小。