魚類群體運動的元胞自動機模型中的最小勢能原理
陸興遠 袁衛鋒
群體運動是自然界中一種常見的生物行為.在過去的幾十年中,研究人員已經對鳥群、獸群、魚群和細菌菌落等不同的社會有機體的群體現象進行了廣泛的研究[1?5].眾多研究表明,某些規律對生物的群體行為起到關鍵作用.其中,“靠近被排斥,遠離被吸引”的規則對群體的分散、聚合和避免個體間碰撞以及躲避天敵攻擊有重要作用[6?8];流體力學和動力學原理也影響著群體的運動狀態.例如,Dai 等研究發現,魚類群體在運動中通過隊形來塑造能減小阻力的流場,使得個體耗能最小[9].
生物的群體運動是一種個體間協同相互作用的結果,群體中個體的信息傳遞對群體運動狀態起到重要作用[10].Gueron 和Couzin 等研究發現,群體信息在群體間是通過逐層傳遞的,個體的行為決策會受到相鄰個體的影響[11?12].群體中個體間交互協同的思想為智能機器人集群的自動控制提供了理論基礎.例如,Li 等受到生物系統的啟發,發明了群體顆粒機器人.雖然每個個體的運動是單一隨機的運動,但通過整個群體的協同,機器人群體可以朝著指定的激勵源方向移動[13],雷斌受生物群體行為啟發.應用仿生方法研究群體機器人的編隊控制,目標搜索,實現群體機器人間的協同控制[14].
在之前的研究中,研究人員大多在二維的假設條件下對群體運動進行研究,鮮有在三維的條件下研究群體運動,這與真實的群體狀態不符,并且之前的研究者提出的模型大多比較復雜.本研究構建了一個基于元胞自動機方法和最小勢能原理的簡潔三維模型,并通過數值模擬研究勢能在魚類群體中運動決策和個體間相互協同的作用以及對魚群在有限空間中形成旋轉運動狀態的群體機制的影響.
1 模型
元胞自動機是一種個體狀態由其鄰近個體狀態決定的算法[15].該方法已經被應用于流體力學,人流疏散等復雜場景的研究中[16?17].Pattanayak 等通過類元胞自動機方法的自航個體模型(Self-propelled particles)對群體運動的狀態轉換進行研究[18].本研究假定魚群的運動模式受勢能的支配,相應提出了魚類個體運動的勢函數并將之融合到元胞自動機中,建立了一種簡潔的三維模型以模擬魚群的運動.在真實魚類群體中,個體會以一定的速度游動,且速度不是恒定不變的.本研究假設模擬的虛擬魚個體以隨機的速度運動.虛擬魚的速度v定義為:v=v+α·Δv,其中α是[?1,1]的隨機數.在本研究建立的元胞自動機模型中,以半徑為v的球面上的點作為個體下一時間步可選擇的位置,如圖1 所示.個體將會選擇勢能最小的位置作為下一時間步的位置.本模型中每個位置的勢能均與個體的鄰居相關.
視覺是動物的共性,其對生物的群體行為和個體決策有著重要的影響.視覺影響個體感知周圍環境,是個體獲取信息的重要方式.研究表明,環境變化、鄰居數量和鄰居行為等都會影響個體行為決策[19].Ballerini 等研究發現個體在群體中與其他個體交流時并不是與整個群體交流,而是與其中的6~7 個鄰居交流[20].本研究假設個體的視覺為有限且不變的常值.如圖1 所示,Ri為個體的視覺距離;以θi為圓錐半角的圓錐體區域為個體的視角范圍,圓錐體以外的區域為個體的盲區.在本模型中,個體只會把在其視覺范圍之內距離其最近的N個鄰居作為參考鄰居,而不是整個魚群.個體在選擇參考鄰居時,如果視覺范圍內個體總數大于最大參考鄰居數N,就會以距離其最近的N個鄰居作為參考個體.
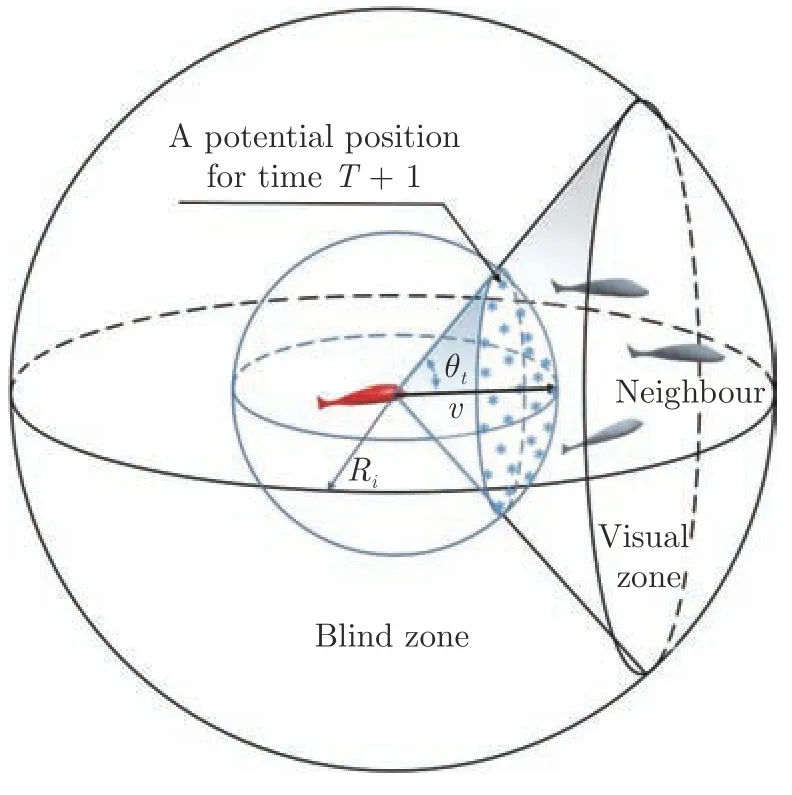
圖1 魚的模型Fig.1 Model of fish
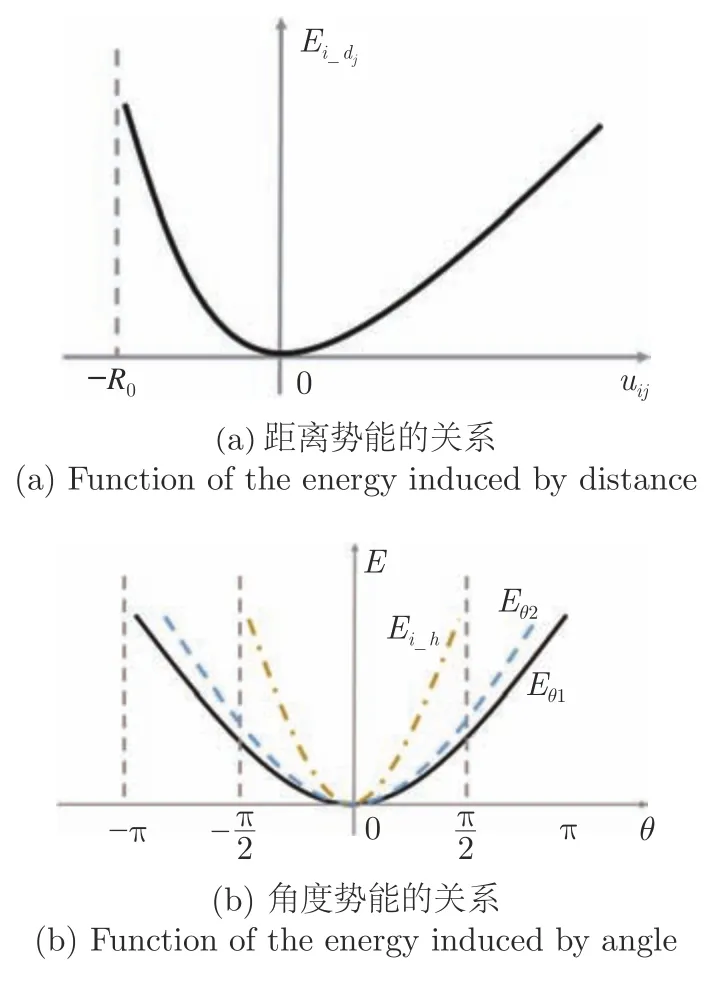
研究人員發現個體在群體中會因為相互間距離太近而相互排斥;如果個體間的距離太遠,個體間又會相互吸引.個體間存在相對穩定的距離[6?8,21].本模型中,假設個體i和參考鄰居j相互之間存在一個最佳距離R0,在這個位置上,個體i的距離勢能最小.當個體間距離小于R0時,個體間距離越小,個體間相互排斥越強烈;相反,當個體間距離大于R0時,隨著距離的增大,個體間的相互吸引程度增強,關系如式(2)和圖3 (a)所示.
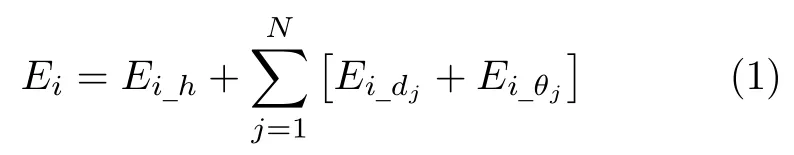
式(1)中,N為個體i的參考鄰居數量.
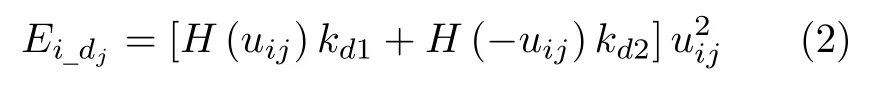
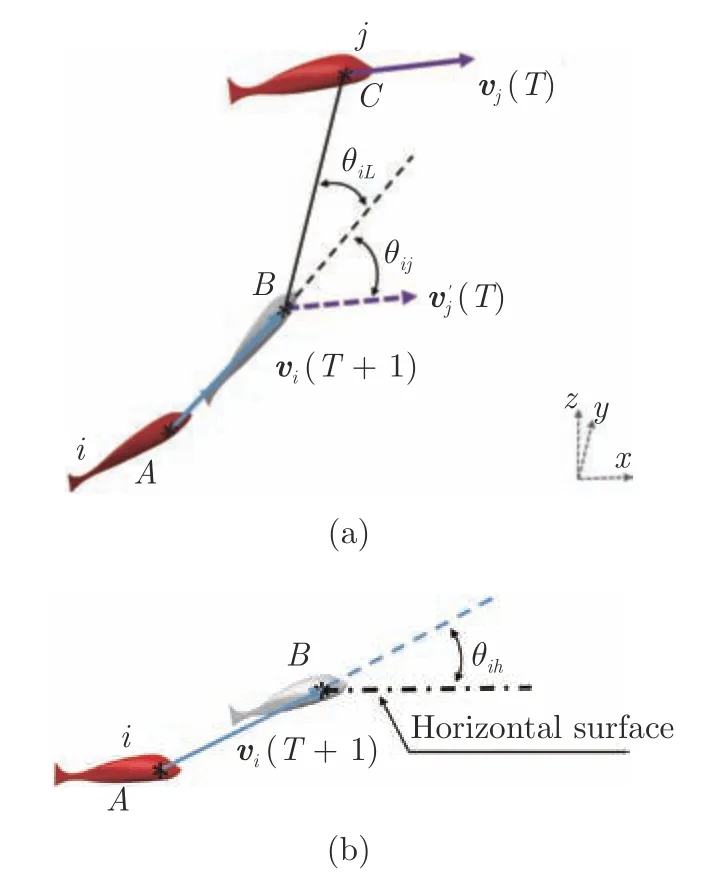
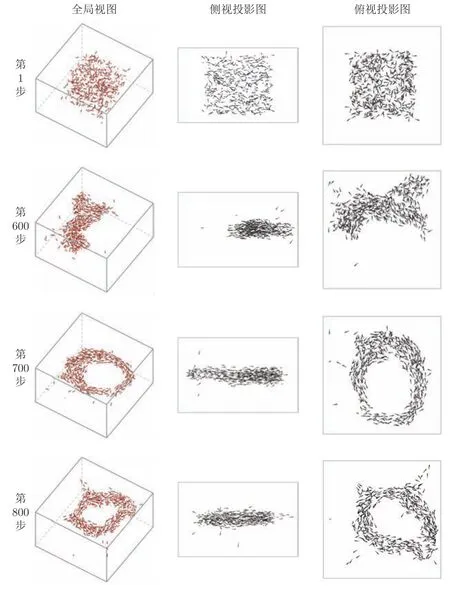
式(2)中,H代表(Heviside)階躍函數;uij=dij ?R0,R0為常數.kd1 式(3)、(4)中,kh、kθ1、kθ2、均為系數,θih表示個體i下一時間步的速度vi(T+1)矢量與水平面的夾角;θij表示個體i下一時間步的速度vi(T+1)和參考鄰居j當前時間步的速度vj(T)的矢量夾角;θiL表示個體i下一時間步的位置B和參考鄰居j當前時間步的位置C的連線與個體i下一時間步的速度vi(T+1)的夾角.關系如圖2 和圖3 (b)所示.圖2 (a)中為參考鄰居j當前時間步的運動方向vj(T)的平移,與vi(T+1)相交.圖2 (b)中點劃線為vi(T+1)在水平面的投影. 圖2 三維空間中虛擬魚中的角度關系Fig.2 The angular relationship in the potential energy of the fish in three-dimension 圖3 勢能函數的定義Fig.3 Functions defined for potential 本文把時間離散為若干個時間步,并把虛擬魚個體的下一時間步可能移動的空間范圍劃分為若干個位置點.虛擬魚群在每個時間步中遵循相同的規則.本文定義元胞自動機的規則如下面5 個步驟. 1)假設當前時間步為T.虛擬魚個體i確定視覺范圍內所有的參考鄰居和下一時間步所有可能的移動位置,如圖1 所示; 2)計算下一時間步T+1 所有可能移動位置的勢能,每個位置的勢能關系均如式(1)~(4)所示; 3)比較步驟2)中所有位置的勢能,確定勢能最小的位置,并把該位置作為下一時間步T+1的位置; 4)使用規則1)~3)遍歷虛擬魚群中所有的個體; 5)更新所有個體的位置,并重復步驟1)~5). 本研究對有限空間中紅斑馬魚群的運動狀態進行研究,構建了一個長寬高分別為120 cm,70 cm,80 cm 的玻璃缸和一個38 cm,25 cm,20 cm 的箱體,并購置了360 條紅斑馬魚,為了讓魚群適應實驗室的環境,在實驗室里飼養超過一個月,利用攝像機對紅斑馬魚群的運動狀態進行攝像記錄.值得注意的是,試驗用的大小水箱被放置在同一個實驗室中,除尺寸外其它條件相同.環境的變化對魚群是一種外來刺激,當把紅斑馬魚群從大箱轉移到小箱中,或者從小箱轉移到大箱中時,魚群都會出現轉圈的現象.如圖4 所示,當把魚群從大箱體轉移到小箱體中時,魚群會出現有序的旋轉運動狀態.在實驗中可以觀察到,紅斑馬魚群從無序的狀態逐漸轉變為有序的狀態,最后整個群體形成有序的旋轉運動狀態.從整個過程來看,魚群處于無序的混亂狀態下,群體中出現個別個體發起有序的運動,然后加入有序運動的個體不斷增多,群體運動狀態從無序的混亂狀態變為局部有序的帶狀運動狀態.當大部分個體參與到有序的群體運動中時,帶狀的群體運動狀態首尾相連,整個魚群形成環狀的旋轉運動狀態.有序群體狀態開始時,帶狀的群體形態的前部個體數量較多,較為密集,而群體尾部個體數量較少,較為稀疏.當最終形成環狀旋轉群體狀態時,整個群體中個體分布較為均勻. 圖4 真實紅斑馬魚群中的旋轉群體狀態Fig.4 Whirling state in real fish schools of red zebrafish 本研究對真實的紅斑馬魚群觀察發現,當魚群從大的箱體轉移到小的箱體中時,魚群會形成旋渦狀的群體形態.為了研究這種群體運動形成的機理,本文提出了一種魚類個體運動的勢函數,并基于最小勢能原理和元胞自動機方法建立了一個三維模型,如式(1)~(3)所示,通過數值模擬與紅斑馬魚群的運動形態對比,以驗證模型的合理性. 本模型假設參考鄰居j分別通過θiL、θij、uij影響個體i的位置、方向和相互之間的距離,并假設θih與個體i在深度方向上傾斜游動的角度相關.當相關系數處于適當的值時,模擬的虛擬魚群最終會演化成為旋渦狀的群體形態.模型中的各系數綜合地影響虛擬魚群的運動狀態,只有當各系數處于合適的取值范圍內時,模擬結果才會與觀察現象較好地吻合.本文中,對長寬高分別為30a,30a,20a的方形箱體中的500 條體長為a的虛擬魚進行數值模擬.當系數分別設置為kd1=4.0×105,kd2=2.2×109,kθ1=1.8×109,kθ2=9.0×109,kh=7.0×1010,R0=1.5a,且虛擬魚群中所有個體的位置和運動方向的初始狀態都隨機設置時(如圖5,第1 步),虛擬魚群經過若干時間步的運動后,演化為旋轉的群體形態,如圖5 所示.從整個演化過程看,虛擬魚群開始時處于隨機無序狀態,運動一段時間后群體中會形成局部有序的狀態,然后參與到有序運動的個體逐漸增多,原來帶狀的群體形態逐漸變長,最后帶狀群體形態首尾相連形成環形的旋轉運動形態,最終大部分個體參與到有序的旋轉運動中,整個虛擬魚群形成比較穩定的旋渦狀群體運動狀態.值得注意的是,最終的旋轉運動狀態并不是所有的個體一直參與其中,而是存在個別個體脫離群體,運動到群體外部,也存在個別個體在脫離群體后,重新加入到旋轉的群體運動中.對比虛擬魚群與真實的紅斑馬魚群的旋轉運動狀態及其形成過程,表明了本模型的模擬現象與真實魚群現象相符. 圖5 數值模擬過程中旋轉的群體狀態Fig.5 Whirling state in numerical simulation 群體運動是個復雜的自然現象.仿真雖然可以總體上得到與觀察相吻合的現象,但是在仿真中將個體的運動與實際觀察進行定量比較是非常困難的[6],因此,本文通過對魚類群體運動的定性分析闡明所提出的模型的合理性.必須說明的是,勢能公式中權重系數的取值對魚群運動的模擬結果具有的影響,只有當權重系數選取合適時,才能達到模擬結果和試驗觀察吻合的情況.例如,參數kd2在范圍“8.0×108~3.0×109”區間時,數值模擬能夠呈現魚群轉圈的現象,超出這個范圍,魚群運動很難出現穩定的旋轉狀態.如圖6 所示,在同一個時刻(第730 時間步),當kd2處于較小的值時,群體出現過于密集的狀態;而當kd2處于較大的值時,群體狀態較為混亂無序;只有當kd2處于合適的范圍內時,模擬的效果與觀察到的現象比較吻合.另一方面,kd2參數取值區間跨越一個數量級,說明利用本文模型對魚群定性研究時,模擬結果對參數的具體數值不敏感,這種穩定性有利于通過模擬獲取魚群運動的共有特性.在本文模型的基礎上,不同的權重系數取值會導致模擬中出現更多的魚群運動形態,從而有可能為群體運動研究提供新的關注點.從這個意義上講,結合最小能量原理而建立的元胞自動機模型可以被看作一個描述魚類群體運動的理論框架,而模型中具體參數的確定,需要更加廣泛和深入的研究. 圖6 kd2 取值不同時虛擬魚群在第730 時間步的狀態Fig.6 The status of fish schools at 730th time step subject to different kd2 values 本文對紅斑馬魚群在有限空間中的運動形態進行研究,假設魚群中每個個體在運動過程中總是試圖保持自身的勢能最小,相應提出了魚類個體運動的勢函數并將之融合到元胞自動機中以模擬魚群的運動.本研究發現:1)參考鄰居j分別通過θiL、θij、uij影響個體i的位置、方向和相互之間的距離;θih與個體i在深度方向上傾斜游動的角度相關.當相關系數處于適當的值時,虛擬魚群最終可能演化成為旋轉運動狀態.2)參考鄰居數量N的值與群體中個體數量有關,個體數量增多,參考鄰居的個體數量也會增多.當參考鄰居數量N在4~10 個個體之間時,魚群均可能出現旋轉運動狀態.本研究實驗觀察到的現象與數值模擬現象具有較好的一致性,并且本模型具有較好的魯棒性,二者證明了本模型能夠正確反映有限空間中魚類群體旋轉運動的形成機理.本模型有望應用于智能水下機器人或空中無人機集群控制中. 本文將能量最小原理和元胞自動機結合,提出了一種數值模型,通過調試模型中各參數的數值,能夠模擬出魚群運動的一些規律,說明能量最小原理有可能是魚類群體運動需要遵守的一個基本原理.本研究的意義在于該模型為研究魚類或其他生物的群體運動提供了一個數值計算的理論框架,有助于后續研究在此框架的基礎上進一步揭示群體和其所處環境之間的物理關系對群體運動特性的影響規律.本文僅針對包含同種個體的魚群的運動形態進行了研究,而自然界中常有不同魚類群體共存的現象,對不同生物群體間相互作用機理的研究將更具挑戰性和理論價值.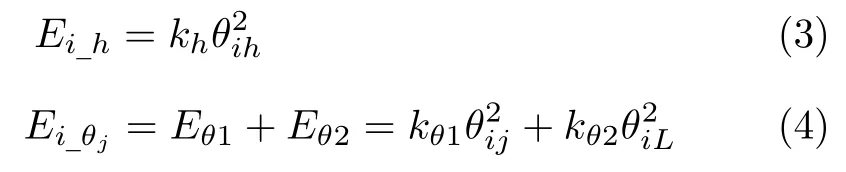
2 元胞自動機規則
3 實驗

4 模擬

5 結論

