基于柔性鉸鏈的低頻FBG加速度傳感器

邱忠超，王業偉，滕云田，張晉銓，洪 利

(1.防災科技學院 電子科學與控制工程學院， 河北 廊坊 101601； 2.中國地震局地球物理研究所，北京 100081)

加速度檢測是地震監測、結構健康監測以及資源勘探等領域的重要技術手段[1-3]。傳統加速度傳感器大多結構復雜、壽命較短，且易受環境影響，嚴重制約其在工程中的應用[4-6]。光纖布拉格光柵(FBG)振動傳感器因其體積小、靈敏度高、能夠抗電磁干擾、易組網等優點在加速度檢測工程應用中擁有廣闊的前景[7-8]。

梁磊等[9]提出一種橢圓鉸鏈光纖光柵加速度傳感器，橢圓鉸鏈和質量塊組成加速度傳感器理論模型的彈簧質量系統，靈敏度為128 pm/g，可用于350 Hz以下的低頻微弱振動信號的實時監測。Bing Yan等[10]提出一種新型雙柔性鉸鏈光纖光柵加速度，即使在50 g的沖擊載荷下，結構的最大應變仍在屈服極限內，靈敏度為54 pm/g。戴玉堂等[11]設計一種用于中高頻振動測量的雙鉸鏈加速度計，諧振頻率為3000 Hz，靈敏度為16.43 pm/g。Linessio等[12]提出了基于柔性鉸鏈結構的二維加速度傳感器，該傳感器具有溫度補償功能，用于二維加速度的測量。然而，這些傳感器存在靈敏度低等問題，使其難以在工程實際中應用。

針對光纖加速度傳感器靈敏度低的問題，提出一種基于柔性鉸鏈結構的低頻雙光纖光柵加速度傳感器。對其靈敏度和諧振頻率進行理論分析，采用MATLAB軟件對鉸鏈厚度、鉸鏈半徑、質量塊尺寸等結構參數進行分析和優化，利用ANSYS軟件進行結構靜應力和模態仿真，構建測試系統對傳感器實物進行性能測試實驗。

1 傳感器設計

1.1 傳感器結構

雙光纖光柵加速度傳感器為一體化結構，主要由L型剛性梁、柔性鉸鏈、FBG及質量塊四部分組成，如圖1所示。該傳感器是對稱式柔性鉸鏈結構，其中2根光纖光柵分別粘貼于結構上下兩側的溝槽內，并在粘貼時施加一定的預應力，避免光纖光柵產生啁啾效應。

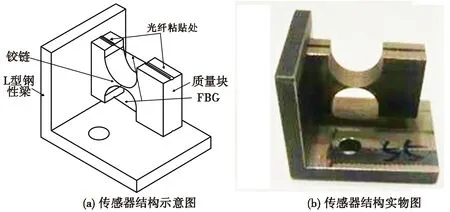
圖1 傳感器結構Fig.1 Sensor structure

當外界產生振動時，傳感器整體會隨振動信號運動。自由端的質量塊會隨慣性力上下振動，使固定其上的FBG受到來自質量塊的拉力，從而影響光纖內反射光的中心波長。鉸鏈結構上下對稱，兩根光纖光柵分別粘于結構上下兩側，當傳感器振動時上下兩端的形變方向相反，即兩根光纖一根處于拉伸狀態，一根處于收縮狀態。兩根光纖的反射光中心波長漂移量大小相等、方向相反，若將兩者差分，則可提高傳感器的靈敏度。

1.2 理論分析

傳感器結構振動模型如圖2所示，在振動信號產生的加速度a作用下，質量塊受慣性繞柔性鉸鏈中心微幅振動。

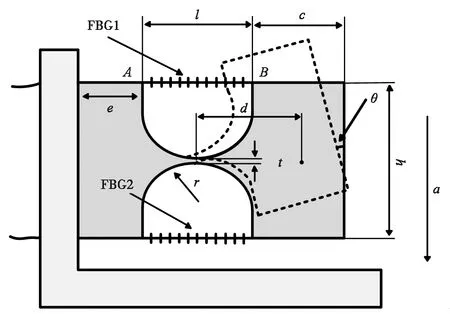
圖2 傳感器結構振動模型Fig.2 Vibration model of sensor structure

根據力矩平衡公式得

(1)

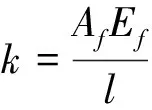
其中鉸鏈剛度K為

(2)

式中，E為材料的彈性模量，w為傳感器寬度，s=r/t，t為鉸鏈厚度。

柔性鉸鏈上、下兩根光纖可分別表示為FBG1、FBG2，兩根光纖的各項特性均相同。則當質量塊上下微幅振動時，上下兩根光纖由軸向應變產生的波長漂移量大小相同，方向相反，FBG1、FBG2的漂移量分別為

ΔλFBG1=ΔλB1+ΔλB2.

(3)

ΔλFBG2=-ΔλB1+ΔλB2.

(4)

式中，ΔλB1、ΔλB2分別為由光纖光柵軸向產生的應變ε和溫度變化T引起中心波長的漂移量。兩式做差分運算，即消除溫度變化T引起中心波長的漂移量ΔλB2的影響，得到FBG中心波長由應變ε引起的變化量，并且提高傳感器的靈敏度。

FBG加速度傳感器靈敏度S為由FBG應變引起的中心波長變化量與加速度a的比值，可得

(5)

式中，λB為光柵的中心波長，Pe為光纖有效彈光系數，一般為0.22，本文中的所指的靈敏度為峰-峰值靈敏度2S。

由運動學方程進一步可求出整個系統的諧振頻率為

(6)

式中，轉動慣量為J。諧振頻率f與傳感器的可用帶寬息息相關，傳感器諧振頻率越高，可用帶寬越寬，但傳感器靈敏度會顯著下降。

2 仿真分析

2.1 結構參數分析

由式(5)和(6)可知，傳感器的關鍵參數鉸鏈厚度t、鉸鏈半徑r、質量塊寬c、質量塊高h對其靈敏度與諧振頻率有較大影響，采用MATLAB對這4個參數進行分析。傳感器的材料為彈簧鋼，其彈性模量為210 GPa，密度為7 850 kg/m3。選取中心波長為1 555 nm、柵長為10 mm的光纖光柵，光纖有效長度l為12 mm。傳感器寬度為7 mm。

第一組分析鉸鏈厚度t和鉸鏈半徑r對傳感器靈敏度和諧振頻率的影響，令質量塊高h=17 mm，0.1 mm≤t≤0.8 mm，4 mm≤r≤8 mm，質量塊寬c分別為6 mm、10 mm和14 mm，結果如圖3所示。

由圖3可知，在不同的質量塊寬度下，鉸鏈厚度t對傳感器靈敏度和諧振頻率影響較大。鉸鏈厚度t越小、鉸鏈半徑r越大，則傳感器靈敏度越高、諧振頻率越小。當t=0.8 mm時，傳感器諧振頻率達到了1 000 Hz左右，靈敏度下降到只有50 pm/g。為滿足低頻測量的要求，將傳感器諧振頻率限制在200 Hz以內，需t<0.3 mm；為實現靈敏度達到200 pm/g以上，需要t<0.3 mm，同時r>5 mm。

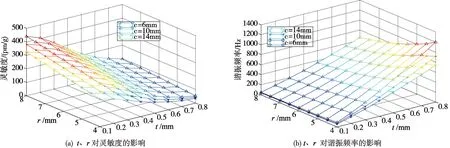
圖3 鉸鏈厚度t、鉸鏈半徑r對靈敏度和諧振頻率的影響Fig.3 The influence of hinge thickness t and hinge radius r on sensitivity and resonance frequency

第二組分析質量塊寬c和質量塊高h對傳感器靈敏度和諧振頻率的影響，令鉸鏈半徑r=6 mm，6 mm≤c≤14 mm，10 mm≤h≤20 mm，鉸鏈厚度t分別為0.2 mm、0.4 mm和0.6 mm，結果如圖4所示。

圖4 質量塊寬c、質量塊高h對靈敏度和諧振頻率的影響Fig.4 The influence of mass width c and mass height h on sensitivity and resonance frequency

由圖4可知，質量塊寬c對傳感器靈敏度和諧振頻率影響較大。傳感器的靈敏度隨質量塊寬c和質量塊高h的增大而增大，諧振頻率隨c和h的增大而減小。為滿足低頻測量和高靈敏度的要求，需c>9 mm，同時h>14 mm。

2.2 ANSYS仿真分析

由結構參數分析可知，鉸鏈厚度t和質量塊寬c發生微小變動時，會對傳感器靈敏度和諧振頻率產生顯著影響，而鉸鏈半徑r和質量塊高h在一定范圍變動時，對傳感器的影響相對較小。根據工程應用需要，保證諧振頻率低于200 Hz,靈敏度高于200 pm/g，同時考慮傳感器的尺寸和重量，選取t=0.2 mm，r=6 mm，c=10 mm，h=17 mm。采用ANSYS對結構進行靜應力以及模態仿真，有限元模型參數如表1所示。

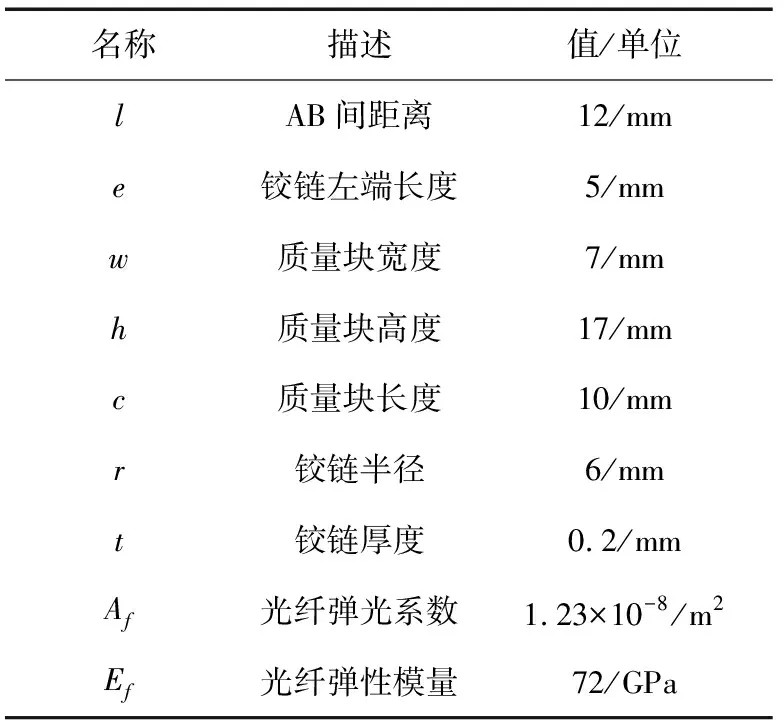
表1 FBG加速度傳感器參數Table 1 FBG acceleration sensor parameters

傳感器AB間的距離即為光柵的長度l，由于A點固定，B點位于質量塊左端，在傳感器振動過程中，光柵的形變量與B點的位移之間存在函數關系，不同頻率下B點位移可反映傳感器的幅頻特性。在ANSYS中，設置加速度大小為2 g，得到B點位移與諧響應頻率關系，如圖5所示，可知傳感器諧振頻率在130 Hz左右。

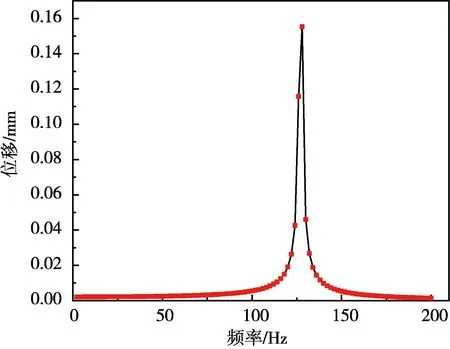
圖5 B點位移與諧響應頻率關系Fig.5 The relationship between B point displacement and harmonic response frequency

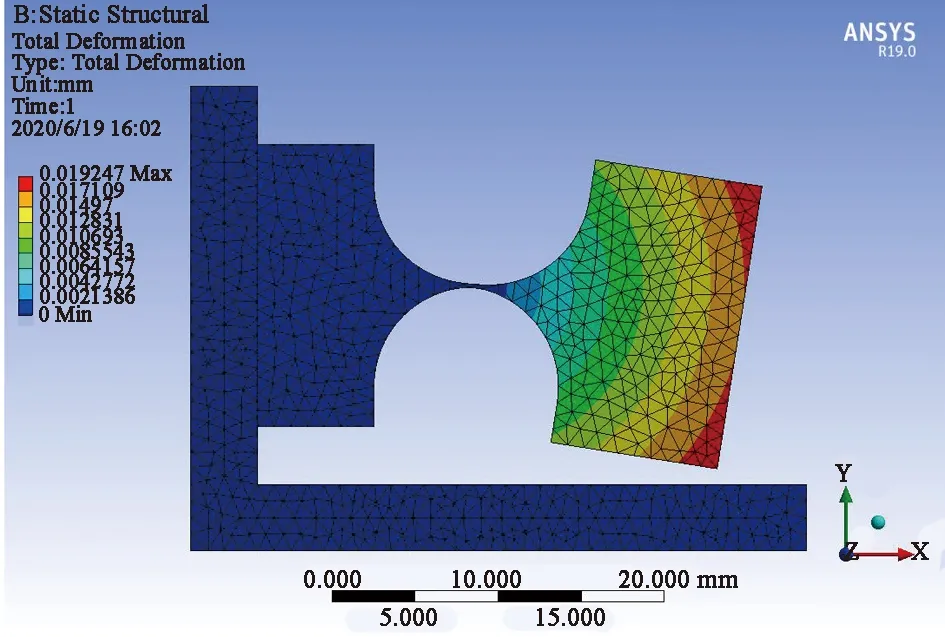
對傳感器底座施加固定約束，在質量塊的下表面施加大小為2 g的加速度，得到模型的等效應變圖，如圖6所示。可得自由端的形變量位移最大，從自由端到支撐端形變量逐漸減少。質量塊左端B點的形變量為0.012 mm左右，說明該傳感器結構可以實現外界振動信號的響應，并且形變量不影響光纖的物理性質，能夠保證傳感器的穩定性。

將模型放入模態分析模塊中，對底座施加固定約束，模型整體建立網格劃分。對模型進行模態分析，得到傳感器前4階模態頻率分別為131.14 Hz、1 023.10 Hz、2 440.10 Hz和4 614.00 Hz，1階模態如圖7所示。

由圖7可知，該結構的諧振頻率為131.14 Hz，且1階模態頻率與2、3、4階模態頻率相差較大，說明傳感器交叉耦合小，抗橫向干擾能力強。

3 傳感器測試實驗與分析

振動實驗系統由光源及信號放大系統、振動臺配套系統和信號解調系統組成，如圖8所示。振動臺配套系統包括振動臺、信號發生器、信號放大器；信號解調系統包括波長解調儀、計算機。寬帶光源發出的光經環形器輸送至加速度傳感器，在光纖光柵中心波長處一定范圍的光被反射回來，最終輸送至解調儀，解調出光波波長變化所攜帶的信息。

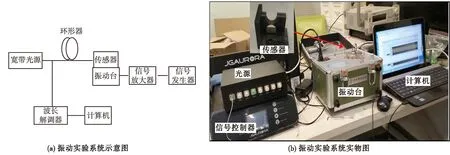
圖8 傳感器測試實驗系統Fig.8 Sensor test experimental system

3.1 響應特性測試

為測試傳感器響應特性，將振動臺的輸出頻率設定為20 Hz，加速度設為10 m/s2，得到其輸出頻率對應光纖光柵加速度傳感器響應的時域曲線，如圖9所示。

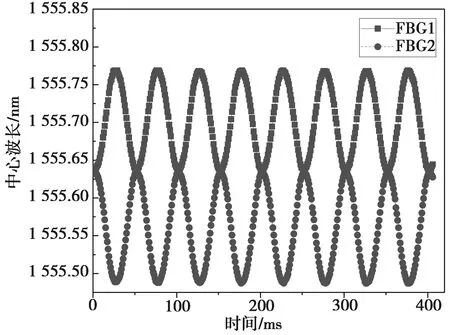
圖9 時域響應曲線Fig.9 Time domain response curve

由圖9可知，傳感器具有良好的輸出頻率響應，在每一時刻，光纖光柵加速度傳感器上、下兩根光纖的中心波長漂移量大小相同且方向相反，若將兩者差分，則可提高傳感器靈敏度。

給傳感器施加一個加速度大小為2 g的沖激載荷，得到傳感器其中一根光纖光柵FBG1在0.2 s內的沖激響應，如圖10所示。可知傳感器中心波長漂移量隨時間變化逐漸減小，傳感器具有較好的沖激響應。

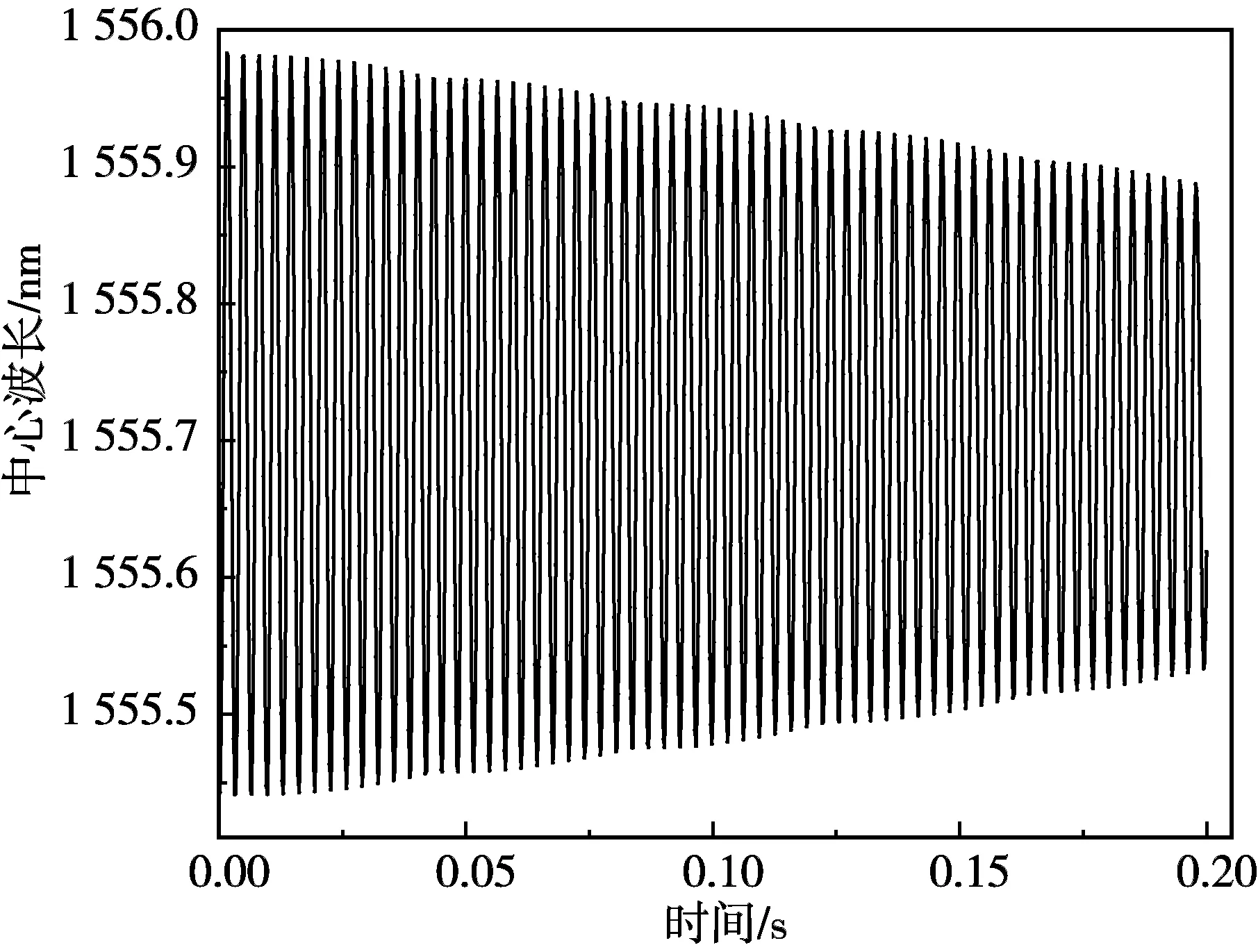
3.2 幅頻特性測試

設置振動臺加速度為5 m/s2，由信號發生器產生5～165 Hz的激勵，得到加速度傳感器幅頻響應曲線，如圖11所示。

由圖11可知，傳感器在90 Hz以下具有良好的平坦區。固有頻率為117 Hz，與仿真分析的理論值131 Hz相近，誤差可能是由于傳感器加工時的損耗以及光纖粘貼時施加預應力造成。

3.3 線性度測試

設定振動臺輸出頻率分別為20 Hz、40 Hz，以步長為1 m/s2改變加速度大小，變化范圍為3～13 m/s2，記錄2個不同頻率下FBG1和FBG2中心波長的變化，得到線性度擬合線，如圖12所示。

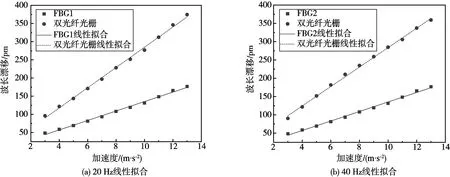
圖12 線性度擬合圖Fig.12 Linearity fitting graph

采集數據后分析處理得，輸入頻率在20 Hz時加速度傳感器單、雙光纖的靈敏度分別為130.1.3 pm/g和278.44 pm/g，40 Hz時單、雙光纖靈敏度分別為130.1 pm/g和265.78 pm/g，雙光纖20 Hz與40 Hz對應的線性度分別為R2=0.9968和R2=0.99738。結果表明，光纖光柵加速度傳感器的線性度良好，且雙光纖能達到增加靈敏度的作用。

實驗測得傳感器能夠測量最小加速度為0.1 m/s2，能測得最小振動頻率為5 Hz。與梁磊等[9]提出的橢圓鉸鏈光纖光柵加速度傳感器相比，在相同激勵下，該傳感器波長漂移量更大，靈敏度是其2倍，且雙光纖消除了溫度的影響。同時該傳感器諧振頻率更低，對100 Hz以下的低頻信號測量效果更好。

3.4 橫向抗干擾測試

將傳感器固定于振動臺上，設置加速度為10 m/s2，頻率為40 Hz的正弦激勵信號。記錄在相同振動環境下傳感器橫向振動與縱向振動光纖光柵中心波長漂移量的對比，結果如圖13所示。

圖13 橫向抗干擾實驗Fig.13 Horizontal anti-interference experiment

由圖13可知，傳感器的縱向響應與橫向響應分別為153 pm和7 pm，橫向光纖光柵中心波長漂移量僅為縱向的4.58%。說明傳感器在振動條件下可以看作是單自由度振動，具有較強的橫向抗干擾能力。

3.5 實驗誤差分析

實驗測得的傳感器靈敏度和諧振頻率與理論分析存在一定的誤差，主要由以下原因造成：1) 由于傳感器尺寸較小且鉸鏈結構部分較薄，在傳感器加工時會有一定的加工誤差；2) 鉸鏈的旋轉中心應該為某個微小區域，而非某一點，且粘合劑的用量、光纖光柵預應力的不同、器件加工誤差都會對鉸鏈的旋轉中心造成影響，進而影響傳感器的固有頻率和靈敏度；3) 實驗振動設備以及解調系統的精度都會對實驗數據造成一定的誤差。

4 結論

針對光纖加速度傳感器靈敏度低的問題，本文提出了一種基于柔性鉸鏈結構的低頻雙光纖光柵加速度傳感器。對其靈敏度和諧振頻率進行理論分析，采用MATLAB軟件對鉸鏈厚度、鉸鏈半徑、質量塊尺寸等結構參數進行分析和優化，利用ANSYS軟件進行結構靜應力和模態仿真，構建測試系統對傳感器實物進行性能測試實驗。結果表明，該傳感器的諧振頻率為117 Hz，在5～90 Hz的低頻段具有平坦的靈敏度響應，靈敏度約為278 pm/g，光纖中心波長漂移量與加速度有較好的線性相關性，橫向干擾程度小于5%。為光纖光柵加速度傳感器的工程應用提供借鑒。