斜交簡支梁橋地震位移響應特征與落座分析

杜 桁，徐略勤,2，鄧海容，夏 雪，孫榕徽

(1.重慶交通大學 土木工程學院，重慶 400074； 2.重慶交通大學，省部共建山區橋梁及隧道工程國家重點實驗室，重慶 400074)

近年來，我國橋梁建設事業飛速發展，橋梁數量日益增多。這其中，斜交梁橋因能更好地適應地形環境的差異性、改善道路的線形而得到廣泛采用，尤其在地表崎嶇的西部山區。然而，西部山區恰好與我國地震最活躍的斷裂帶相毗連，斜交梁橋由于其不規則的結構布置，地震響應遠比正交橋復雜，損壞程度也更為嚴重。可見，高烈度地震給西部山區的斜交梁橋帶來巨大的安全隱患。2008年汶川地震中的震害統計結果表明，斜交橋破壞比正交橋更為嚴重，有3/4的斜交橋都出現了中等以上震害[1]。斜交簡支梁橋是汶川震區最為常見的斜交橋型，其典型震害特征表現為梁體水平移位和平面轉動，部分橋梁甚至發生落座和落梁，伴隨著主梁位移震害的還包括：板式橡膠支座滑移、撕裂、脫空、卷邊；限位擋塊擠裂、剪斷、飛出以及伸縮縫錯位、擠壓變形、破壞等現象；而橋墩等下部結構出現結構性損傷的比例很低[2-3]。按照我國橋梁抗震設計規范[4]，斜交簡支梁橋屬于非規則橋梁，其抗震設計方法和抗震措施仍有待進一步完善。因此，研究這類橋梁在地震中的位移響應特征并進行落座分析具有重要的理論和工程參考意義。

近年來，國內外學者對斜交梁橋的地震響應和抗震性能已開展了不少研究，如Kun、Chen、陶源等[5-7]對斜交梁橋在伸縮縫和限位擋塊處的碰撞效應或雙向碰撞效應開展了數值模擬和試驗研究；Kwon、閆聚考、陳彥江等[8-10]對簡支斜交梁橋及正交橋主梁在地震作用下的平面旋轉機理及碰撞效應進行了探討；Noori、Jeon等[11-12]研究了地震輸入方向和角度對斜交梁橋地震響應和抗震性能的影響，得到了很多富有啟發的結論和成果。這些研究有力推動了斜交梁橋抗震理論和技術的進步，但不論是研究對象還是研究目的都各有側重，在針對斜交簡支梁橋地震位移響應特征與落座方面仍十分欠缺，尤其是對斜交橋主梁落座特點的研究亟待開展。震害調查經驗表明，落座是橋梁最嚴重的震害表現之一，會中斷橋梁上、下部結構的傳力途徑，使得橋梁在地震中成為不穩定的機構，防止橋梁落座是抗震措施設計的重要方面，我國橋梁抗震規范[4]對這方面的條文規定仍非常薄弱。有鑒于此，本文以我國公路橋梁中最為常見的30m跨斜交簡支梁橋為研究對象，考慮橋梁結構中各種材料和接觸非線性因素，基于參數分析探討這類橋梁的地震位移響應特征，并結合斜交簡支梁橋的結構特點，研究其主梁落座的特點和機理問題，以期為這類橋梁的抗震設計和加固提供參考。

1 典型橋例與分析模型

1.1 橋例概況

結合汶川震害資料[1]，以我國高速公路上最為常見的30 m斜交簡支T梁橋作為研究對象。如圖1(a)所示，為了考慮邊界跨的影響，分析橋例的跨徑布置為5×30 m，主梁由5片C50預應力混凝土T梁組成，橋寬12.5 m，基本工況下主梁斜交角為30°。每片T梁的兩端各設置1個GYZ D300×96板式橡膠支座。雙柱圓墩高15 m，直徑為1.8 m，墩柱頂設蓋梁，蓋梁兩端設鋼筋混凝土限位擋塊，墩柱和蓋梁均采用C35混凝土，墩柱縱筋為30根HRB40028熱軋鋼筋，箍筋采用HRB40010光圓鋼筋。橋墩基礎采用樁柱式基礎，樁徑為2.0m，橋例平面和斷面布置詳見圖1(b)和(c)。

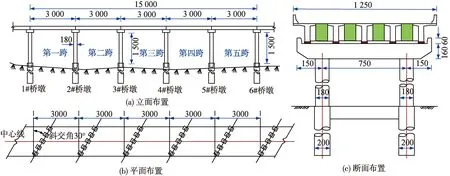
圖1 橋例布置(單位：cm)Fig.1 Bridge layout(Unit：cm)

1.2 分析模型

采用SAP2000程序建立有限元模型，斜交主梁按照梁格法模擬，其中，T梁采用線彈性梁單元模擬，T梁間的橫向聯系采用虛擬梁單元模擬，縱梁與虛擬橫梁形成斜交網格，如圖2(a)所示。蓋梁采用線彈性梁單元模擬，與墩柱間采用剛接。橋墩為延性構件，可能進入塑性狀態，對于框架墩來說墩頂和墩底均為潛在塑性鉸區，因此采用PMM纖維鉸來定義塑性鉸的特性，并按照現行規范[4]確定塑性鉸長度及其位置，如圖2(b)所示。本文研究對象為西部山區斜交簡支梁橋，所處地質條件一般較好，而且根據規范，中小跨徑梁橋的樁-土相互作用可忽略。因此，為了不給分析工作引入過多的不確定性，本文不考慮樁柱基礎的非線性行為，直接將墩底固結。

圖2 分析模型Fig.2 Analytical model

汶川震害顯示，限位擋塊對主梁地震位移響應的影響很大，因此模型中必須加以考慮。根據文獻[13]的研究，采用Multi-linear Plastic單元模擬其簡化滯回模型，并與Gap單元串聯來模擬擋塊與主梁間的碰撞現象，初始間隙為0.02m，如圖2(c)所示。

為了考慮梁體可能的平面旋轉，在梁端伸縮縫處設置5個碰撞單元，碰撞單元采用Gap單元的合并/張開來激活/鈍化鄰梁之間的碰撞作用，如圖2(d)所示。碰撞剛度參考Muthukumar等[14]的研究取主梁的軸向剛度，本文橋例為Kp=1.074×106kN/m，伸縮縫的初始間隙為0.1 m。

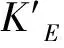
水平向剛度：

Kh=nGbAr/∑t

(1)

豎向剛度：

Kv=nEbAr/∑t

(2)

轉動剛度：

Kr=0.5nEbIb/∑t

(3)

式中：n為支座個數；Gb為支座剪切模量，根據規范[4]取1 200 kN/m2；Ar為支座橡膠板面積；∑t為橡膠層總厚度；Eb為支座豎向抗壓模量；Ib為支座沿彎曲方向的慣性矩。

1.3 分析工況

根據汶川震害調查統計情況[1]，選擇斜交簡支梁橋上部結構地震位移響應的關鍵影響因素：斜交角、擋塊強度和伸縮縫大小作為研究參數。其中，斜交角是主梁平面旋轉的重要影響因素[8-9]；擋塊強度是擋塊約束板式橡膠支座滑動行為的關鍵因素[13]；而伸縮縫大小則影響著相鄰梁體碰撞效應的程度[6-7]。表1列舉了本文參數分析的工況設置情況，其中，基準模型的斜交角為30°、擋塊強度取各墩恒載支反力的10%、支座摩擦系數取0.15、伸縮縫大小取0.1 m，其余各工況均在此基礎上改變其中一個參數的取值。

表1 分析工況設置Table 1 Details of analytical cases

1.4 地震動輸入

選取7組實際近場地震波，每組地震波包含2條水平向和1條豎向地震加速度記錄，如表2所示。為了方便對數據進行對比分析，將7組地震波中水平向最大峰值加速度PGA統一調整至0.4 g，其余2個方向的地震波按照相同的調幅系數進行調整。在進行非線性時程分析時，地震加速度時程波沿著橋梁的縱+橫+豎三向輸入，其中沿橋梁縱向輸入每組地震波中水平向PGA較大一條的加速度時程。

表2 地震波基本信息Table 2 Basic information of seismic records

2 地震位移響應特征分析

2.1 考慮斜交角的位移響應分析

圖3以No.2地震波為例給出了3#橋墩上右跨中支座縱、橫向力-位移響應曲線隨斜交角的變化情況。由圖3(a)～(b)可知，支座沿著縱、橫向都發生明顯的滑動行為，這種行為可以限制主梁地震慣性力向下部墩柱的傳遞，從而保護墩柱免遭結構性破壞，但同時也會導致主梁位移顯著增大；在縱橋向，當斜交角為30°時，支座滑動位移最大，而在橫橋向，當斜交角為60°時，支座滑動位移最大。由圖3(c)可見，以7條波的平均值來看，隨著斜交角的增大，支座縱向最大滑動位移先增后減，在斜交角為30°時出現最大值20.5 cm，在斜交角為60°時出現最小值5.8 cm，兩者相差71.7%；支座橫向最大滑動位移則先減后增，在斜交角為30°時出現最小值5.1 cm，在斜交角為60°時出現最大值24.4 cm，兩者相差79.1%；兩個方向的位移響應表現出明顯的耦合特征。

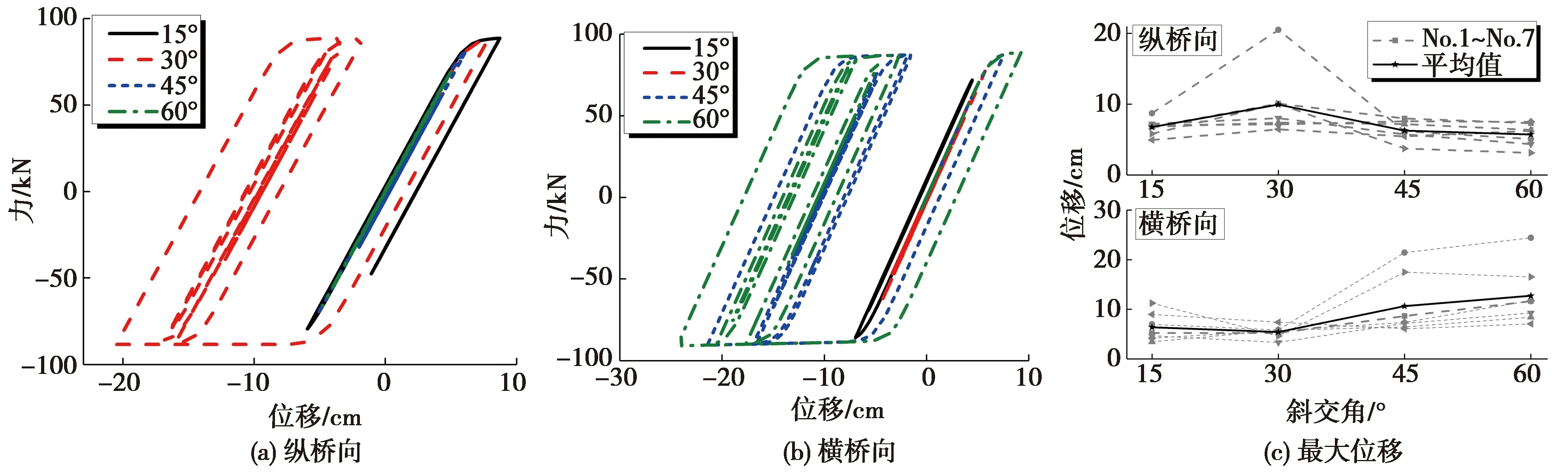
圖3 斜交角對支座位移的影響Fig.3 Effects of skew angles on bearing displacement

圖4以No.3地震波為例給出了第3跨(如圖1所示)左側梁端縱、橫向位移響應時程隨斜交角的變化情況。由圖可知，斜交角對梁端最大位移和殘余位移影響很大，隨著斜交角的增大，梁端最大縱向位移出現波動變化，當斜交角由15°增至30°時，梁端最大縱向位移由19.3 cm減為6.9 cm，減幅達到12.4 cm；梁端最大橫向位移則先增后減，當斜交角由15°增至30°時，梁端最大橫向位移由3.6 cm增至19.7 cm，增大了16.1 cm，之后再減小；可以看到梁端縱向位移的減少量與橫向位移的增加量較為接近。梁端最大縱向殘余位移先增后減，最大橫向殘余位移則先減后增。與支座位移響應相對應，主梁梁端位移在縱、橫向也表現出明顯的耦合特征。

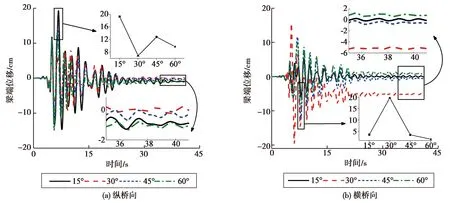
圖4 斜交角對梁端位移的影響Fig.4 Effects of skew angles on girder end displacement

圖5為第3跨主梁平面轉角包絡值隨斜交角的變化情況。可以看到，主梁平面轉角在不同地震波作用下的變化規律有所不同。但以平均值來看，隨著斜交角的增大，主梁平面轉角先增后減，在斜交角為30°時達到最大值。在斜交角為15°～60°范圍內，主梁平面轉角平均值的變化范圍為1.318×10-4rad～31.6×10-4rad，最大值是最小值的23.9倍。

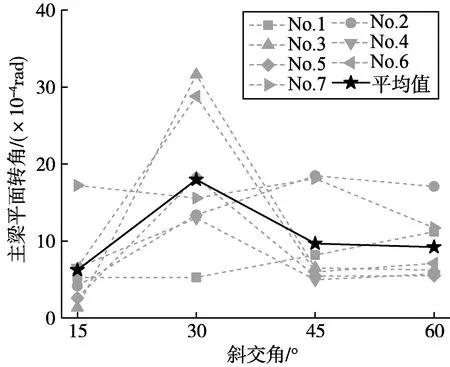
圖5 斜交角對主梁平面轉角的影響Fig.5 Effects of skew angles on girder rotations

綜合圖3～圖5的規律可以發現，斜交角大小是橋梁上部結構位移響應特征的重要影響因素。當斜交角小于30°時，支座縱向力-位移曲線出現了明顯的滯回環，滯回曲線相較于斜交角為45°和60°時更飽滿，且此時主梁梁端縱向殘余位移也明顯大于45°和60°時的殘余位移，表明在斜交角為30°時支座的縱橋向滑動行為最顯著，即：當斜交角小于30°時，上部結構的位移響應主要以縱橋向為主，且在30°時位移達到最大值。當斜交角大于30°后，支座縱向力-位移曲線幾乎呈線性，但在橫向卻發生了明顯的滑動行為，且梁端殘余位移在橫向上明顯更大，由此說明當斜交角大于30°后，上部結構的位移響應主要以橫橋向為主，且在60°時達到最大值。這一特征可為斜交簡支梁橋地震位移控制措施提供方向。

2.2 考慮擋塊強度的位移響應分析

圖6以No.2地震波為例給出了3#橋墩上右跨中支座縱、橫向力-位移響應曲線隨擋塊強度的變化情況。由圖6(a)～(b)可見，支座在縱向仍然發生了滑動行為，但隨著擋塊強度的增大，其滑動位移逐漸減小；而支座在橫向則幾乎沒有產生滑動行為，表明合理設計擋塊的強度具有良好的位移控制效果。而且與正交橋不同的是，在斜交簡支橋中，擋塊的限位效果不僅對支座的橫向位移響應有限制作用，對支座縱向響應也有較好的約束效果，其原因在于前文提及的斜交橋縱、橫向地震位移的耦合效應，以及擋塊對主梁平面轉動的約束作用，這點后文會有進一步分析。由圖6(c)可見，以7條波的平均值來看，隨著擋塊強度的增大，支座縱、橫向位移均逐漸減小，其中縱向位移的最大降幅為15.53%，橫向為9.33%，且橫向位移平均值顯著小于縱向。值得一提的是，當擋塊強度達30%恒載支反力時，支座縱、橫向位移曲線趨于平緩，表明當擋塊強度達到某一數值時，其對支座滑移位移的約束作用已趨于最大效果，此時不宜使用強度更大的擋塊，而應結合下部墩柱的損傷程度來確定擋塊合理的強度，因為擋塊也會將主梁的部分慣性力傳遞給下部墩柱。

圖6 擋塊強度對支座位移的影響Fig.6 Effects of retainer capacities on bearing displacement

圖7以No.2地震波為例給出了第3跨左側梁端縱、橫向位移響應隨擋塊強度的變化情況。由圖可知，梁端最大位移隨擋塊強度的增大略有下降，但總體上降幅較小，其原因在于梁端位移由支座位移和墩頂位移組成，擋塊可以降低支座的位移，但同時因向墩柱傳遞主梁慣性力而導致墩頂位移有所增大，兩者相互抵消，使得擋塊的限位效果在梁端位移響應上無法體現。梁端縱向殘余位移隨擋塊強度的增大而減小，橫向殘余位移隨強度增大而先增后略減，但總體上呈減小的規律。

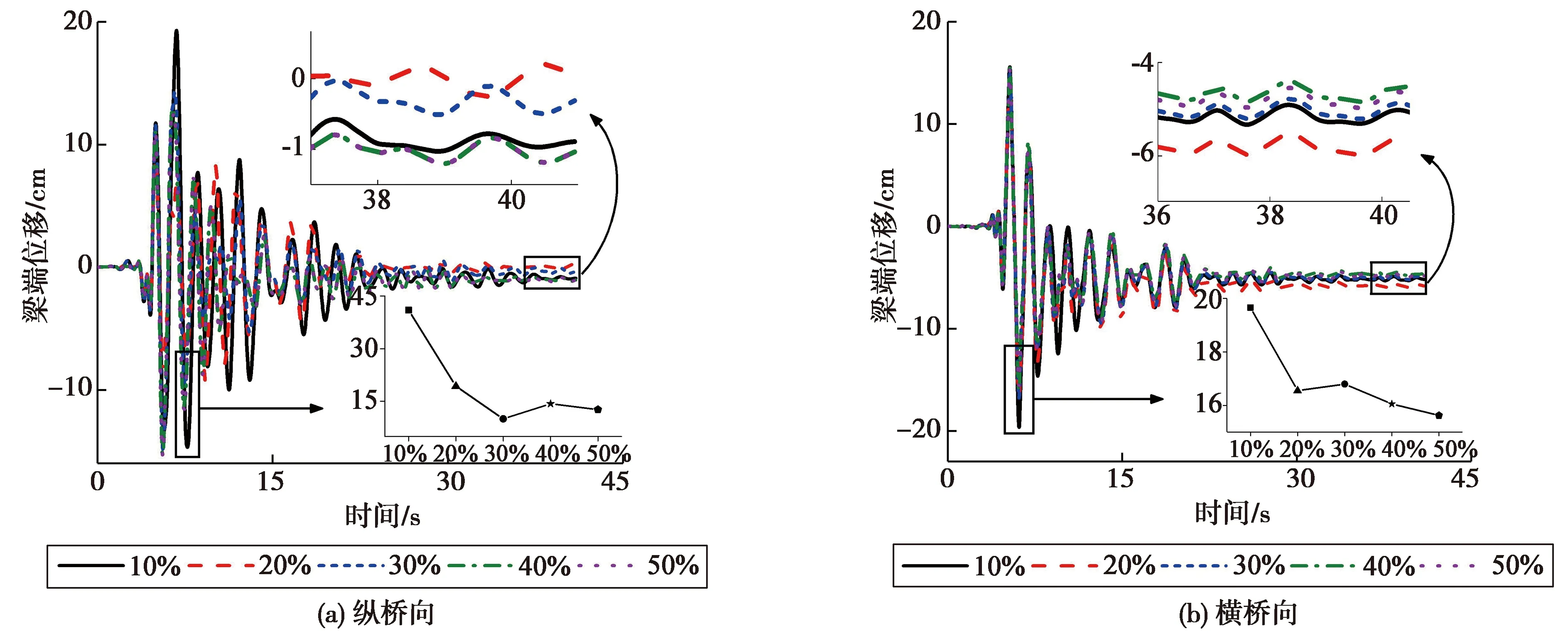
圖7 擋塊強度對梁端位移的影響Fig.7 Effects of retainer capacities on girder end displacement

圖8為第3跨主梁平面轉角包絡值隨擋塊強度的變化情況。以平均值來看，擋塊強度的增大可以有效地降低主梁的平面轉動，如當擋塊強度為10%恒載支反力時，主梁平面轉角平均值為23.27rad，當擋塊強度為50%恒載支反力時，主梁平面轉角平均值為16.73rad，下降28.12%。同樣可以看到，在本文橋例中，當擋塊強度達到30%時，主梁平面轉角的下降趨勢已明顯減緩，即擋塊的限制作用已經達到最高效果，表明擋塊強度并非越大越好。

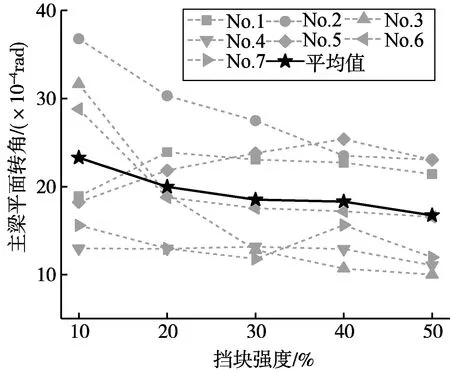
圖8 擋塊強度對主梁平面轉角的影響Fig.8 Effects of retainer capacities on girder rotations

2.3 考慮伸縮縫大小的位移響應分析

圖9以No.2地震波為例給出了3#橋墩上右跨中支座縱、橫向力-位移響應曲線隨伸縮縫大小的變化情況。相比斜交角和擋塊強度，伸縮縫大小對支座地震響應的影響要小得多，其原因可能與碰撞效應有關。伸縮縫大小會影響鄰梁碰撞程度，但由于主梁會同時受到左右兩側相鄰主梁的碰撞，在兩側碰撞效應接近的情況下，碰撞程度(伸縮縫大小)對支座地震響應的影響可能會被抵消。由圖9(a)～(b)可知，支座在縱橋向雖也發生了明顯的滑動行為，但隨伸縮縫大小的增大，其滑動位移幾乎沒有變化；而支座在橫橋向沒有產生滑動行為，位移響應略有下降。由圖9(c)可見，以平均值來看，隨著伸縮縫大小的增大，支座縱、橫向最大滑動位移略有減小，縱向最大位移由7.72cm降至7.40cm，橫向最大位移由8.55cm降為6.20cm。支座位移隨著伸縮縫增大反而下降的趨勢可能與所選支座位置和碰撞效應有關。由于同一橋墩處橫向各支座的位移響應有明顯區別，限于篇幅且便于后文落座分析，本文選取了橫橋向的中間支座(即主梁重心線處的支座)來說明各研究參數對支座地震響應的影響。為了進一步探討伸縮縫大小的影響，后文將專門分析碰撞效應的變化情況。

圖9 伸縮縫大小對支座位移的影響Fig.9 Effects of expansion joint size on bearing displacement

圖10以No.2地震波為例給出了第3跨左側梁端縱、橫向位移響應隨伸縮縫大小的變化情況。由圖可知，隨著伸縮縫間距的增大，梁端縱、橫向最大位移均增大，其中橫向最大位移先減而后增，但總體呈增大趨勢；梁端縱、橫向殘余位移也隨伸縮縫大小的增大而增大。這是由于伸縮縫大小的增大在縱橋向上為主梁提供了更大的位移空間，而斜交主梁的位移耦合效應使得梁端橫向位移也同時有所增大。

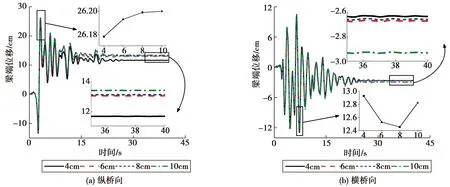
圖10 伸縮縫大小對梁端位移的影響Fig.10 Effects of expansion joint size on girder end displacement

在7組地震波下，各伸縮縫處的碰撞效應呈相似的變化規律，為便于討論，以No.1地震波的分析結果為例進行討論。圖11為4#墩上伸縮縫處的碰撞力分布的變化情況，由圖11(a)可見，同一伸縮縫處的碰撞力在橫橋向分布是不均勻的，越靠近橋面中心線越小，甚至為零，伸縮縫橫向兩側角點處的碰撞力則明顯更大，其原因在于斜交主梁在地震中產生了平面轉動，兩個角點處最容易與鄰梁發生接觸，因此最容易產生碰撞力，且兩個角點處的碰撞力本身也不相同。圖11(b)、(c)分別給出了1#和5#碰撞單元的碰撞力時程，可以看到，1#單元的最大碰撞力為1 668.86kN，而5#單元的最大碰撞力達4 457.74kN，是1#單元的2.67倍，且兩者出現的時間不同步。由于碰撞力是與位移正相關的，因此斜交主梁在地震中更容易沿著自身銳角端向橋面內發生轉動，而這種轉動又反過來增大了伸縮縫處不均勻的碰撞力分布，使主梁在伸縮縫處表現出“碰撞→增大轉動→不均勻碰撞力增大→轉動加劇”的循環過程。從伸縮縫大小的影響來看，同一伸縮縫處的碰撞單元表現出不同的規律，1#單元碰撞力隨著伸縮縫的增大而逐漸增大，增幅為39.7%；5#單元碰撞力隨著伸縮縫的增大而先減后增，最大值和最小值相差20.3%。從各單元碰撞力峰值來看，由于斜交橋存在不均勻碰撞現象，在本文的研究范圍內，伸縮縫為8cm時，碰撞力峰值是最小的。

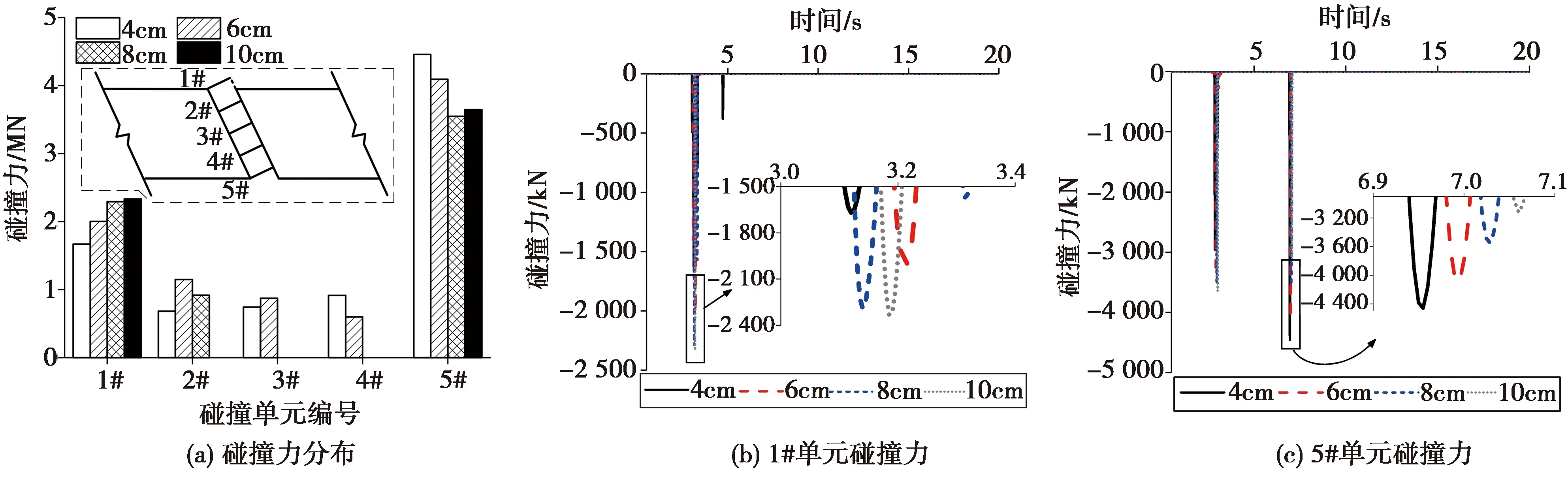
圖11 伸縮縫大小對碰撞力的影響Fig.11 Effects of expansion joint size on pounding forces

3 落座分析

前文分析表明，支座在地震中會發生滑動行為，若滑動位移過大則會導致主梁落座。實際工程中若主梁發生落座，則支座的傳力途徑將會被中斷，支座的滑動摩擦本構模型不再成立，但這個過程在數值模擬中很難精確實現。在主梁落座之前，一般可認為支座的本構模型是合理的[15]，因此從數值模擬的角度分析落座是可能的，但分析落梁則存在一定的困難，因為落梁往往發生在落座之后。圖12和表3給出了支座滑動狀態的判斷依據[16]，其中，D為支座與上部結構之間的相對位移；D0為支座的滑動臨界位移，D0=μ·N/Kh，符號意義同前文；D1為初始時刻梁底鋼板內邊緣至支座內邊緣的距離；D2為梁底鋼板內邊緣至支座中心線的距離；D3為梁底鋼板內邊緣至支座外邊緣的距離。

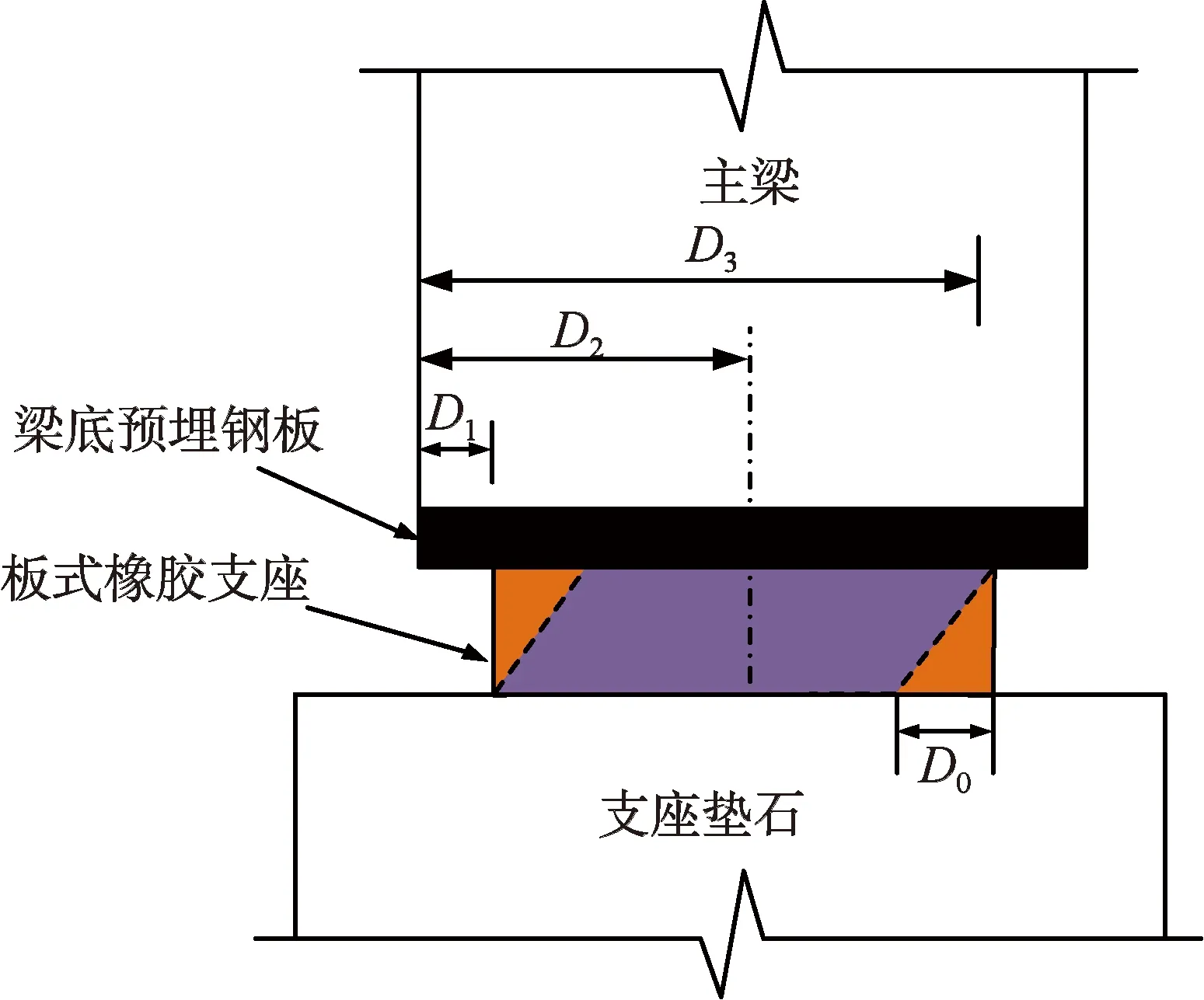
圖12 支座滑動狀態示意圖Fig.12 Diagram of the slide states of bearing

根據表3的指標，對前文各工況下的支座縱、橫向位移狀態進行分析，表4列舉了在No.2、No.5和No.7三組典型地震波作用下，3#墩上右跨中支座的滑動狀態，表中僅列出滑動更嚴重的那個方向的結果，并將“縱向輕微滑動”簡稱為 “輕滑-縱”，其他表述類似。

表3 支座滑動狀態指標Table 3 Indexes of the slide states of bearing

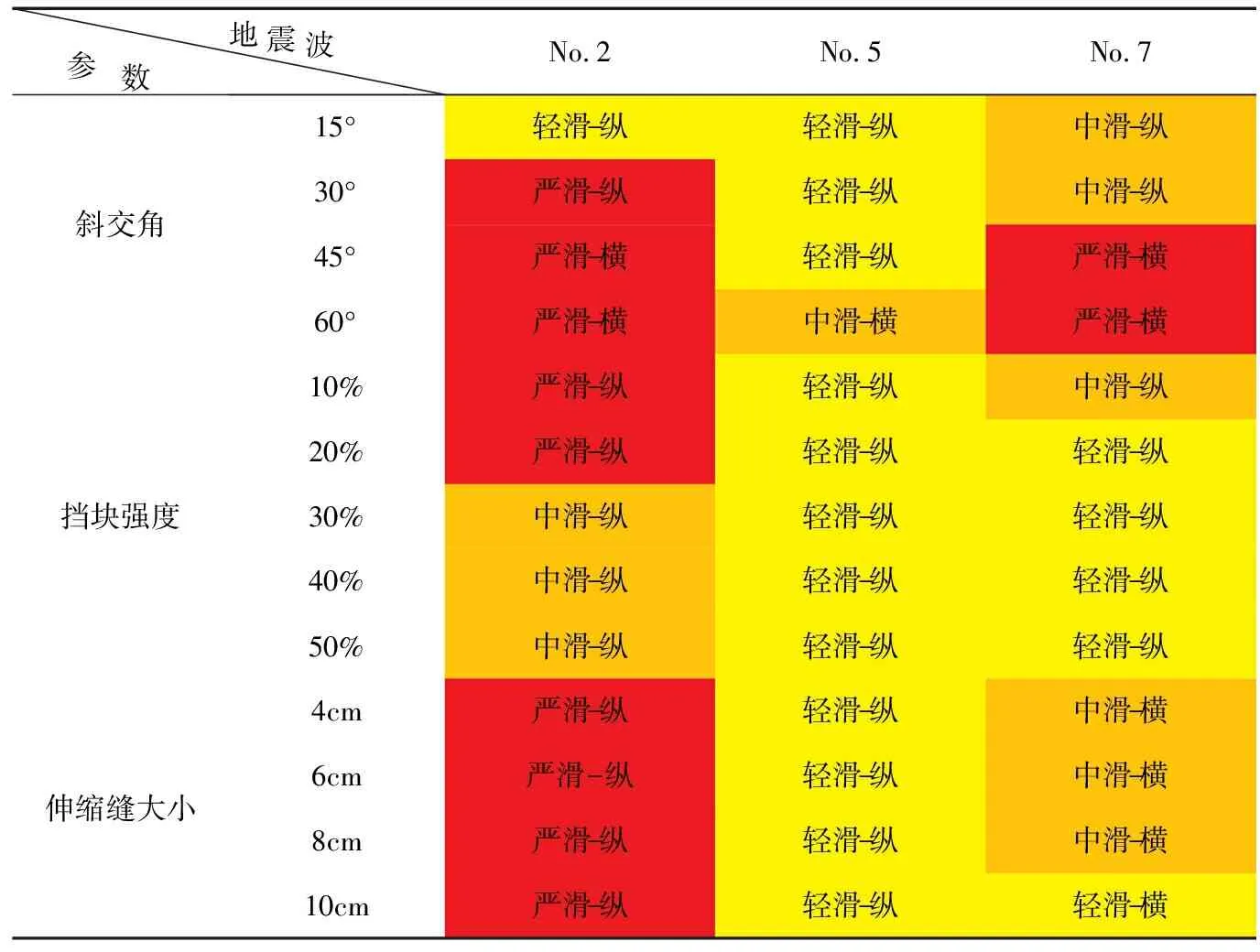
表4 支座滑動狀態結果Table 4 Results of the slide states of bearing

由表可知，當斜交角為15°～30°時，支座在縱向上產生更明顯的滑動行為；當斜交角為45°～60°時，支座的滑動方向逐漸轉為橫向。這與前文所述規律相符，即：當斜交角小于30°時，上部結構位移響應以縱向為主，當斜交角大于30°時則相反。地震作用下，斜交主梁的一端會與鄰跨抵緊，另一端則更易擺動，結構地震響應類似于循環荷載作用下的“棘輪效應”[17]，斜交角的增大加劇了擺動程度，使得支座在斜交角大于30°時橫向滑動更明顯。當擋塊強度由10%恒載支反力升至50%時，大多數地震波下的支座滑移程度由嚴重/中等降低為輕微滑動；且在擋塊強度大于30%之后滑動程度不再改變。幾乎所有地震波作用下的支座都發生縱向滑動，橫向幾乎不發生滑動或滑動程度很低，表明了擋塊的限位作用十分顯著，適當增大擋塊的強度可有效減輕支座的滑動狀態。伸縮縫大小對支座滑動狀態的影響并不顯著，在大多數地震波作用下伸縮縫大小并沒有改變支座的滑動狀態，但在個別地震波(如No.7)下，增大伸縮縫大小可在一定程度上減輕支座的滑移程度。值得一提的是，在本文的研究范圍內，中間支座并沒有出現落座情況(由于中支座位于主梁重心線上，主梁因此一般也不會出現落梁情況)。

圖13選取3個典型工況分析了斜交簡支梁橋第3跨主梁的位移響應特點，圖中支座的顏色與表4表示相同的滑動狀態。由圖可知，由于主梁發生平面轉動，各支座的滑動狀態有所不同，且在不同的斜交角和擋塊強度下，支座縱、橫向滑動的嚴重程度會發生轉換，但基本都存在如下趨勢：即斜交主梁在地震中更容易沿著自身銳角端向橋面內發生轉動，按照圖中的示意方向即逆時針轉動。因此，在實際工程中可以適當加強銳角端的擋塊強度，減輕主梁的平面轉動幅度，降低落座風險。

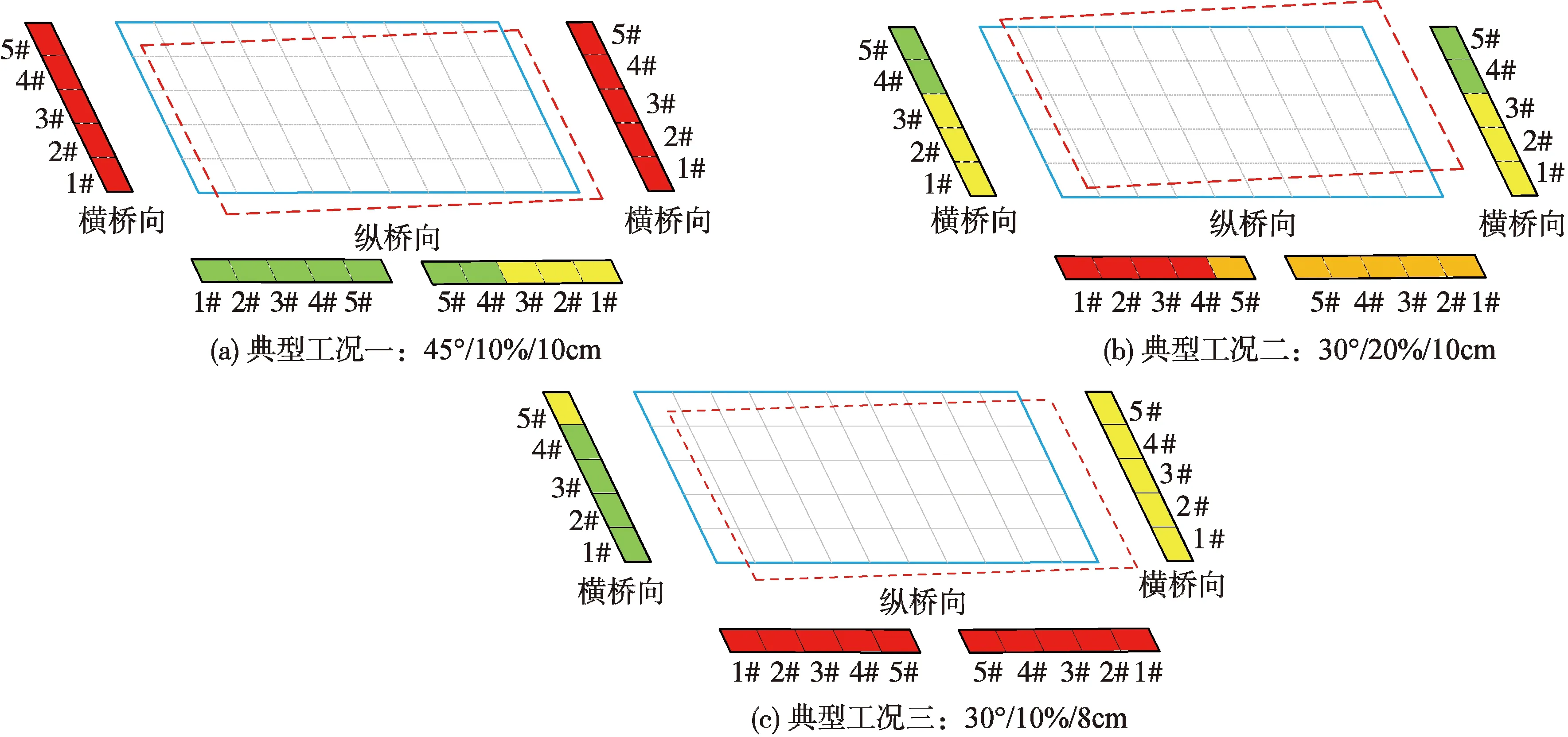
圖13 斜交簡支梁位移響應特征Fig.13 Displacement features of simply-supported skewed girder

4 結論

本文主要結論如下：

(1)斜交簡支梁橋的地震位移響應具有明顯的縱、橫向耦合特征，當斜交角小于30°時，位移響應以縱向為主，且在30°時達到最大值；當斜交角大于30°后，位移響應以橫向為主，且在60°時達到最大值。主梁平面轉角隨著斜交角的增大而先增后減，在斜交角為30°時達到最大值。

(2)擋塊不僅可有效制約支座的橫向位移，對支座縱向位移也有較好的約束效果，隨著擋塊強度的增大，支座縱、橫向位移以及主梁平面轉角均逐漸減小，但當擋塊強度達到某一數值時，其限位效果會逐漸趨于平緩，因此擋塊強度并非越大越好。本文橋例中，當擋塊強度達到30%恒載支反力時，其限位效果可達最優。

(3)斜交簡支梁橋在伸縮縫處存在不均勻碰撞現象，兩側角點處的碰撞力明顯更大，靠近橋面中心線處碰撞力最小甚至為0，不均勻碰撞使得斜交主梁容易沿著自身銳角端向橋面內發生轉動。

(4)本文橋例未出現落座情況，但出現大量嚴重滑動(即主梁與支座半脫空狀態)的工況，且隨著斜交角的增大，支座的滑動方向逐漸由縱向轉為橫向。伸縮縫大小對支座滑動影響很小，但適當增大擋塊的強度(尤其是適當加強斜交主梁銳角端的擋塊強度)可有效減輕支座的滑動狀態。