一種減小同步正交網(wǎng)網(wǎng)間干擾概率的跳頻表生成算法設(shè)計(jì)與驗(yàn)證

李紅衛(wèi)，林創(chuàng)勤，廖劍鏢

(1.廣東交通職業(yè)技術(shù)學(xué)院，廣東 廣州 510800；2.廣東省船舶自動(dòng)化工程技術(shù)研究中心，廣東 廣州 510800)

0 引 言

跳頻通信技術(shù)在現(xiàn)代通信中具有廣泛的應(yīng)用。跳頻組網(wǎng)是跳頻通信裝備發(fā)揮效能的重要途徑，目前國內(nèi)外對跳頻組網(wǎng)的研究主要集中于同步組網(wǎng)和異步組網(wǎng)技術(shù)等方面。所謂同步或者異步均是指跳頻網(wǎng)與網(wǎng)之間在射頻時(shí)序上的制約關(guān)系，不能將單獨(dú)的跳頻網(wǎng)歸結(jié)為同步組網(wǎng)或異步組網(wǎng)。

跳頻組網(wǎng)主要包括頻分組網(wǎng)和碼分組網(wǎng)兩大類：頻分組網(wǎng)與常規(guī)通信頻分組網(wǎng)類似，不同的跳頻網(wǎng)絡(luò)使用不同的跳頻頻率；碼分組網(wǎng)：所有跳頻網(wǎng)絡(luò)在相同的跳頻頻率表上跳頻，不同的跳頻網(wǎng)絡(luò)使用不同的跳頻圖案。根據(jù)跳頻圖案正交與否又分為正交跳頻網(wǎng)和非正交跳頻網(wǎng)。根據(jù)是否具有統(tǒng)一的時(shí)間基準(zhǔn)，跳頻組網(wǎng)可分為同步組網(wǎng)和異步組網(wǎng)。同步組網(wǎng)時(shí)，各跳頻網(wǎng)絡(luò)具有統(tǒng)一的時(shí)間基準(zhǔn)。異步組網(wǎng)時(shí)，各跳頻網(wǎng)絡(luò)沒有統(tǒng)一的時(shí)間基準(zhǔn)。正交跳頻網(wǎng)為了使跳頻圖案不發(fā)生重疊，要求全網(wǎng)做到嚴(yán)格定時(shí)，故一般采用同步組網(wǎng)方式。因此，從嚴(yán)格意義上講，正交跳頻網(wǎng)是同步正交跳頻網(wǎng)，一般簡稱為同步網(wǎng)。非正交跳頻網(wǎng)的跳頻圖案可能會(huì)發(fā)生重疊，因此可能會(huì)產(chǎn)生網(wǎng)間干擾。通過精心選擇跳頻圖案和采用異步組網(wǎng)方法，可以使網(wǎng)間干擾減小到最低限度。

1 跳頻組網(wǎng)參數(shù)

跳頻電臺(tái)工作的主要參數(shù)有：頻率集(FQR)、實(shí)時(shí)時(shí)鐘(TOD)、網(wǎng)絡(luò)時(shí)鐘(TON)、密鑰(KEY)、跳頻表、偽隨機(jī)序列發(fā)生器(PRG)。FQR：是由

N

個(gè)頻率組成的一個(gè)跳頻頻率集，記為{

f

,

f

,…,

f

}。TOD：代表跳頻同步所必需的偽碼發(fā)生器實(shí)時(shí)狀態(tài)。TON：Time of Net，跳頻系統(tǒng)的時(shí)間計(jì)數(shù)器，其單位為hop，其一般以網(wǎng)絡(luò)中某臺(tái)設(shè)備(如主臺(tái))的TOD為參照系。KEY：跳頻系統(tǒng)的信道密鑰，決定偽碼發(fā)生器的初始狀態(tài)。跳頻表：是

K

行

N

列的矩陣，

K

是組網(wǎng)的個(gè)數(shù)。同步正交組網(wǎng)的跳頻表滿足條件：(1)的每行是{

f

,

f

,…,

f

}的一個(gè)排列；(2)的每列互不相同。

2 網(wǎng)間干擾分析

跳頻偽隨機(jī)序列發(fā)生器PRG的計(jì)算與TON和KEY有關(guān)，假定KEY為函數(shù)

g

，

g

為正整數(shù)集到{1,2,…,

N

}的映射。

同步正交跳頻網(wǎng)要實(shí)現(xiàn)正常工作，須保證跳頻網(wǎng)的每一起跳時(shí)刻相同，并且任一頻率駐留時(shí)刻的各跳頻網(wǎng)瞬時(shí)射頻頻率正交，理論上同步網(wǎng)在維持同步時(shí)，無網(wǎng)間干擾現(xiàn)象。同步組網(wǎng)的技術(shù)難度也在于必須保證各個(gè)跳頻網(wǎng)間時(shí)鐘嚴(yán)格同步，技術(shù)難度大。但實(shí)際中由于跳頻技術(shù)體制裝備不可避免會(huì)發(fā)生時(shí)鐘漂移，且同步網(wǎng)各網(wǎng)之間的時(shí)鐘信息交換會(huì)增加同步信息內(nèi)容，同步時(shí)間增加，這些情況會(huì)導(dǎo)致網(wǎng)間干擾產(chǎn)生。

同步正交跳頻網(wǎng)的網(wǎng)間干擾主要有2種情況：延時(shí)干擾和TON不一致的干擾。

延時(shí)干擾示意圖如圖1所示，其中

f

()和

f

()分別表示網(wǎng)

i

和網(wǎng)

j

的跳頻表。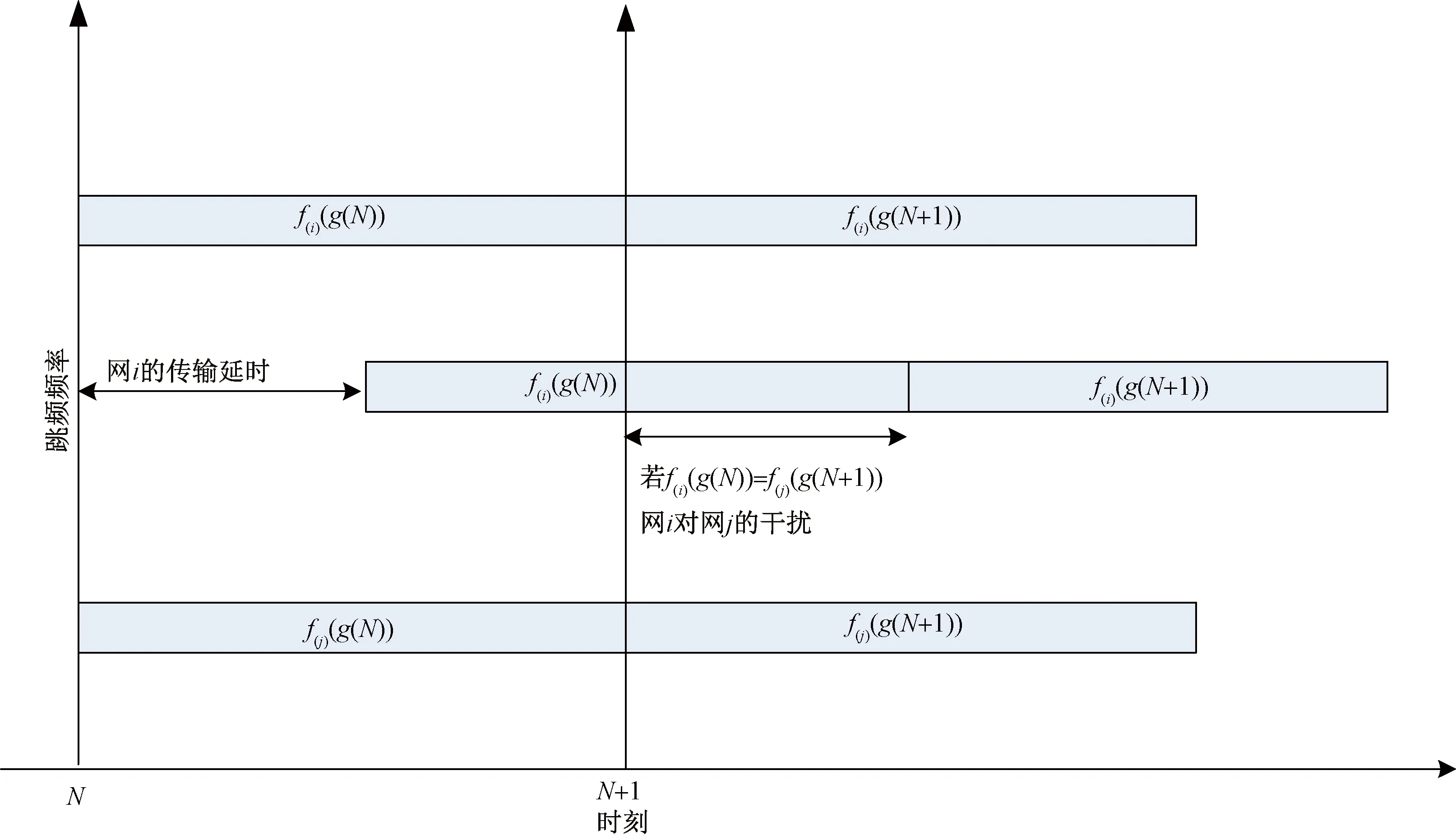

圖1 延時(shí)干擾示意圖

TON不一致干擾的示意圖如圖2所示。

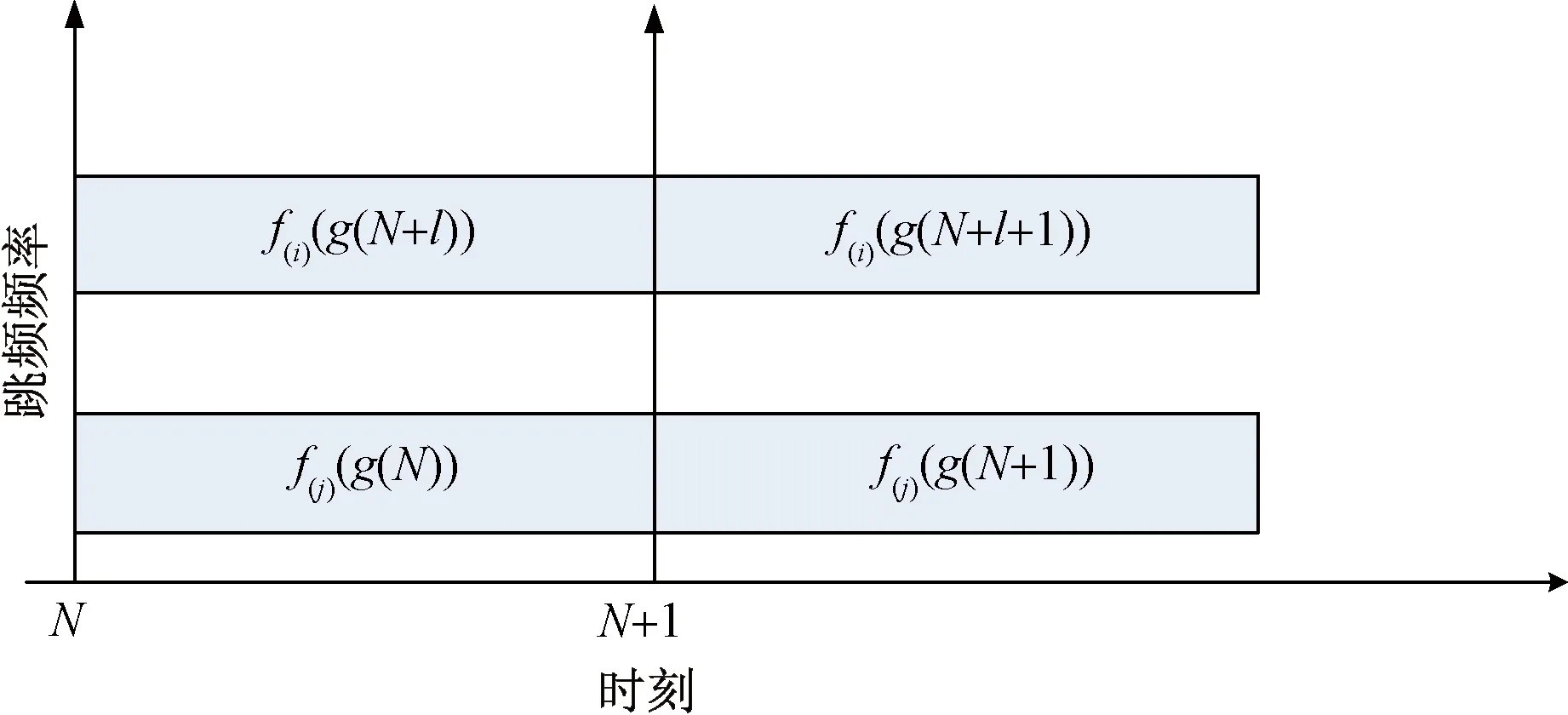
圖2 TON不一致干擾示意圖

若

f

()(

g

(

N

))=

f

()(

g

(

N

+

l

))，則在時(shí)刻

N

，網(wǎng)

i

對網(wǎng)

j

會(huì)產(chǎn)生干擾。

對于延時(shí)干擾，延時(shí)不是整數(shù)跳時(shí)性能一般優(yōu)于整數(shù)跳延時(shí)的性能，為了理論推導(dǎo)方便，只考慮延時(shí)為整數(shù)跳的情形，于是延時(shí)干擾亦可看作是TON不一致干擾。所以下文只考慮TON不一致干擾。

3 跳頻表生成算法設(shè)計(jì)

3.1 跳頻表交集矩陣與交集偏移量

本文定義給出跳頻表的交集矩陣的概念，它是分析網(wǎng)間干擾和指導(dǎo)跳頻表設(shè)計(jì)的一個(gè)重要量。

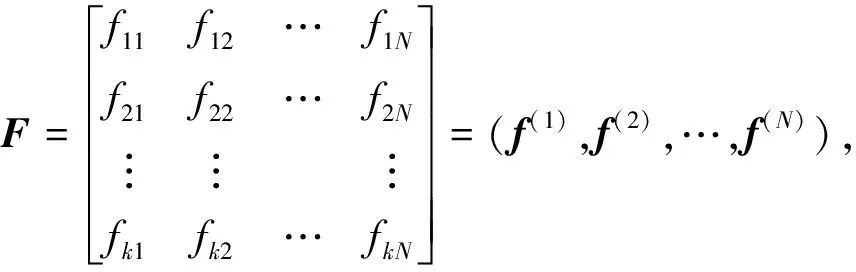
3.2 跳頻表交集偏移量最小準(zhǔn)則

(1) 網(wǎng)內(nèi)存在2種TON值理論分析

網(wǎng)內(nèi)的TON只有2個(gè)值，假設(shè)TON值為

K

和

K

，其中TON值為

K

的網(wǎng)有

k

個(gè)，TON值為

K

的網(wǎng)有

k

個(gè)，顯然

k

+

k

=

k

。不失一般性，只考慮TON值為

K

的網(wǎng)受到TON值為

K

的網(wǎng)的干擾。稱TON值為

K

的網(wǎng)為

K

-TON網(wǎng)。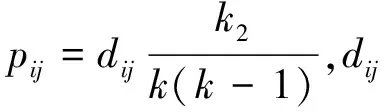

對于任何的跳頻表，上述結(jié)論都成立。

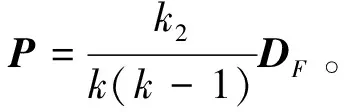
(2) 網(wǎng)內(nèi)存在3種TON值理論分析

網(wǎng)內(nèi)的TON只有3個(gè)值，假設(shè)TON值為

K

、

K

、

K

，其中TON值為

K

的網(wǎng)有

k

個(gè)，TON值為

K

的網(wǎng)有

k

個(gè)，TON值為

K

的網(wǎng)有

k

個(gè)，顯然

k

+

k

+

k

=

k

。不失一般性，只考慮TON值為

K

的網(wǎng)受到TON值為

K

的網(wǎng)和TON值為

K

的網(wǎng)的干擾。仍稱TON值為

K

的網(wǎng)為

K

-TON網(wǎng)。任何時(shí)刻，某個(gè)

K

-TON網(wǎng)可能受到

K

-TON網(wǎng)和

K

-TON網(wǎng)的干擾，從而存在一定的干擾概率。令

p

(

s

,

t

)表示

g

(

K

)=

i

,

g

(

K

)=

s

,

g

(

K

)=

t

情形下，一個(gè)

K

-TON網(wǎng)受到的

K

-TON網(wǎng)或

K

-TON網(wǎng)干擾的概率。下面來分析

p

(

j

,

k

)。

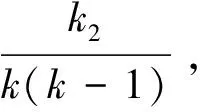
p

(

s

,

t

)=1-(1-

p

)(1-

p

)=

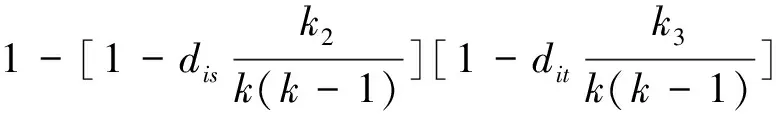
(1)

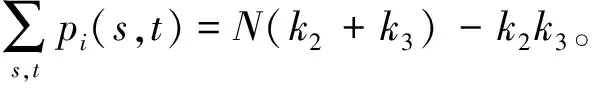
對于任何跳頻表，上述結(jié)論都成立。

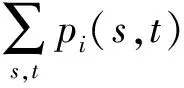
3.3 算法設(shè)計(jì)

由第3.2節(jié)可以看出，網(wǎng)內(nèi)有2種或3種TON值時(shí)，均希望

σ

最小。所以設(shè)計(jì)跳頻表的準(zhǔn)則是使得交集偏移量

σ

最小。依據(jù)上述準(zhǔn)則，可以利用如下算法通過計(jì)算機(jī)搜索較好的跳頻表。跳頻表的生成算法：

(2) 把的列進(jìn)行隨機(jī)置換，得方陣，再對的行進(jìn)行隨機(jī)置換，得方陣，并令為的前

k

行。(3) 計(jì)算

σ

，若

σ

<

σ

，則更新

σ

=

σ

，并更新=。返回(2)，直到循環(huán)次數(shù)到達(dá)上限。(4) 輸出。

4 跳頻表網(wǎng)間干擾概率驗(yàn)證

以

N

=16，

k

=10為例，進(jìn)行10 000次搜尋的

σ

(按照與均值差的絕對值和計(jì)算)值的仿真圖如圖3所示。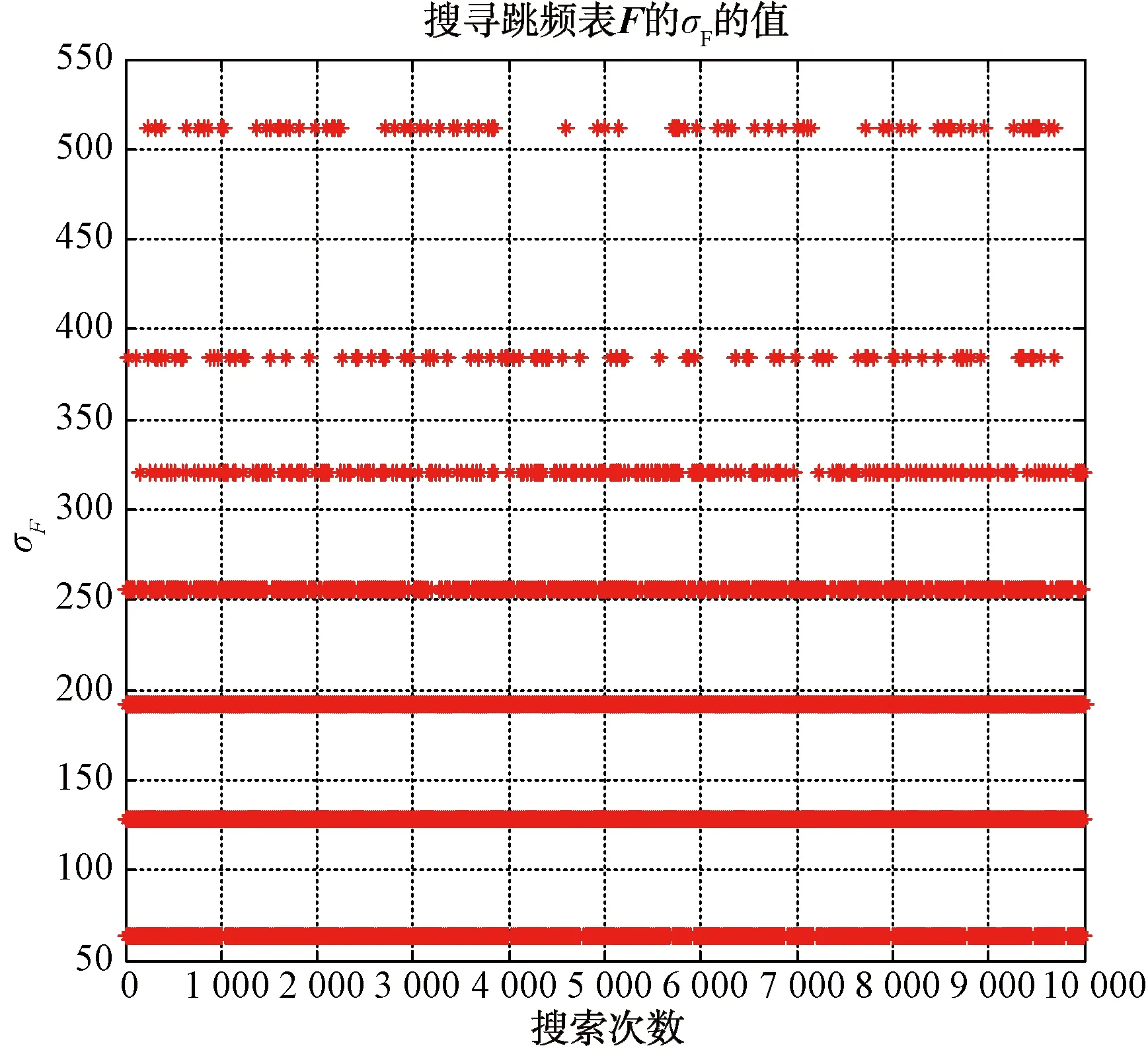

圖3 10 000次搜尋F的σF值仿真圖

從仿真結(jié)果可知，只需要在最小

σ

對應(yīng)的跳頻表中找一個(gè)作為跳頻表即可。以

N

=16，

k

=10為例，本例不經(jīng)過優(yōu)選，對采用如下常用跳頻表的干擾概率進(jìn)行分析。

其交集矩陣為：

由此可見，交集矩陣的分布很不均勻，可想而知性能不好。交集偏移量

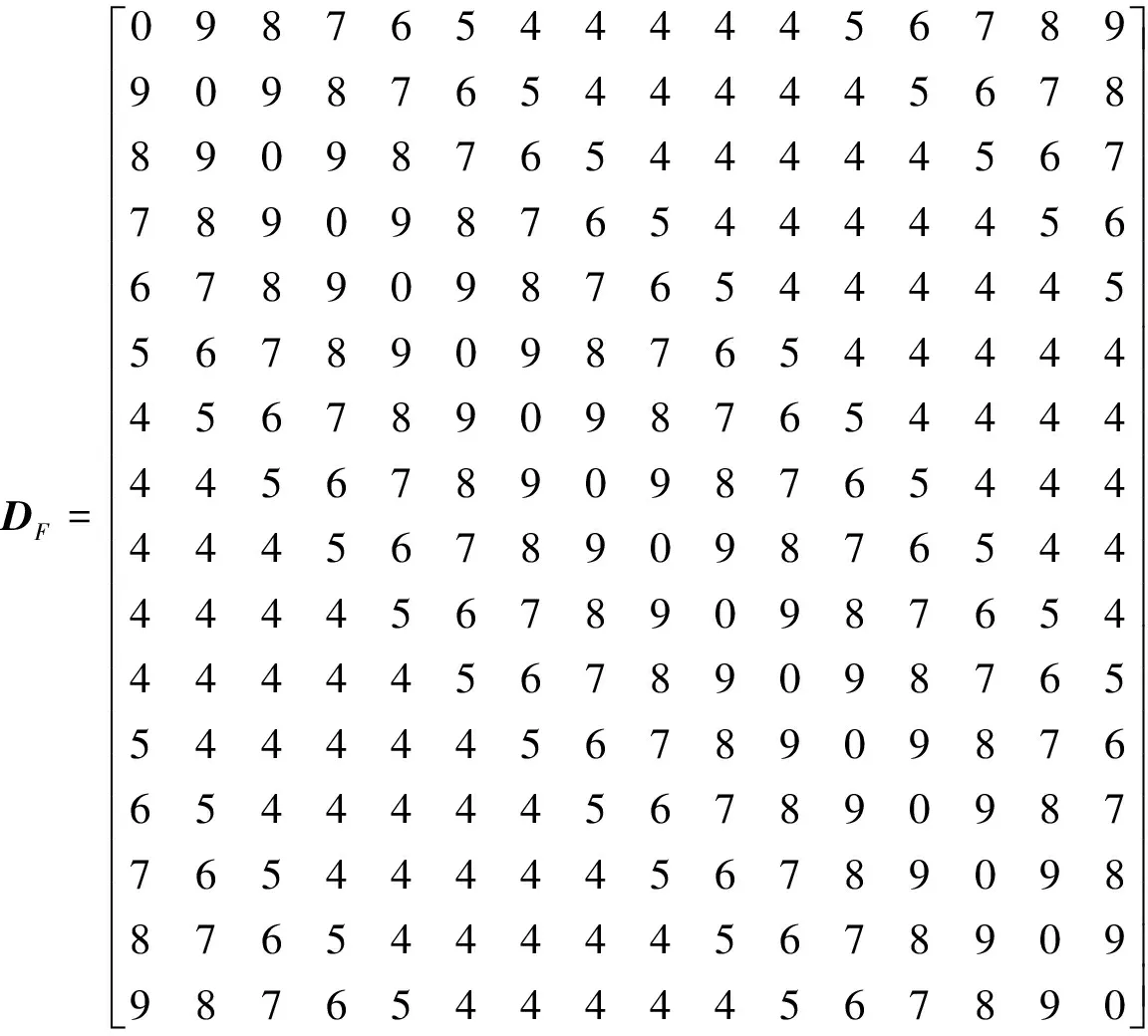
σ

為384，要遠(yuǎn)大于經(jīng)過優(yōu)選后

σ

的值。

以下是上述情況下幾種不同情形的干擾概率的計(jì)算：

(1) 情形1:網(wǎng)絡(luò)中有2個(gè)TON值，且

k

=1,

k

=9。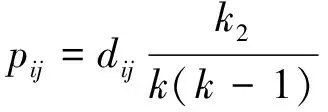

可以看出，

N

=16,

k

=10,

k

=1,

k

=9時(shí)，

K

-TON網(wǎng)的干擾概率為從0～0.9不等，而且如果密鑰函數(shù)使得

g

(

K

)=

i

,

g

(

K

)=

i

+1或

g

(

K

)=

i

,

g

(

K

)=

i

-1時(shí)，

K

-TON網(wǎng)被干擾的概率高達(dá)0.9，這是不希望的。(2) 情形2：網(wǎng)絡(luò)中有2個(gè)TON值，且

k

=2,

k

=8。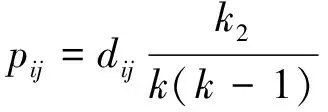

可以看出，

N

=16,

k

=10,

k

=2,

k

=8時(shí)，

K

-TON網(wǎng)的干擾概率為從0～0.8不等，而且如果密鑰函數(shù)使得

g

(

K

)=

i

,

g

(

K

)=

i

+1或

g

(

K

)=

i

,

g

(

K

)=

i

-1時(shí)，

K

-TON網(wǎng)被干擾的概率高達(dá)0.8，這是不希望的。(3) 情形3：網(wǎng)絡(luò)中有3個(gè)TON值，且

k

=1,

k

=1,

k

=7。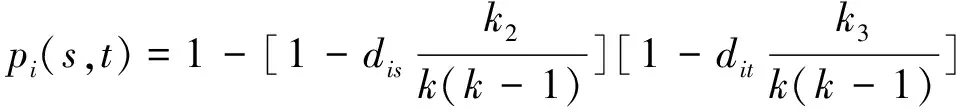

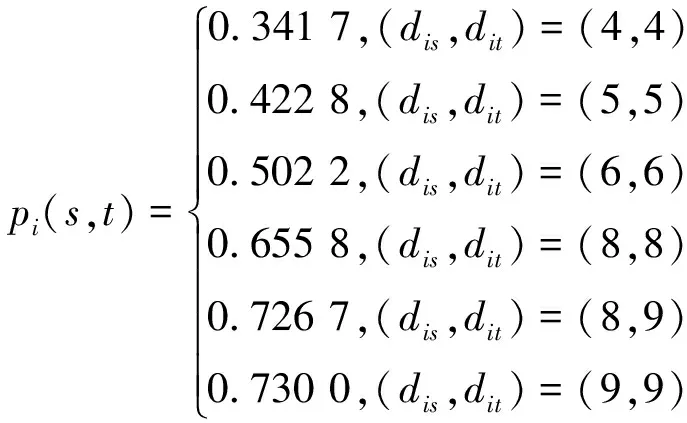
可見

p

(

s

,

t

)隨著密鑰函數(shù)

g

的變化，被干擾的概率變化是劇烈的，惡劣的情形下，密鑰函數(shù)

g

可能導(dǎo)致

K

-TON網(wǎng)被干擾的概率為0.73。(4) 情形4：網(wǎng)絡(luò)中有3個(gè)TON值，且

k

=1,

k

=2,

k

=6。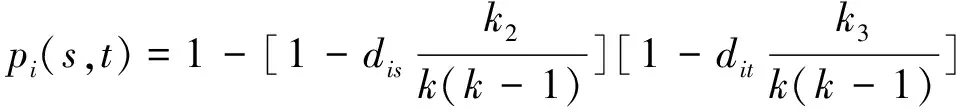

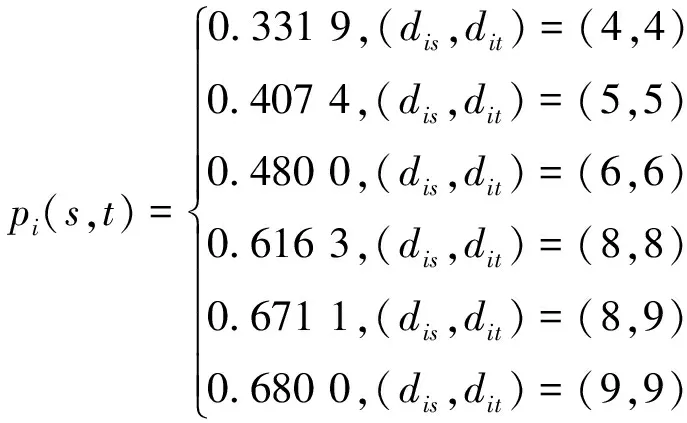
可見

p

(

s

,

t

)隨著密鑰函數(shù)

g

的變化，被干擾的概率變化是劇烈的，惡劣的情形下，密鑰函數(shù)

g

可能導(dǎo)致

K

-TON網(wǎng)被干擾的概率為0.68。

5 結(jié)束語

本文分析了同步正交跳頻網(wǎng)的網(wǎng)間干擾類型，針對TON不一致干擾從實(shí)際使用中存在2種和3種TON值進(jìn)行理論分析，驗(yàn)證了所設(shè)計(jì)的跳頻表交集偏移量最小準(zhǔn)則的有效性，依據(jù)該準(zhǔn)則設(shè)計(jì)了跳頻表的生成算法，從跳頻表網(wǎng)間干擾概率驗(yàn)證結(jié)果可以看出，以交集偏移量

σ

最小準(zhǔn)則為指導(dǎo)，經(jīng)過優(yōu)選設(shè)計(jì)的跳頻表的性能優(yōu)于常用的跳頻表的性能，而且基本上已經(jīng)達(dá)到了最優(yōu)(達(dá)到最優(yōu)的條件是交集矩陣的分布是完全均勻的，均值跳頻表的設(shè)計(jì)無關(guān)的定值)，充分說明本算法的有效性。