基于粒子群優化的列車制動曲線分段方法研究
鮑鵬宇,陳志強,王建敏,于曉娜,張友兵,張貴娟
(1.北京全路通信信號研究設計院集團有限公司,北京 100070;2.北京市高速鐵路運行控制系統工程技術研究中心,北京 100070)
1 概述
列車運行控制系統是保障列車安全運行,提高運輸效率的重要裝備[1],由車載設備和地面設備組成。列車自動防護系統(Automatic Train Protection, ATP)是列控系統的車載設備,其根據地面設備提供的線路數據、臨時限速等信息,生成列車速度和距離控制模式曲線,使列車在模式曲線監控下安全運行[2]。
緊急制動減速曲線(Emergency Brake Deceleration, EBD)和常用制動減 速曲線(Service Brake Deceleration, SBD)是列車制動模式曲線的基本元素,二者均由列車固有減速性能即制動減速度確定[3-5]。為提高制動曲線的運算效率,車載系統計算列車制動減速度曲線時,通常對列車制動速度-減速度曲線進行分段近似處理,將減速度分為3~6段。在相同的速度分段內,使用最低的減速度進行近似描述真實減速性能[6]。由于不同類型的列車制動曲線差別較大,沒有統一的減速度分段方法,如何進行列車制動減速度分段,使得制動模式曲線具有最佳性能是列控車載系統的一個難題。
針對此問題,本文提出了基于粒子群優化(Particle Swarm optimization, PSO)的列車制動速度-減速度曲線分段方法。通過構建制動距離目標函數,對分段參數進行優化,從而獲取最優的分段參數,使得制動距離最短,并通過仿真對分段方法的性能進行了驗證。
2 列車制動模式曲線優化目標
制動距離是描述列車制動模式曲線最優性的關鍵目標。在制動計算中,通常可以將制動距離簡化為空走制動距離和有效制動距離之和,決定空走制動距離的兩個因素是制動初速度和空走時間[6]。由于空走時間僅與列車制動性能相關,不受制動分段的影響,因此相同制動初速度下的制動距離是評價制動模式曲線性能的關鍵指標。
設列車制動減速度曲線可分為N段,每段的制動減速度和最高速度分別為an和vn,0<n≤N。通過反向計算可得到列車的最大制動距離dmax:

其中,v0=0,vN=vmax,vmax為列車允許運行的最大速度。由于列車制動減速度a是速度v的函數。因此第n段的最小減速度an為:
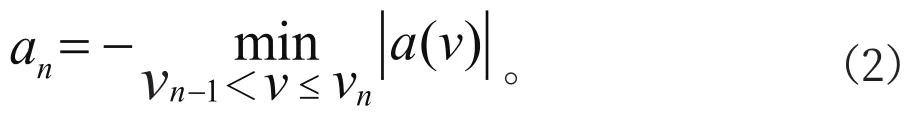
3 制動模式曲線分段粒子群優化模型
粒子群算法是通過模擬鳥群覓食行為而發展起來的一種基于群體協作的隨機搜索算法[7]。假設待優化的參數可組成D維空間,空間中分布有若干個粒子。每個粒子對應著目標函數的一個解,在D維空間中以一定的矢量速度搜索目標函數的最優解。
設N段的制動曲線分段參數可組成N-1維空間,空間中分布有M個參數粒子,第m個粒子的位置xm和速度vm可分別表示為:
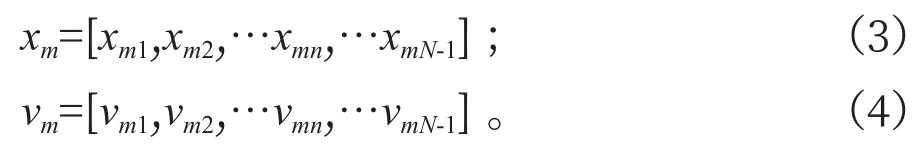
其中,0<n<N,0<m≤M,xmn表示第m個粒子的第n個速度分段點;vmn表示第m個粒子的第n個速度分段點的移動速度。
每個粒子均具有記憶功能,在移動的過程中能根據經驗判斷自身經歷的最優位置pbestm,并通過種群交流得到群體最優位置gbest。每個粒子通過不斷的向pbestm和gbest學習,更新自身位置以使得自身位置趨于最優解。位置xm和速度vm更新方法如下[8-9]:

其中,t為當前的迭代次數,vmn(t+1)和xmn(t+1)為第m個粒子在第t次迭代中第n維的速度和位置,ω為粒子的慣性權重,φ1和φ2為學習因子,r1(t)和r2(t)為[0,1]之間均勻分布的隨機因子,r1(t)和r2(t)在每次迭代中均有變化,可保證粒子群中個體的多樣性。
由此建立了以列車制動曲線分段點為粒子群參數,以最優制動距離MIN(dmax)為目標函數的列車制動模式曲線分段粒子群優化模型。
4 仿真分析
以長客16輛編組CR400BF型動車組(簡稱CR400BF)為例,對基于粒子群優化的制動曲線分段方法性能進行分析。如圖1(a)所示,CR400BF的含風阻濕軌緊急制動速度-減速度曲線為非單調曲線。隨著車速的變化,制動減速度呈現先增加,后減小的變化特點,變化率也不斷變化。
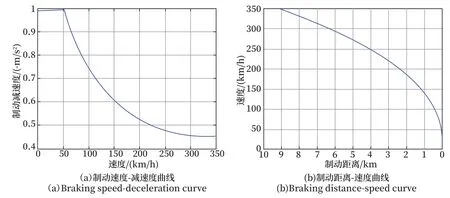
圖1 長客16輛編組中國標準動車組制動參數及曲線Fig.1 Chinese standard EMU with 16 cars manufactured by Changchun Railway Vehicles Co
將CR400BF精細制動速度-減速度數據代入公式(1)中,可得到不同速度下的列車制動距離如圖1(b)所示。其中,列車的最大制動距離,即車速從 350 km/h 降到 0 km/h 的制動距離為 9 096.5 m。
根據前面的分析,精細化的制動模型雖然可得到最短的制動距離,但運算效率低。因此,本文以6段的制動減速度分段為例,對基于粒子群優化算法的制動減速度模型有效性進行驗證。
設優化目標為公式(1)所描述的制動距離dmax最小化。粒子群共有200個粒子,其參數為分段點速度,慣性權重ω為0.728 94,學習因子φ1和φ2為1.496 18。經過粒子群優化算法的200次迭代,可得到近似最優的6段制動減速度如圖2(a)所示,制動距離與速度的關系如圖2(b)所示。其中,列車的最大制動距離,即車速從350 km/h降到0 km/h的制動距離為9 454.5 m,與精細化分段距離的近似絕對誤差為358 m,相對誤差為3.9%。
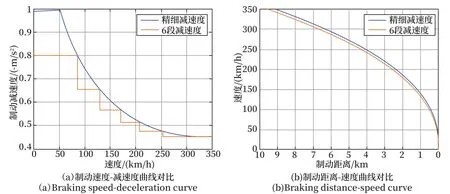
圖2 粒子群優化6段制動減速度對比Fig.2 Comparison of deceleration with 6 braking segments based on particle swarm optimization
5 結論
本論文以粒子群優化算法為基礎,對列車制動曲線分段方法進行了研究,通過將制動分段點為優化參數,以制動距離為優化目標的方法,實現了列車制動曲線的任意段最優近似,為列車制動曲線分段點的選取提供了一種快速的近似最優解決方案。基于本論文的研究方法,具有收斂速度快、條件依賴少的特點,可實現任意車型、任意減速度曲線、任意段數的列車制動曲線最優分段,具有很好的應用價值。

