利用雙極性天線探測及削弱多路徑效應的方法
張艷紅 張 鵬 赫雲輝
(1. 廣州市城市規劃勘測設計研究院, 廣東 廣州 573199; 2. 精密工程與工業測量國家測繪地理信息局重點實驗室, 湖北 武漢 430079; 3. 北京中色地科測繪有限公司, 北京 101300)
0 引言
本文主要從雙極性天線、基于載噪比的多路徑探測、多路徑削弱技術與實測數據分析四個部分展開研究。首先介紹了全球定位系統(Global Positioning System,GPS)信號的極化特性,詳細說明了雙極性天線的構成,并且分析了雙極性天線接收信號的情況;其次,對于基于載噪比的多路徑探測有一個較為清晰的認識,為后續的實測數據分析提供理論依據;然后,對于多路徑效應的削弱技術做了簡要說明;最后,應用雙極性天線和ublox公司的芯片組成簡單的GPS接收機,獲取實測數據。利用開源程序包(RTKLIB)對實測數據進行數據后處理,對比剔除衛星前后的固定率。
1 雙極性天線
信號的極化特性是在信號幅值、相位、頻率和波形等信息之外,另一可資利用的重要特征。衛星信號采用右螺旋圓極化(Right Hand Circular Polarization,RHCP)方式進行傳播,而經過一次反射后衛星信號就會變為左螺旋圓極化(Left Spiral Circular Polarization,LHCP),因此,可以通過分析衛星信號的極化特性來判別該信號是否經歷了多路徑效應[1]。雙極性天線由兩個相位中心相同的 RHCP 天線和 LHCP天線構成,RHCP天線主要用于接收直射衛星信號,LHCP天線則被設計用來接收反射信號。對于同一顆衛星,如果 LHCP 天線輸出的衛星信號強度始終維持在較低的級別,那么可以判斷接收到的衛星信號中不包含明顯的反射信號;而如果 LHCP 輸出衛星信號的信號強度較高,那么該衛星信號就有很大的概率經歷了嚴重的多路徑效應[6]。
理想情況下 RHCP天線會接收 RHCP 信號,而完全衰減掉 LHCP 信號。但是由于制造工藝的限制,RHCP 天線也會輸出LHCP 信號,只是RHCP 天線對RHCP 信號的增益遠遠大于對LHCP信號的增益。同理,LHCP天線對LHCP信號的增益也會遠遠大于對RHCP信號的增益[2]。
2 基于載噪比的多路徑探測
2.1 載噪比簡介
接收信號相對于噪聲的強弱程度,即信號的質量,可以用信噪比(SNR)來表示,它是信號功率PR與噪聲功率N之間的比率[3],即
(1)
式中,RSN并沒有相應的單位,經常采用分貝(dB)的形式來表示。因為噪聲帶寬B的取值影響著噪聲功率N和信噪比RSN的大小,所以需要帶寬值B的步驟會給信噪比的應用帶來不便,于是提出了載波噪聲比C/N0,簡稱載噪比,它的定義如式(2)所示:
(2)
式中,T為噪聲溫度;k為玻耳茲曼常數;噪聲功率N則等價于相應的兩者與對應噪聲帶寬B的乘積;N的單位為瓦特(W),T的單位為開爾文(K),則載噪比的單位為Hz(或dB·Hz)。
2.2 多路徑探測
前面介紹了載噪比可以作為接收信號質量的一個衡量標準,在使用雙極性天線時,LHCP天線輸出的載噪比則可以衡量多路徑效應,RHCP天線輸出的載噪比可以代表直射信號的強度。RHCP天線輸出的載噪比值偏低,即是信號比較弱,載噪比值偏高,即是信號比較強,質量比較好。在多路徑效應的影響下,LHCP天線輸出的載噪比會提升。因此,可以通過兩者載噪比的差值來衡量環境中多路徑影響的大小,其中,規定載噪比的差值為RHCP載噪比值減去LHCP載噪比值[4-6]。理論上,在多路徑較溫和的環境中,RHCP輸出的載噪比大,LHCP輸出的載噪比小,載噪比差值會較大;在多路徑較惡劣的環境中,LHCP載噪比大,載噪比差值會較小。
3 多路徑削弱技術
下面主要介紹基于載噪比削弱多路徑效應的相關技術。根據2.2節的相關介紹,左右旋天線的載噪比差值可以判定該位置受到的多路徑效應的大小,差值越大受多路徑的影響越小,差值越小受多路徑的影響就越大[12-13]。因此,最簡單的削弱方法則是在觀測衛星數量足夠多時,利用觀測值的載噪比信息,對各個衛星進行定權,受多路徑影響較大的觀測值合理的降權,受多路徑影響較小的觀測值合理地提高權值[9-11]。
對于單點定位,偽距觀測的觀測方程的實用形式如下:
cVtR+cVts-(Vion)i-(Vtrop)i
(3)
式中,(Xi,Yi,Zi)為第i顆衛星的三維坐標;(X,Y,Z)為測站的三維坐標;c為光速;VtR為接收機鐘差;Vts為衛星鐘差;(Vion)i為電離層誤差;(Vtrop)i為對流層誤差。在組建誤差方程時,使用測站的近似坐標(X0,Y0,Z0)Vts,一般未知數為測站的三維坐標(Xi,Yi,Zi)以及接收機鐘差Vts,依據經典平差理論可以得到
v=Ax-l
(4)
(5)
則可解得:
(6)
(7)
式中,P為觀測值的權陣,一般情況下觀測值精度相同則為單位陣,那么根據雙極性天線輸出的載噪比信息,并由此得出權重矩陣
(8)
求得X(1)后,再以X(1)為近似值繼續迭代,直到前后兩次的VTPV值相等,迭代終止,迭代的公式可以表達為:
(9)
(VTPV)(k)=(VTPV)(k+1)
(10)
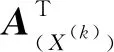
(11)
式中,n-t為模型的自由度,根據誤差傳播定律可以得到未知數的協因數矩陣
QXX=(ATPA)-1
(12)
對于單天線而言,載噪比信息包含內容較為豐富,利用載噪比定權也能一定程度地減少信號質量較差的衛星觀測值在解算中的使用,但這一指標與載波信號噪聲相關。在使用雙極性天線后,我們可以得到RHCP天線的載噪比輸出值,同時獲取LHCP天線的載噪比輸出值,前面介紹了載噪比差值與多路徑效應之間的關系,多路徑信號較強的情況下,載噪比的差值比較小,相反,多路徑信號較弱的情形下,載噪比差值則比較大。在探測出存在多路徑影響的衛星后,可以對該衛星的觀測值進行降權處理[7-8]。
以上是比較成熟的基于雙極性天線左右旋載噪比輸出值的削弱多路徑效應的理論方法。基于此,我們提出了應用RTKLIB軟件剔除左旋載噪比輸出值較大的衛星,即剔除受多路徑影響嚴重的衛星觀測值,使其不參與基線解算來削弱多路徑效應對解算結果的影響。
4 實測數據分析
4.1 試驗場景描述
本節試驗的地點位于武漢大學測繪學院樓頂,圖1(a)為架設在測繪學院樓頂西側的基準站,圖1(b)為同在測繪學院樓頂東側的移動站,兩者相距100 m之內。在基準站和移動站處選用的是雙極性天線包含RHCP和LHCP兩路輸出。可以處理的頻率范圍包含了GPS的L1頻段,能夠滿足本次試驗的要求。圖1(c)為雙極性天線的圖片。

圖1 試驗測站及雙極性天線
4.2 試驗過程
圖2為基準站和移動站的試驗流程,如圖2所示,在基準站位置采用ublox-NEO-M8P-2模塊(圖中簡稱為P)連接雙極性天線的右旋輸出,播發RTCM格式數據。同時,采用ublox-NEO-M8T-0(圖中簡稱為T)模塊連接雙極性天線的左旋輸出,接受原始測量值,為數據后處理時提取載噪比提供數據源。同理,在移動站位置采用ublox-NEO-M8P-2模塊連接雙極性天線的右旋輸出,接收原始觀測值。同時,采用ublox-NEO-M8T-0模塊連接雙極性天線的左旋輸出,接收原始測量值。
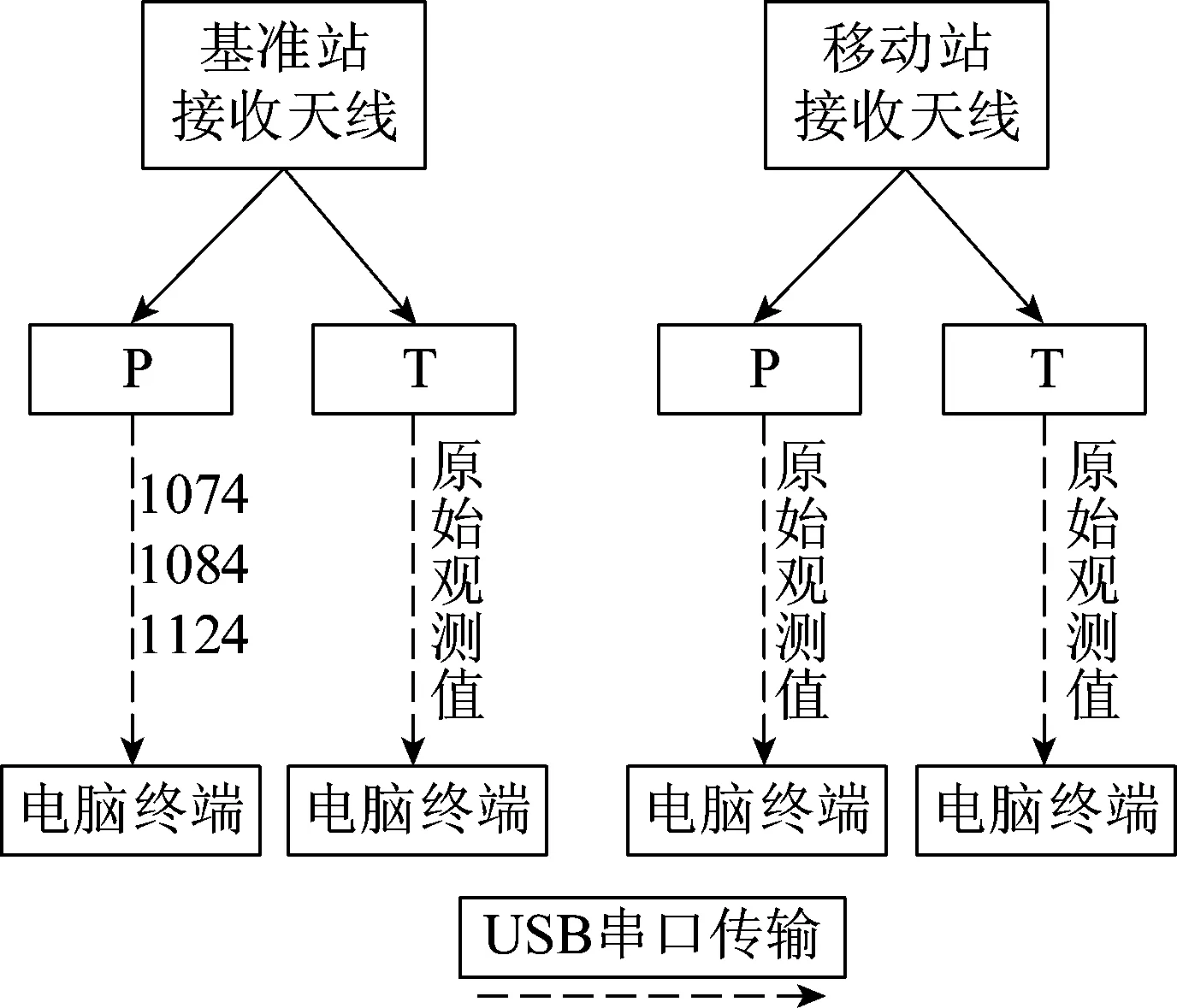
圖2 試驗流程
4.3 數據分析
本文中的試驗數據均使用RTKLIB軟件進行數據后處理。首先,利用RTKLIB軟件中的數據轉換模塊(RTKCONV)將接收到的所有數據轉換為觀測值文件類型;然后,利用數據處理模塊(RTKPOST)進行基線解算;最后,利用圖形繪制模塊(RTKPLOT)顯示基線解算的結果。
為了描述方便,23號衛星簡稱為G23。由于G23高度角較低,且與教學實驗大樓的位置具備產生多路徑效應的幾何結構,因此我們認為雙極性天線接收到的G23的觀測值受到多路徑的影響較為嚴重。因此,在數據后處理的過程中重點關注剔除G23觀測值前后基線解算結果的固定率情況。如果剔除G23觀測值之后的基線解算結果的固定率較剔除G23觀測值之前基線解算結果的固定率有明顯提高,則說明G23的觀測值受到嚴重的多路徑效應影響。下面將圍繞剔除G23前后解算結果的固定率、標準差(STD)和均方根誤差(RMS)展開詳細說明。
整周模糊度解算是否正確直接影響RTK定位的精度。而模糊度固定的性能可以通過模糊度固定率來體現,模糊度固定率可以表示為:
(12)
式中,NCF表示固定的歷元個數;NT表示解算的整個歷元總數。
利用RTKPOST對兩個ublox-NEO-M8P-2模塊接收的測量值數據進行基線解算。剔除G23觀測值前后解算結果如表1所示。剔除G23觀測值之前固定率為5.2%,剔除G23觀測值之后固定率為45.7%。

表1 剔除G23前后固定率
用RTKLIB對獲得的原始觀測值數據進行基線解算,如表1所示,剔除G23之前解算結果的固定率為5.2%,剔除G23之后解算結果的固定率有顯著提高,可以達到45.7%。說明剔除G23后,原始觀測值的質量有所提高,因而最終解算結果的固定率會有顯著的提高。
在觀測時段內,定位結果的位置偏差在一定意義上可以反映出定位結果的好壞,在只有固定解的情況下,剔除G23觀測值前后的STD和RMS詳細對比如表2所示,剔除G23觀測值后,解算結果的STD和RMS都有較大的提高。

表2 剔除G23前后標準差(STD)和均方根誤差(RMS) 單位:m
分析固定率提高時間段內基準站左旋輸出的載噪比值,如圖3所示,此時段內的左旋載噪比輸出量較大,基于上述雙極性天線的理論描述,認為此時間段內此衛星的觀測值受到嚴重的多路徑效應的影響。因此,采用剔除此衛星,使其不參與基線解算的方式,降低多路徑效應對基線解算結果的影響。
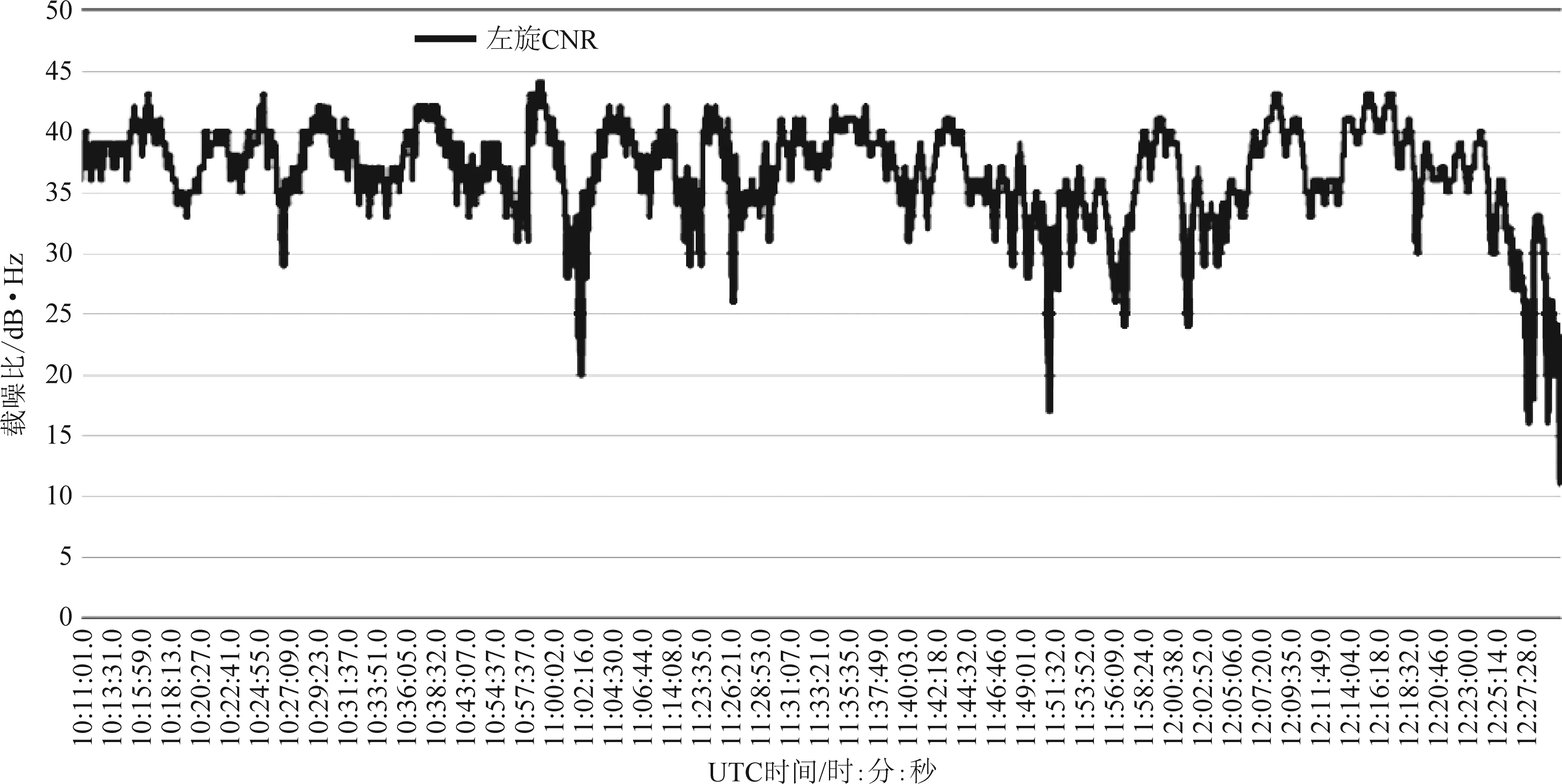
圖3 G23在基準站處的載噪比
同理,同時間段內移動站處剔除G23觀測值前后左旋輸出的載噪比的值如圖4所示。由圖4可知,移動站處左旋輸出的載噪比也較高,部分區域能夠達到40 dB·Hz,故認為移動站此時段內同樣存在明顯的多路徑現象。
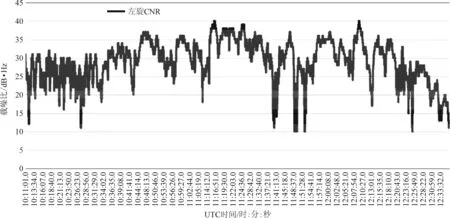
圖4 G23在移動站處的載噪比
5 結束語
本文主要的思路是首先做常規的基線解算,根據此時段中天空圖中衛星的運動軌跡,分析此時段衛星是否與移動站周圍的高大建筑物(教學實驗大樓),形成具有多路徑效應的幾何關系。如若幾何關系成立,則分析此時間段內該衛星左右旋載噪比輸出量值的大小。若此時段內該衛星左旋載噪比輸出值較大,則說明存在嚴重的多路徑效應,則剔除該衛星,使其不參與基線解算。將剔除該衛星前后的基線解算結果進行對比。若基線解算結果的固定率有顯著提高,則說明在一定程度上該衛星的多路徑效應得到了明顯的削弱。

