網絡化遙操作系統的全狀態時變約束控制研究
楊亞娜,代 特
(燕山大學 電氣工程學院,河北 秦皇島 066004)
0 引言
典型網絡化遙操作系統主要由操作者、主機器人、網絡信息傳輸通道、從機器人和從端的外界工作環境五部分組成[1]。其工作模式可大致描述為:操作者操作主機器人,并將主機器人的位置、速度等信息通過網絡等傳輸媒介傳輸給遠端從機器人,從機器人根據接收到的主機器人信號在特定環境下模擬主機器人的行為來配合操作者完成各項工作。同時,從機器人將自己的位置、速度、力等信息通過網絡傳輸通道反饋給操作者,便于操作者根據從機器人的運動狀態做出正確的決策[2-3]。遙操作系統作為能最大限度發揮人類和機械系統各自優勢的遠程操作系統,目前已被廣泛應用于核事故救援、空間探測、海底作業和遠程醫療以及農業等多個領域[4-7]。
隨著遙操作系統使用范圍的不斷擴大,對遙操作系統控制性能的要求日益提高。遙操作系統控制器的設計需同時滿足多種性能需求:1)通信時延下閉環遙操作系統的穩定性;2)良好的主-從機器人同步精度;3)較快的系統瞬態響應速度等。由于主-從機器人之間通過網絡相連,因此不可避免地存在通信時延問題[8]。另外,遙操作系統作為典型的非線性系統,在實際中存在不同程度的模型未知、參數不確定以及未知外界干擾等問題。遙操作系統在實際工作中,由于工作環境的限制、操作的安全性以及性能提高的考慮,系統狀態往往受到不同程度的約束。正是因為主-從通信時延、系統不確定性和系統狀態約束的存在,迫切需要針對網絡化遙操作系統設計全狀態約束控制策略以保證主-從系統高精、快速同步的基礎上,保證系統狀態始終處于所約束范圍以內。
近年來,針對單機器人以及非線性系統的狀態約束控制問題,現有文獻進行了深入的研究。許多有效的控制設計方法,包括模型預測,參考調節器和函數集合不變性概念被提出。除此之外,基于障礙Lyapunov方程(Barrier Lyapunov Function, BLF)的控制器設計方法取得了大量的研究成果。該方法通過設計新的帶有約束的Lyapunov方程,并設計有效的控制器,使得Lyapunov方程始終有界,即所選取的約束函數有界,從而確保受限狀態始終處于約束范圍以內[9]。基于該方法,文獻[10]針對嚴格反饋非線性系統提出了一種針對輸出約束的控制器設計方法,通過選取對稱時變BLF來確保系統輸出滿足約束條件。進而文獻[11]針對一類非線性系統考慮系統的部分狀態約束問題,提出了一種新的基于BLF的控制方案。文獻[12]針對一類具有輸入飽和、狀態約束、匹配參數不確定性和輸入擾動的多輸入多輸出系統,提出了一種雙環控制方法。文獻[13]針對一類具有全狀態約束的非線性純反饋系統設計了自適應控制方案。然而,在上述文獻中,大多只考慮系統的輸出約束或者帶有恒定約束條件的狀態約束問題。然而,由于實際工作環境的復雜多變以及控制目標的時變性,非對稱時變狀態約束問題更具實際研究意義。另外,雖然現有針對非線性系統狀態約束問題取得了一定的研究成果,但上述控制方法很難直接應用于帶有信號傳輸時延的網絡化遙操作系統。
在遙操作系統的實際應用中,主-從機器人之間的通信傳輸時延特別是時變的傳輸時延,給控制器設計帶了巨大的挑戰[14-17]。文獻[18]針對帶有定常時延的遙操作系統,考慮機器人位置約束問題,設計自適應控制器,保證了主從機器人的快速同步性能。進而,文獻[19]針對帶有定常時延、輸入飽和、多狀態約束下的雙邊遙操作系統的同步控制問題進行了深入研究,通過設計神經網絡控制策略保證了閉環遙操作系統的穩定性。然而,實際中主-從端通信時延大多具有非對稱時變特性。
針對以上存在的問題,本文擬針對帶有非對稱時變約束、系統不確定、未知外界干擾的網絡化遙操作系統在多狀態約束下的控制問題展開研究,通過設計新的自適應神經網絡控制策略,保證閉環遙操作系統穩定的同時,使得系統狀態始終處于受限的范圍以內。本文的主要貢獻點可歸納如下:
1) 針對帶有模型和參數不確定的網絡化遙操作系統在時變非對稱全狀態約束下的同步控制問題,通過設計新的自適應控制策略保證系統具有良好的暫穩態性能。
2) 針對主-從機器人之間存在的不對稱時變通信時延,本文創新性地利用非線性觀測器在線估計并補償時延的影響,從而避免控制器的設計依賴于時延導數信息,在提高系統跟蹤精度的基礎上,增強了控制器的實用性。
3) 徑向基神經網絡(Radial Basis Function Neural Networks,RBFNN)與障礙Lyapunov函數的結合放松了神經網絡控制中要求輸入信號均保持在一個緊集合這一假設條件,且通過設計簡化的調整機制,減少計算量,縮短神經網絡計算時間。
4) 利用Nussbaum增益,很好地處理了不確定輸入矩陣對系統穩定性的影響,實現更高精度的同步控制。
1 預備知識
1.1 遙操作系統模型描述
考慮兩個具有n-關節機械臂組成的主-從非線性遙操作系統動力學模型:

(1)
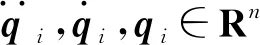
上述非線性主-從機器人系統存在如下重要屬性:
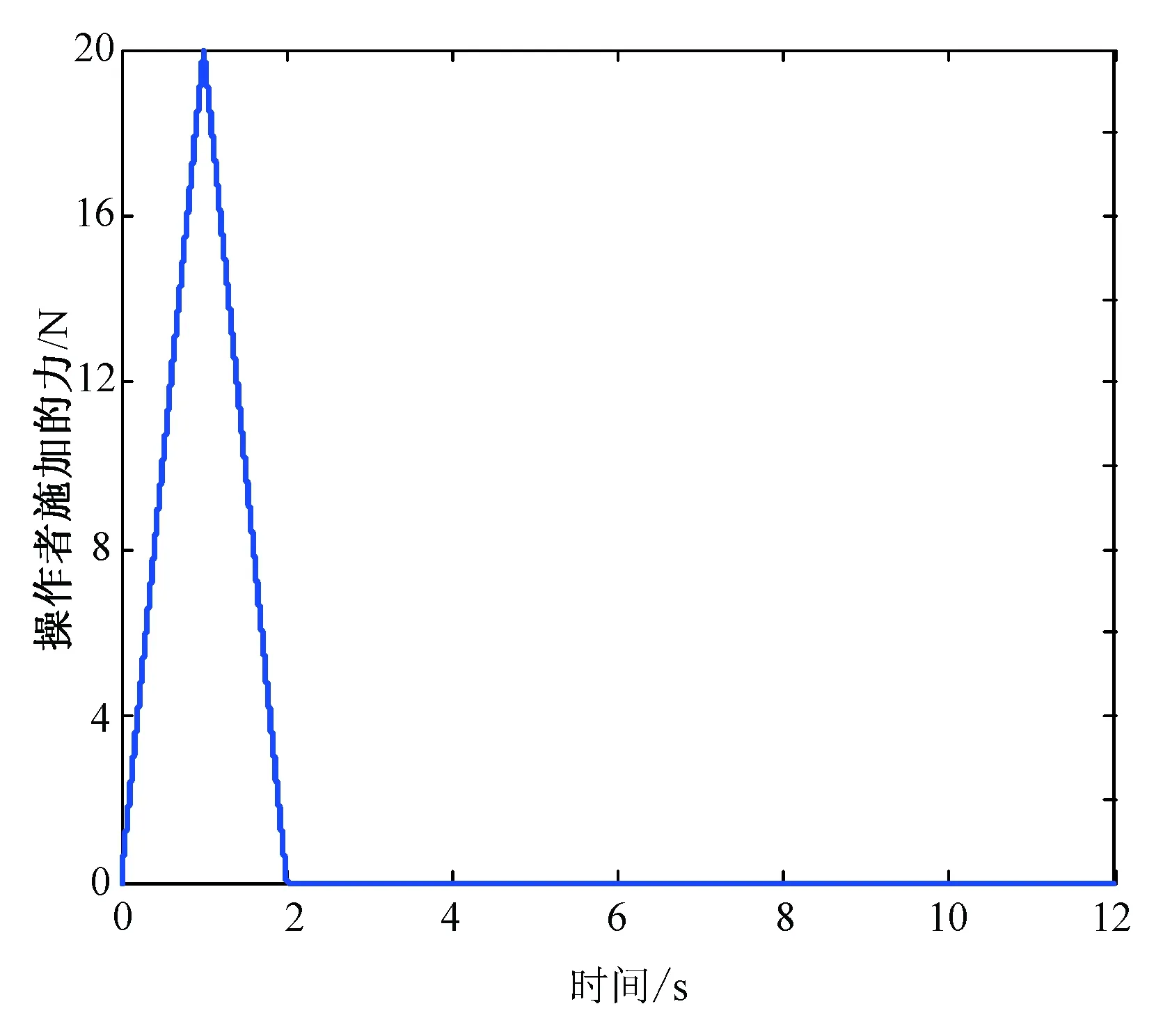
屬性1[1]:Mi(qi)為對稱正定慣性矩陣,存在正常數mi1和mi2使不等式mi1I (2) (3) 首先,考慮當系統狀態滿足|x| (4) 引理1[9]:對于任意正常數Nb以及向量?x∈Rm,在區間‖x‖ (5) 定義2[20]:定義任意連續函數N(ζ):R→R當其滿足 (6) 時,則稱其為Nussbaum類型函數。 引理2[21]:V(·)和ζ(·)為定義在[0,tf)上的光滑函數,?t∈[0,tf)使得V(·)≥0。N(ζ)為光滑的Nussbaum類型函數,且為偶函數,若對任意的t∈[0,tf),可使如下不等式成立: (7) 其中,c0>0,c1>0為常數,η為時變參數。 引理3[22]:Γ為m×m的對稱矩陣且x∈Rm為非零向量,定義ρ=(xTΓx/xTx),則Γ分別在[ρ,∞)和(-∞,ρ]上至少存在一個特征值。 (8) xTRix=βi(t)xTx, (9) 為處理未知函數βi(t),本文采用了形如式(5)的Nussbaum增益函數N(ζ)=eζ2cosζ。 神經網絡因其強大的函數逼近能力,學習能力以及很好的容錯力,在非線性系統控制中得到了廣泛的應用。而徑向基神經網絡(RBFNN)因其簡單、線性化參數結構的特點得到迅速發展。一個未知非線性函數f(Z):Rl→Rm1在集合ΩZ∈Rl上可通過徑向基神經網絡在線逼近[22],可描述為 f(Z)=WTJ(Z)+δZ(Z), (10) 其中,Z∈ΩZ?Rl為神經網絡輸入,W∈Rp1×m1為徑向基神經網絡(RBFNN)的最優權重矢量,p1>1為神經元個數,δZ∈Rm1表示近似誤差,J(Z)=[φ1(Z),…,φp1(Z)]T∈Rp1為已知的光滑基函數向量,φi(Z)(i=1,2,…,p1)通常選為高斯函數: (11) 為保證非對稱時變時滯下不確定閉環遙操作系統在全狀態時變約束下的穩定運行,首先通過設計新的非線性觀測器,基于帶有時變時延的位置信息獲得相應的速度和加速度信息;其次,針對實際約束條件選取合適的BLF,并設計新的自適應神經網絡控制器;最后,通過證明所選取BLF的有界性,從而可得閉環遙操作系統穩定,且系統狀態始終處于預設的范圍以內的結論。 首先,定義主-從位置同步誤差: (12) 其中,Tm(t)表示信號由主端傳遞到從端的時間延遲,Ts(t)表示信號由遠處的從端傳遞到主端的時間延遲。進而定義 (13) 其中,αm1,αs1為虛擬控制器,虛擬控制器的設計將在后續給出。 進一步,關節速度同步誤差給出如下: (14) 顯然,Dm和Ds中含有時變時延導數信息。實際中,時延導數信息很難精確測得。針對該問題,本文設計新的非線性觀測器,在線估計Dm和Ds,并在控制器中進行補償[25]。 針對系統(13)設計如下非線性觀測器: (15) (16) 結合式(14)、(15)和(16),可得觀測器觀測誤差方程為 (17) (18) 引理4的具體證明可參考文獻[26]。 注2:本文所設計的非線性觀測器可實現對網絡傳輸時延導數所產生的不確定項進行快速、精確估計,進而可在控制器設計中進行消除。在保證時變時延下閉環遙操作系統穩定性的同時,可以提高主-從機器人之間的同步精度。 遙操作系統中,主端機器人一般由操作者操控,而從機器人通常位于遠端完成各種復雜任務,考慮到從機器人在實際應用中可能存在的環境約束,同時出于安全考慮,人為限定從機器人的工作范圍。由于從端任務的不斷改變,不對稱時變約束更加符合實際應用需求,所以本文針對從端機器人考慮了時變非對稱約束下的全狀態約束控制器設計問題。下面給出控制器的設計過程及系統穩定性的證明。 第一步:選取BLF如下: (19) 其中,zs1j表示向量zs1的第j個變量,且該定義同樣適用于其他變量,Nbb1(t),Nab1(t)為非對稱時變約束值,定義集合:Ωzs1:{zs1j|-Nab1(t)<|zs1j| 對V1求導并結合式(12)可得 (20) 虛擬控制器αm1,αs1設計如下: (21) 將式(21)代入(20)可得 第二步:選取新的BLF: (22) 其中,Nbb2(t),Nab2(t)表示時變非對稱約束,定義集合:Ωzs2:{zs2j|-Nab2(t)<|zs2j| 同樣對V2進行求導: (23) (24) 結合楊氏不等式可以得如下不等式: 由此可得 利用上述不等式對式(24)進行放縮: 根據方程(6)定義的Nussbaum增益函數,設計自適應神經控制方案如下: (25) (26) (27) 定理1考慮雙邊遙操作系統(1),采用自適應神經網絡控制器(24)以及自適應調節律(25)和(26),當初始條件滿足:zs1(0)∈Ωs1:={zs1∈Rn:Nab1<|zs1j| -Nab1<|zs1j| 證明:選取Lyapunov函數如下: (28) (29) (30) 結合引理1得如下不等式: 將上述不等式帶入式(30): (31) 其中,μ=min{2km1,2cm1,2ks1,2cs1,κm,κs}, 對式(31)兩邊進行積分: 此外,從機器人狀態一直處于約束界內,即 -Nab1<|zs1j| 證畢。 為驗證本文所提出的自適應神經網絡全狀態約束控制器的有效性,仿真中考慮了由兩個相同的2自由度機械臂組成遙操作系統,仿真中2自由度機器人系統的模型定義為 g1(q)=g(m2l2cos(q1+q2)+(m1+m2)l1cos(q1)), 操作者施加到主機器人的力如圖1所示。在操作者施加力的作用下主機器人開始移動,并將自己的位置和速度信息通過網絡傳輸通道傳輸至從機器人端。進而,從機器人在控制器作用下跟隨主機器人運動。 圖1 操作者施加到主機器人的力Fig.1 Force inserted by the operator to the master 主-從機器人之間的位置同步誤差如圖2所示。從圖2可以看出,在本文設計的自適應神經網絡全狀態約束控制器下,當操作者施加的力為零后,主、從同步誤差將在1.5 s收斂至零點。且主-從位置同步誤差始終處于被約束的時變約束范圍內。因此從圖2可以看出,操作者可以通過控制主機器人的運動使得從機器人跟隨主機器人運動而完成特定的作業。由于主機器人位置有界,且主-從機器人位置誤差有界,可得從機器人位置有界的結論,因此可知從機器人位置滿足約束條件。 圖2 從端關節同步誤差Fig.2 Synchronization errors at slave side 進而,從機器人的關節速度約束變量示意圖給出如圖3所示。從圖3可以看出,在本文設計的控制器下,當操作者施加力為零時,從機器人速度快速趨于零點,且主-從機器人速度誤差始終處于所約束的范圍內。由于主機器人在操作者的控制下速度信號始終有界,且主-從速度誤差有界,因此可得從機器人速度有界的結論。最終表明從機器人速度始終處于受限的范圍以內。 圖3 從機器人速度受限信號Fig.3 Constrained velocity signal at slave side 以上仿真結果,充分驗證了本文所設計控制器在系統存在模型和參數不確定、未知外界干擾、非對稱時變時延以及全狀態時變約束下控制的有效性。 本文針對全狀態時變約束條件下,帶有系統不確定性和非對稱時變時延的遙操作系統的同步控制問題進行了研究。創新性地將全狀態時變約束問題轉化為系統的穩定性問題,提高了主-從系統同步精度的同時,避免了因系統狀態突然增大導致的碰撞問題。通過引入新的非線性觀測器保證了閉環遙操作系統在非對稱時變時延下的穩定性。進而,引入徑向基神經網絡在線估計系統動態不確定性,并應用Nussbaum增益處理系統輸入矩陣不確定的問題。通過構造新的障礙Lyapunov函數證明了主-從系統的穩定性和同步性能。最后,仿真結果驗證了本文設計方案的有效性。
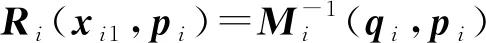
1.2 障礙Lyapunov函數
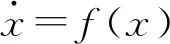
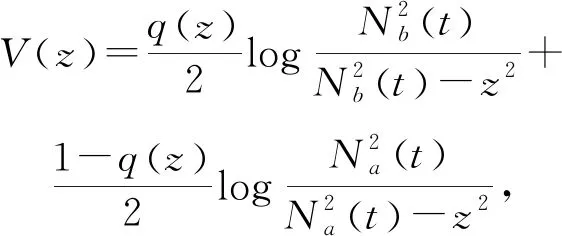
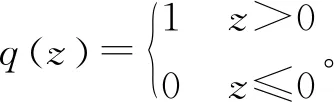

1.3 Nussbaum增益
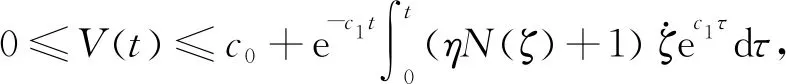
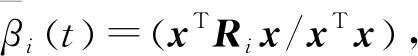
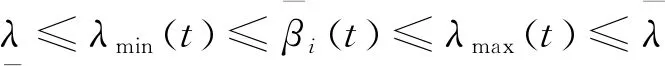
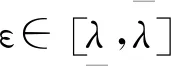

1.4 徑向基神經網絡


2 控制器設計及穩定性分析
2.1 非線性觀測器設計
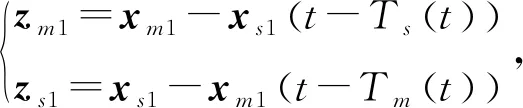
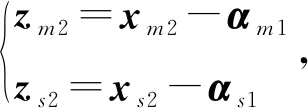

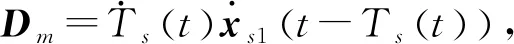
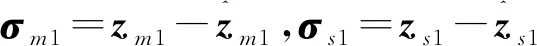

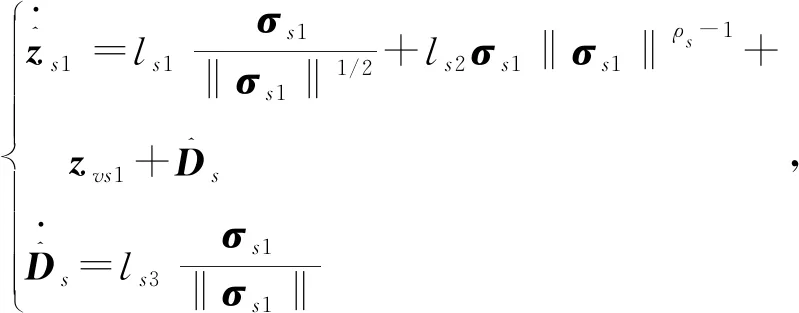
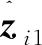
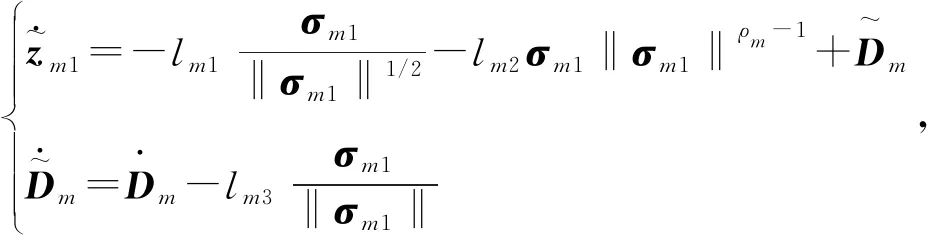
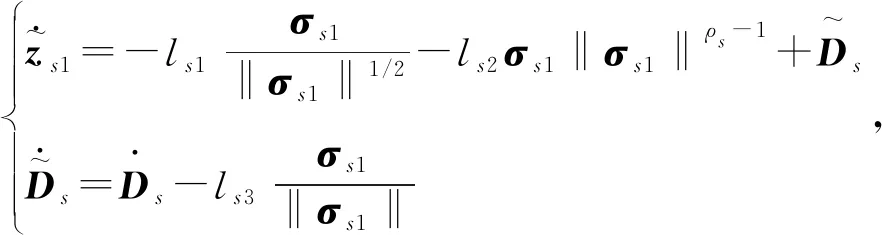

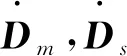
2.2 全狀態約束控制器的設計

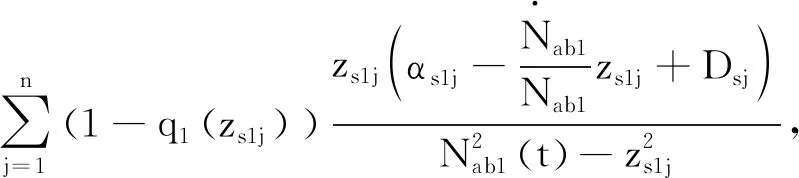
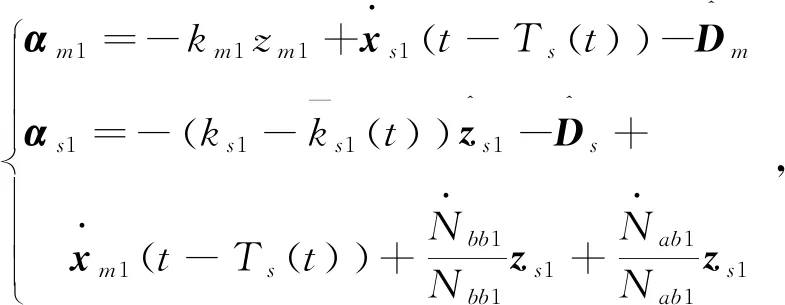

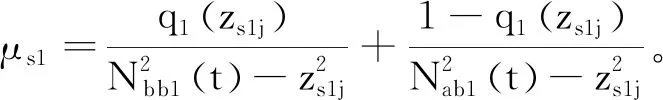
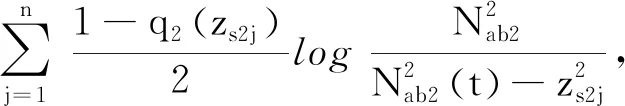
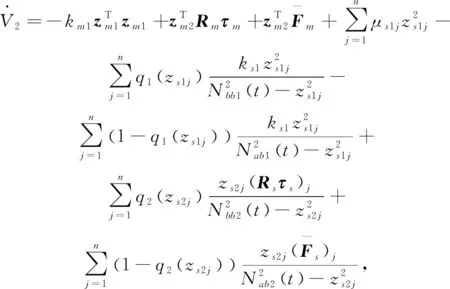
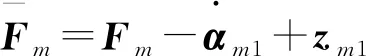
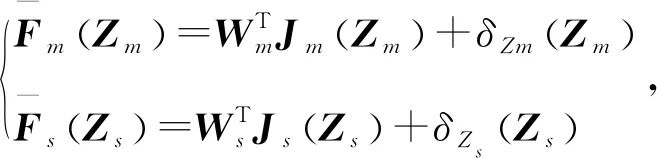
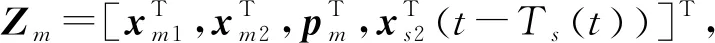
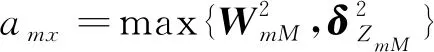
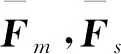

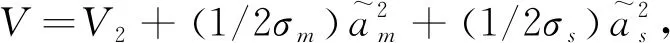
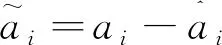
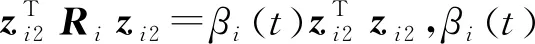


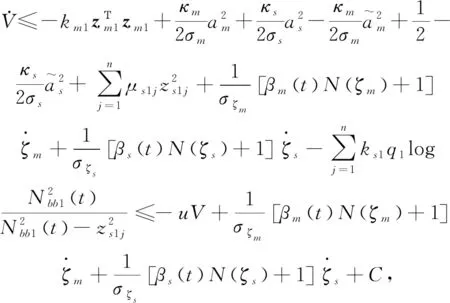

3 仿真實例
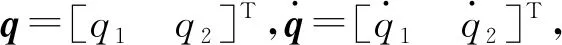

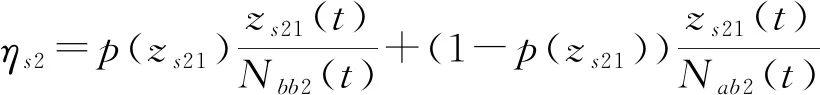


4 結論

