受端電網STATCOM布點及容量規劃的凸松弛方法

馬騫，鄧卓明，吳云亮，李鵬，姚文峰，郭知非

(1.中國南方電網電力調度控制中心，廣州510663；2. 南方電網科學研究院，廣州510663)

0 引言

受端電網的電能往往由其外部遠距離的發電廠通過高壓輸電線傳輸獲取，并且對應著密集的工商業負荷，換流站、輸電線路以及異步電動機、電弧爐、降溫壓縮電機等負荷的無功功率需求量巨大[1]。在負荷側安裝一定數量和容量的靜止同步補償器(static synchronous compensator, STATCOM)做無功補償，不僅能在電網穩定運行時維持電壓穩定、提高供電質量、降低電能損耗，同時在發生較為嚴重的短路故障時，能提供堅強的無功支撐，快速恢復電壓至安全水平，避免甩負荷。目前在經濟條件相對較好的廣東電網，已經逐漸在負荷端如東莞、水鄉配置了STATCOM[2]。STATCOM的規劃和控制也獲得了越來越多的關注。文獻[3]提出了在多直流饋入系統各母線對多回直流逆變站電壓支撐強度的指標，并用于南方電網STATCOM配置方案的研究。文獻[4]描述并復現了HVDC系統在故障恢復過程中發生“二次換相失敗”的現象，提出了根據故障的嚴重程度差異化配置STATCOM無功補償模式。STATCOM作為一種新興的電力電子無功補償裝置，盡管有著極其優秀的無功補償性能(反應時間短，補償容量靈活多變)，但是其造價仍然高昂，規劃配置STATCOM必須精打細算，避免電網投資的浪費[5]。

目前電網規劃人員對STATCOM的規劃配置大多采用枚舉試錯的方式，通過大量的仿真試驗獲得滿足安全約束的規劃方案。然而，大量的仿真試錯不僅工作量巨大、耗費大量的時間，而且獲得的規劃方案也僅僅是一個相對較好、能滿足安全約束的方案，并不是最經濟的方案。并且現代電力系統模型越來越復雜，規模也越來越大，組合爆炸的問題將導致枚舉無法進行。

因此，國內外一些文獻提出了數學化的規劃方案。在規劃STATCOM的配置時，需要考慮STATCOM的安裝地點以及安裝容量，即對應定點和定容的規劃。對此國內外已有相應的研究成果。文獻[6 - 7]采用基于動態無功—電壓靈敏度的電壓控制敏感因子和多饋入相互作用因子，計算獲得電壓控制敏感點，以便確定動態無功源的布點。在此基礎獲得候選節點后，文獻[8]進一步采用基于分解的多目標進化算法確定動態無功源的容量。文獻[9]指定動態無功—電壓靈敏度最大的節點為候選節點，然后指定STATCOM的容量為對應節點補償的上限值。文獻[10]利用軌跡靈敏度計算和奇異值分解確定動態無功源的布點，然后通過時域仿真和非線性優化之間的交替迭代獲得規劃容量。盡管上述的方法能夠獲得相對較好的、工程上能用的規劃方案，然而，因為它們把動態無功源布點及容量完全割裂開來，獲得的規劃方案只是布點和容量二層的分別最優，并不是它們整體的最優方案。

為此，本文分別采用整數變量和連續變量表征STATCOM的安裝地點和安裝容量，把整體的規劃問題解析為數學上的混合整數規劃模型，以便獲得布點和容量規劃的整體最優方案。為了提高求解效率，本文采取了凸松弛技術[11 - 13]，借助STATCOM布點的某些特征，關于整數變量整體凸化原始的混合整數規劃模型，然后對凸模型實施一種緊松弛。經算例驗算，本文的混合整數規劃模型和凸松弛技術能夠獲得STATCOM定點和容量的最優規劃方案，有效緩解電網短期電壓失穩的問題。同時，相比割裂布點和容量的傳統規劃方法，本文的方法獲得的規劃方案更優，即規劃的費用更小。本文的創新在于提出一個通用的混合整數規劃模型和凸松弛求解方案，避免大規模枚舉和試錯仿真工作，并且獲得最經濟的規劃方案。同時，得益于電網元器件的模型的通用性，本文提出的優化模型可以實施封裝，后續可以根據用戶需要對模型進行修改，從而推廣到其他的電網。該模型的通用性將可以節省大量仿真試錯的工作量和時間。

1 STATCOM規劃的混合整數規劃模型

1.1 目標函數

本文目標函數J(·)定義為STATCOM規劃方案的投資費用，包括與基建相關的固定安裝費用(例如征地補償)以及與容量相關的容量費用(例如設備購置)2個部分。STATCOM總體的規劃投資費用由固定安裝費用和容量費用疊加[14]。

J(·)=vT[c1e+c2·(QCmax-QLmax)]

(1)

式中：v為STATCOM安裝地點的二進制列向量(即所有元素皆為二進制數值)，其中第i個元素的數值為0，代表候選節點i不安裝STATCOM，無需記及固定安裝費用和容量費用，第i個元素的數值為1，代表候選節點i安裝STATCOM，需要記及固定安裝費用和容量費用；c1為固定安裝費用，萬元；c2單位容量費用，萬元/Mvar；e為單位列向量；QCmax=[qc1,qc2,qc3,…,qci]為STATCOM的容性輸出限值列向量；QLmax=[ql1,ql2,ql3, …,qli]為STATCOM的感性輸出限值列向量；其中第i個元素qci和qli分別對應候選節點i的容性容量(正值)和感性容量限值(負值)。需要注意的是，QCmax和QLmax均為可參與優化的變量，而不是固定不變的參數。

在極小化目標函數(即規劃投資費用)的過程中，各個站址STATCOM的配置容量(即QCmax-QLmax)會逐漸下降直至收斂，極小化目標函數能夠限值各個站址的配置容量。

1.2 電壓和功角安全約束

根據南方電網安全穩定導則，電壓安全約束為故障清除1 s時間內，節點電壓恢復至0.75 p.u.以上。

Vl.k(t)≥0.75,t∈[tc+Td,tf]

(2)

式中：l和k分別為節點編號和故障編號；t為仿真時刻；tc和tf分別為故障清除時刻和仿真終止時刻；Td為持續時間1 s；Vl.k(t)為節點電壓。

功角安全約束則必須保證所有發電機功角與慣量中心轉子角的功角差小于給定的數值120 °。

|δg.k(t)-δCOI.k(t)|≤δmax

(3)

式中：g為發電機編號；δg.k(t)為發電機功角；δmax為給定的閾值120 °；δCOI.k(t)為慣量中心轉子角。

(4)

式中：Mg為發電機慣量；NG為發電機數量。

此外，約束條件還應包括動態設備的微分代數方程、系統的潮流方程、變量上下限約束以及邊界約束等等。因為這些方程都比較常規且繁瑣，此處不一一列舉，具體的方程可參考文獻[9,15]。其中，發電機采用經典四階模型，勵磁系統采用經典四階模型，異步電機負荷采用經典三階模型，STATCOM采用增益-時間-常數模型。

1.3 STATCOM容量約束

在實際工程中，各個站址由于場地、檢修等限制，可能存在數值不相等的受限容量。該限制可以通過控制變量QCmax和QLmax的上下限約束(不等式約束)表達。

(5)

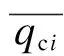
1.4 混合整數規劃模型

STATCOM規劃問題的混合整數規劃模型可采用簡約形式表示，具體如式(6a)—(6e)所示。

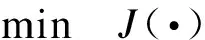
(6a)

(6b)

0=Gk(xk(t),yk(t),u,v)

(6c)

0≤Hk(xk(t),yk(t),u)

(6d)

v∈{0, 1},t∈[t0,tf]

(6e)

式中：xk(t)、yk(t)、u、v分別為狀態變量、代數變量、連續決策變量(即規劃安裝容量)以及二進制決策變量(即規劃安裝布點)的列向量；t0為仿真起始時刻；在方程方面，式(6b) 為微分方程，包含發電機及其勵磁系統、異步電機負荷以及STATCOM的動態；式(6c)為受端電網的潮流方程，其中STATCOM以注入功率的形式掛在對應節點上；式(6d)包含所有變量(狀態變量、代數變量和決策變量)的上下限約束以及1.2節提到的電壓和功角安全約束。關于式(6b)提到的設備模型和微分方程可參考文獻[9,15]。

2 混合整數規劃模型的凸松弛

凸松弛方法是一種針對和處理混合整數規劃問題的處理方案。經過凸松弛處理，混合整數規劃的求解效率可以極大提高。凸松弛包含2個步驟：凸化以及松弛。

凸化過程需要列舉二進制決策變量的所有可能組合，然后混合整數規劃模型整體關于二進制決策變量做線性疊加。

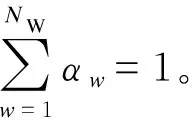
線性疊加可以使得規劃模型關于二進制變量整體凸化。因為STATCOM以注入功率掛在潮流方程對應節點，該功率存在與否是由決策變量v決定的。因此潮流方程(6c)是直接與v相關的。此外，在1.1節介紹過目標函數也是與v直接相關的。除此以外，微分方程、上下限約束和安全約束都沒有與v直接相關。因此只需對式(6a)和(6c)做關于二進制變量的線性疊加即可。

本文借用一個虛擬4節點網絡為例子詳細介紹凸化。假定在該虛擬的4節點網絡中，節點1—3為負荷節點，并被選為STATCOM的候選節點，節點4是平衡節點。因為在此案例共3個候選節點，每個節點安裝或不安裝(1/0)共2種情況，共有8種布點方案，具體如表1所示。

表1 虛擬案例的8種布點方案Tab.1 Eight plans of locations in the virtual case

為表1中每種組合引入替代變量αw。 依據線性疊加的計算，節點1—3的潮流方程可分別凸化為：

(7a)

(7b)

(7c)

式中Gl.k(xl.k,yl.k,ul,vl.w)和vl.w分別為節點l的潮流方程函數以及vw的具體值。

由表1和式(7a)—(7c)可知，因為整數決策變量共8種組合，凸化需要枚舉8次，引入8個替代變量，才能完成線性疊加。然而，α1-α8實際并非獨立變量，可以做一定的簡化。在對應的潮流方程上分別引入變量θ1.1=α1+α2+α3+α5，θ1.2=α4+α6+α7+α8，θ2.1=α1+α2+α4+α6，θ2.2=α3+α5+α7+α8，θ3.1=α1+α3+α4+α7， 以及θ3.2=α2+α5+α6+α8， 其中θl.i代表節點l的第i個θ變量。式(7a)—(7c)可簡化為：

0=G1.k(x1.k,y1.k,u1, 0)θ1.1+G1.k(x1.k,y1.k,u1, 1)θ1.2

(8a)

0=G2.k(x2.k,y2.k,u2, 0)θ2.1+G2.k(x2.k,y2.k,u2, 1)θ2.2

(8b)

0=G3.k(x3.k,y3.k,u3, 0)θ3.1+G3.k(x3.k,y3.k,u3, 1)θ3.2

(8c)

并且同樣滿足θ1.1+θ1.2=1，θ2.1+θ2.2=1以及θ3.1+θ3.2=1的約束條件，且θl.i為二進制變量。這是因為STATCOM以注入功率掛在負荷節點上，節點l安裝STATCOM與否只影響節點l列寫潮流方程，并不影響其他節點列寫相應的潮流方程，因此節點間列寫潮流方程是相互獨立的。

同理，對于目標函數J(·)， 假定Jl(ul,vl.w)是節點l規劃安裝STATCOM的費用，則目標函數可凸化如式(9)所示。

(9)

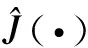
松弛過程則把上述的替代變量θl.i從二進制的取值范圍松弛至連續區間[0,1]，混合整數規劃模型整體轉換為連續規劃問題，從而避免了直接求解混合整數規劃問題。在優化領域，基于梯度的算法或求解器都能比較高效地求解連續規劃問題，因此提高了STATCOM規劃的效率。同時，經文獻[11 - 13]的驗證，上述關于整數變量的凸化及松弛是一個緊松弛過程，可以獲得滿足邊界條件約束的規劃方案。

3 整體規劃流程

依據上述的混合整數規劃模型以及凸松弛方法，本文歸納了STATCOM的整體規劃流程如下。

1)采用三相接地短路故障N-2掃描受端電網薄弱區域，獲得電網在規劃STATCOM前的短期電壓失穩的故障集；

2)以安裝費用最小為目標函數，建立全網電壓安全約束的STATCOM布點及容量規劃的規劃模型式(6a)—(6e)；

3)枚舉二進制布點變量v的所有組合，采用固定的列向量vw(w= 1, 2,…,NW)代表對應的每1種規劃方案；

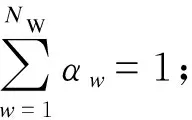
5)關于二進制變量，整體做線性疊加以凸化混合整數規劃模型；

6)松弛替代變量θl.i至連續區間[0,1]；

7)在通用代數建模系統(general algebraic modeling system，GAMS)上調用CONOPT求解器[16]求解經過凸松弛處理后的連續優化模型，獲得STATCOM布點及容量規劃方案；

8)采用PSD-BPA軟件仿真校驗規劃方案是否滿足暫態電壓、功角穩定約束。

4 算例分析

本文在2個系統上實施了上述的規劃方法。系統A是IEEE標準39節點測試網絡，包含有10發電機、39節點以及17異步電機。系統B是廣東省級電網，包含有181發電機、1 009節點以及361異步電機。本章的算例計算是在一臺高性能服務器上完成的，它具有16組Dell M620刀片機，每個刀片又配有2個Xeon E5- 2650處理器(其中每個處理器都是8核8線程)和128 GB的運行內存。計算平臺分別采用GAMS 24.4.6做優化計算[16]，MATLAB 2015a 做編程，以及PSD-BPA做時域仿真[17]。在上述2個測試系統上進行N-2掃描，分別獲得6個短期電壓失穩的故障組成故障集。以下STATCOM的布點和容量規劃將解決故障集導致的短期電壓失穩問題。

首先以系統A為例子，把本文的規劃方法對比傳統的布點及容量完全割裂的規劃方法，即先通過靈敏度計算確定安裝地點再確定安裝容量。經過計算，表2列舉了本文的布點和容量統一規劃方案，共需6臺STATCOM，配置總容量為286.52 Mvar。表3列舉了傳統的布點及容量完全割裂的規劃方案，同樣需要6臺STATCOM共338.68 Mvar。由2個表格可看出，雖然兩個方案需要的STATCOM數量即布點數相同，但本文的布點和容量統一規劃方案需要的容量和費用遠小于傳統的規劃方法，因此更加經濟，是安裝地點和安裝容量整體的最優結果；而傳統的做法僅僅只是安裝地點和安裝容量的分別最優。

表2 本文的布點和容量統一規劃方案Tab.2 Unified plan of location and capacity in this paper Mvar

STATCOM的規劃難點在于混合整數規劃。有學者指出，如果全體負荷母線均為STATCOM備選安裝點，只規劃STATCOM容量，即可避免混合整數規劃問題。然而，該方法只能最小化容量的規劃，卻無法記及STATCOM的固定安裝費用c1。STATCOM總體投資費用變得很大，因為幾乎所有母線都規劃安裝STATCOM。

同樣以系統A為例，如果所有負荷點均為STATCOM的規劃節點，以此極小化STATCOM的規劃容量。該規劃方案列舉在圖1中，在17個負荷

表3 傳統的布點及容量完全割裂的規劃方案Tab.3 Conventional separated plan of location and capacity Mvar

節點的規劃容量共219.28 Mvar，略小于表2即本文方案的286.52 Mvar。但是，圖1的規劃方案中，規劃容量被分散到17臺STATCOM，數量較大，因此基建費用較高。對應的STATCOM規劃費用是32 716.52 萬元，遠高于表2的方案20 691.087 萬元。因此在實際運行中，南方電網較多情況是集中安裝少量的大容量STATCOM以減少基建費用，提高投資的效率。

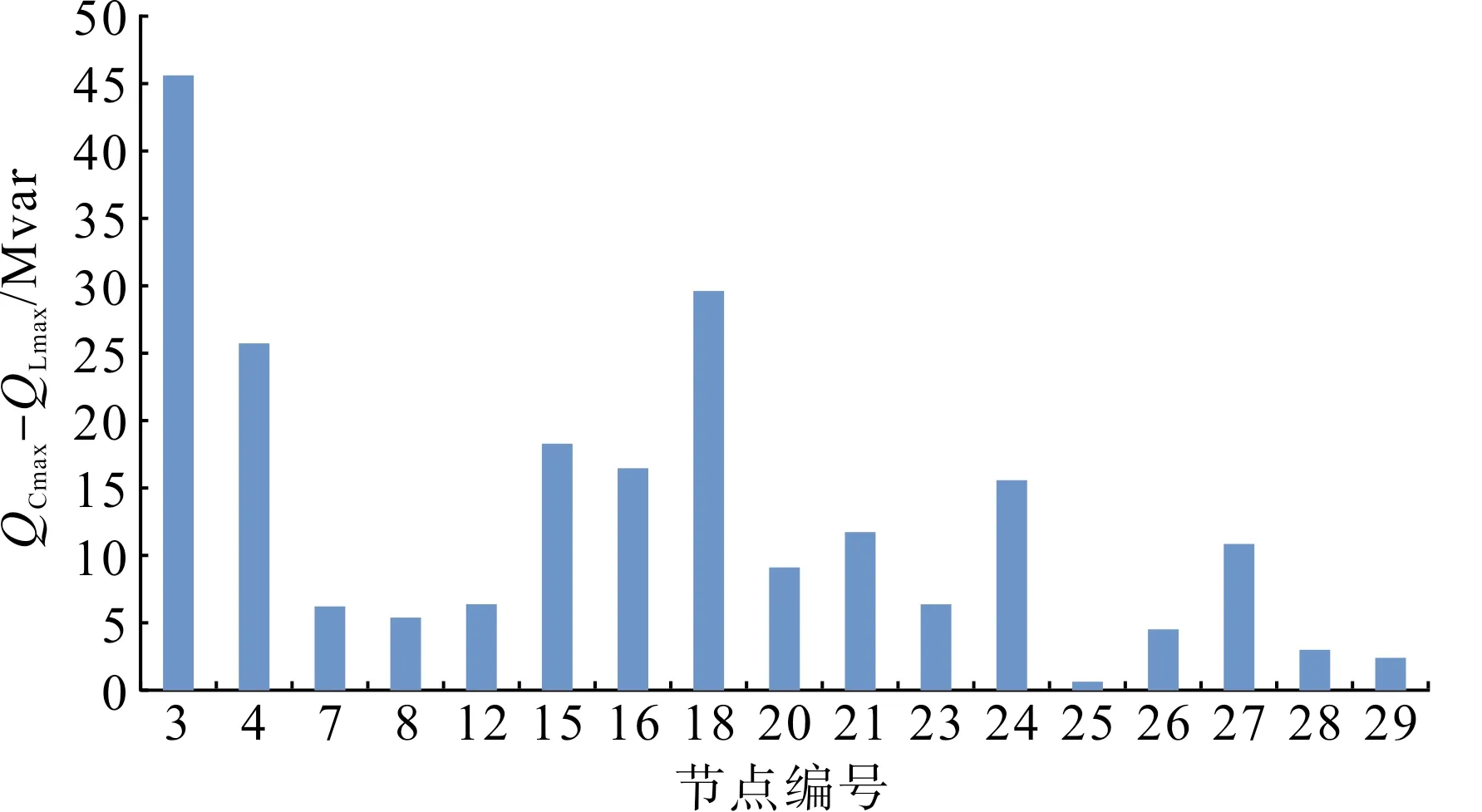
圖1 STATCOM在所有負荷節點的規劃容量Fig.1 Capacities of STATCOM at all of the loads

為了驗證本文凸松弛方法的正確性，系統A作為公共可用的IEEE測試系統，其算例用于案例的比較和復現。傳統的布點及容量完全割裂的規劃方法或者標準求解器，在涉及大型實際電網案例時會面臨巨大的求解壓力；相反，它們可以快捷地求解系統A類的測試系統，并提供相應的計算結果，作為凸松弛方法的對比。在另一方面，系統B作為一個實際省級電網，其算例可驗證凸松弛方法求解STATCOM布點及容量規劃問題的高效性。在此算例上，凸松弛方法在可接受的時間框架內可獲取STATCOM規劃問題的方案，然而像SBB這種求解器卻不能完成，足以驗證凸松弛方法的高效性。

如圖2所示，系統B在故障集下節點電壓恢復緩慢，大量節點在故障清除1 s后仍然不能恢復0.75 p.u.以上，短期電壓失穩。采用本文凸松弛算法計算獲得的STATCOM規劃方案如表4所示。在該規劃方案下，如圖3所示，系統B能夠恢復短期電壓安全。

圖2 系統B在故障集下的電壓軌跡Fig.2 Voltages of system B under contingency set

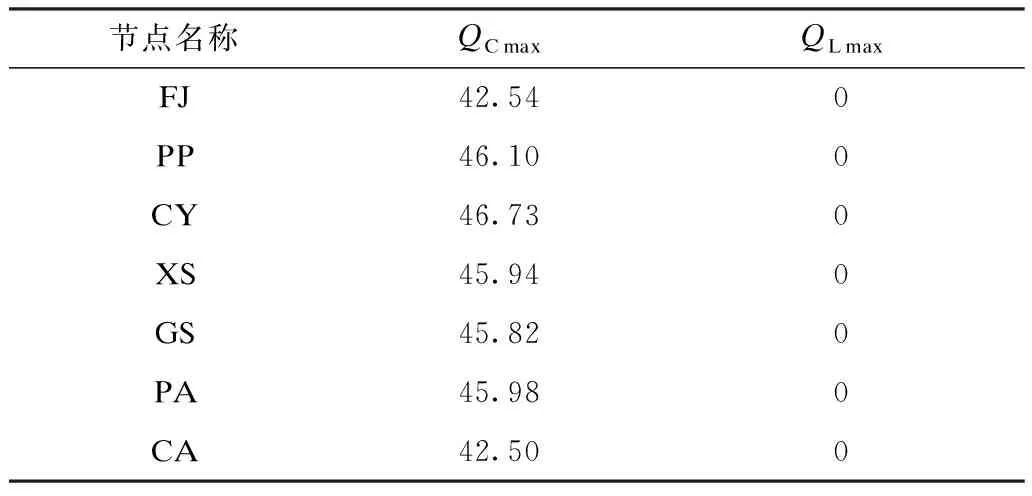
表4 系統B的STATCOM規劃方案Tab.4 Planning of STATCOM for system B

圖3 含STATCOM規劃的系統B在故障集下的電壓Fig.3 Voltages of system B under contingency set with planning of STATCOM

針對混合整數規劃，目前存在成熟的商業求解器SBB。SBB求解器是GAMS平臺上其中一種較為流行和通用的混合整數非線性規劃求解器。SBB結合了求解混合整數線性規劃的分支定界(branch and bound，B&B)方法以及某些標準的非線性規劃求解器(可供用戶選擇)如MINOS、SNOPT。在求解混合整數非線性規劃問題時，SBB先對整數規劃部分實施分支定界，求取一個相對較好的整數規劃結果，然后再基于用戶選擇的非線性規劃求解器對非線性規劃部分實施求解，從而獲得混合整數非線性規劃的結果。筆者在從事混合整數非線性規劃問題研究的時候，先后比較過BARON、DICOPT、SBB等混合整數非線性規劃求解器，最后發現SBB求解器對于本文的STATCOM布點及容量規劃問題具有較好的求解效果。因此，文章最后將本文的凸松弛方法和SBB求解器的結果進行對比，以便驗證本文方法的有效性和高效性。如表5展示了本文規劃方法與SBB求解器的結果對比。

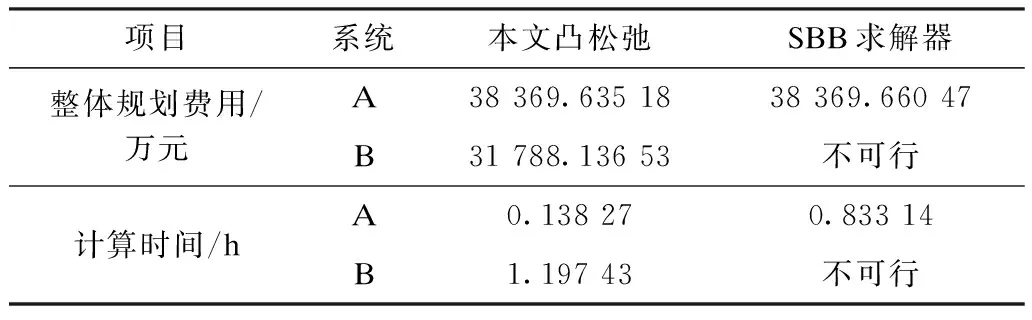
表5 本文方法和SBB求解器計算結果的比較Tab.5 Comparison of the results between the method in this paper and the SBB solver

在規模比較小的系統A中，凸松弛方法與SBB求解器的STATCOM整體規劃費用基本一致，相差無幾，因此本文的規劃方案是可靠的。并且，本文凸松弛方法的計算時間遠短于SBB求解器，說明凸松弛方法的求解效率更高。面對大規模系統B的STATCOM規劃，SBB求解器需要求解大型混合整數規劃問題，在花費較長時間后仍然不能獲得STATCOM的規劃方案。整數規劃問題可以理解為組合優化問題，而組合優化問題的規模隨著控制變量數量的增加呈現指數增長，極其容易引發數學上的指數爆炸問題。對于實際1 009節點系統B的規劃問題，由于節點數量龐大，其控制變量(包括STATCOM的規劃容量和安裝地點)的數量也相應非常大。一般而言，當控制變量的數量大于20，組合的數量已經超過百萬。如此龐大的組合數量，在上述分支定界的過程要存儲很多分支和葉子節點，花費很多內存空間。分支定界法的求解效率基本上由值界方法決定，若界估計不好，在極端情況下將與窮舉搜索沒多大區別，在有限的時間內不能計算所有的組合。因此，面對1 009節點系統B，SBB求解器不能獲得最優解，其本質原因是變量的數量太大，同時組合數量指數式增長，出現了整數規劃的指數爆炸問題。但凸松弛方法不需要直接求解混合整數優化，只需要求解連續的優化問題。許多經典的基于梯度的優化方法，如內點法，可以輕松獲得最優解，因此凸松弛方法在系統B仍然得到了最優的規劃方案。因此，本文的規劃方法更適用于南方電網的STATCOM規劃。

5 結語

本文針對受端電網STATCOM的布點和容量規劃問題，采用了布點和容量統一規劃的混合整數規劃模型，并提出了一種針對混合整數規劃的凸松弛方法。該方法首先關于整數變量整體凸化混合整數規劃模型，然后對凸模型實施一種緊松弛，避免直接求解混合整數規劃。

在IEEE標準39節點以及廣東電網的算例計算表明，該方法比傳統的割裂布點和容量的規劃方法的STATCOM投資費用更小。布點和容量同時規劃的必要性得到了驗證。相比商業化的求解器SBB，本文凸松弛方法更適用于在大型受端電網如廣東電網的STATCOM規劃問題，因求解效率更高，計算時間更短，容易獲得大規模規劃問題的最優解。