窮舉-混沌蟻群算法環形穿梭車模型研究

劉緒川，王 龍，梅英杰，張孟建

（1.中科芯集成電路有限公司，無錫214072；2 哈爾濱工業大學 儀器科學與工程學院，哈爾濱150001；3.貴州大學 電氣工程學院，貴陽550025）

近年來，自動化物流系統[1-2]日益廣泛地應用于煙草、機電、醫藥、食品、軍隊等領域，相關物流裝備趨于多元化，其水平和技術性能不斷提高。自動化倉庫作為物流系統中一個重要的組成部分，其不僅具有傳統倉庫的存儲功能，還具有揀選、盤點、理貨等功能，而且其設備自身及物料存取操作都能自動進行，這大大提高了倉儲效率，同時節省勞動力，受到了廣泛的關注。立體倉庫系統在食品、醫藥、煙草、玻纖、家具等行業應用日漸廣泛，以立體倉庫系統為核心的相關物流設備愈加多元化，技術水平和性能也得到不斷提高。

穿梭車又稱為軌道式自動導引車RGV[4-6]，是集多種高新技術于一體的自動搬運設備，因行駛和輸送速度快、靈活性好、自動化程度高而被廣泛應用。經過長期的發展，環形RGV 系統代替了多臺直行RGV 系統或者大量的普通輸送設備，實現物料運送目的地的自由變動，提高了輸送的效率和靈活性。環形RGV 系統其最主要的應用是作為連接立體倉庫入庫作業區站臺、出庫作業區站臺和立體倉庫站臺的紐帶，起搬運物料的作用，是立體倉庫系統主要且重要的子系統。由于環形RGV 系統采用封閉的環形軌道，RGV 單向環軌繞圈行駛，相鄰兩車之間存在防止碰撞的安全距離，針對不同項目系統的軌道數據 （直道長度、彎道長度和轉彎半徑等）、RGV 運行參數（直道行駛速度、彎道行駛速度和加速度等）、裝卸載站臺數量及位置分布、物流的需求量等參數的不同，RGV 的數量有著很大的差異[3，7-8]。

穿梭車在整個工作系統中，其效率受到出進貨口停留時間、車身長度、穿梭車數、運行速度等影響。若穿梭車過多，會造成擁堵，甚至會系統癱瘓，大大降低了工作運行效率。若穿梭車較少，雖然不會造成系統擁堵，但是會使得貨物運輸時間較長，貨物運輸的效率降低。因此合理的穿梭車調度，在合適的運行速度下，減少擁堵時間，會使得整個工作系統效率提高。

1 模型假設

假設1：為方便貨物的搬運，假設每側的進、出貨口均勻分布在軌道的直線上。

假設2：假設每輛穿梭車每次只能運送1 件貨物。

假設3：假設穿梭車裝、卸貨物的時間相同，分別為tL、tU，一個周期為T s。

假設4：假設穿梭車的貨運軌道為單軌道設計，穿梭車不能超車，只能進行停車和前進。

假設5：假設穿梭車在環形軌道上逆時針勻速運行，其速度為v。

假設6：假設每側的進、出貨口均勻地分布在軌道的起點中線兩側，其間隔為3 m。

A 側進貨口待進的貨物量為200 件，B 側總的待進貨數量為322 件。從B 側進貨、A 側出貨時，所對應的進貨口和出貨口之間的距離，其值如表1所示。

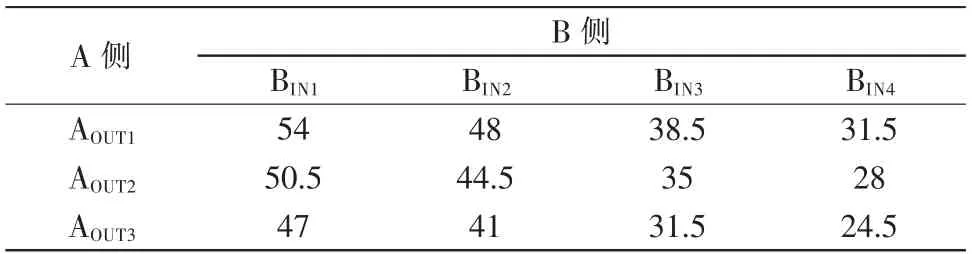
表1 B 側進貨A 側出貨對應的進貨口距離（考慮車長，m）Tab.1 Distance of the receiving port corresponding to the B-side purchasing and A-side shipping（considering the vehicle length，m）

表2 所示為一些主要符號含義。

表2 符號說明Tab.2 Symbol description

2 模型建立

考慮系統的運行效率，使得穿梭車運送貨物能夠得到高效運行，在穿梭車數量合適情況下，盡可能保證不擁堵，提高系統效率。

2.1 模型1

基于以上對問題的分析和理解，建立單個穿梭車的裝、卸貨物和運行的耗時模型，其公式如下：

式中：T1為小車在環形軌道上運行的時間；T2為小車裝、卸貨物所需的時間；T3為運行過程中等待的時間。

式中：S 為小車完成1 次裝、卸貨物在環形軌道上所通過的路程；v 為小車的行駛速度。

此外，小車裝、卸貨物所需的時間為

式中：tL為小車裝貨所需要的時間；tU為小車卸貨所需要的時間；n 為裝卸貨物的次數。

2.2 模型2

本文為了清楚地描述穿梭車的數量變化對系統的擁堵次數、完成工作量所需要的時間之間的關系。采用最小二乘多項式擬合，建立n 次多項式模型：

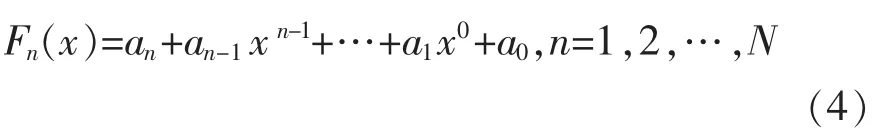
2.3 起點中線規則

為了方便后續算法分析，穿梭車軌道L=100 m，穿梭車運行速度v=1.5 m/s，裝卸貨一個周期T=10 s，軌道上出貨口7 個，進貨口6 個，考慮實際穿梭車車長約1.3 m，進出貨口寬度1 m。設計環形軌道如圖1 所示。

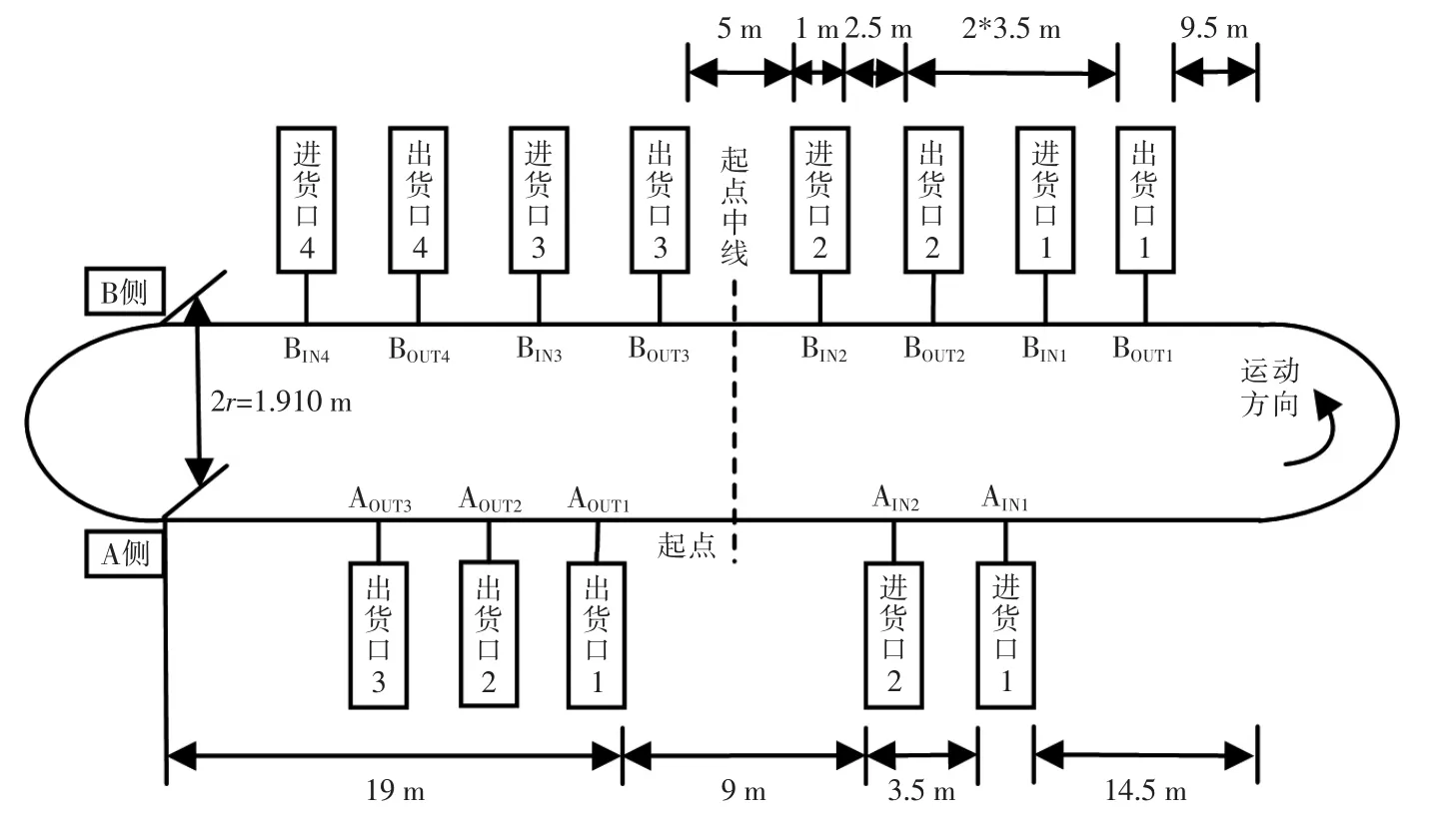
圖1 考慮車長的環形軌道示意圖Fig.1 Schematic diagram of circular track considering vehicle length

3 模型設計分析

3.1 窮舉式算法

窮舉式算法在小車數量少的情況下，可以比較精確地得到最優調度，所占用的資源也不多，其在本文的流程是：在滿足約束的情況下，保證排隊最少的情況下，小車行駛的最短距離即可當做目標最短時間。當A、B 側均有貨物時，小車優先載運B 側的貨物，并從最遠的進貨口進行裝貨，到達A 側卸貨時，以最遠的出貨口為優先出貨口；當B 側的有貨進貨口數目少于小車數量時，小車開始對A 側的進貨口進行載運，由于A 側的貨物有固定的出貨口，本文選擇dA1k和dA2k（dAjk表示A 側進貨口j 中的第k 個貨物在B 側的目標出貨口）中貨號口更大的進行載運。假設系統中N 量穿梭車Ci（i 表示從0～N），每輛車到進貨口的距離為dQjCi，則組成的矩陣為

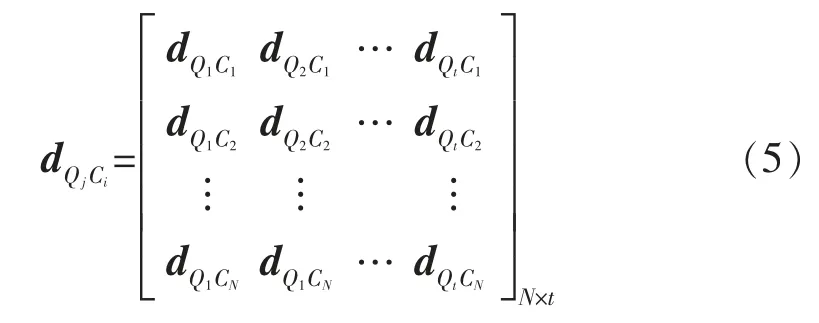
當有t 個任務時，每一輛穿梭車到對應的進貨口都有對應的距離，通過這些值可以窮舉出穿梭車的行徑組合有種；對于這些組合可以選取矩陣中不同列和不同行對應的距離之和最短的數值，因為小車排隊最少，所以該值即可當做最優解。

3.2 基于混沌蟻群算法的穿梭車處理貨物的調度規劃

由于蟻群算法[9-10]在進行穿梭車調度時存在操作時間長、收斂效率低、易陷入局部最優等缺陷。而混沌理論利用混沌運動特有的內在遍歷性、規律性和隨機性可以在一定范圍內不重復地遍尋所有狀態，跳出局部最優解，具有良好的計算精度和全局尋優能力。因此將混沌理論加入到基本蟻群算法中可有效改善基本蟻群算法的弊端，得到較優的算法，從而規劃出全局最優。因此我們建立了混沌蟻群算法模型。

混沌蟻群算法的穿梭車規劃算法流程如圖2所示。

3.3 基于蒙特卡洛的出貨口選擇算法

根據問題背景可以得到，此環形穿梭車系統共有兩側，分別為A、B 側，兩側均有進貨口，亦有出貨口。B 側的進、出口數量相等，均為4 個，將進貨口的編號 設為I，其中I＝1，2，3，4； 出貨口設 為J，J＝1，2，3，4。

而對應的A 側出貨只有3 個，因此，針對B側作為進貨口時，其出貨口位于A 側，但是出貨口的選擇是隨機的，基于這一特點，本文設計了基于蒙特卡洛的出貨口選擇算法，該算法的核心為代碼如下：

3.4 算法分析

步驟1使用蒙特卡洛的出貨口選擇算法計算出B 側作為進貨口的情況下，單輛穿梭車完成對應進貨口的工作任務所需要的時間；B 側4 個進貨口分別完成工作量所需時間。

步驟2由于A 側的進貨口有待貨出口時，每個進貨口均指定了B 對應的出貨口。因此，在計算完成貨物量所需要的時間前，應根據起點中線規則（考慮車長）計算出進貨口和出貨口之間的距離，如圖3 所示。

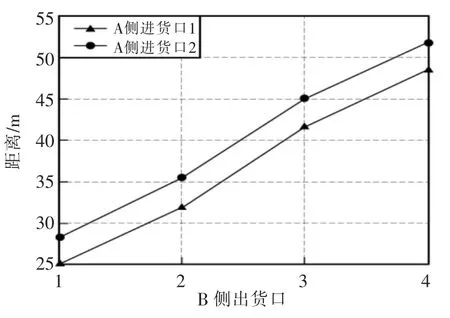
圖3 A 側進貨口與B 側各出貨口之間的距離Fig.3 Distance between A-side inlet and B-side outlet

步驟3根據穿梭車運動規則和各進、出貨口之間距離關系，使用蒙特卡洛方法進行模擬，分別取N＝1，3，6，7，9 進行計算，模擬了4 組結果，所得結果如圖4 所示。

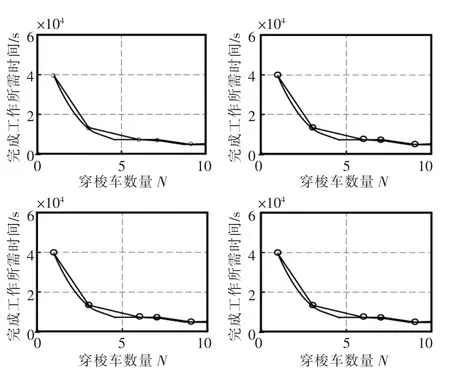
圖4 穿梭車數量與完成工作的耗時關系圖Fig.4 Relationship between the number of shuttle cars and the time taken to complete the work

從圖4 中可以明顯地看出，完成一定數量的工作量的情況下，即系統能夠接受的范圍內，完工的時間與穿梭車的數量成反比。

步驟4對環形穿梭車系統效率，我們考慮穿梭車的擁堵時間以及在單位時間內系統最大貨物吞吐量來評價系統效率。在N≤5 時，用窮舉式算法求取穿梭車擁堵時間、貨物處理總耗時以及單位時間內系統最大貨物吞吐量。在N＞5 時，用混沌蟻群算法找到最優穿梭車擁堵時間、貨物處理總耗時以及單位時間內系統最大貨物吞吐量。其擬合結果如圖5 所示。

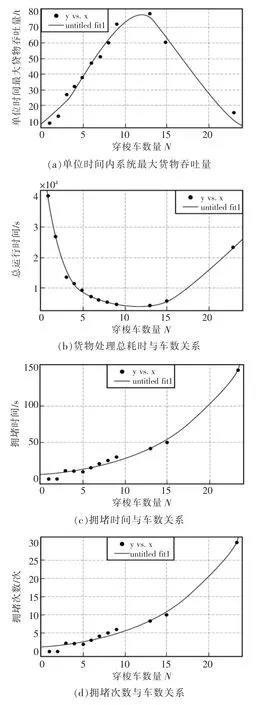
圖5 擬合結果Fig.5 Fitting results

結果表明系統的擁堵次數和擁堵時間會隨小車數目增加而明顯增加；系統的總完工時間在與穿梭車數目之間是一個先減少后增加的關系，系統在單位時間內的最大貨物吞吐量與穿梭車之間是一個先增加后減少的關系，可以得知穿梭車后期的擁堵會造成系統運行效率的降低。故為保證穿梭車系統的效率，需要選擇合適的小車數目。

4 結語

根據本文建立的模型和使用的算法，不同數量的穿梭車情況下，對單位時間貨物吞吐量、處理貨物的耗時情況、擁堵時間以及擁堵次數進行分析，找到最合適的小車數，保證系統的效率。本模型可用于工廠環形穿梭車系統的構建，實際運用中對參數的優化存在一定的實際價值，對自動化物流系統有重要意義。