基于自適應無跡卡爾曼濾波的汽車狀態參數估計
石志偉, 任師通, 魏民祥, 查曰珩
(1.山東理工大學 計算中心, 山東 淄博 255012;2.南京航空航天大學 能源與動力學院, 江蘇 南京 210016;3.江蘇省文化館, 江蘇 南京 210016)
對汽車主動安全性進行分析時,獲取汽車行駛過程中的狀態參數尤為重要。用于汽車關鍵狀態參數估計的算法主要有卡爾曼濾波算法、粒子濾波算法、滑模觀測器算法、魯棒觀測器算法和龍貝格觀測器算法等。其中粒子濾波算法易出現因密度函數建立不準確而導致粒子退化的現象;滑模觀測器算法依賴傳感器的精度和性能,否則易產生抖振現象;魯棒觀測器算法在有些情況下易產生低估估計偏差,從而引起算法發散;龍貝格觀測器算法的計算過程較復雜,不易滿足車輛估計算法的實時性要求;卡爾曼濾波算法(KF)計算簡單、收斂快速,在汽車狀態參數估計中得到廣泛應用。
汽車是一個強非線性系統,而卡爾曼濾波僅能對線性系統進行處理,在標準卡爾曼濾波算法的基礎上開發出擴展卡爾曼濾波算法(EKF)和無跡卡爾曼濾波算法(UKF)來處理非線性系統。擴展卡爾曼濾波算法通過將非線性系統的數學模型在最佳點進行泰勒展開,對非線性函數求解雅可比矩陣,從而將非線性系統線性化。采用該算法進行非線性系統線性化時,只保留一階系統,對于二階或更高階的分量采用舍棄的方法,因而存在一定估計偏差,同時當估計的目標系統非線性較強時,其計算量過大,雅可比矩陣求解復雜,易產生發散現象。而無跡卡爾曼濾波算法摒棄了求解非線性函數的雅可比矩陣,采用構造樣本點的方法將整個非線性系統線性化,進而得到一些sigma點,減少了算法的計算量。對于得到的各個sigma點,保證其均值和方差與原始采集數據相同,并將其帶入非線性系統中進行無跡變換,通過樣本加權求和使其接近高斯分布。基于高斯分布的特點,該算法可精確到三階均值和協方差,且運算簡單,得到的系統穩定。
當前的研究中,大多把觀測噪聲的協方差矩陣設定為固定值,然而車輛實際行駛過程中,過程噪聲和觀測噪聲是隨機產生的,并非固定不變,為更好地對行駛中車輛狀態參數進行實時估計,該文將不同時間段的過程噪聲和觀測噪聲設定為不同值,提出自適應無跡卡爾曼濾波(AUKF)算法。
1 三自由度車輛模型
為更好地表達車輛的真實狀態,建立具有橫向、縱向、橫擺3個自由度的車輛動力學模型(見圖1)。
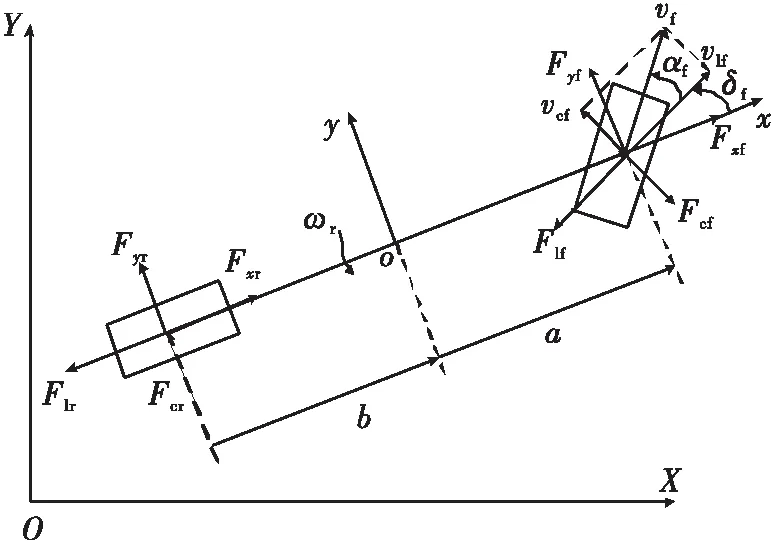
Fxf、Fyf分別為前輪在x、y軸方向受到的力;δf為前輪轉角;Fcf、Flf分別為前輪受到的縱向力和側向力;ω為橫擺角速度;Fxr、Fyr分別為后輪在x、y軸方向受到的力;Fcr、Flr分別為后輪受到的縱向力和側向力;a、b分別為質心至前軸和后軸的距離
在x軸方向,車輛的動力學方程為:
(1)
在y軸方向,車輛的動力學方程為:
(2)
在繞z軸的橫擺方向,車輛的動力學方程為:
(3)
式中:m表示汽車總質量;Iz表示車輛繞z軸的轉動慣量。
2 基于AUKF算法的汽車狀態參數估計
2.1 無跡卡爾曼原理
2.1.1 建立汽車狀態空間方程和量測方程
非線性汽車系統的狀態量為:
x=(ω,β,vx)T
(4)
式中:β為質心側偏角;vx為車輛的縱向速度。
系統控制輸入量為:
u=(δf,ax)
(5)
系統觀測量為:
y=(ay)
(6)
根據建立的三自由度汽車模型,得汽車狀態空間方程如下:
(7)
量測方程為:
(8)
將過程噪聲和測量噪聲代入汽車狀態空間和量測方程,得:
xk+1=f(xk,uk)+Q
(9)
zk+1=h(xk+1,uk)+R
(10)
式中:xk+1為k+1時刻的狀態向量;f為前一時刻狀態量與后一時刻狀態量之間的映射關系;uk為系統的控制輸入量;Q為預測過程中的噪聲;zk+1為k+1時刻的觀測向量;h為狀態向量與觀測向量之間的映射關系;R為測量過程中的噪聲。
以上2種噪聲需滿足以下關系,否則易產生協方差矩陣的非正定現象:
E[Q]=0
(11)
E[R]=0
(12)
Cov[R,Q]=0
(13)
式中:E[*]表示*的均值;Cov[*]表示*的方差。
2.1.2 無跡變換
(1) 初始均值和方差的確定:
(14)
(15)
(2) 采集點與各權值計算。1) 采集點。構造2n+1個樣本點[見式(16)]。2) 采樣點權值計算。由于存在采樣的非局部效應,需對各采樣點的權值進行一定比例修正,計算得到均值的權值見式(17),方差的權值見式(18)。
(16)

(17)
(18)
式中:λ為調節參數。
2.1.3 Sigma點的獲取
根據式(16)和式(17),可獲取一組Sigma點集,點集中包括2n+1個點,可由向量ζ表示:
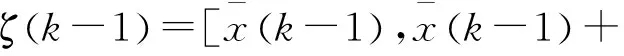
(19)
式中:i=0,1,2,…,n。
2.1.4 預測更新過程
當k大于1時,通過加權得到狀態的預測值:
(20)
預測更新后得到的均值為:
(21)
式中:q為過程噪聲的平均值。
預測更新后獲取的方差矩陣的預測值為:
(ζ(k+1|k)-x(k+1|k))T]+Q
(22)
根據測量方程對各個點進行非線性變換:
ζ(k+1|k)=h(ζ(k+1|k))
(23)
得到模型預測更新后的觀測值:
(24)
式中:r為測量噪聲的平均值。
2.1.5 測量更新過程
系統的輸出方差矩陣為:
(ζ(k+1|k)-z(k+1|k)T)]+R
(25)
協方差矩陣為:
(ζ(k+1|k)-z(k+1|k)T)]+R
(26)
卡爾曼濾波增益矩陣為:
(27)
對狀態進行更新后的濾波值為:
x(k+1|k+1)=x(k+1|k)+Ka(z(k+1)-
z(k+1|k))
(28)
后驗方差矩陣為:
P(k+1|k+1)=P(k+1|k)-
KaPzk+1zk+1KaT
(29)
2.2 自適應無跡卡爾曼濾波原理
在測量噪聲和過程噪聲為固定值的情況下,無跡卡爾曼濾波算法可完成車輛狀態參數估計。但實際上測量噪聲和過程噪聲具有不確定性。針對實際過程中噪聲的不確定性,提出基于Sage-Husa算法理論的自適應無跡卡爾曼濾波算法,該算法可對無跡卡爾曼濾波中的測量噪聲協方差和過程噪聲協方差進行實時修正。步驟如下:
(1) 按式(30)計算測量噪聲的估計平均值。
1|k)]
(30)
式中:bk+1=(1-d)/(1-dk+1);d為遺忘因子,取0.9。
(2) 按式(31)計算測量噪聲的估計協方差。
(31)
式中:ek+1為誤差,ek+1=z(k+1)-z(k+1|k)。
(3) 按式(32)計算過程噪聲的估計平均值。
qqk+1=(1-bk+1)qqk+bk+1[xk+1-
(32)
(4) 按式(33)計算測量噪聲的估計協方差。
RRk+1=(1-bk+1)RRk+bk+1(kak+1ek+1·
(33)
3 仿真驗證與分析
為驗證文中所建模型與自適應無跡卡爾曼濾波算法的正確性,建立Carsim和MATLAB/Simulink仿真平臺,聯合仿真結構見圖2。
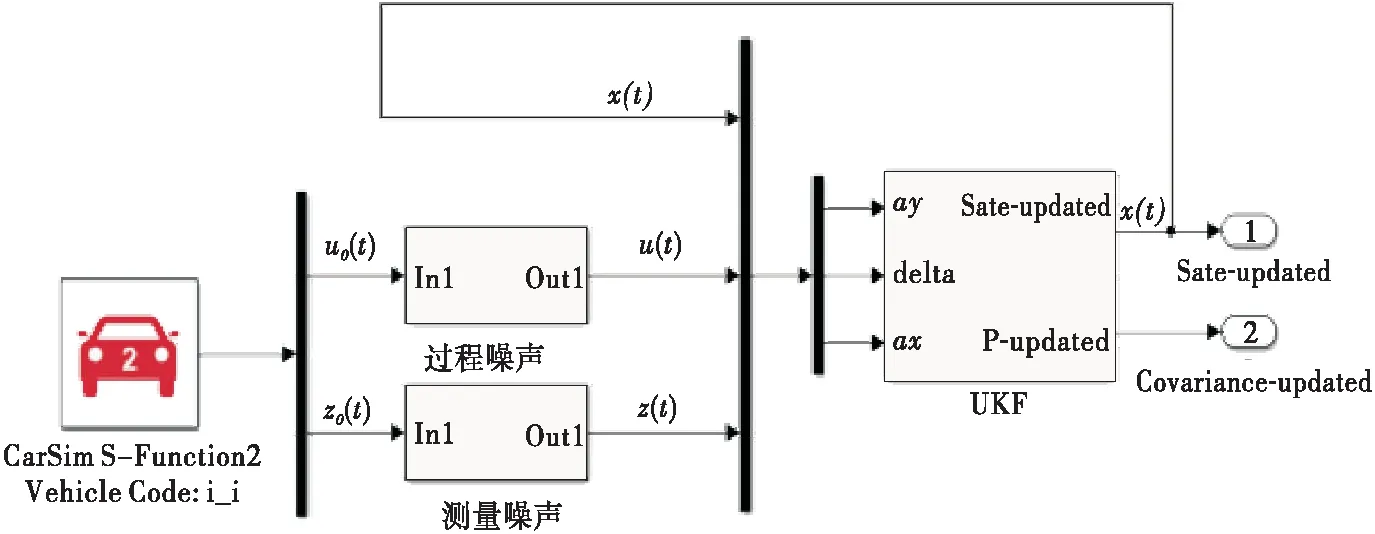
圖2 汽車狀態參數估計聯合仿真結構圖
仿真環境選取雙移線典型工況、附著系數為0.85的水平瀝青路面,仿真車輛選擇Carsim中自帶車輛,車速設置為72 km/h,采樣時間設置為0.01 s,整車質量m為1 500 kg,質心距前軸的距離a為1.55 m,軸距l為3.1 m,汽車繞z軸的轉動慣量為4 607.4 kg·m2,前輪總側偏剛度為-264 570 N/rad,后輪總側偏剛度為-240 000 N/rad。仿真工況控制輸入量見圖3~5。

圖3 雙移線工況下車輛輸出側向加速度
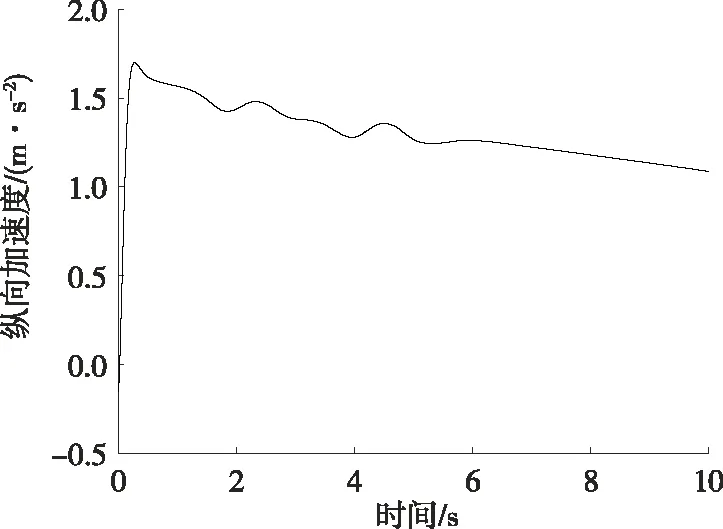
圖4 雙移線工況下車輛輸出縱向加速度
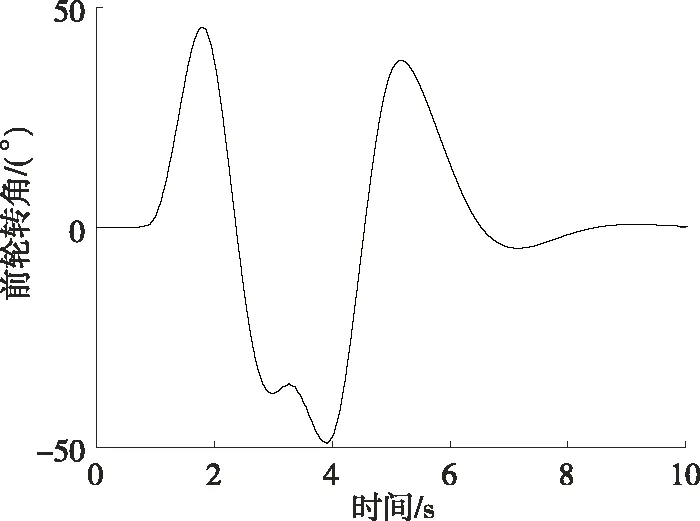
圖5 雙移線工況下車輛輸出前輪轉角
把車輛輸出的控制量和觀測量輸入UKF算法模型中,對3個狀態量進行實時估計。以Carsim軟件中車輛輸出的狀態量結果作為虛擬試驗值,將AUKF算法估計的狀態量結果與虛擬試驗值進行對比,驗證AUKF算法的正確性。AUKF算法估計求解結果、UKF算法估計求解結果與虛擬試驗值對比見圖6~8。
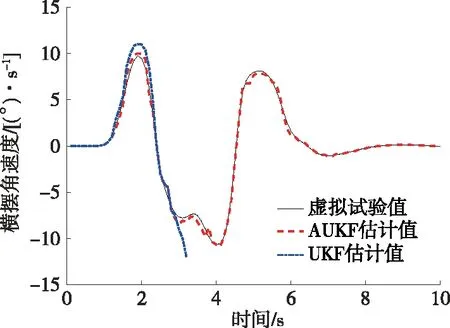
圖6 不同算法的橫擺角速度估計值對比

圖7 不同算法的質心側偏角估計值對比

圖8 不同算法的縱向速度估計值對比
由圖6可知:采用UKF算法對橫擺角速度進行估計時出現發散狀態,表明在應對不同噪聲時,UKF算法不能準確估計相應的狀態參數;而AUKF算法對橫擺角速度的估計值與虛擬試驗值較接近,兩者最大瞬態誤差為0.5 (°)/s,相對誤差僅5.101%,估計效果較理想。
由圖7可知:采用UKF算法對質心側偏角進行估計時出現發散狀態;而AUKF算法對質心側偏角的估計值與虛擬試驗值接近,最大瞬態誤差僅為0.04°,相對誤差為3.633%。
由圖8可知:采用UKF算法對縱向速度進行估計時出現發散狀態;而AUKF算法對縱向速度的估計值與虛擬試驗值接近,最大瞬態誤差為1.875 km/h,相對誤差僅為1.704%。
綜上,采用AUKF算法對汽車狀態參數進行估計的效果較好。
4 結語
采用自適應無跡卡爾曼濾波算法對汽車橫擺角速度、質心側偏角和縱向速度進行估計,結果表明該算法在車輛行駛環境中的噪聲發生變化時仍可對相應狀態參數進行估計,且估計精度較高。

