不同開挖方法下炭質板巖隧道圍巖穩定性及結構可靠度分析*

晉婉晴， 陳潔金， 胡敏

(長沙理工大學 土木工程學院， 湖南 長沙 410114)

海巴洛隧道是云南省香格里拉至麗江高速公路的重點控制性工程，所在地區地質構造復雜，揭露圍巖主要為強、全風化炭質板巖，薄層狀結構，節理裂隙、地下水一般發育。圍巖強度較低、水理性質較差，遇水易軟化、崩解，自穩能力極差，易受擾動。適用于炭質板巖隧道的施工方法有臺階法、三臺階預留核心土法、CD法和中導洞法等，這些方法各有優缺點。以該隧道的地質環境條件為主要依據，同時考慮其斷面尺寸、施工技術水平、造價及工期等，進口段選取施工速度快、工序簡單的臺階法施工，若開挖段較軟弱，可預留核心土來保證開挖掌子面的穩定性。該文采用有限元軟件建立三維模型，分析左線進口段采用臺階法與三臺階預留核心土法施工的過程，對比分析2種施工方法下圍巖位移、塑性區及襯砌結構內力。

目前隧道襯砌結構可靠度計算方法有一次二階矩法、隨機有限元法、蒙特卡洛法、響應面法等。其中矩法的高度非線性的功能函數很難處理，且精度不高，有一定誤差；響應面法和隨機有限元法需編制特定的程序，比較復雜。而蒙特卡洛法不會受非正態分布隨機變量及非線性功能函數的限制，相對于其他方法，只要模擬次數夠多，就是一種較精確的方法。而且MATLAB可實現蒙特卡洛直接抽樣法編程，不受復雜編程和算法的困擾。因此，依據有限元模擬所得襯砌結構的軸力與彎矩，采用MATLAB編寫蒙特卡洛直接抽樣法程序，計算在抗壓、受拉開裂條件下二次襯砌結構的可靠度。

1 基本原理及方法

1.1 隧道襯砌結構的極限方程

襯砌截面的破壞可作為建立隧道襯砌結構極限狀態方程的依據，但襯砌截面的破壞由襯砌強度決定，可能出現壓碎或拉裂2種不同的破壞形式。因此，根據襯砌截面抗壓和抗拉檢算式分別建立襯砌截面抗壓極限狀態方程和抗拉極限狀態方程。

當偏心矩eo≤ 0.2h時，將截面抗壓強度條件視為承載能力極限，功能函數為：

g1(x)=N極限-N=KRαbhRa-N

(1)

式中：N極限為襯砌砼能承受的極限軸力，即結構抗力；N為數值模擬求出的截面軸力，即作用效應；KR為抗力項的計算模式不定性；α為偏心影響系數；b為截面縱向寬度，取1 m；h為截面厚度；Ra為砼抗壓強度。

當偏心矩eo> 0.2h時，將截面受拉開裂條件視為承載能力極限，功能函數為：

(2)

式中：Rl為砼抗拉極限強度；Ks為荷載項的計算模式不定性；M為數值模擬求出的截面彎矩。

1.2 蒙特卡洛法基本原理與MATLAB實現

蒙特卡洛法又稱隨機抽樣法，主要包括直接抽樣法、重要抽樣法等，較適用于計算隧道襯砌結構可靠度。MATLAB是優秀的商業數學軟件，可實現蒙特卡洛直接抽樣法編程。該軟件提供了多種分布類型的隨機變量發生器，不必復雜地編程，就可生成實際工程中所需分布類型的隨機數，直接產生變量xi，然后代入功能函數進行計算，極大提高了運算效率，也使蒙特卡洛法在工程中應用更廣泛。基于蒙特卡洛法與MATLAB計算隧道襯砌結構可靠度的步驟與方法參考文獻[8-10]。文中用到的隨機變量生成隨機數的指令為r=normrnd(Mu,Sigma,m,n),表示產生服從N(μ,σ2)分布的m行n列隨機變量數組r。

基本思路：先把功能函數g(x1,x2,…,xi)中的各隨機變量xi(i=1,2,…,n)進行大量隨機抽樣，然后用這些隨機抽樣值生成函數產生m×n組隨機變量數組，將這些數組代入功能函數，統計其結果小于零的個數K，則失效概率Pf=K/(m×n)，可靠度指標β=-φ-1(Pf)。

2 隧道現場監控量測

海巴洛隧道左幅進口段ZK66+307斷面開挖寬度為12.5 m，高度為10.2 m，埋深為195 m。采用復合式襯砌，初期支護采用厚度為25 cm 的C25噴射砼、間距為60 cm的H200×200鋼拱架，二次襯砌采用厚度為50 cm的C30模筑鋼筋砼。采用臺階法開挖，下臺階開挖落后上臺階約10 m，二次襯砌施作落后下臺階開挖15 m，開挖進尺為1.6 m/d。

選取ZK66+307斷面對洞身水平收斂和拱頂沉降進行監測，監測結果圖1、圖 2。結合現場施工分析，第8 d上臺階開挖完畢，此時拱頂沉降為56 mm，水平收斂為26 mm；之后下臺階開挖，從13 d起變形增加量逐漸減緩；到21 d時，拱頂沉降達到84 mm，水平收斂為44 mm，圍巖變形趨于平穩。可見，臺階法施工的位移量在上臺階施工時變化速率最快，隨著下臺階開挖完成，二次襯砌及時閉環，拱頂沉降及水平收斂得到抑制，位移增速逐漸減緩，變形趨于穩定。

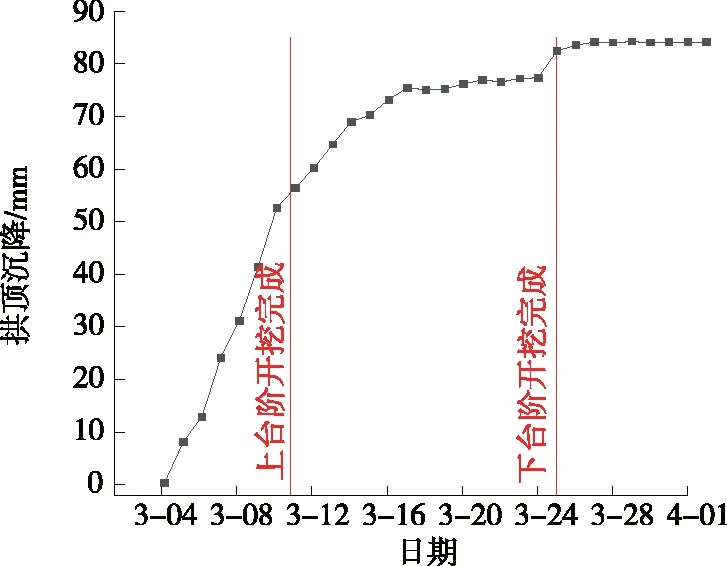
圖1 隧道斷面拱頂沉降曲線

圖2 隧道斷面洞身水平收斂曲線

3 隧道數值模擬及支護結構可靠度計算

3.1 建立隧道開挖支護模型

根據海巴洛隧道的開挖方法及支護方式，采用MIDAS GTS/NX進行三維數值分析。計算模型尺寸選取3～5倍洞徑，隧道橫向(x方向)取120 m，沿洞軸(y方向)長度取30 m，上下邊界(z方向)長度取100 m，隧道埋深取50m，上覆剩余土體自重通過在上表面施加2.9 MPa豎向壓力來模擬。模型底部固定約束，側面法向約束，上表面設為自由邊界，并施加等效荷載(見圖3)。

圖3 隧道三維數值模擬模型

圍巖為薄層炭質板巖，比起摩爾-庫倫準則，更適合采用廣義Hoek-Brown強度準則。Hoek-Brown強度準則確定了巖石發生屈服破壞時的應力關系式，可較好地反映巖體的非線性破壞特征，其應力關系式中的巖石參數可較好地反映由于層理面、結構面的存在引起的圍巖強度降低，較適用于節理裂隙發育巖體。該強度準則針對原有準則中的不足，在缺少現場試驗數據的情況下，根據大量工程經驗引入2個相關系數，可準確估計各類巖體的力學性質，更好地描述巖體軟硬程度及完整性。根據既有地質強度指標表，結合隧道揭露圍巖地質水文條件，確定地質強度指標GSI的取值為50、板巖巖石類型mi的取值為9、擾動參數D的取值為0.5。輸入參數可由有限元軟件自動算出mb(巖石的材料常數，反映巖石的堅硬程度)、s(Hoek-Brown經驗參數，反映巖體的破碎程度)、a(巖石的材料常數)。

圍巖采用各向同性的廣義Hoek-Brown本構模型，初期支護、錨桿和二次襯砌采用各向同性的彈性本構模型模擬。采用Solid單元模擬圍巖作用；支護結構參數采用等效法予以考慮，將鋼拱架的彈性模量折算至初期支護噴射砼；采用Shell單元模擬初期支護、二次襯砌的作用，并用彈性連接模擬其復合襯砌結構的作用。模擬計算參數見表1。

表1 數值模擬計算參數

3.2 隧道施工方法模擬

該隧道進口段圍巖級別為Ⅳ級，受開挖施工方法影響較大。模擬臺階法和三臺階預留核心土法的施工過程，對2種工法下隧道圍巖穩定性進行比較分析，模擬模型見圖4、圖5。

圖4 臺階法數值模擬模型

圖5 三臺階預留核心土法數值模擬模型

臺階法的模擬施工步驟：1) 開挖上臺階并施作初期支護及錨桿，上臺階高6 m、長6 m；2) 開挖下臺階并施作初期支護及錨桿，下臺階高4 m，及時施作仰拱；3) 隧道開挖完成，進行仰拱回填，施作二次襯砌(落后下臺階15 m)。循環進尺為2 m，每步開挖完成及時施作對應部位的初期支護及錨桿，應力一次釋放，施工階段以隧道部分全部開挖完成為止。

三臺階預留核心土法的模擬施工步驟：1) 上臺階開挖，預留核心土，及時施作初期支護及錨桿，上臺階高5 m、長4 m，核心土每2 m開挖一次；2) 錯開開挖核心土及中臺階，并施作邊墻初期支護及錨桿，中臺階高度2.5 m、長4 m；3) 開挖下臺階并施作初期支護及錨桿，下臺階高2.5 m；4) 隧道開挖完成，進行仰拱回填，施作二次襯砌(落后下臺階15 m)。循環進尺為2 m，每步開挖完成及時施作對應部位的初期支護及錨桿，應力一次釋放，施工階段以隧道部分全部開挖完成為止。

3.3 數值模擬結果分析

3.3.1 圍巖位移分析

圖6、圖7分別為臺階法、三臺階預留核心土法施工時圍巖總豎向位移和水平位移。由圖6、圖7可知：采用臺階法、三臺階預留核心土法施工時，施工完成后，拱部沉降較大，分別為0.076、0.065 m；仰拱的隆起值最大，分別為0.072、0.064 m；水平收斂最大值位于邊墻中下處，分別為0.040、0.038 m。

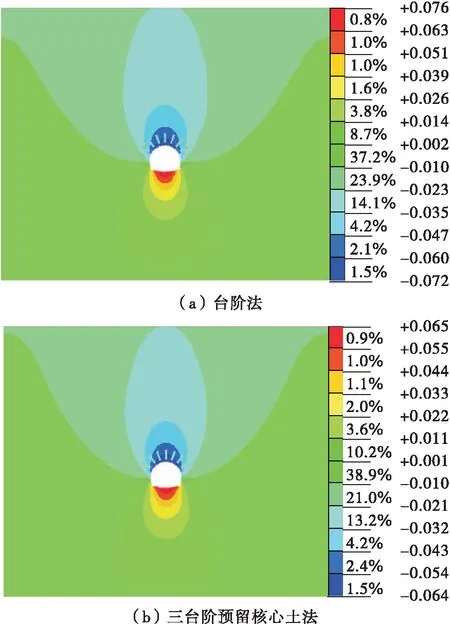
圖6 不同開挖方法下圍巖總豎向位移云圖(單位：m)

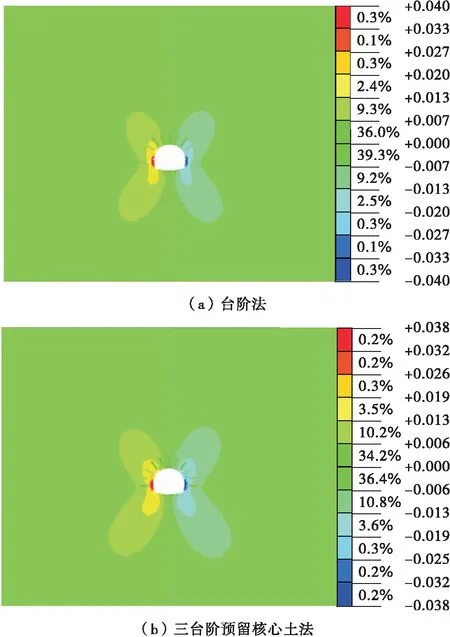
圖7 不同開挖方法下總水平位移云圖(單位：m)

取y=10 m處斷面為監測斷面，考慮2種施工方法下分部開挖的每階段拱頂沉降，研究整個施工過程中拱頂下沉值。圖8為該斷面拱頂下沉曲線。由圖8可知：僅上臺階開挖時，臺階法拱頂沉降為0.041 m，占開挖過程總沉降的59.3%；三臺階預留核心土法上臺階開挖時，拱頂沉降為0.033 m，占總沉降的53.2%；隨著下臺階開挖完成，沉降增幅逐漸減小；之后二次襯砌開始施作，沉降幾乎不再增長，漸漸趨于穩定。拱頂沉降主要發生在上臺階開挖。

圖8 隧道斷面拱頂沉降曲線

對比臺階法模擬的圍巖位移變化結果與現場監控量測結果，其變化規律相同，最終位移值也較吻合；模擬沉降值和水平收斂值偏小，這是由于模擬過程中省略簡化較多，如未考慮水的作用。但總體相差較小，證明了數值模擬的準確性。

臺階法的總豎向位移及總水平收斂大于三臺階預留核心土法，這是由于隧道開挖段的圍巖是薄層板巖，較軟弱，采用預留核心土法相當于減小了每次隧道開挖掌子面的開挖面積，上臺階開挖時對圍巖的擾動減小了很多，可增強掌子面的穩定性，并縮短臺階間的開挖步距，加上及時進行初期支護，更能有效控制圍巖位移。

3.3.2 圍巖塑性區分析

圖9為臺階法、三臺階預留核心土法施工時圍巖有效塑性應變。

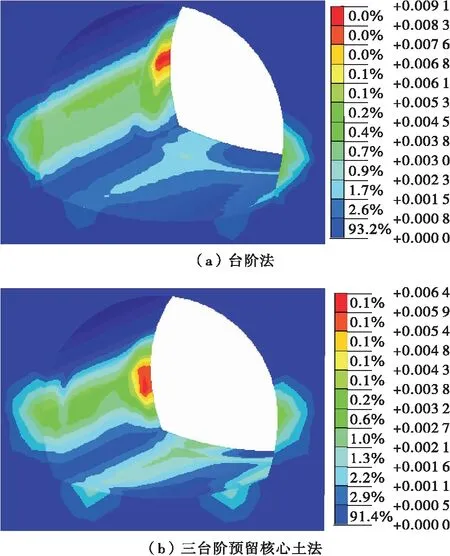
圖9 不同開挖方法下圍巖有效塑性應變云圖

由圖9可知：隧道施工完成后，2種方法施工時的塑性區均發生在拱腳附近及臺階開挖銜接處，且塑性應變最大值出現在臺階開挖銜接處，分別為0.009 1、0.006 4。說明這些部位屬于薄弱部位，較易發生破壞，應重點關注，加強監測，及時支護，必要時采取加固措施。三臺階預留核心土法的有效塑性應變值比臺階法的小，主要是因為其臺階長度比臺階法短，可快速有效地施作初期支護，圍巖直接暴露在外的時間短，更有利于圍巖的穩定。

3.3.3 二次襯砌結構內力

取y=10 m處斷面作為監測斷面，分別提取拱頂、拱腳、拱腰和拱底位置二次襯砌的軸力、彎矩，結果見表2。

表2 襯砌結構重點部位的內力值

由表2可知：由于施工步驟不同，2種施工方法下結構內力最大值出現的部位存在差異，但臺階法結構內力值始終較大，相比三臺階預留核心土法，臺階法施工時二次襯砌結構更容易達到極限強度，也就更容易發生破壞。

綜上，對比圍巖位移、應力及二次襯砌結構內力，三臺階預留核心土法施工對海巴洛隧道進口段圍巖的擾動更小，施工過程中圍巖變形、二次襯砌結構內力較小，更適合該隧道。

3.4 隧道支護結構可靠度計算

針對隧道襯砌結構分別按抗壓、抗裂條件要求建立功能函數[見式(1)、式(2)]，KR、Ks、Ra、Rl、h根據文獻[13]取值，其統計特征見表3。

表3 基本隨機變量的統計特征值

利用MATLAB編寫蒙特卡洛直接抽樣法程序，將表3中隨機變量值代入功能函數，然后將有限元模擬求得的二次襯砌結構軸力和彎矩輸入MATLAB程序，采用蒙特卡洛法進行100萬次直接抽樣，求得支護結構可靠度(見表4)。

表4 不同開挖方法下襯砌結構可靠度計算結果

根據文獻[14]提出的隧道襯砌承載能力極限狀態目標可靠度指標，安全等級為二級時目標可靠度指標為4.2，安全等級為一級或三級時目標可靠度指標相應提高或降低0.5。與表3對比，三臺階預留核心土法施工的二次襯砌結構可靠度指標均滿足要求。在相同支護參數條件下，三臺階預留核心土法由于每階段的開挖面積較小，對圍巖的擾動較小，增強了掌子面的穩定性，引起的圍巖位移及應力較小，二次襯砌結構更穩定。

4 結論

采用MIDAS GTS/NX建立三維數值模型，模擬臺階法與三臺階預留核心土法的施工過程，分析2種施工方法下圍巖位移和塑性區及二次襯砌結構內力，并利用MATLAB編寫蒙特卡洛直接抽樣法程序，計算2種施工方法下襯砌結構在抗壓、抗裂條件下的可靠度。得出以下結論：

(1) 海巴洛隧道開挖施工過程模擬結果與現場實測數據相差不大，變化規律一致。其拱頂沉降主要發生在上臺階開挖階段，減小上臺階開挖對隧道的擾動可有效減小圍巖變形。

(2) 對于海巴洛炭質板巖隧道，采用三臺階預留核心土法施工時拱頂沉降和仰拱隆起值均小于臺階法開挖，預留核心土法更能有效控制圍巖位移。

(3) 2種施工方法下，隧道圍巖塑性區均發生在臺階開挖銜接處及拱腳附近，說明這些部位較脆弱，施工時必須及時支護，實時監測，必要時采取加固措施。

(4) 在相同支護參數下，采用三臺階預留核心土法施工時二次襯砌結構的可靠度滿足規范要求，襯砌結構不易破壞，可獲得較穩定的隧道整體結構。