基于優(yōu)化卷積神經(jīng)網(wǎng)絡的建筑工程造價估算

王淑蘋，黃良輝

(1.廣東南華工商職業(yè)學院 建筑與藝術設計學院，廣東 廣州 510507；2.廣東建設職業(yè)技術學院，廣東 廣州 510440)

0 引言

近幾年來隨著市場競爭的不斷加劇，建筑企業(yè)的利潤不斷降低，成本控制已經(jīng)成為了建筑企業(yè)未來發(fā)展的核心，因此建筑工程造價的估算具有重要意義。傳統(tǒng)的建筑工程造價估算主要采用回歸模型和蒙特卡羅模擬估算模型[1-4]，這些方法存在計算精度較低和耗費時間較長的缺陷。

如今，隨著人工智能技術的發(fā)展，研究人員開始將人工神經(jīng)網(wǎng)絡、模糊數(shù)學和灰色系統(tǒng)等技術應用于工程造價估算領域。例如，孟俊娜等人[5]提出基于BP神經(jīng)網(wǎng)絡的民用建筑工程造價估算方法，通過提取相應的工程特征指標，以工程造價作為輸出值，驗證了BP神經(jīng)網(wǎng)絡模型的可行性。劉春[6]提出了一種基于改進布谷鳥搜索算法優(yōu)化支持向量機的建筑工程造價估算模型，通過改進布谷鳥搜索算法估計支持向量機參數(shù)，從而提高了工程造價估算準確性，但是其造價估算指標體系選取數(shù)量較少，且支持向量機參數(shù)優(yōu)化的效果不突出[7-9]，即局部尋優(yōu)和全局尋優(yōu)之間的平衡較為困難，直接限制了估算的最小誤差性能[10]。通過分析發(fā)現(xiàn)上述模型的準確率仍無法滿足實際工程管理需求。

隨著深度學習理論的提出和硬件設備計算性能的提升，卷積神經(jīng)網(wǎng)絡以更高的識別率在計算機視覺和自然語言處理領域獲得了極大的成功[11-13]。因此，本文嘗試將卷積神經(jīng)網(wǎng)絡引入到建筑工程造價估算應用中，以便進一步提高造價估算的準確性。通過100個實際住宅樓案例工程的驗證分析，驗證了狼群優(yōu)化的卷積神經(jīng)網(wǎng)絡模型的有效性。

1 建筑工程造價估算指標體系構建

建筑工程項目建設周期長，影響因素復雜。但是，不可能選取所有影響建筑工程造價的因子。因此，在整個建筑工程的建設周期內，需要合理選擇影響建筑工程造價最密切的因子。在查閱大量的工程造價相關資料后，歸納出13項對工程造價影響較大的因子，如表1所示。

表1 建筑工程造價估算指標體系

其中，工程造價指數(shù)是造價報告期和基期的比值，本文以廣州市住宅樓為研究對象。鋼筋均價變化率和混凝土均價變化率都是按照2018年廣州市的基準價來衡量的。單方造價指標以“元/m2”為單位進行量化。

2 基于卷積神經(jīng)網(wǎng)絡的建筑工程造價估算模型建立

2.1 確定輸入序列

由于建設地點、工程開/竣工時間估算指標會大大增加卷積神經(jīng)網(wǎng)絡模型的冗余結構，而且考慮到僅針對廣州地區(qū)近幾年的住宅樓數(shù)據(jù)，因此去除了上述2個指標因子，保留其余11個。對于n個代表性的住宅樓樣本，根據(jù)上述構建的建筑工程造價估算指標體系，設置11個指標因子作為輸入序列，如表2所示。

可以看出，表2中包含了2類指標：定量和定性。例如結構類型X10和建筑外形X11為定性指標，其余都是定量指標。結構類型X10中框架剪力墻、剪力墻和框架分別對應-1、0、1，建筑外形X11也類似設置。

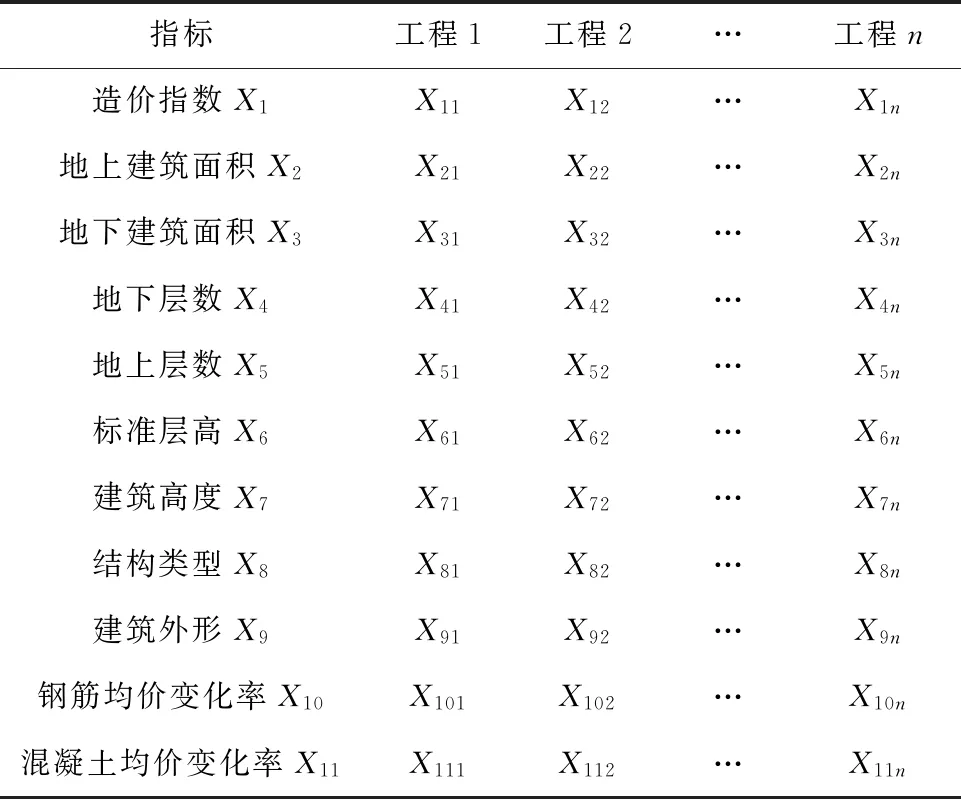
表2 住宅樓估算指標輸入序列

2.2 數(shù)據(jù)歸一化處理

在將估算指標輸入序列輸入到卷積神經(jīng)網(wǎng)絡之前，必須將其進行歸一化處理，從而實現(xiàn)量綱一致。對于表2中的定量指標，具體為式(1)。

(1)

其中，Xmax表示輸入序列的最大值；Xmin則表示最小值。

2.3 卷積神經(jīng)網(wǎng)絡模型生成

在上述歸一化后，建筑工程造價估算指標輸入序列的樣本集為X=(x1,x2,…xn)，n個樣本通過第l層的卷積和轉換運算如式(2)。

(2)

其中，wji和Bl分別表示l層的神經(jīng)元i與第j個輸入對應的卷積核及偏置，f(·)的表達式為式(3)。

(3)

卷積核主要包含n個樣本的m個特征卷積池化操作，設卷積核尺寸為h×w，池化方法有2種[14]，分別為式(4)、式(5)。

(4)

(5)

選擇式(5)的池化方法，令M=n/(h×w)，樣本X=(x1,x2,…，xn)卷積池化后重新得到的樣本為式(6)。

X=(x1,x2,…，xM)

(6)

然后根據(jù)卷積池化后的樣本按照式(2)進行轉換運算。

設輸出層的第k個節(jié)點預測輸出為yk，實際輸出為dk，則誤差項δk為式(7)。

δk=(dk-yk)yk(1-yk)

(7)

卷積神經(jīng)網(wǎng)絡訓練的所有節(jié)點誤差函數(shù)為式(8)。

(8)

2.4 網(wǎng)絡參數(shù)的狼群優(yōu)化

可以按照式(7)和梯度遞減方法不斷的迭代求取最優(yōu)權重和偏置，以便尋得最優(yōu)的網(wǎng)絡連接，但是這種方式效率十分低下。實際應用中主要依靠經(jīng)驗指導進行調參，這過于依賴專家的專業(yè)水平。

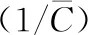
(9)

其中，Ci表示第i個工程的造價估算誤差。

設頭狼為P=[p1,p2,…,pN]，N為權重和偏置總數(shù)，狼群中總狼數(shù)量為M，其他M-1只狼的坐標集合為Q，其中某一只狼的坐標為Qi=[qi1,qi2,…，qiN]，i=1,2,…,N-1。

從Q選取部分樣本作為方向狼，即它們的設方向狼數(shù)量為Tnum，其移動方式為式(10)。

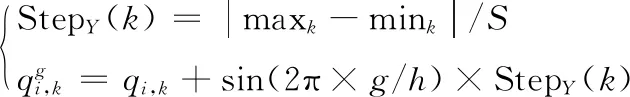
(10)

其中，S和h分別表示權重值和移動方向。i=1,2,…,Tnum，g=1,2,…,h。

那么在頭狼的引導下，其他狼的移動方式為式(11)。

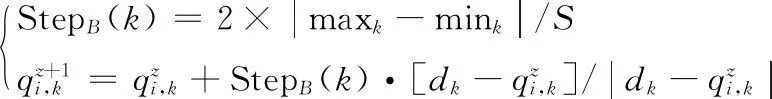
(11)

其中，i=1,2,…,N-Tnum-1。dk表示其他狼與頭狼的距離值，且dk∈(0,Dk)，如式(12)。

(12)

最后非頭狼對獵物圍攻，移動方式為式(13)。

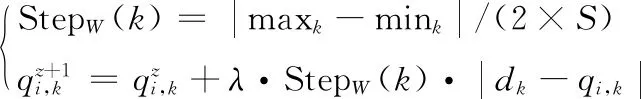
(13)

z=1,2,…,N-1，λ為[-1,1]內的隨機數(shù)。

2.5 建筑工程造價估算流程

采用狼群優(yōu)化卷積神經(jīng)網(wǎng)絡的建筑工程造價估算流程，如圖1所示。

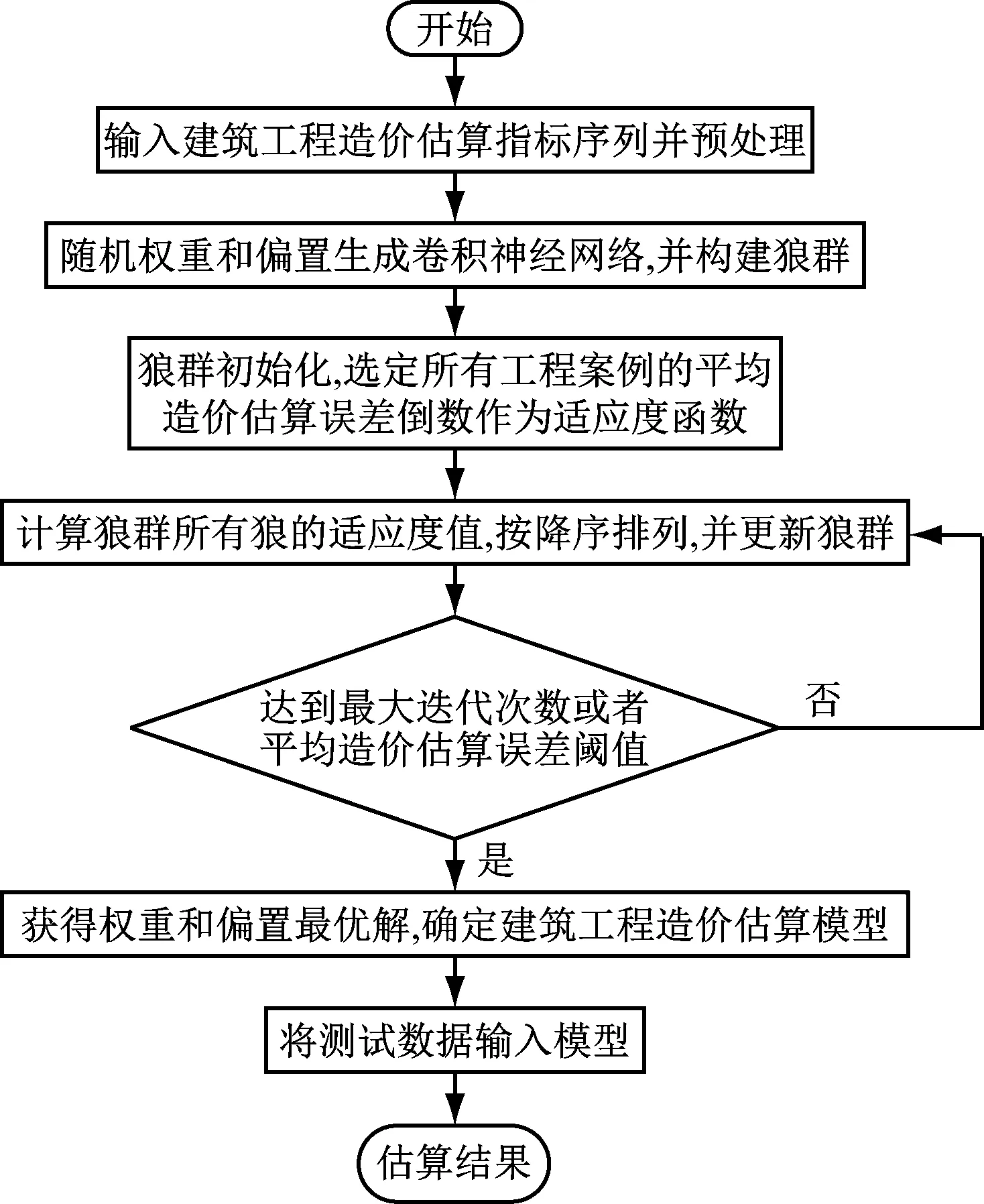
圖1 基于狼群優(yōu)化卷積神經(jīng)網(wǎng)絡的造價估算流程

3 實例分析

從國內某造價指標網(wǎng)站采集了2012-2016年廣州地區(qū)的100個高層住宅樓樣本，其中的90個作為優(yōu)化卷積神經(jīng)網(wǎng)絡造價估算模型的訓練樣本，其余10個作為測試樣本。在MATLAB平臺中運行該造價估算模型，卷積核尺寸為3×3，訓練次數(shù)為20次，訓練數(shù)據(jù)輸出曲線如圖2所示。

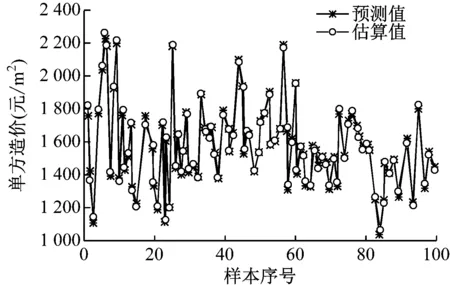
圖2 訓練數(shù)據(jù)輸出曲線

3.1 狼群優(yōu)化的影響分析

設置3×3卷積模式下，分別采用卷積神經(jīng)網(wǎng)絡模型和狼群優(yōu)化后模型進行樣本訓練和測試，以驗證狼群優(yōu)化的影響。訓練次數(shù)為20，選取96-100號測試樣本，2種模型的建筑工程造價估算性能如表3所示。

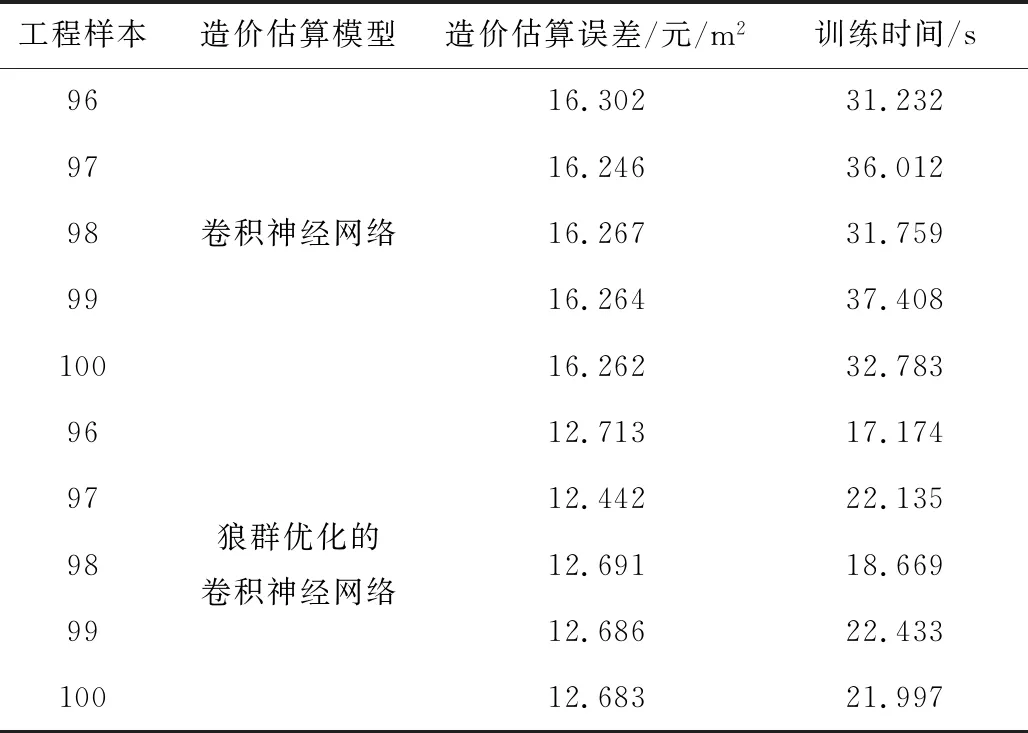
表3 2種模型的建筑工程造價估算性能

從表3可以看出，狼群算法優(yōu)化過的卷積神經(jīng)網(wǎng)絡，不論是在造價估算誤差尋優(yōu)還是在訓練時間方面，均表現(xiàn)出更優(yōu)異的性能。

3.2 不同模型的造價估算準確率對比

為了驗證不同模型的建筑工程造價估算性能，在相同實驗平臺中，分別采用BP神經(jīng)網(wǎng)絡模型、布谷鳥搜索支持向量機模型和本文模型對相同的90個樣本進行訓練。對于10個測試樣本，不同模型得到的預測值與實際值之間相對誤差對比如圖3所示。

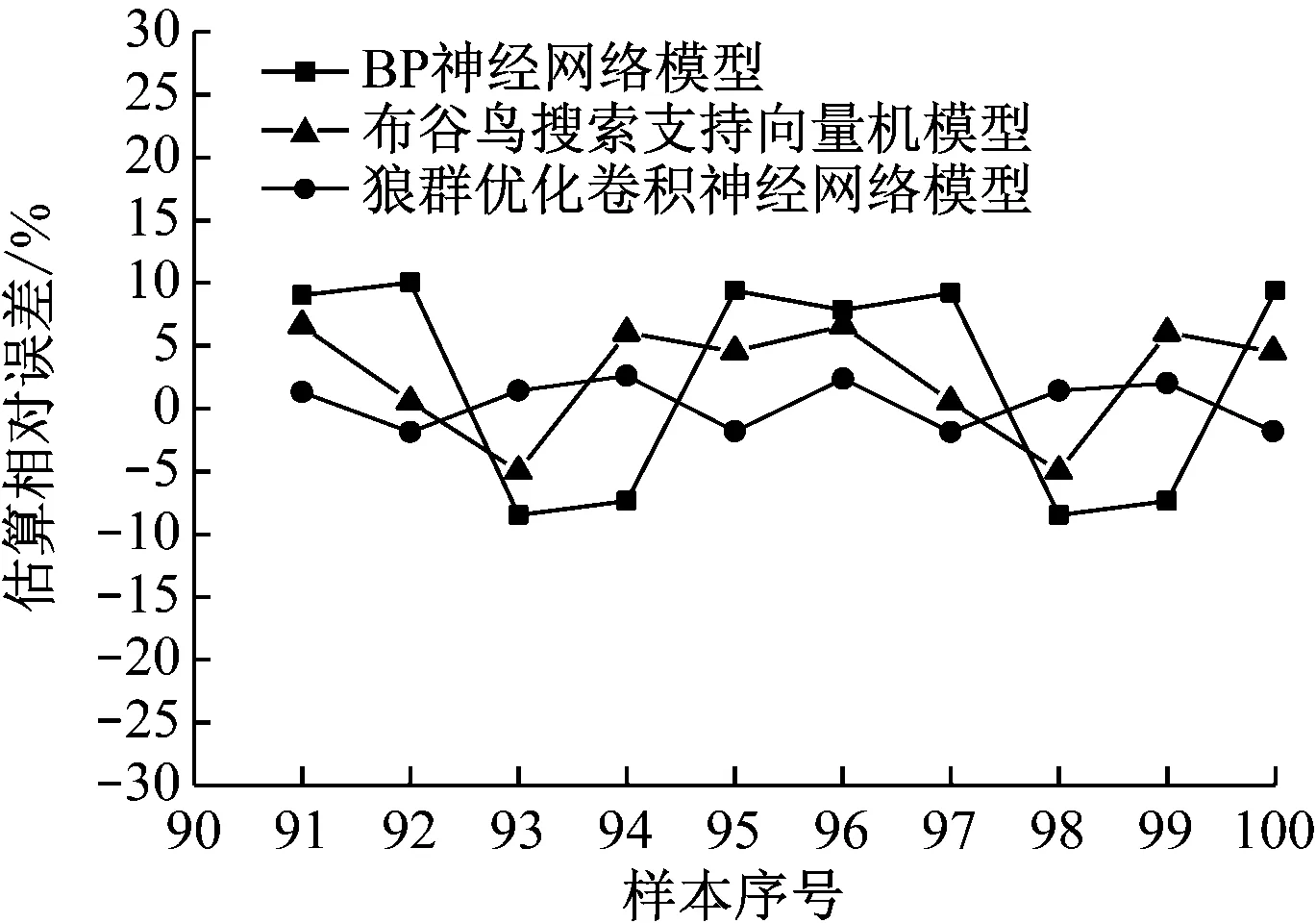
圖3 不同模型的估算相對誤差對比

從圖3可以看出，在建筑工程造價估算相對誤差方面，BP神經(jīng)網(wǎng)絡模型表現(xiàn)最差。在個別測試樣本上布谷鳥搜索支持向量機模型表現(xiàn)出了優(yōu)異性能，但是綜合所有5個測試樣本的結果而言，本文狼群優(yōu)化卷積神經(jīng)網(wǎng)絡模型求解單方造價的平均相對誤差最小，平均相對誤差僅為0.16%，布谷鳥搜索支持向量機模型次之，BP神經(jīng)網(wǎng)絡模型最差。

4 總結

本文采用狼群優(yōu)化的卷積神經(jīng)網(wǎng)絡模型對建筑工程造價進行估算。采用卷積神經(jīng)網(wǎng)絡構建了建筑工程造價估算模型，并采用狼群算法對權重和偏置進行優(yōu)化，以便在非經(jīng)驗指導下自動尋得最優(yōu)連接。通過100個實際住宅樓案例工程的驗證分析。結果表明，提出估算模型的平均相對誤差僅為0.16%，明顯優(yōu)于其他常用模型。后續(xù)研究將進一步優(yōu)化狼群算法參數(shù)，提高狼群優(yōu)化的卷積神經(jīng)網(wǎng)絡算法的收斂時間性能。