壺瓶碎米薺多糖提取動力學模型研究

張琴，李美東，張子木，黃秀芳，周毅峰，羅凱

(湖北民族大學 生物科學與技術學院，湖北 恩施，445000)

壺瓶碎米薺(Cardaminehupingshanensis)，又稱虎耳金，是十字花科碎米薺屬植物,性平、味苦，具有止咳平喘、活血等功效[1-2]。其幼嫩莖葉是一種珍稀的野菜，可作蔬菜食用。碎米薺中含有豐富的水分、蛋白質、可溶性糖、氨基酸、維生素C、纖維素以及硒[3]。其中恩施地區壺瓶碎米薺硒含量豐富,它的根、芽和葉中硒的平均含量分別可以達到2 985、3 329和2 491 mg/kg[4-5]。

植物中營養成分繁多，在提取不同成分時，有著比較復雜的傳質和傳熱過程[6-7]。部分植物多糖已經探索出了相關提取動力學模型[8-10]，但沒有普遍適用于所有植物多糖的提取動力學模型。目前壺瓶碎米薺多糖的研究主要在硒多糖提取、純化等過程的工藝優化和活性方面探究[11-13]，缺少從理論上探究其提取過程的相關研究。如何提高壺瓶碎米薺多糖的提取得率對開發、生產壺瓶碎米薺多糖相關產品的成本和經濟效益有很大影響。因此，建立一個可靠的壺瓶碎米薺多糖提取動力學模型是十分必要的。本文結合Fick第二擴散定律[14]對超聲提取壺瓶碎米薺多糖進行建模，采用超聲輔助提取壺瓶碎米薺多糖，同時, 從理論上探究壺瓶碎米薺多糖提取過程, 得到相應的提取動力學方程和相關參數，從而為壺瓶碎米薺多糖的提取提供理論依據和技術支撐。

1 材料與方法

1.1 材料與試劑

材料：壺瓶碎米薺購買于湖北恩施新塘鄉，55 ℃烘干后粉碎過100目篩備用。

試劑：無水乙醇、標準葡萄糖溶液、濃硫酸、苯酚等均為分析純。

1.2 儀器與設備

GZX-9246MBE 電熱鼓風干燥箱，上海博迅醫療生物儀器股份有限公司； LD-Y500A高速萬能粉碎機，上海頂帥電器有限公司； KQ-300DE 數控超聲波清洗儀，昆山市超聲儀器有限公司； UV-8000H 紫外-可見分光光度計，上海元析儀器有限公司；低速冷凍離心機，湖南湘儀實驗室儀器開發有限公司。

1.3 提取及檢測方法

1.3.1 壺瓶碎米薺多糖超聲提取

多糖的提取參考相關文獻[13],略有改動。將采購的壺瓶碎米薺用水洗凈后于55 ℃烘干，粉碎過100目篩， 在超聲輔助條件下進行提取然后通過離心、過濾、凍融、醇沉12 h，再次進行離心、過濾、干燥得到多糖粗品。在固液比1∶30的條件下，分別在超聲功率120、180、240和300 W 4個水平上進行處理。同時，提取溫度設為293、313、333、353K。所有試驗中，提取時間設為10、20、30、40、50、60、70和80 min 8個水平。所有試驗做3個平行處理。

1.3.2 多糖含量測定

壺瓶碎米薺多糖含量測定參考相關文獻[13, 15]進行。以葡萄糖標準品的質量濃度值(單位：mg/mL)為橫坐標(x)，吸光度值為縱坐標(y)，作標準曲線，計算得到方程為:y=10.405x+0.007 7(R2=0.999 1，質量濃度值為0～0.84 mg /mL時，質量濃度和吸光度值的線性關系良好)。吸取1 mL復溶后的樣液，置于試管中，加1 mL 6%(體積分數)苯酚溶液，混勻，再加入濃硫酸5 mL，搖勻，以相應試劑為空白管,同時進行 15 min的沸水浴，冷卻后在490 nm下測定吸光度。

1.4 壺瓶碎米薺多糖提取動力學模型建立

本試驗以壺瓶碎米薺為原料，以水為溶劑，分析、探究超聲提取壺瓶碎米薺多糖的提取動力學過程。壺瓶碎米薺多糖在提取過程中涉及到溶質的擴散理論[16]，在提取過程主要包括溶劑浸潤、內擴散和外擴散3個過程[17]。在提取過程中，壺瓶碎米薺粉末顆粒中的多糖含量在不斷減少，是一個非穩態的擴散過程。因此可以利用Fick第二定律研究壺瓶碎米薺多糖提取過程[18-19]。

假設：(1)壺瓶碎米薺粉碎成均勻的球型顆粒；(2)多糖的擴散是從球型顆粒內部沿著半徑方向進行的；(3)提取過程中，壺瓶碎米薺顆粒內部多糖的質量濃度不隨時間改變，擴散系數也不變，整個提取過程壺瓶碎米薺內部溫度一致；(4)不考慮多糖在壺瓶碎米薺顆粒表面的傳質阻力。其中，設定壺瓶碎米薺粉末半徑為R，顆粒內的溶劑體積為V1提取過程中，t時刻顆粒內距球表面為r處的有效成分質量濃度為C，D表示內擴散系數。C∞為平衡濃度，C0為初始濃度。

根據Fick第二定律：

(1)

假定壺瓶碎米薺為球型，滿足球對稱擴散。

(2)

令f=Cr邊界條件為：r=0,f=0，則：依據傅里葉變換得：

(3)

(4)

因為多糖的濃度分布是無窮極分布，其高次項趨近于零，可以忽略不計，因而當式(4)中n=1，令k=π2D/R2，則得到式(5)：

(C∞-C)/(C∞-C0)=(6/π2) exp(-kt)

(5)

將式(5)等號左側分子分母同時除以C∞，并兩邊同時被1除且兩邊取對數，則得到式(6)：

(6)

式(5)、(6)兩式為動力學模型，兩個式子都能表示出壺瓶碎米薺多糖粉末顆粒的半徑、提取的時間、溫度與多糖濃度之間的關系。

2 結果與分析

2.1 速率常數k的求解

2.1.1 不同溫度下速率常數k的求解

在240 W功率下進行不同溫度提取壺瓶碎米薺多糖。當提取壺瓶碎米薺多糖，得到的質量濃度維持穩態或者變化較小時，這時可認定己達到提取濃度平衡狀態，此時為平衡濃度。在同一功率條件下，影響多糖提取濃度的是多糖的擴散速度，影響其擴散速度的是溫度的大小。由表1可以看出溫度對壺瓶碎米薺多糖的提取濃度有影響：隨著溫度的升高，壺瓶碎米薺多糖的提取濃度增大；溫度越高，提取濃度達到平衡所需時間也越短。在240 W功率下，不同溫度提取壺瓶碎米薺多糖的平衡濃度如表2所示。

表1 不同溫度條件下提取壺瓶碎米薺多糖的質量濃度 單位：mg/mL

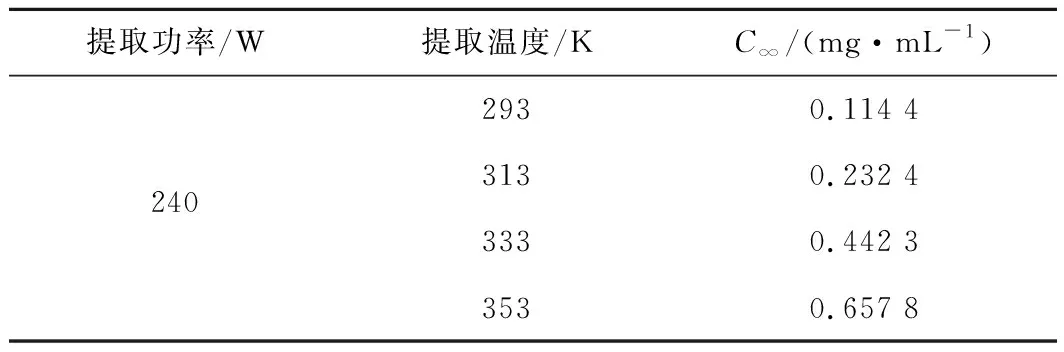
表2 不同溫度提取條件壺瓶碎米薺多糖的平衡濃度Table 2 Equilibrium concentration of Cardamine hupingshanensis polysaccharide under different extraction conditions

根據表1和表2的試驗數據作ln(C∞/C∞-C)與提取時間t的關系圖,結果見圖1。

圖1 240 W功率條件下不同溫度ln(C∞/C∞-C)與時間的關系Fig.1 Relationship between different temperatures ln(C∞/C∞-C) and extraction time at 240 W

由表1、表2和圖1得到的直線回歸方程的回歸結果和相應的表觀速率常數見表3。

表3 不同溫度對應的提取直線回歸結果Table 3 The result of extraction linear regression at different temperatures

從表1、表3和圖1 可以看出，由動力學模型和實驗數據推出的提取動力學方程式線性關系良好，其相關系數均在0.90以上。從表3可以得出在同一功率下，溫度在293～353K時隨著溫度的升高，表觀速率常數也在逐漸增大。說明溫度升高有利于加快壺瓶碎米薺多糖的溶出，提高多糖提取量。

2.1.2 不同超聲功率條件下速率常數k的求解

在353 K溫度下，利用不同超聲功率提取壺瓶碎米薺多糖，得到的多糖質量濃度如表4所示。

表4 不同功率下壺瓶碎米薺多糖質量濃度 單位：mg/mL

由表4可以看出，在同一溫度、時間條件下，功率越高，提取得到的多糖濃度越大。由表4可知353K溫度下進行不同功率提取壺瓶碎米薺多糖的平衡濃度，如表5所示。

表5 不同功率提取條件壺瓶碎米薺多糖的平衡濃度Table 5 Equilibrium concentration of Cardamine hupingshanensis polysaccharide under different extraction conditions

利用表4和表5 的實驗數據作ln(C∞/C∞-C)與提取時間t的關系圖,結果見圖2。由圖2得到的直線回歸方程的回歸結果和相應的表觀速率常數見表6。

圖2 353 K溫度條件下不同功率ln(C∞/C∞-C)與提取時間t的關系Fig.2 Relationship between different power ln (C∞/C ∞-C) and extraction time at 353 K

表6 不同功率對應的提取直線回歸結果Table 6 extracted linear regression results of different powers

從表4、表6和圖2，推導得到的提取動力學方程模型與測得的數據結果擬合所得的方程線性關系良好，其相關系數均在0.92以上。由表6 可以看出，在同一溫度下，隨著功率的升高,表觀速率常數逐漸增大，說明升高超聲提取的功率有利于加快壺瓶碎米薺多糖的溶出，提高多糖得率。

2.2 相對萃余率的求解

壺瓶碎米薺粉末顆粒加入水中0 min時,這時C0=0，由此可設定相對萃余率Y=(C∞-C)/C∞，則公式(5)可以變換為Y=(6/π2)exp(-kt)，以Y為縱坐標，提取時間t為橫坐標作相對萃余率Y=(C∞-C)/C∞對提取時間t關系圖。

2.2.1 不同溫度下相對萃余率的求解

由表1、表2實驗數據作在同一功率下不同溫度相對萃余率Y=(C∞-C)/C∞對提取時間t關系圖。由圖3擬合得到的回歸方程和對應的速率常數分別見表7。

圖3 240 W超聲不同溫度下萃余率與時間的關系Fig.3 Relationship between extraction recovery and time at different temperatures under 240 W ultrasound

表7 不同溫度下多糖相對萃余率對時間回歸結果Table 7 Time regression results of relative extraction rate of polysaccharides at different temperatures

由圖3和表7 可以看出，在相同功率不同溫度下提取多糖的過程中關于相對萃余率Y=(C∞-C)/C∞對提取時間t擬合方程,相關系數R2均在0.90以上，曲線擬合度良好。表明提取壺瓶碎米薺多糖的過程符合指數模型。由表7擬合所得方程可知，時間越長，萃余率越小；且在功率240 W下，溫度越高，多糖萃余率越小，則提取率(1-Y)隨著溫度升高而增大。反映出溫度為293～353 K時，升高溫度可以加快多糖提取。

2.2.2 不同功率下相對萃余率的求解

由表4、表5實驗數據作在同一溫度下不同時間相對萃余率Y=(C∞-C)/C∞對提取時間t關系圖。結果如圖4所示。由圖4擬合得到的回歸方程和對應的速率常數見表8。

由圖4和表8可以看出，在相同溫度不同得超聲功率下提取多糖的過程中關于相對萃余率Y=(C∞-C)/C∞對提取時間t擬合方程相關系數R2均在0.92以上，曲線擬合精度良好，表明壺瓶碎米薺多糖的提取過程符合指數模型。由表8擬合所得方程可知，隨著時間的延長，萃余率減小；溫度353 K下，功率越高，多糖萃余率越小，則提取率(1-Y)增大，反映出功率的增加可以加快多糖的提取。說明超聲破壞了細胞，加大了多糖的溶出通道，從而加快多糖的溶出。

圖4 353 K下不同功率下萃余率與時間的關系Fig.4 Relationship between recovery and time at different power at 353 K

表8 不同功率下多糖相對萃余率對時間回歸結果Table 8 Regression results of relative extraction rate of polysaccharide to time under different power

2.3 壺瓶碎米薺多糖提取活化能的求解

阿倫尼烏斯公式是由瑞典的阿倫尼烏斯所創立的[20]。它是化學反應速率常數隨溫度變化關系的經驗公式，公式寫作k=Aexp(-Ea/RT)。k是2.1求得的速率常數，R是摩爾氣體常量等于8.314 J/(mol·K)，T為溫度，Ea代表活化能，A為頻率因子。

將上述公式轉換為lnk=lnA-(Ea/RT)。利用表3中的數據對lnk和1/T作(圖5)，斜率為-Ea/R。

圖5 壺瓶碎米薺多糖提取lnk與1/T的關系圖Fig.5 Relationship between lnk and 1/T of Cardamine hupingshanensis polysaccharide extraction

由圖5可以看出，240 W時，lnk和1/T關系曲線的擬合方程為lnk=-1 005.2(-Ea/R)-0.120 5,R2=0.908 5,在240 W時lnk和1/T具有良好的相關性，但相關系數未達到0.95以上，推測導致這一問題的原因可能是超聲儀器的控溫系統不夠穩定，溫度不能保持恒定不變。根據回歸方程可以計算得到240 W功率下壺瓶碎米薺多糖提取過程中的活化能Ea為8 357.232 8 J/mol。

2.4 半衰期的求解

t1/2是指提取了平衡濃度一半時所經歷的時間[21]，所以這時C=C∞/2。根據式(6)可推論出t1/2=[ln2-ln(π2/6)]/k，約為t1/2=ln1.215 8/k。由表4、表6 所提供的k值可以求出t1/2,以t1/2為縱坐標,橫坐標是提取多糖的溫度T作圖，得到圖6，以t1/2為縱坐標,以提取多糖的超聲功率P作圖，得到圖7。

圖6 t1/2 與溫度的關系圖Fig.6 Relationship between t1/2 and temperature

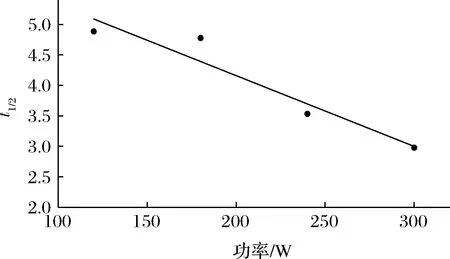
圖7 t1/2 與功率的關系圖Fig.7 Relationship between t1/2and work and power

由圖6、圖7可以得出，353 K時t1/2與功率P關系曲線的擬合方程為t1/2=-0.011 6P-6.480 8，R2=0.917 9。240 W時，t1/2和溫度關系曲線的擬合方程為t1/2=-0.048 2P+20.71，R2=0.966 9。

由此可知在同一超聲功率下，多糖提取濃度達到平衡濃度一半所需時間隨著溫度的升高而減小。同一溫度下，多糖提取濃度達到平衡濃度一半所需時間隨著功率的升高而減小。達到平衡濃度一半所需時間反映了提取的效率，達到平衡濃度一半所需時間越短提取速率越快。所以溫度升高、超聲功率增大能夠加快提取速率。

2.5 平均擴散系數的求解

整個提取過程的平均擴散系數可以通過提取速率常數k來計算。提取速率常數是與平均擴散系數(D)、物料形狀和大小相關聯的[22]。滿足k=π2D/R2。壺瓶碎米薺多糖為球形顆粒,R=0.077 mm。由k=π2D/R2可知，擴散系數D可以根據與速率常數、顆粒半徑之間的關系函數D=kR2/π2得到。

超聲提取時，整個體系的擴散系數不僅是多糖分子在水中的擴散系數Dw，還包含超聲引起的擴散系數Dc。Dw主要是溫度作用下的擴散，Dc為超聲引起的渦流擴散系數[23]。超聲作用下，溫度引起的擴散作用遠小于超聲引起的擴散。所以忽略Dw，D=Dc[24]。多糖提取過程作D與溫度關系圖(圖8)；作D與超聲功率的關系圖(圖9)。根據得到的回歸方程可分別計算出2種不同提取方法下的有效擴散系數。

圖8 平均擴散系數與溫度的關系圖Fig.8 Relationship between average diffusion coefficient and temperature

由圖8得到在超聲功率為240 W時平均擴散系數的擬合方程為：D=9.59×10-7e0.009 9T,R2=0.937 9。由圖9可以得出，在溫度為353 K時平均擴散系數的擬合方程為：D=1.59×10-5e0.003P,R2=0.919 6。當溫度一定，功率不同時，平均擴散系數隨著功率增大而增大。當功率固定，溫度不同時，平均擴散系數隨著溫度增大而增大。

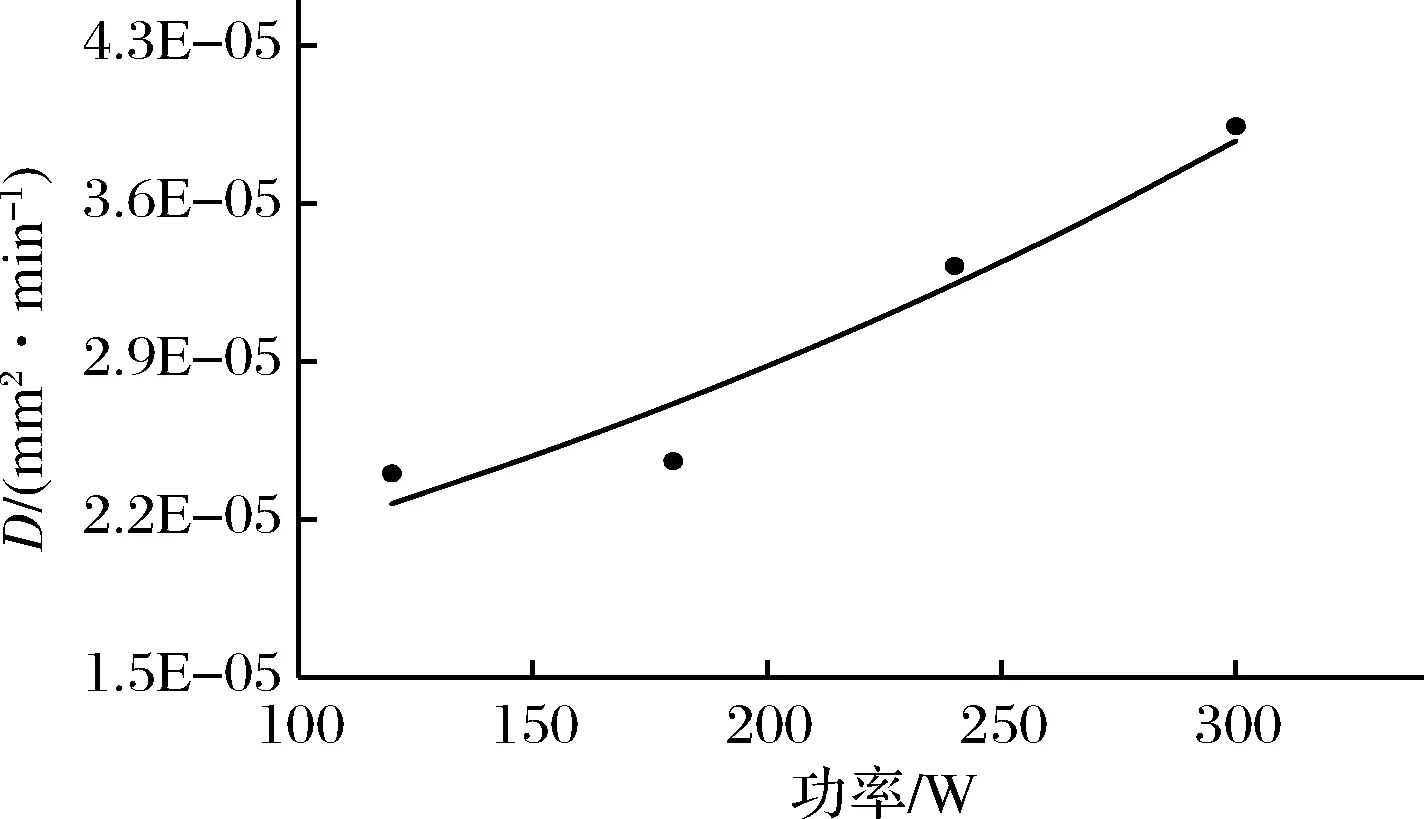
圖9 平均擴散系數與功率的關系圖Fig.9 Relationship between average diffusion coefficient and work and power

3 結論

結合 Fick 第二定律，建立了超聲提取壺瓶碎米薺多糖質量的動力學模型，建立的動力學模型展現出了提取壺瓶碎米薺多糖質量濃度與壺瓶碎米薺顆粒半徑、時間、擴散系數之間的關系。在此基礎上，以壺瓶碎米薺粉末為原料，在不同溫度和超聲功率下提取多糖，檢測得到不同提取條件下的多糖的質量濃度。測得的多糖濃度與動力學模型方程結合，得到壺瓶碎米薺多糖提取過程中的一般方程、指數方程和相關參數。因為超聲波處理可能導致顆粒微觀結構的破壞[25]，試驗假定壺瓶碎米薺顆粒在提取過程中半徑不變，且超聲儀器的控溫系統不夠穩定等原因，會影響實驗數據結果，降低相關方程的相關性，導致試驗的相關系數未均達到0.95，但基本都達到了0.9，所以試驗測得數據與動力學模型計算值具有一定的吻合性，求得的動力學參數可以為壺瓶碎米薺多糖提取工藝的優化提供一定的理論基礎。