雙極型晶體管總劑量效應的統計特性*

李順 宋宇 周航 代剛 張健

1) (中國工程物理研究院微系統與太赫茲研究中心, 成都 610200)

2) (內江師范學院物理與電子信息工程學院, 內江 641112)

3) (電子科技大學電子科學與工程學院, 成都 611731)

4) (中國工程物理研究院電子工程研究所, 綿陽 621000)

雙極型晶體管的總電離劑量輻照效應主要體現在基極電流(IB)的退化, 其作用機理是電離輻射在SiO2中及Si/SiO2界面作用導致的氧化物陷阱電荷面密度(Not)和界面陷阱電荷面密度(Nit)的增長.本文基于定制設計的柵控橫向PNP晶體管, 開展了大樣本、多劑量點的電離總劑量效應實驗, 獲得了雙極型晶體管IB, Not, Nit的分散性及其隨總劑量變化的統計特性, 初步建立了晶體管損傷分散性與Not分散性的關聯.該研究成果可以有效支撐雙極型電路輻射可靠性的機理研究與定量評估.

1 引 言

由于半導體器件制造過程中存在材料的不一致性和工藝的波動性, 即便是同一廠商、同一批次的半導體器件, 其電學參數也具有樣本間分散性(sample-to-sample variability).這種分散性可以通過統計特性描述.半導體器件的分散性可分為自身因素導致的本征分散性 (intrinsic variability)和外部因素導致的外在分散性 (extrinsic variability)[1].自身因素是由器件之間原子級差異造成的, 主要來源包括摻雜分布、邊緣粗糙度和膜厚變化.外在因素的主要來源包括工藝波動和不同位置、不同損耗、不同使用條件引起的器件性能波動等[1].

運算放大器等硅基雙極型器件是電子產品中常用的關鍵元器件.在衛星等空間應用條件下, 由于受到電離輻射, 會產生總電離劑量(total ionization dose, TID)效應.由于上述自身因素和外部因素的影響, 雙極器件的總劑量效應也會呈現一定的分散性.文獻[2?10]研究了不同制造商、不同批次、不同晶圓、不同芯片、不同晶體管導致的雙極器件總劑量效應的分散性.文獻[3]對總劑量輻照下電壓比較器LM111、LM211和LM311的輸入偏置電流的分散性進行了研究, 發現不同制造廠家的效應差距可達100倍之多.文獻[5]研究了108 A運算放大器及其單管的批次間、晶圓間、芯片間分散性, 發現可以通過測試更低層級器件獲得運算放大器的良率.文獻[6, 7]對國家半導體(National Semiconductor)公司多種型號放大器的總劑量效應分散性進行了研究, 發現器件間分散性、晶圓間分散性顯著大于溝道間分散性.文獻[8]研究了多種放大器(LM111/LM124/OP-27/OP-484/RH1014/RH1056)批次間分散性受中子輻射的影響.我們最近的研究表明, NPN和PNP型雙極器件的中子-伽馬輻照協同效應(irradiation synergistic effect)具有顯著的樣本間分散性, 該分散性支撐實現了協同效應對初始位移損傷依賴性的自洽建模[11,12].雙極型器件的基本組成單元是雙極型晶體管, 其輻射分散性是器件統計特性的基礎, 但當前研究尚未深入到晶體管層次, 對晶體管總劑量效應的統計特性及其來源缺乏清晰的認識.

本文基于雙極晶體管總劑量效應的微觀機理,設計并制備了用于輻射敏感參數測試的柵控橫向PNP晶體管(gated lateral PNP, GLPNP), 開展了大樣本晶體管的多劑量點總劑量輻照效應實驗和測試, 研究了晶體管基極電流(base current,IB)、氧化物陷阱電荷面密度(Not)、界面態陷阱電荷面密度(Nit)在總劑量輻射下的分散性及變化.研究獲得了晶體管及材料層級的總劑量效應統計特性,分析了總劑量效應分散性的晶體管-材料關聯, 從電離缺陷的微觀角度解釋了晶體管總劑量效應分散性的物理起源.

2 實驗設計

雙極型晶體管總劑量效應主要體現在基極電流(IB)的退化, 其微觀作用機理為電離輻射在SiO2材料中和Si/SiO2界面上作用積累的氧化物陷阱電荷面密度和界面態陷阱電荷面密度的變化[13,14].為了研究晶體管IB總劑量效應分散性的微觀起源,我們設計并制備了GLPNP晶體管結構.GLPNP的結構和參數如圖1和表1所示.其主要結構為橫向PNP晶體管, 并在基區上覆蓋一個金屬電極, 從而可以施加柵極電壓.通過改變柵極電壓調節基區表面勢, 可以使得表面實現反型、積累、耗盡等狀態, 從而實現P型金屬氧化物半導體場效應晶體管(PMOSFET)的柵控特性.通過該柵控結構的柵掃描(gate sweep curve, GS)曲線和亞閾值掃描(sub-threshold sweep, DS)曲線的測試可獲得與IB對應的Not和Nit的大小[15?17], 從而探索晶體管基極電流分散性和缺陷面密度分散性的關聯.

圖1 GLPNP器件的結構示意圖Fig.1.Structure of the GLPNP transistor.

表1 GLPNP的結構尺寸參數Table 1.Structure parameters of the GLPNP transistor.

選取同一批次的GLPNP共40只, 在0.6 krad(Si), 2.6 krad(Si), 4.0 krad(Si), 7.4 krad(Si), 10.8 krad(Si)等5個總劑量點進行序貫電離輻射實驗.輻射源為北京大學的60Co裝置, 中心劑量率大于300 rad(Si)/s.為了保證40個樣本試驗劑量率的均勻性, 將每4只單管封裝在一起(雙排直插), 并將10個封裝疊成三排嵌入輻照板內, 在離輻射源較遠的位置進行輻照, 劑量率為3.4 rad(Si)/s.此時, 40只單管幾乎分布在以輻射源為中心的圓弧上, 從而保證劑量率的均勻性.實驗過程中器件所有管腳空載, 輻照到上述劑量點后進行離線測試.通過測試Gummel特性曲線(即基極、集電極零偏, 發射結施加正偏掃描電壓)獲得GLPNP基極電流大小隨基區-發射極電壓(VBE)的變化規律,讀取VBE= 0.6 V時基極電流數值, 記錄為IB.輻射感生缺陷面密度Not與Nit的提取從GS和DS曲線上獲得.GS曲線的測試方法為固定發射結電壓為0.5 V, 集電極與基極均零偏, 柵極電壓從5 V掃描到–40 V.此時, GS曲線上峰值電流對應的柵極電壓為平帶電壓, 該電壓在輻照前后的變化即為Not導致的柵壓變化[17].由于在輻照過程中同時釋放和湮滅質子, 質子處于準平衡狀態, 其濃度在該測試結果中的比重很小, 可以忽略.DS曲線即PMOSFET對應的轉移特性曲線.固定發射結電壓1 V, 其余電極零偏, 柵壓從5 V掃描到–40 V,獲得轉移特性曲線.從各個劑量點的轉移特性曲線上提取閾值電壓的變化值, 該差值即為Not和Nit共同導致的閾值電壓漂移總量[15,16].該值減去前面求得的Not導致的平帶電壓漂移量, 可獲得Nit導致的閾值電壓漂移量, 即實現Not與Nit的分離測試.輻照、測試的實驗溫度均為室溫.包含跳線在內, 完成一只器件的以上所有測試大約需要60 s,完成所有40只器件的所有測試的時間在一個小時以內.這種測試符合GJB548B/MIL-STD-883G關于總劑量輻照實驗的要求.另外, 李興冀等[18]的研究結果表明128天的室溫退火也僅造成很小的Not退火, 且不同于氧化物陷阱電荷, 界面陷阱在室溫下不退火[19].因此, 不同樣本間的不同測試時間間隔不會導致顯著的樣本間分散性.

3 實驗結果與理論分析

3.1 基極電流的統計特性分析

實驗獲得的不同總劑量條件下40只GLPNP樣本的基極電流的統計分布見圖2.可以看到, 基極電流的分布是不對稱的.當總劑量較小時, 較多的樣本分布在中值的右側; 總劑量較大時, 較多的樣本分布在中值的左側.對于4.0 krad(Si)的總劑量, 分布基本對稱.研究發現這些分布均滿足對數正態分布(lognormal distribution)[20], 其概率密度函數(probability distribution function)為

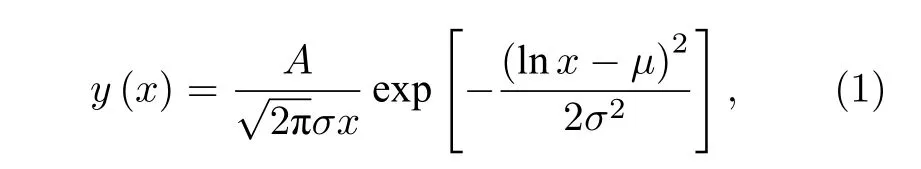
其中,μ為中位數,σ為標準差,A為歸一化常數.擬合曲線如圖2中紅線所示, 可見擬合度較高.擬合獲得的μ和σ分別畫為圖3(a)和圖3(b)中的黑點.我們也分析了輻照前基極電流的統計特性, 其大小滿足高斯正態分布.

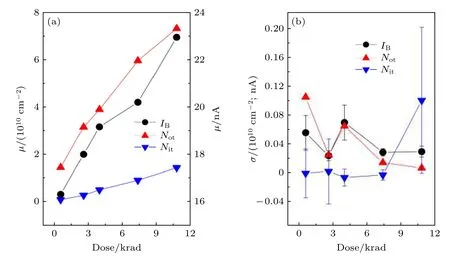
圖3 分布參數 (a) μ 和 (b) σ 隨總劑量的變化規律Fig.3.Statistical parameters (a) μ and (b) σ as a function of the total dose.

由圖2可以看出, 不同總劑量條件下基極電流均滿足對數正態分布, 但分布的具體參數隨總劑量的增大發生了變化.其中分布中位數μ隨總劑量增大而單調增大, 初始階段呈現亞線性增長趨勢, 分布標準差σ隨總劑量增大表現出振蕩行為.

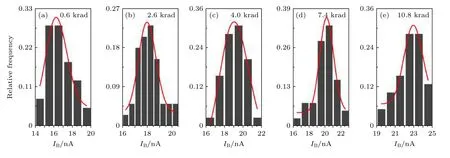
圖2 不同總劑量條件下GLPNP基極電流的分布特性Fig.2.Statistical characteristics of the base current of GLPNP under different total doses as indicated in each subfigure.

3.2 基極電流分散性的起源分析

以往的研究表明, 電離輻射造成的晶體管基極電流有兩個分量[21,22], 一個是空間電荷區表面的復合電流, 一個是中性基區表面的復合電流.前者起源于發射極-基極(EB)結空間電荷區表面Nit對載流子的復合作用, 表達式為[21,23]

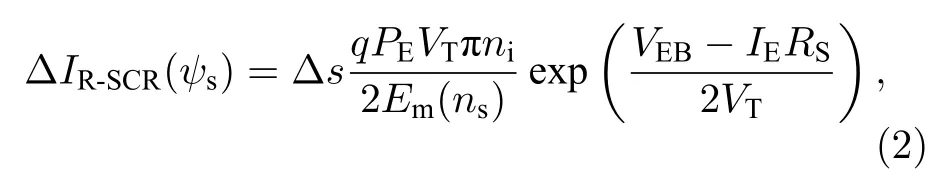
后者起源于中性基區表面的載流子復合作用, 其表達式為[22,23]

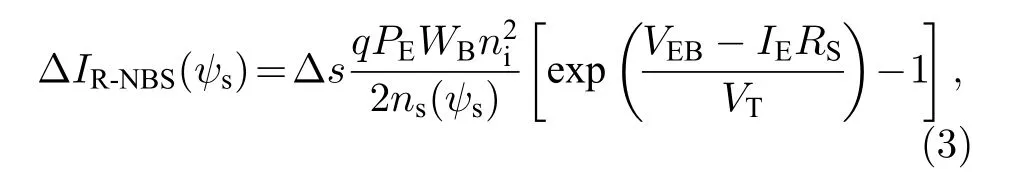
其中, ?s(s–1)是Nit(cm–2)造成的表面復合速率[24,25];PE(cm)是發射極周長;Em(V/cm)是E-B結空間電荷區的最大電場, 大小由表面電荷濃度ns(cm–2)決定;ns的大小由Not(cm–2)唯一決定[22];WB(cm)是發射極到集電極之間的寬度.電離誘導基極復合電流是表面電勢ψs的函數[23].

從該模型可以看出, GLPNP基極電流的總劑量效應分散性可以起源于多種因素.電離缺陷方面,Not(決定ns和Em)和Nit(決定 ?s)可能由于氧化物和界面中缺陷前驅體初始濃度及分布的不同、氫分子濃度的不同[26], 表現出顯著的分散性,從而造成基極電流的統計特性; 器件結構和摻雜方面, 由于制備工藝, 基區摻雜濃度、基區寬度等可能存在樣本間分散性, 也造成基極電流的樣本間分散性和統計特性.本工作重點關注電離缺陷的影響, 通過GLPNP測試獲得Not和Nit的統計特性,從而探索它們對IB統計特性的貢獻.

3.3 電離缺陷的統計特性及其與基極電流的關聯分析

與圖2中IB對應的Not,Nit分布如圖4和圖5所示.圖4和圖5中的(a)—(e)分別為不同總劑量條件下40只晶體管的實驗結果, 注意圖5中Nit的單位是109cm–2, 不同于圖4 中Not的單位(1010cm–2).研究發現,Not和Nit兩類缺陷的面密度也滿足對數正態分布, 隨總劑量增大,Not,Nit的對數正態分布形貌未發生變化, 但分布參數發生變化.為方便對比, 刻畫分布的中位數μ和標準差σ也畫在圖3中, 見紅點(Not)和藍點(Nit).輻照前的Nit滿足高斯正態分布, 由于所用樣品電容過小,無法獲得輻照前Not的數值.

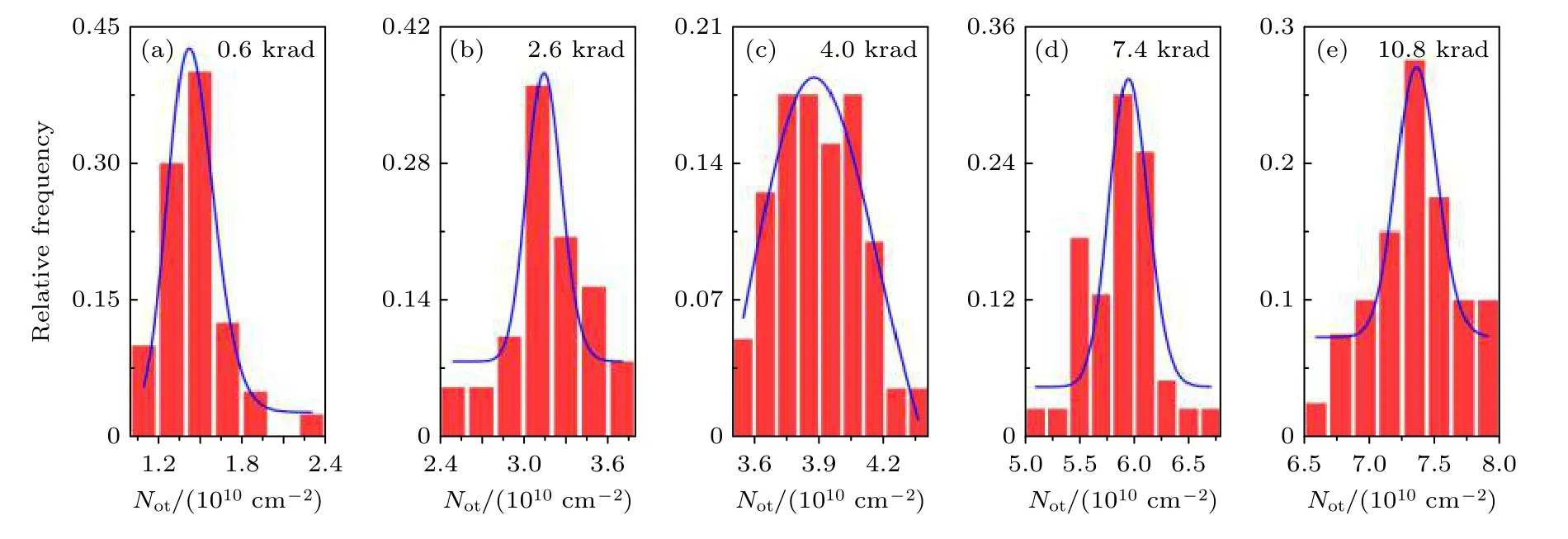
圖4 不同總劑量條件下Not的分布特性Fig.4.Statistical characteristics of Not under different total dose irradiations.

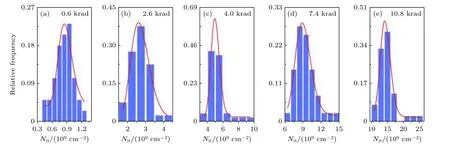
圖5 不同總劑量條件下Nit分布特性Fig.5.Statistical characteristics of Nit under different total dose irradiations.

從圖3可以觀察到幾個重要信息.第一,Not比Nit大若干倍, 表明該劑量率下GLPNP中的電離缺陷以氧化物陷阱電荷為主, 氧化物陷阱電荷向界面陷阱電荷的轉化較少.當劑量率下降時,Nit所占比重會逐漸增大, 甚至超過Not的比重[27].第二,兩類缺陷面密度的統計中位數μ均隨總劑量增大而單調增大.不同的是,Not中位數的增長是亞線性的,Nit中位數的增長表現出輕微的超線性.兩種不同的非線性起源于非晶二氧化硅中Not產生與Not-Nit轉化兩種機制的相互作用[27].該作用造成一個非單調的干涉項.在Not中該項為正, 導致Not呈現出對總劑量的亞線性依賴; 在Nit中該項為負,使得Nit表現出對總劑量的超線性依賴[27].第三,兩類缺陷的統計標準差σ隨總劑量變化呈現非常不同的特性.Not的統計標準差隨總劑量增大而振蕩, 而Nit的統計標準差隨總劑量增大幾乎單調增大.

可以通過對比IB,Not,Nit的統計特性來分析晶體管基極電流分散性與氧化物電離缺陷分散性之間的關聯.在圖3中可以清楚地看到, 統計中位數方面,IB對總劑量的亞線性依賴與Not的依賴性相同, 而與Nit的超線性依賴不相同.同時, 統計標準差方面,IB隨總劑量振蕩的行為與Not的行為非常相似, 而非常不同于Nit的單調增長行為.這些強烈關聯的行為意味著在本文研究的對象和劑量率條件下,IB主要起源于Not的貢獻, 因而IB的分散性主要由Not的分散性決定.Not的大小主要由缺陷前驅體的濃度決定, 因而可以通過控制缺陷前驅體濃度的分散性來保證IB的樣本間均一性, 從而生產高質量的雙極器件.

4 結 論

本文對雙極型晶體管總劑量效應的統計特性進行了研究, 基于同批次、多樣本定制柵控晶體管的多總劑量點伽馬輻照實驗獲得了器件基極電流大小、氧化物陷阱電荷面密度、界面陷阱電荷面密度的對數正態分布特性, 以及統計中位數和標準差隨總劑量增長的變化規律.研究發現, 基極電流總劑量效應的統計特性與氧化物陷阱電荷的統計特性存在很強的相似性和關聯, 而與界面陷阱電荷的統計特性非常不同, 意味著在本文研究的對象和劑量率條件下,IB主要起源于Not的貢獻, 因而IB的分散性主要由Not的分散性決定.該研究成果將微電子器件輻射分散性的研究深入到晶體管和材料層次, 可以有效支撐基于物理模型的輻射可靠性機理研究與定量評估.